12 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 29

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 29

3250 lượt thi
12 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

1, a) Tìm x biết $4 x + 2 = 0$

Xem đáp án

1, $a) 4 x + 2 = 0 \Leftrightarrow 4 x = - 2 \Leftrightarrow x = - \frac{1}{2}$

Vậy $S = \{- \frac{1}{2}\}$

Câu 2:

b, Rút gọn: $A = (\sqrt{5} - 3) (\sqrt{5} + 3) + 6$

Xem đáp án

$b) A = (\sqrt{5} - 3) (\sqrt{5} + 3) + 6 = 5 - 9 + 6 = 2$

Câu 3:

2) Cho đường thẳng $(d) : y = 2 x - 2$

a) Vẽ đường thẳng (d) trong hệ trục tọa độ Oxy

Xem đáp án

2, a) Học sinh tự vẽ

Câu 4:

b) Tìm m để đường thẳng $(d') : y = (m - 1) x + 2 m$ song song với đường thẳng (d)

Xem đáp án

b) Để $(d') y = (m - 1) x + 2 m$ song song với (d) $\Rightarrow \{\begin{cases} m - 1 = 2 \\ 2 m \neq - 2 \end{cases} \Leftrightarrow \{\begin{cases} m = 3 \\ m \neq - 1 \end{cases} \Leftrightarrow m = 3$

Câu 5:

Cho phương trình $2 x^{2} - 6 x + 2 m - 5 = 0$ (m là tham số)

1,Giải phương trình với m=2

Xem đáp án

1, Khi m=2 ta có phương trình: $2 x^{2} - 6 x - 1 = 0$

$Δ' = {(- 3)}^{2} - 2. (- 1) = 11$ $\Rightarrow$ phương trình có 2 nghiệm $[\begin{array}{l} x_{1} = \frac{3 + \sqrt{11}}{2} \\ x_{2} = \frac{3 - \sqrt{11}}{2} \end{array}$

Câu 6:

2,Tìm m để phương trình có hai nghiệm $x_{1}, x_{2}$ thỏa mãn: $\frac{1}{x_{1}} + \frac{1}{x_{2}} = 6$

Xem đáp án

2, $2 x^{2} - 6 x + 2 m - 5 = 0 (1)$

$Δ' = {(- 3)}^{2} - 2 (2 m - 5) = 9 - 4 m + 10 = 19 - 4 m$

Để phương trình có nghiệm $\Leftrightarrow 19 - 4 m \geq 0 \Leftrightarrow m \leq \frac{19}{4}$

Khi đó, áp dụng hệ thức Vi-et $\Rightarrow \{\begin{cases} x_{1} + x_{2} = 3 \\ x_{1} x_{2} = \frac{2 m - 5}{2} \end{cases}$

Ta có: $\frac{1}{x_{1}} + \frac{1}{x_{2}} = 6$

$\begin{array}{l} \Leftrightarrow \frac{x_{1} + x_{2}}{x_{1} x_{2}} = 6 \Leftrightarrow x_{1} + x_{2} = 6 x_{1} x_{2} \\ \Leftrightarrow 3 = 6. \frac{2 m - 5}{2} \Leftrightarrow 3 = 3 (2 m - 5) \Leftrightarrow m = 3 \end{array}$

Câu 7:

Bác Bình dự định trồng 300 cây cam theo nguyên tắc trồng thành các hàng, mỗi hàng có số cây bằng nhau. Nhưng khi thực hiện bác Bình đã trồng thêm 2 hàng, mỗi hàng thêm 3 cây so với dự kiến ban đầu nên đã trồng được tất cả 391 cây. Tính số cây trên một hàng mà bác Bình dự kiến trồng ban đầu

Xem đáp án

Gọi x là số cây trên 1 hàng $(x \in ℕ *, x < 300)$ $\Rightarrow$ Số hàng là: $\frac{300}{x}$

Theo đề ta có phương trình:

$\begin{array}{l} (\frac{300}{x} + 2) (x + 3) = 391 \\ \Leftrightarrow 300 + 2 x + \frac{900}{x} + 6 = 391 \\ \Leftrightarrow 2 x^{2} - 85 x + 900 = 0 \Leftrightarrow [\begin{array}{l} x = \frac{45}{2} (k t m) \\ x = 20 (t m) \end{array} \end{array}$

Vậy dự định bác Bình trồng 20 cây/ 1 hàng

Câu 8:

Cho đường tròn (O) đường kính AB điểm I nằm giữa hai điểm A và O (I khác A và O). Kẻ đường thẳng vuông góc với AB tại I, đường thẳng này cắt đường tròn (O) tại M và N. Gọi S là giao điểm của hai đường thẳng BM và AN, qua S kẻ đường thẳng song song với MN đường thẳng này cắt các đường thẳng AB và AM lần lượt tại K và H

a,Chứng minh rằng tứ giác SKAM nội tiếp

Xem đáp án

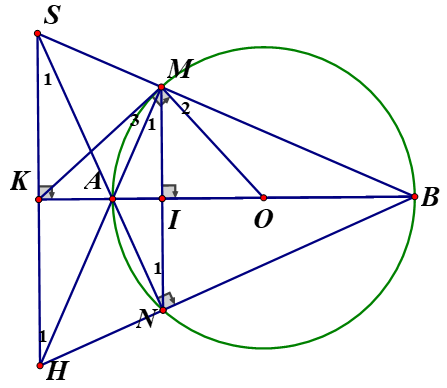
Cho đường tròn (O) đường kính AB điểm I nằm giữa hai điểm A và O (I khác A và O) (ảnh 1)

a, Vì $M N / / S H$ mà $B I ⊥ M N \Rightarrow B K ⊥ S H \Rightarrow \hat{S K A} = 90^{0}$

$\hat{A M B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn ) $\Rightarrow \hat{S M A} = 90^{0}$

Tứ giác SKAM có $\hat{K} + \hat{M} = 90^{0} + 90^{0} = 180^{0} \Rightarrow S K A M$ là tứ giác nội tiếp.

Câu 9:

b, Chứng minh rằng SA. SN =SB. SM

Xem đáp án

b, Ta có: $\hat{S N B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

Xét $Δ S A M$ và $Δ S B N$ có $\hat{S}$ chung; $\hat{M} = \hat{N} = 90^{0}$

$\Rightarrow Δ S A M ~ Δ S B N (g . g) \Rightarrow \frac{S A}{S M} = \frac{S B}{S N} \Rightarrow S A . S N = S B . S N$

Câu 10:

c,Chứng mnh rằng KM là tiếp tuyến của đường tròn (O)

Xem đáp án

c,Ta có: $A I ⊥ M N$ và I là trung điểm MN (đường kính – dây cung)

$\Rightarrow Δ A M N$ cân tại A $\Rightarrow \hat{N_{1}} = \hat{M_{1}} (1)$

Mà $\hat{N_{1}} = \hat{S_{1}}$ (so le trong) (2) , $\hat{S_{1}} = \hat{H_{1}} (= \hat{M_{1}} = \hat{N_{1}} (s o .. l e ... t r o n g)) (3)$

$\hat{H_{1}} = \hat{B_{1}}$ (cùng phụ $\hat{K S M}) (4)$ $\hat{B_{1}} = \hat{M_{2}} (Δ M O B$ cân) (5)

Từ (1),(2), (3), (4), (5) $\Rightarrow \hat{M_{1}} = \hat{M_{2}}$

Lại có $s d \overset{⏜}{A M} = s d \overset{⏜}{A N} \Rightarrow \hat{M_{1}} = \hat{M_{3}}$ (hai góc cùng chắn hai cung bằng nhau)

$\Rightarrow \hat{M_{2}} = \hat{M_{3}} \Rightarrow \hat{M_{2}} + \hat{O M A} = \hat{M_{3}} + \hat{O M A} \Rightarrow \hat{O M K} = 90^{0}$

Mà $M \in (O) \Rightarrow K M$ là tiếp tuyến của (O)

Câu 11:

d,Chứng minh rằng 3 điểm H,N, B thẳng hàng

Xem đáp án

d, Ta có: $\hat{A N B} = 90^{0} (c m t) \Rightarrow A N ⊥ N B$ hay $S N ⊥ N B (6)$

Lại có: $\hat{A M B} = 90^{0} \Rightarrow \hat{H M S} = 90^{0}$ (kề bù)

$\Rightarrow Δ S B H$ có $B K, H M$ là hai đường cao $\Rightarrow A$ là trực tâm $\Rightarrow S N ⊥ H B (7)$

Từ (6) , (7) $\Rightarrow H, N, B$ thẳng hàng

Câu 12:

Cho hai số thực dương a,b thỏa mãn a +b =4ab

Chứng minh rằng: $\frac{a}{4 b^{2} + 1} + \frac{b}{4 a^{2} + 1} \geq \frac{1}{2}$

Xem đáp án

Ta có: $a + b = 4 a b \Rightarrow \frac{1}{a} + \frac{1}{b} = 4 \geq \frac{4}{a + b}$

$\Rightarrow a + b \geq 1 \Rightarrow {(a + b)}^{2} \geq a + b$

Ta có:

$\frac{a}{4 b^{2} + 1} = \frac{a^{2}}{4 a b^{2} + a} = \frac{a^{2}}{b^{2} + a b + a}$

Tương tự: $\frac{b}{4 a^{2} + 1} = \frac{b^{2}}{a^{2} + a b + b}$

$\Rightarrow V T \geq \frac{{(a + b)}^{2}}{{(a + b)}^{2} + (a + b)} \geq \frac{{(a + b)}^{2}}{2 {(a + b)}^{2}} \geq \frac{1}{2}$

Dấu "=" xảy ra $\Leftrightarrow a = b = \frac{1}{2}$

Bắt đầu thi ngay