Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:
Giải bởi Vietjack
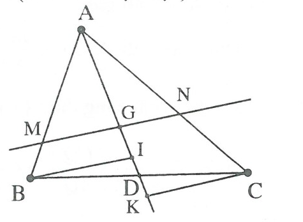
* Tìm cách giải. Để tạo ra tỉ số chúng ta cần vận dụng định lý Ta-let, mà hình vẽ chưa có yếu tố song song do vậy chúng ta cần kẻ thêm yếu tố song song. Kẻ đường thẳng song song với MN từ B và C vừa khai thác được yếu tố trọng tâm, vừa tạo ra được tỉ số yêu cầu.
* Trình bày lời giải
Trường hợp 1. Nếu MN // BC, thì lời giải giản đơn (dành cho bạn đọc).
Trường hợp 2. Xét MN không song song với BC.
Xét
hay suy ra
Nhận xét. Từ kết quả (1), chúng ta thấy rằng bởi G là trọng tâm nên . Vậy nếu G không phải là trọng tâm thì ta có bài toán sau:
- Một đường bất kỳ cắt cạnh AB, AC và đường trung tuyến AD của tam giác ABC lần lượt tại M, N và G. Chứng minh rằng:
- Nếu thay yếu tố trung tuyến bằng hình bình hành, ta có bài toán sau: Cho hình bình hành ABCD. Một đường thẳng bất kỳ cắt AB, AD và AC lần lượt tại M, N và G. Chứng minh rằng:
Cho tam giác ABC nhọn có AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho . Chứng minh rằng: .
Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:
Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:
Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:
