Giải bởi Vietjack
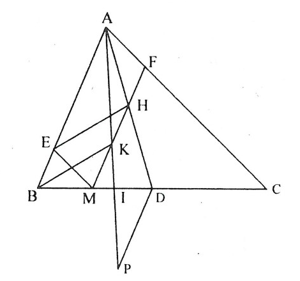
Qua D kẻ đường thẳng song song với AB, cắt tia AI tại P. Áp dụng định lý Ta-let, cho các đoạn thẳng song song ta có:
(1).
(2).
và (3).
Từ (1), (2) và (3) suy ra:
. Vậy
Cho tam giác ABC nhọn có AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho . Chứng minh rằng: .
Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:
Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:
Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:
Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:
