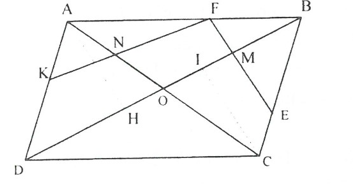
Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:
Giải bởi Vietjack
* Tìm cách giải.
Với phân tích và suy luận như câu a, ví dụ 4 thì câu a, ví dụ này không quá khó.
Tương tự câu a, chúng ta có kết quả: và suy ra để liên kết được BE + AK với nhau, mà với suy luận trên thì BE, AK cùng nằm ở mẫu số, do đó chúng ta liên tưởng tới bất đẳng thức đại số sẽ cho chúng ta yêu cầu. Với suy luận đó, chúng ta có lời giải sau:
* Trình bày lời giải
Tương tự ta có:
(1)
Áp dụng bất đẳng thức (với )
Ta có: (2)
Từ (1) và (2) suy ra:
Mà
Cho tam giác ABC nhọn có AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho . Chứng minh rằng: .
Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:
Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng:
Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng:
