Giải bởi Vietjack
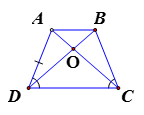
Xét hai tam giác BDC và ACD có: cạnh DC chung; và AD = BC (tính chất hình thang cân)
(c-g-c)
cân tại O => OD = OC
Chứng minh tương tự ta có OB = OC.
Cho tam giác ABC cân tại A . Đường thẳng song song với BC cắt hai cạnh AB, AC lần lượt tại M, N. Chứng minh BCNM là hình thang cân.
Cho tam giác ABC cân tại A . Trên tia đối của tia AB lấy điểm D; trên tia đối của tia AC lấy điểm E sao cho AD = AE. Tứ giác BCDE là hình gì? Vì sao?
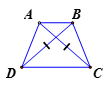
Trong các hình vẽ sau, hình nào là hình thang cân. Giải thích.
Cho tam giác đều ABC, điểm M nằm trong tam giác đó. Qua M, kẻ các đường thẳng song song với AC cắt BC ở D, kẻ đường thẳng song song với AB cắt AC ở E, kẻ đường thẳng song song với BC cắt AB ở F. Chứng minh rằng:
a)
Chứng minh rằng trong một hình thang cân, đường chéo luôn lớn hơn đường trung bình.
