Cho tam giác ABC cân tại A . Trên tia đối của tia AB lấy điểm D; trên tia đối của tia AC lấy điểm E sao cho AD = AE. Tứ giác BCDE là hình gì? Vì sao?
Giải bởi Vietjack
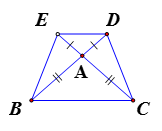
Theo giá thiết ta có các tam giác ABC và ADE là các tam giác cân nên và
Mặt khác (đối đỉnh) nên
Mà hai góc này ở vị trí so le trong nên DE // BC
=> BCDE là hình thang
Lại có EC = EA + AC = DA + AB = DB nên BCDE là hình thang cân.
Cho tam giác ABC cân tại A . Đường thẳng song song với BC cắt hai cạnh AB, AC lần lượt tại M, N. Chứng minh BCNM là hình thang cân.
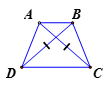
Trong các hình vẽ sau, hình nào là hình thang cân. Giải thích.
Cho tam giác đều ABC, điểm M nằm trong tam giác đó. Qua M, kẻ các đường thẳng song song với AC cắt BC ở D, kẻ đường thẳng song song với AB cắt AC ở E, kẻ đường thẳng song song với BC cắt AB ở F. Chứng minh rằng:
a)
Chứng minh rằng trong một hình thang cân, đường chéo luôn lớn hơn đường trung bình.
