Trong buổi lễ kỉ niệm ngày thành lập Đoàn Thanh niên cộng sản Hồ Chí Minh 26 – 3, bí thư Đoàn trường cần chọn 3 tiết mục từ 7 tiết mục hát và 3 tiết mục từ 6 tiết mục múa rồi xếp thứ tự biểu diễn. Hỏi có bao nhiêu cách chọn và xếp thứ tự sao cho các tiết mục hát và múa xen kẽ nhau?
Giải bởi Vietjack
Giả sử các tiết mục được biểu diễn đánh số thứ tự từ 1 đến 6. Vì số lượng tiết mục hát và múa bằng nhau nên có hai trường hợp:
Trường hợp 1: Tiết mục hát diễn ra đầu tiên.
Khi đó, các tiết mục hát có số thứ tự là số lẻ, còn các tiết mục múa có số thứ tự là số chẵn. Như vậy, thứ tự của các tiết mục múa và hát được cố định, chỉ thay đổi thứ tự giữa các tiết mục múa hoặc giữa các tiết mục hát.
Chọn 3 tiết mục từ 7 tiết mục hát và xếp thứ tự có \(A_7^3 = 210\) (cách).
Chọn 3 tiết mục từ 6 tiết mục múa và xếp thứ tự có \(A_6^3 = 120\) (cách).
Khi đó, số cách chọn và xếp thứ tự các tiết mục văn nghệ trong trường hợp tiết mục hát diễn ra đầu tiên là: 210 . 120 = 25 200.
Trường hợp 2. Tiết mục múa diễn ra đầu tiên.
Tương tự, số cách chọn và xếp thứ tự các tiết mục văn nghệ trong trường hợp tiết mục múa diễn ra đầu tiên là: 120 . 210 = 25 200.
Vậy số cách chọn và xếp thứ tự các tiết mục văn nghệ sao cho các tiết mục hát và múa xen kẽ nhau là: 25 200 + 25 200 = 50 400.
Ở căn hộ chung cư nhà An người ta thường dùng các chữ số từ 0 đến 9 để thiết lập mật khẩu. Nhà An muốn thiết lập một mật khẩu gồm 4 chữ số khác nhau. Số cách thiết lập mật khẩu cho nhà An là
Nếu một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có a cách thực hiện, hành động thứ hai có b cách thực hiện (các cách thực hiện của hai hành động là khác nhau đôi một) thì số cách hoàn thành công việc đó là
Trong mặt phẳng tọa độ Oxy, cho A(1; 1) và B(5; – 2). Độ dài đoạn thẳng AB là
Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 - 7t\end{array} \right.\). Đường cao AH có phương trình 2x + 5y + 66 = 0. Viết phương trình đường trung trực của cạnh AB.
Số đo góc giữa hai vectơ \(\overrightarrow x = \left( {1;\,\, - 2} \right)\) và \[\overrightarrow y = \left( { - 2;\,\, - 6} \right)\] bằng
Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là 2 trong 8 điểm đó?
Các thành phố A; B; C; D được nối với nhau bởi các con đường như hình vẽ sau:
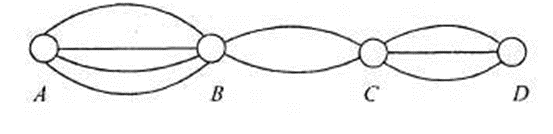
Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
Cho các điểm A(3; 7) và B(6; 1). Đường thẳng AB có phương trình là
Một lớp có 31 học sinh nam và 16 học sinh nữ. Có bao nhiêu cách chọn một học sinh làm lớp trưởng của lớp.
Thực hiện phép tính: \({\left( {\sqrt 7 + \sqrt 5 } \right)^5} - {\left( {\sqrt 7 - \sqrt 5 } \right)^5}\).
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Số các chỉnh hợp chập k của n phần tử trên là
Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là
Trong mặt phẳng tọa độ Oxy, cho M(2; – 1) và N(4; 1). Tọa độ vectơ \(\overrightarrow {NM} \) là
