 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Phân tích: Sự tồn tại của hàm số mũ và lượng giác trong cùng một nguyên hàm sẽ rất dễ gây cho người học sự nhầm lẫn, nếu ta sẽ không biết điểm dừng thì có thể sẽ bị lạc vào vòng luẩn quẩn. Ở đây, để tìm được kết quả thì ta phải từng phần hai lần như trong ví dụ 3. Tuy nhiên, với sơ đồ đường chéo thì sao? Khi nào sẽ dừng lại?
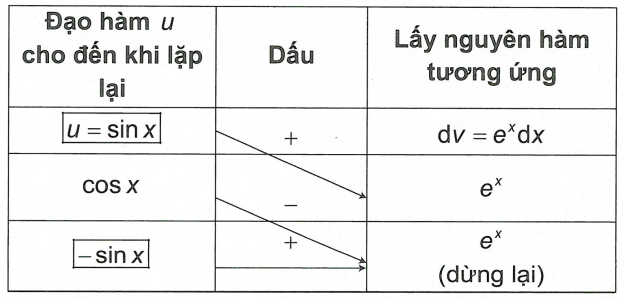
Khi đó, ta sẽ có thể kết luận \[I = {e^x}\sin x - {e^x}\cos x - \int {{e^x}\sin xdx} \].
Hay \[2I = {e^x}\sin x - {e^x}.\cos x\]. Vậy \[I = \frac{1}{2}{e^x}\left( {\sin x - \cos x} \right) + C\]
Chọn C.
Gọi \[F\left( x \right)\] là nguyên hàm của hàm số \[f\left( x \right) = \frac{{{{\cos }^5}x}}{{1 - \sin x}}\], với \[x \ne \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\] và thỏa mãn \[F\left( \pi \right) = \frac{3}{4}\]. Giá trị của \[F\left( { - \frac{\pi }{2}} \right)\] là: