Chuyên đề Toán 12 Bài 1: Nguyên hàm và phương pháp tìm nguyên hàm có đáp án
-
512 lượt thi
-
62 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
\[\int {\left( {{e^x} + x} \right)dx} = \int {{e^x}dx} + \int {xdx} = {e^x} + \frac{1}{2}{x^2} + C\].
Chọn B.
Câu 2:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\sqrt x dx} = \frac{2}{3}x\sqrt x + C\], với C là hằng số.
Nên các phương án A, B, D đều là nguyên hàm của hàm số \[y = \sqrt x \].
Chọn C.
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\begin{array}{l}\int {f\left( x \right)dx} = \int {\left( {3{x^2} + {3^x}} \right)dx} = \int {3{x^2}dx} + \int {{3^x}dx} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {x^3} + \frac{{{3^x}}}{{\ln 3}} + C\end{array}\]
Chọn B.Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\left( {5{x^4} + \frac{2}{{{x^2}}} - \sqrt[3]{x}} \right)dx} = {x^5} - \frac{1}{{{x^2}}} - \frac{3}{4}x\sqrt[3]{x} + C\]
Chọn A.
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\frac{{4{x^2} + \sqrt x - 6}}{x}dx} = \int {\left( {4x + \frac{1}{{\sqrt x }} - \frac{6}{x}} \right)dx} = 2{x^2} + 2\sqrt x - 6\ln \left| x \right| + C\]
Chọn C.
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\frac{{{2^x} - 1}}{{{e^x}}}dx} = \int {{{\left( {\frac{2}{e}} \right)}^x}dx} - \int {{e^{ - x}}dx} = \frac{{{2^x}}}{{{e^x}\left( {\ln 2 - 1} \right)}} + {e^{ - x}} + C\].
Chọn C.
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\begin{array}{l}\int {x{{\left( {x + 2} \right)}^{2019}}dx} = \int {\left[ {\left( {x + 2} \right) - 2} \right]{{\left( {x + 2} \right)}^{2019}}dx} \\ = \int {{{\left( {x + 2} \right)}^{2020}}dx} - 2\int {{{\left( {x + 2} \right)}^{2019}}dx} = \frac{{{{\left( {x + 2} \right)}^{2021}}}}{{2021}} - \frac{{{{\left( {x + 2} \right)}^{2020}}}}{{1010}} + C\end{array}\]
Chọn D.
Câu 8:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\frac{1}{{{e^{2x}} + 1}} = \frac{{\left( {{e^{2x}} + 1} \right) - {e^{2x}}}}{{{e^{2x}} + 1}} = 1 - \frac{{{e^{2x}}}}{{{e^{2x}} + 1}}\].
Do đó \[\int {\frac{1}{{{e^{2x}} + 1}}dx} = \int {\left( {1 - \frac{{{e^{2x}}}}{{{e^{2x}} + 1}}} \right)dx} = \int {dx} - \frac{1}{2}\int {\frac{{d\left( {{e^{2x}} + 1} \right)}}{{{e^{2x}} + 1}}} = x - \frac{1}{2}\ln \left( {{e^{2x}} + 1} \right) + C\]
Chọn B.
Câu 9:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\begin{array}{l}\int {\frac{1}{{\sqrt {x + 2} + \sqrt {x - 2} }}dx} = \int {\frac{{\sqrt {x + 2} - \sqrt {x - 2} }}{4}dx} \\ = \frac{1}{4}\left[ {\frac{2}{3}\left( {x + 2} \right)\sqrt {x + 2} - \frac{2}{3}\left( {x - 2} \right)\sqrt {x - 2} } \right] + C = \frac{1}{6}\left( {x + 2} \right)\sqrt {x + 2} - \frac{1}{6}\left( {x - 2} \right)\sqrt {x - 2} + C\end{array}\]
Chọn A.
Câu 10:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\frac{{5x - 13}}{{{x^2} - 5x + 6}} = \frac{{5x - 13}}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\]
Ta sẽ phân tích: \[5x - 13 = A\left( {x - 2} \right) + B\left( {x - 3} \right)\;\;\;\left( 1 \right)\]
Thế \[x = 2\] và \[x = 3\] lần lượt vào (1) ta có \[B = 3\] và \[A = 2\].
Khi đó \[\begin{array}{l}\int {\frac{{5x - 13}}{{{x^2} - 5x + 6}}dx} = \int {\frac{{2\left( {x - 2} \right) + 3\left( {x - 3} \right)}}{{\left( {x - 2} \right)\left( {x - 3} \right)}}dx} = \int {\frac{2}{{x - 3}}dx} + \int {\frac{3}{{x - 2}}dx} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 2\ln \left| {x - 3} \right| + 3\ln \left| {x - 2} \right| + C\end{array}\]
Chọn D.
Câu 11:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\frac{{1 - {x^4}}}{{{x^5} + x}}dx} = \int {\frac{{\left( {1 + {x^4}} \right) - 2{x^4}}}{{x\left( {{x^4} + 1} \right)}}dx} = \int {\frac{1}{x}dx} - \int {\frac{{2{x^3}}}{{{x^4} + 1}}dx} = \ln \left| x \right| - \frac{1}{2}\ln \left( {{x^4} + 1} \right) + C\]
Chọn C.
Câu 12:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\frac{{3{x^2} + 3x + 3}}{{{x^3} - 3x + 2}}dx} = \int {\frac{{3{x^2} + 3x + 3}}{{{{\left( {x - 1} \right)}^2}\left( {x + 2} \right)}}dx} \].
Ta phân tích \[3{x^2} + 3x + 3 = A{\left( {x - 1} \right)^2} + B\left( {x - 1} \right)\left( {x + 2} \right) + C\left( {x + 2} \right)\].
Ta có thể dùng các giá trị riêng, tính ngay \[A = 1,C = 3\] và \[B = 2\].
(thay \[x = - 2 \Rightarrow A = 1;\;x = 1 \Rightarrow C = 3\] và \[x = 0 \Rightarrow B = 2\]).
Khi đó \[\int {\frac{{3{x^2} + 3x + 3}}{{{{\left( {x - 1} \right)}^2}\left( {x + 2} \right)}}dx} = \int {\frac{1}{{x + 2}}dx} + 2\int {\frac{1}{{x - 1}}} dx + 3\int {\frac{1}{{{{\left( {x - 1} \right)}^2}}}dx} = \ln \left| {x + 2} \right| + 2\ln \left| {x - 1} \right| - \frac{3}{{x - 1}} + C\].
Chọn A.
Câu 13:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
\[f\left( x \right) = \int {f'\left( x \right)dx} = \int {\frac{2}{{2x - 1}}dx} = \ln \left| {2x - 1} \right| + C = \left\{ \begin{array}{l}\ln \left( {2x - 1} \right) + {C_1}\;khi\;x > \frac{1}{2}\\\ln \left( {1 - 2x} \right) + {C_2}\;khi\;x < \frac{1}{2}\end{array} \right.\]
Vì \[\left\{ \begin{array}{l}f\left( 0 \right) = 1\\f\left( 1 \right) = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{C_2} = 1\\{C_1} = 2\end{array} \right.\].
Suy ra \[f\left( x \right) = \left\{ \begin{array}{l}\ln \left( {2x - 1} \right) + 2\;khi\;x > \frac{1}{2}\\\ln \left( {1 - 2x} \right) + 1\;khi\;x < \frac{1}{2}\end{array} \right.\].
Do đó \[P = f\left( { - 1} \right) + f\left( 3 \right) = 3 + \ln 3 + \ln 5 = 3 + \ln 15\]
Chọn D.
Câu 14:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
\[f\left( x \right) = \int {f'\left( x \right)dx} = \int {\frac{2}{{{x^2} - 1}}dx} = \int {\left( {\frac{1}{{x - 1}} - \frac{1}{{x + 1}}} \right)dx} = \ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C\]
Hay \[f\left( x \right) = \ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C = \left\{ \begin{array}{l}\ln \left( {\frac{{x - 1}}{{x + 1}}} \right) + {C_1}\;khi\;x > 1\\\ln \frac{{1 - x}}{{1 + x}} + {C_2}\;khi\; - 1 < x < 1\\\ln \left( {\frac{{x - 1}}{{x + 1}}} \right) + {C_3}\;khi\;x < - 1\end{array} \right.\]
Theo bài ra, ta có: \[\left\{ \begin{array}{l}f\left( { - 3} \right) + f\left( 3 \right) = 2\ln 2\\f\left( { - \frac{1}{2}} \right) + f\left( {\frac{1}{2}} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{C_1} + {C_3} = 2\ln 2\\{C_2} = 0\end{array} \right.\]
Do đó \[f\left( { - 2} \right) + f\left( 0 \right) + f\left( 4 \right) = \ln 3 + {C_3} + {C_2} + \ln \frac{3}{5} + {C_1} = 2\ln 2 + 2\ln 3 - \ln 5\].
Chọn C.
Câu 15:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta viết: \[f\left( x \right) = \frac{1}{2}\left( {\cos 5x + \cos x} \right)\].
Khi đó: \[\int {f\left( x \right)dx} = \frac{{\sin 5x}}{{10}} + \frac{{\sin x}}{2} + C\]
Chọn A.Câu 16:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\left( {2\cos x - 3\cos 5x} \right)dx} = 2\sin x - \frac{3}{5}\sin 5x + C\]
Chọn C.
Câu 17:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\sin 5x\sin 2xdx} = \frac{1}{2}\int {\left( {\cos 3x - \cos 7x} \right)dx} = \frac{1}{6}\cos 3x - \frac{1}{{14}}\sin 7x + C\]
Chọn B.
Câu 18:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {4{{\cos }^2}xdx} = 2\int {\left( {1 + \cos 2x} \right)dx} = 2x + \sin 2x + C\].
Chọn D.
Câu 19:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\begin{array}{l}\int {{{\left( {1 + 2\sin x} \right)}^2}dx} = \int {\left( {1 + 4\sin x + 4{{\sin }^2}x} \right)dx} = \int {\left( {1 + 4\sin x + 4.\frac{{1 - \cos 2x}}{2}} \right)dx} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \int {\left( {3 + 4\sin x - 2\cos 2x} \right)dx} = 3x - 4\cos x - \sin 2x + C\end{array}\]
Chọn A.
Câu 20:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\begin{array}{l}\int {\left( {\sin x - \cos x} \right)\sin xdx} = \int {\left( {{{\sin }^2}x - \sin x\cos x} \right)dx} \\ = \int {\left( {\frac{{1 - \cos 2x}}{2} - \frac{{\sin 2x}}{2}} \right)dx} = \frac{1}{2}\left( {x - \frac{1}{2}\sin 2x + \frac{1}{2}\cos 2x} \right) + C\end{array}\]
Chọn B.
Câu 21:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\frac{1}{{{{\sin }^2}x{{\cos }^2}x}}dx} = \int {\frac{{{{\sin }^2}x + {{\cos }^2}x}}{{{{\sin }^2}x.{{\cos }^2}x}}dx} = \int {\left( {\frac{1}{{{{\cos }^2}x}} + \frac{1}{{{{\sin }^2}x}}} \right)dx} = \tan x - \cot x + C\].
Chọn B.
Câu 22:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {\frac{1}{{4{{\cos }^4}x - 4{{\cos }^2}x + 1}}dx} = \int {\frac{1}{{{{(2{{\cos }^2}x - 1)}^2}}}dx = } \int {\frac{1}{{{{\cos }^2}2x}}dx = } \frac{1}{2}\int {\frac{1}{{{{\cos }^2}2x}}d(2x) = \frac{{\tan 2x}}{2} + C} \]
Chọn D.
Câu 23:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {{{\cos }^3}xdx} = \frac{1}{4}\int {\left( {3\cos x + \cos 3x} \right)dx} = \frac{1}{4}\left( {3\sin x + \frac{1}{3}\sin 3x} \right) + C = \sin x - \frac{1}{3}{\sin ^3}x + C\]
Chọn C.
Câu 24:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Từ \[{\tan ^3}x = \tan x\left( {1 + {{\tan }^2}x} \right) - \tan x\]
Suy ra \[\int {{{\tan }^3}xdx} = \int {\tan xd\left( {\tan x} \right)} + \int {\frac{{d\left( {\cos x} \right)}}{{\cos x}}} = \frac{{{{\tan }^2}x}}{2} + \ln \left| {\cos x} \right| + C\].
Chọn A.
Câu 25:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[F\left( x \right) = \int {\sin 2x.\tan xdx} = \int {2\sin x.\cos x.\frac{{\sin x}}{{\cos x}}dx} = 2\int {{{\sin }^2}xdx} \].
Suy ra \[F\left( x \right) = \int {\left( {1 - \cos 2x} \right)dx} = x - \frac{{\sin 2x}}{2} + C\].
Theo giả thiết, ta có: \[F\left( {\frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{4} \Leftrightarrow \frac{\pi }{3} - \frac{1}{2}\sin \frac{{2\pi }}{3} + C = \frac{{\sqrt 3 }}{4} \Rightarrow C = \frac{{\sqrt 3 }}{2} - \frac{\pi }{3}\].
Vậy \[F\left( x \right) = x - \frac{{\sin 2x}}{2} + \frac{{\sqrt 3 }}{2} - \frac{\pi }{3}\].
Do đó \[F\left( {\frac{\pi }{4}} \right) = \frac{\pi }{4} - \frac{1}{2}\sin 2\left( {\frac{\pi }{4}} \right) + \frac{{\sqrt 3 }}{2} - \frac{\pi }{3} = \frac{{\sqrt 3 - 1}}{2} - \frac{\pi }{{12}}\].
Chọn D.
Câu 26:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\begin{array}{l}{\cos ^4}2x = {\left( {\frac{{1 + \cos 4x}}{2}} \right)^2} = \frac{1}{4}\left( {1 + 2\cos 4x + {{\cos }^2}4x} \right)\\\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( {1 + 2\cos 4x + \frac{{1 + \cos 8x}}{2}} \right) = \frac{1}{8}\left( {3 + 4\cos 4x + \cos 8x} \right)\end{array}\]
Do đó \[F\left( x \right) = \frac{1}{8}\int {\left( {3 + 4\cos 4x + \cos 8x} \right)dx} = \frac{1}{8}\left( {3x + \sin 4x + \frac{1}{8}\sin 8x} \right) + C\]
Mà \[F\left( 0 \right) = 2019\] nên ta có \[C = 2019\].
Vậy \[F\left( x \right) = \frac{1}{8}\left( {3x + \sin 4x + \frac{1}{8}\sin 8x} \right) + 2019\].
Do đó \[F\left( {\frac{\pi }{8}} \right) = \frac{{3\pi + 129224}}{{64}}\]
Chọn C.
Câu 27:
Gọi \[F\left( x \right)\] là nguyên hàm của hàm số \[f\left( x \right) = \frac{{{{\cos }^5}x}}{{1 - \sin x}}\], với \[x \ne \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\] và thỏa mãn \[F\left( \pi \right) = \frac{3}{4}\]. Giá trị của \[F\left( { - \frac{\pi }{2}} \right)\] là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta thấy: \[\begin{array}{l}\frac{{{{\cos }^5}x}}{{1 - \sin x}} = {\cos ^3}x\left( {1 + \sin x} \right) = \left( {1 - {{\sin }^2}x} \right)\cos x + {\cos ^3}x.\sin x\\ \Rightarrow F\left( x \right) = \int {\left( {1 - {{\sin }^2}x} \right)d\left( {\sin x} \right)} - \int {{{\cos }^3}xd\left( {\cos x} \right)} = \sin x - \frac{{{{\sin }^3}x}}{3} - \frac{{{{\cos }^4}x}}{4} + C\end{array}\]
Theo giả thiết, ta có \[F\left( \pi \right) = \frac{3}{4}\] nên \[C = 1\].
Vậy \[F\left( x \right) = \sin x - \frac{{{{\sin }^3}x}}{3} - \frac{{{{\cos }^4}x}}{4} + C\]
Do đó \[F\left( { - \frac{\pi }{2}} \right) = \frac{1}{3}\].
Chọn D.
Câu 28:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[v\left( t \right) = S'\left( t \right) = t\] nên \[v\left( {{t_0}} \right) = {t_0} = 5\left( {m/s} \right)\]
Chọn A.
Câu 29:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Chọn mốc thời gian và gốc tọa độ lúc ô tô bắt đầu đạp phanh. Ta có: \[t = 0;s = 0\].
\[\begin{array}{l}s\left( t \right) = \int {v\left( t \right)dt} = \int {\left( {10 - 2t} \right)dt} = 10t - {t^2} + C,\\s\left( 0 \right) = 0 \Rightarrow C = 0 \Rightarrow s\left( t \right) = 10t - {t^2}\end{array}\]
Ô tô dừng hẳn khi \[v\left( t \right) = 0 \Leftrightarrow 10 - 2t = 0 \Leftrightarrow t = 5\].
Trong 8 giây cuối, ô tô chuyển động đều với vận tốc 10 (m/s) trong 3 giây đầu và chuyển động chậm dần đều trong 5 giây cuối.
Quãng đường ô tô di chuyển là: \[s = 3.10 + 10.5 - {5^2} = 55m\].
Chọn C.Câu 30:
Một vật chuyển động với gia tốc \[a\left( t \right) = \frac{3}{{t + 1}}\left( {m/{s^2}} \right)\], trong đó t là khoảng thời gian tính từ thời điểm ban đầu. Vận tốc ban đầu của vật là. Hỏi vận tốc cảu vật tại giây thứ 10 bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Vận tốc của vật tại thời điểm t được tính theo công thức: \[v\left( t \right) = \int {a\left( t \right)dt} = \int {\frac{3}{{t + 1}}dt} = 3\ln \left| {t + 1} \right| + C\]
Vì vận tốc ban đầu (lúc \[t = 0\]) của vật là \[{v_0} = 6m/s\] nên:
\[v\left( 0 \right) = 3\ln \left| {0 + 1} \right| + C = 6 \Leftrightarrow C = 6 \Rightarrow v\left( t \right) = 3\ln \left| {t + 1} \right| + 6\].
Vận tốc của vật chuyển động tại giây thứ 10 là: \[v\left( {10} \right) = 3\ln \left| {10 + 1} \right| + 6 \approx 13,2\left( {m/s} \right)\].
Chọn C.
Câu 31:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Vận tốc \[v\left( t \right)\] chính là nguyên hàm của gia tốc \[a\left( t \right)\] nên ta có:
\[v\left( t \right) = \int {a\left( t \right)dt} = \int {\left( { - \frac{1}{{24}}{t^3} + \frac{5}{{16}}{t^2}} \right)dt} = - \frac{1}{{96}}{t^4} + \frac{5}{{48}}{t^3} + C\]
Tại thời điểm ban đầu \[\left( {t = 0} \right)\] thì vận động viên ở tại vị trí xuất phát nên vận tốc lúc đó là: \[{v_0} = 0 \Rightarrow v\left( 0 \right) = 0 \Leftrightarrow - \frac{1}{{96}}{.0^4} + \frac{5}{{48}}{.0^3} + C = 0 \Leftrightarrow C = 0\].
Vậy công thức vận tốc là \[v\left( t \right) = - \frac{1}{{96}}{t^4} + \frac{5}{{48}}{t^3}\]
Vận tốc của vận động viên tại giây thứ 5 là \[v\left( 5 \right) = 6,51\;m/s\].
Chọn B.
Câu 32:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Xem như tại thời điểm \[{t_0} = 0\] thì nhà khoa học phóng tên lửa với vận tốc đầu 20 m/s. Ta có \[s\left( 0 \right) = 0\] và \[v\left( 0 \right) = 20\].
Vì tên lửa chuyển động thẳng đứng nên gia tốc trọng trường tại mọi thời điểm t là \[{s^n}\left( t \right) = - 9,8\;m/{s^2}\].
Nguyên hàm của gia tốc là vận tốc nên ta có vận tốc của tên lửa tại thời điểm t là \[v\left( t \right) = \int { - 9,8dt} = - 9,8t + {C_1}\].
Do \[v\left( 0 \right) = 20\] nên \[ - 9,8t + {C_1} = 20 \Leftrightarrow {C_1} = 20 \Rightarrow v\left( t \right) = - 9,8t + 20\].
Vậy vận tốc của tên lửa sau 2s là \[v\left( 2 \right) = - 9,8.2 + 20 = 0,4\left( {m/s} \right)\].
Chọn B.
Câu 33:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[A = \int {\frac{{\ln x}}{x}dx} = \int {\ln x\frac{1}{x}dx} \]
Đặt \[u = \ln x \Rightarrow du = \frac{1}{x}dx\]
Do đó \[A = \int {udu} = \frac{{{u^2}}}{2} + C\]
Vậy \[\int {\frac{{\ln x}}{x}dx} = \frac{1}{2}{\ln ^2}x + C\]
Chọn A.
Câu 34:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[u = \sqrt {{x^2} + 1} \Rightarrow {x^2} = {u^2} - 1\] và \[xdx = udu\].
Khi đó \[\begin{array}{l}I = \int {\left( {{u^2} - 1} \right).udu = } \int {\left( {{u^2} - 1} \right)du} \\\;\; = \frac{{{u^3}}}{3} - u + C\end{array}\]
Vậy \[I = \frac{1}{3}\left( {{x^2} + 1} \right)\sqrt {{x^2} + 1} - \sqrt {{x^2} + 1} + C\].
Chọn C.Câu 35:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[u = {x^3} + 1\] ta có \[du = 3{x^2}dx \Rightarrow {x^2}dx = \frac{1}{3}du\]
Suy ra \[\int {f\left( x \right)dx} = \int {{e^u}\frac{1}{3}du} = \frac{1}{3}{e^u} + C\]
Do đó \[F\left( x \right) = \frac{1}{3}{e^{{x^3} + 1}} + C\].
Mặt khác \[F\left( { - 1} \right) = \frac{1}{3}\] nên \[C = 0\]. Vậy \[\int {f\left( x \right)dx} = \frac{1}{3}{e^{{x^3} + 1}}\].
Chọn D.
Câu 36:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[u = 1 + 3\cos x\], ta có \[du = - 3\sin xdx\] hay \[2\sin xdx = - \frac{2}{3}du\].
Khi đó \[M = - \frac{2}{3}\int {\frac{1}{u}du} = - \frac{2}{3}\ln \left| u \right| + C\]
Vậy \[M = \int {\frac{{2\sin x}}{{1 + 3\cos x}}dx} = - \frac{2}{3}\ln \left| {1 + 3\cos x} \right| + C\]
Chọn C.
Câu 37:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[\int {x.\sqrt[3]{{{x^2} + 1}}dx} = \frac{1}{2}\int {{{\left( {{x^2} + 1} \right)}^{\frac{1}{3}}}d\left( {{x^2} + 1} \right)} = \frac{3}{8}{\left( {{x^2} + 1} \right)^{\frac{4}{3}}} + C\].
Chọn A.
Câu 38:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[u = \sqrt {x + 1} \Rightarrow {u^2} = x + 1\]. Suy ra \[x = {u^2} - 1\] và \[dx = 2udu\].
Khi đó \[R = \int {\frac{{2u}}{{\left( {{u^2} - 1} \right)u}}du} = \int {\frac{2}{{{u^2} - 1}}du} = \int {\left( {\frac{1}{{u - 1}} - \frac{1}{{u + 1}}} \right)du} = \ln \left| {\frac{{u - 1}}{{u + 1}}} \right| + C\].
Vậy \[R = \ln \left| {\frac{{\sqrt {x + 1} - 1}}{{\sqrt {x + 1} + 1}}} \right| + C\]
Chọn D.
Câu 39:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Xét \[S = \int {{x^3}\sqrt {{x^2} + 9} dx} = \int {{x^2}\sqrt {{x^2} + 9} xdx} \].
Đặt \[u = \sqrt {{x^2} + 9} \Rightarrow {u^2} = {x^2} + 9\]. Suy ra \[{x^2} = {u^2} - 9\] và \[xdx = udu\].
Khi đó \[S = \int {\left( {{u^2} - 9} \right)u.udu} = \int {\left( {{u^4} - 9{u^2}} \right)du} = \frac{{{u^5}}}{5} - 3{u^3} + C\].
Vậy \[S = \frac{{{{\left( {{x^2} + 9} \right)}^2}\sqrt {{x^2} + 9} }}{5} - 3\left( {{x^2} + 9} \right)\sqrt {{x^2} + 9} + C\]
Chọn A.
Câu 40:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[T = \int {\frac{1}{{x\sqrt {\ln x + 1} }}dx} = \int {\frac{1}{{\sqrt {\ln x + 1} }}d\left( {\ln x + 1} \right)} = 2\sqrt {\ln x + 1} + C\].
Chọn B.
Câu 41:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Xét \[U = \int {\frac{{{{\left( {x - 2} \right)}^{2020}}}}{{{{\left( {x + 1} \right)}^{2022}}}}dx} = \int {{{\left( {\frac{{x - 2}}{{x + 1}}} \right)}^{2020}}\frac{1}{{{{\left( {x + 1} \right)}^2}}}dx} \]
Đặt \[u = \frac{{x - 2}}{{x + 1}} \Rightarrow du = \frac{3}{{{{\left( {x + 1} \right)}^2}}}dx \Rightarrow \frac{1}{3}du = \frac{1}{{{{\left( {x + 1} \right)}^2}}}dx\].
Suy ra. \[U = \frac{1}{3}\int {{u^{2020}}du} = \frac{1}{{6063}}{u^{2021}} + C\]. Vậy \[U = \frac{1}{{6063}}{\left( {\frac{{x - 2}}{{x + 1}}} \right)^{2021}} + C\]
Chọn C.
Câu 42:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[u = 1 + \sqrt {1 + \ln x} \Rightarrow {\left( {u - 1} \right)^2} = 1 + \ln x \Leftrightarrow \ln x = {u^2} - 2u \Rightarrow \frac{{dx}}{x} = \left( {2u - 2} \right)du\].
Khi đó \[\begin{array}{l}V = \int {\frac{{{{\ln }^2}x}}{{x\left( {1 + \sqrt {\ln x + 1} } \right)}}dx} = \int {\frac{{{{\left( {{u^2} - 2u} \right)}^2}}}{u}.\left( {2u - 2} \right)du} \\ = 2\int {\left( {{u^4} - 5{u^3} + 8{u^2} - 4u} \right)du} = \frac{2}{5}{u^5} - \frac{5}{2}{u^4} + \frac{{16}}{3}{u^3} - 4{u^2} + C\end{array}\]
Chọn C.
Câu 43:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[u = \sin 2x \Rightarrow du = 2\cos 2xdx \Rightarrow \frac{1}{2}du = \cos 2xdx\]
Ta có \[\begin{array}{l}F\left( x \right) = \int {{{\sin }^2}2x.{{\cos }^3}2xdx} = \frac{1}{2}\int {{u^2}.\left( {1 - {u^2}} \right)du} = \frac{1}{2}\int {\left( {{u^2} - {u^4}} \right)du} \\\;\;\;\;\;\;\;\; = \frac{1}{6}{u^3} - \frac{1}{{10}}{u^5} + C = \frac{1}{6}{\sin ^3}2x - \frac{1}{{10}}{\sin ^5}2x + C\end{array}\]
\[F\left( {\frac{\pi }{4}} \right) = 0 \Leftrightarrow \frac{1}{6}{\sin ^3}\frac{\pi }{2} - \frac{1}{{10}}{\sin ^5}\frac{\pi }{2} + C = 0 \Leftrightarrow C = - \frac{1}{{15}}\]
Vậy \[F\left( x \right) = \frac{1}{6}{\sin ^3}2x - \frac{1}{{10}}{\sin ^5}2x - \frac{1}{{15}}\]
Do đó \[F\left( {2019\pi } \right) = - \frac{1}{{15}}\]
Chọn A.
Câu 44:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Vì \[x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1 = \left( {{x^2} + 3x} \right)\left( {{x^2} + 3x + 2} \right) + 1 = {\left[ {\left( {{x^2} + 3x} \right) + 1} \right]^2}\] nên ta đặt \[u = {x^2} + 3x\], khi đó \[du = \left( {2x + 3} \right)dx\]
Nguyên hàm ban đầu trở thành \[\int {\frac{{du}}{{{{\left( {u + 1} \right)}^2}}} = - \frac{1}{{u + 1}} + C} \].
Suy ra \[\int {\frac{{\left( {2x + 3} \right)dx}}{{x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1}}} = - \frac{1}{{{x^2} + 3x + 1}} + C\]
Vậy \[g\left( x \right) = {x^2} + 3x + 1;\;g\left( x \right) = 0 \Leftrightarrow {x^2} + 3x + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{ - 3 + \sqrt 5 }}{2}\\x = \frac{{ - 3 - \sqrt 5 }}{2}\end{array} \right.\].
Do đó \[S = \left\{ {\frac{{ - 3 + \sqrt 5 }}{2};\frac{{ - 3 - \sqrt 5 }}{2}} \right\}\].
Tổng giá trị các phần tử của S bằng \[ - 3\].
Chọn C.
Câu 45:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[F\left( x \right) = \int {\frac{x}{{\sqrt {8 - {x^2}} }}dx} = - \int {\frac{1}{{2\sqrt {8 - {x^2}} }}d\left( {8 - {x^2}} \right) = - \sqrt {8 - {x^2}} + C} \]
Mặt khác \[F\left( 2 \right) = 0 \Rightarrow - \sqrt {8 - {x^2}} + C = 0 \Leftrightarrow C = 2\]
Vậy \[F\left( x \right) = - \sqrt {8 - {x^2}} + 2\].
Xét phương trình \[\begin{array}{l}F\left( x \right) = x \Leftrightarrow - \sqrt {8 - {x^2}} + 2 = x \Leftrightarrow \sqrt {8 - {x^2}} = 2 - x \Leftrightarrow \left\{ \begin{array}{l}2 - x \ge 0\\8 - {x^2} = {\left( {2 - x} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\2{x^2} - 4x - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\\left[ \begin{array}{l}x = 1 - \sqrt 3 \Leftrightarrow x = 1 - \sqrt 3 \\x = 1 + \sqrt 3 \end{array} \right.\end{array} \right.\end{array}\]
Chọn D.
Câu 46:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Phân tích \[f\left( x \right) = \frac{{2x + 1}}{{{x^4} + 2{x^3} + {x^2}}} = \frac{{2x + 1}}{{{x^2}{{\left( {x + 1} \right)}^2}}} = \frac{{2x + 1}}{{{{\left( {{x^2} + x} \right)}^2}}}\]
Khi đó \[F\left( x \right) = \int {\frac{{2x + 1}}{{{{\left( {{x^2} + x} \right)}^2}}}dx} = \int {\frac{1}{{{{\left( {{x^2} + x} \right)}^2}}}d\left( {{x^2} + x} \right)} = - \frac{1}{{{x^2} + x}} + C\].
Mặt khác \[F\left( 1 \right) = \frac{1}{2} \Rightarrow - \frac{1}{2} + C = \frac{1}{2} \Rightarrow C = 1\].
Vậy \[F\left( x \right) = - \frac{1}{{{x^2} + x}} + 1 = - \frac{1}{{x\left( {x + 1} \right)}} + 1 = - \left( {\frac{1}{x} - \frac{1}{{x + 1}}} \right) + 1\].
Do đó \[\begin{array}{l}S = F\left( 1 \right) + F\left( 2 \right) + F\left( 3 \right) + ... + F\left( {2019} \right) = - \left( {1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{{2019}} - \frac{1}{{2020}}} \right) + 2019\\\;\;\; = - \left( {1 - \frac{1}{{2020}}} \right) + 2019 = 2018 + \frac{1}{{2020}} = 2018\frac{1}{{2020}}\end{array}\]
Chọn C.
Câu 47:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[f\left( x \right).f'\left( x \right) = \left( {2x + 1} \right)\sqrt {1 + {f^2}\left( x \right)} \Leftrightarrow \frac{{f\left( x \right).f'\left( x \right)}}{{\sqrt {1 + {f^2}\left( x \right)} }} = 2x + 1\].
Suy ra \[\int {\frac{{f\left( x \right).f'\left( x \right)}}{{\sqrt {1 + {f^2}\left( x \right)} }}dx} = \int {\left( {2x + 1} \right)dx} \Leftrightarrow \int {\frac{{d\left( {1 + {f^2}\left( x \right)} \right)}}{{2\sqrt {1 + {f^2}\left( x \right)} }}} = \int {\left( {2x + 1} \right)dx} \Leftrightarrow \sqrt {1 + {f^2}\left( x \right)} = {x^2} + x + C\]
Theo giả thiết \[f\left( 0 \right) = 2\sqrt 2 \], suy ra \[\sqrt {1 + {{\left( {2\sqrt 2 } \right)}^2}} = C \Leftrightarrow C = 3\]
Với \[C = 3\] thì \[\sqrt {1 + {f^2}\left( x \right)} = {x^2} + x + 3 \Rightarrow f\left( x \right) = \sqrt {{{\left( {{x^2} + x + 3} \right)}^2} - 1} \]
Vậy \[f\left( 1 \right) = \sqrt {24} = 2\sqrt 6 \]
Chọn D.
Câu 48:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có: \[{\left( {f\left( x \right)} \right)^2}.f'\left( x \right) = 3{x^2} + 4x + 2\;\;\;\;\;\;\left( * \right)\]
Lấy nguyên hàm hai vế của đẳng thức (*) ta được:
\[\int {{{\left( {f\left( x \right)} \right)}^2}.f'\left( x \right)dx} = \int {\left( {3{x^2} + 4x + 2} \right)dx} \Leftrightarrow \frac{1}{3}{f^3}\left( x \right) = {x^3} + 2{x^2} + 2x + C \Leftrightarrow {f^3}\left( x \right) = 3{x^3} + 6{x^2} + 6x + 3C\]
Theo giả thiết, ta có \[f\left( 0 \right) = 3\] nên
\[{\left( {f\left( 0 \right)} \right)^3} = 3\left( {{0^3} + {{2.0}^2} + 2.0 + C} \right) \Leftrightarrow 27 = 3C \Leftrightarrow C = 9 \Rightarrow {f^3}\left( x \right) = 3{x^3} + 6{x^2} + 6x + 27\]
Ta tìm giá trị lớn nhất của hàm số \[g\left( x \right) = 3{x^3} + 6{x^2} + 6x + 27\] trên đoạn \[\left[ { - 2;1} \right]\].
Ta có \[g'\left( x \right) = 9{x^2} + 12x + 6 > 0,\forall x \in \left[ { - 2;1} \right]\] nên đồng biến trên đoạn \[\left[ { - 2;1} \right]\].
Vậy \[\mathop {\max f\left( x \right)}\limits_{\left[ { - 2;1} \right]} = \sqrt[3]{{\mathop {\max g\left( x \right)}\limits_{\left[ { - 2;1} \right]} }} = \sqrt[3]{{42}}\].
Chọn C.
Câu 49:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[x = 2\sin t\] với \[t \in \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\]. Ta có \[\cos t > 0\] và \[dx = 2\cos tdt\].
Khi đó \[I = \int {\frac{{4{{\sin }^2}t}}{{\sqrt {4 - 4{{\sin }^2}t} }}2\cos tdt} = \int {4{{\sin }^2}tdt} \] (vì \[\cos t > 0,\forall t \in \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\]).
Suy ra \[I = 2\int {\left( {1 - \cos 2t} \right)dt} = 2t - \sin 2t + C\]
Từ \[x = 2\sin t \Rightarrow t = \arcsin \frac{x}{2}\] và \[\sin 2t = 2\sin t.\cos t = \frac{{x\sqrt {4 - {x^2}} }}{2}\]
Vậy \[I = \int {\frac{{{x^2}}}{{\sqrt {4 - {x^2}} }}dx} = 2\arcsin \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{2} + C\]
Chọn D.
Câu 50:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[x = \cos t,t < 0 < \pi \Rightarrow dx = - \sin t.dt\].
Khi đó \[I = - \int {\frac{{\sin t.dt}}{{{{\sin }^3}t}}dt} = - \int {\frac{{dt}}{{{{\sin }^2}t}}} = \cot t + C\] hay \[I = \frac{x}{{\sqrt {1 - {x^2}} }} + C\]
Vậy \[\int {\frac{1}{{\sqrt {{{\left( {1 - {x^2}} \right)}^3}} }}dx} = \frac{x}{{\sqrt {1 - {x^2}} }} + C\]
Chọn B.
Câu 51:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[x = \tan t\] với \[t \in \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\], ta có \[dx = \left( {1 + {{\tan }^2}t} \right)dt\].
Khi đó \[I = \int {\frac{1}{{1 + {{\tan }^2}t}}\left( {1 + {{\tan }^2}t} \right)dt} = \int {dt} = t + C\]
Vậy \[I = \int {\frac{1}{{1 + {x^2}}}dx} = \arctan x + C\]
Chọn A.
Câu 52:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[\left\{ \begin{array}{l}u = x\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = {e^x}\end{array} \right.\]
Khi đó \[\begin{array}{l}\int {x{e^x}dx} = \int {xd{e^x}} = x.{e^x} - \int {{e^x}.dx} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = x.{e^x} - {e^x} + C\end{array}\]
Chọn A.
Câu 53:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[\left\{ \begin{array}{l}u = \ln \left( {x + 2019} \right)\\dv = dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{1}{{x + 2019}}dx\\v = x + 2019\end{array} \right.\]
(ở đây từ \[dv = dx \Rightarrow v = x + C\], ta có thể chọn \[C = 2019\] để việc tính toán đơn giản hơn)
Khi đó
\[\int {\ln \left( {x + 2019} \right)dx} = \left( {x + 2019} \right)\ln \left( {x + 2019} \right) - \int {dx} \]
Vậy \[\int {\ln \left( {x + 2019} \right)dx} = \left( {x + 2019} \right)\ln \left( {x + 2019} \right) - x + C\]
Chọn B.
Câu 54:
 Xem đáp án
Xem đáp án
Đặt \[\left\{ \begin{array}{l}u = \sin x\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \cos xdx\\v = {e^x}\end{array} \right.\]
Khi đó \[\int {{e^x}.\sin xdx} = {e^x}.\sin x - \int {{e^x}.\cos xdx} \]
Đến đây ta phải áp dụng phương pháp từng phần một lần nữa, cụ thể:
Với \[\int {{e^x}.\cos xdx} \] ta thực hiện tương tự như sau:
+ Đặt \[\left\{ \begin{array}{l}u = \cos x\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = - \sin xdx\\v = {e^x}\end{array} \right.\]
+ Khi đó \[\int {{e^x}.\cos xdx} = {e^x}.\cos x + \int {{e^x}.\sin xdx} \]
Vậy \[\begin{array}{l}\;\;\;\;\;\int {{e^x}.\sin xdx} = {e^x}.\sin x - \int {{e^x}.\cos xdx} \\ \Leftrightarrow \int {{e^x}.\sin xdx} = {e^x}.\sin x - \left( {{e^x}.\cos x + \int {{e^x}.\sin xdx} } \right)\\ \Leftrightarrow \int {{e^x}.\sin xdx} = \frac{1}{2}{e^x}.\left( {\sin x - \cos x} \right) + C\end{array}\]
Chọn C.
Câu 55:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[\left\{ \begin{array}{l}u = \ln \left( {2 + {x^2}} \right)\\dv = xdx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{{2x}}{{{x^2} + 2}}dx\\v = \frac{{{x^2} + 2}}{2}\end{array} \right.\]
Khi đó \[I = \frac{{{x^2} + 2}}{2}\ln \left( {{x^2} + 2} \right) - \int {xdx} = \frac{{{x^2} + 2}}{2}\ln \left( {{x^2} + 2} \right) - \frac{{{x^2}}}{2} + C\]
Chọn D.
Câu 56:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đặt \[\left\{ \begin{array}{l}u = \ln \left( {\sin x + 2\cos x} \right)\\dv = \frac{{dx}}{{{{\cos }^2}x}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{{\cos x - 2\sin x}}{{\sin x + 2\cos x}}dx\\v = \tan x + 2 = \frac{{\sin x + 2\cos x}}{{\cos x}}\end{array} \right.\]
Khi đó \[\begin{array}{l}I = \left( {\tan x + 2} \right)\ln \left( {\sin x + 2\cos x} \right) - \int {\frac{{\cos x - 2\sin x}}{{\cos x}}dx} \\\;\; = \left( {\tan x + 2} \right)\ln \left( {\sin x + 2\cos x} \right) - x - 2\ln \left| {\cos x} \right| + C\end{array}\]
Chọn B.
Câu 57:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Phân tích: Ở đây ta sẽ ưu tiên \[u = {x^2}\] là đa thức, tuy nhiên vì bậc của u là 2 nên ta sẽ từng phần hai lần mới thu được kết quả. Nhằm tiết kiệm thời gian, tôi gợi ý với phương pháp “sơ đồ đường chéo” cụ thể như sau:
Bước 1: Chia thành 3 cột:
+ Cột 1: Cột u luôn lấy đạo hàm đến 0.
+ Cột 2: Dùng để ghi rõ dấu của các phép toán đường chéo.
+ Cột 3: Cột dv luôn lấy nguyên hàm đến khi tương ứng với cột 1.
Bước 2: Nhân chéo kết quả của 2 cột với nhau. Dấu của phép nhân đầu tiên sẽ có dấu (+), sau đó đan dấu (-), (+), (-),… rồi cộng các tích lại với nhau.
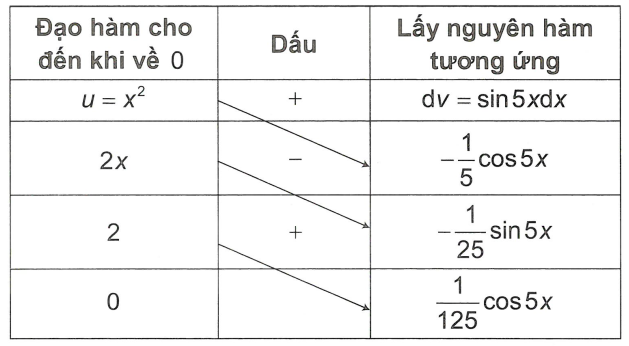
Khi đó \[I = - \frac{1}{5}{x^2}\cos 5x + \frac{2}{{25}}x\sin 5x + \frac{2}{{125}}\cos 5x + C\]
Chọn D.
Câu 58:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Nếu làm thông thường thì từng phần 4 lần ta mới thu được kết quả. Ở đây, chúng tôi trình bày theo sơ đồ đường chéo cho kết quả và nhanh chóng hơn.

Vậy \[I = \left( {\frac{{{x^4}}}{3} - \frac{{4{x^3}}}{{{3^2}}} + \frac{{12{x^2}}}{{{3^3}}} - \frac{{24x}}{{{3^4}}} + \frac{{24}}{{{3^5}}}} \right){e^{3x}} + C\].
Chọn A.
Câu 59:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Phân tích: Sự tồn tại của hàm số mũ và lượng giác trong cùng một nguyên hàm sẽ rất dễ gây cho người học sự nhầm lẫn, nếu ta sẽ không biết điểm dừng thì có thể sẽ bị lạc vào vòng luẩn quẩn. Ở đây, để tìm được kết quả thì ta phải từng phần hai lần như trong ví dụ 3. Tuy nhiên, với sơ đồ đường chéo thì sao? Khi nào sẽ dừng lại?
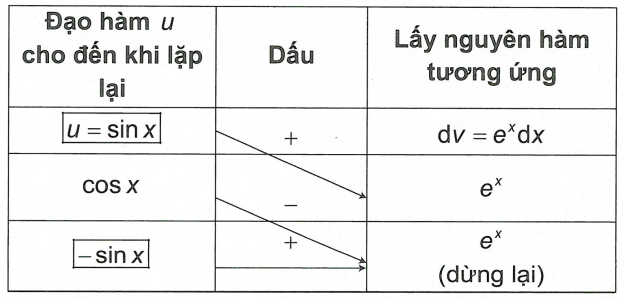
Khi đó, ta sẽ có thể kết luận \[I = {e^x}\sin x - {e^x}\cos x - \int {{e^x}\sin xdx} \].
Hay \[2I = {e^x}\sin x - {e^x}.\cos x\]. Vậy \[I = \frac{1}{2}{e^x}\left( {\sin x - \cos x} \right) + C\]
Chọn C.
Câu 60:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
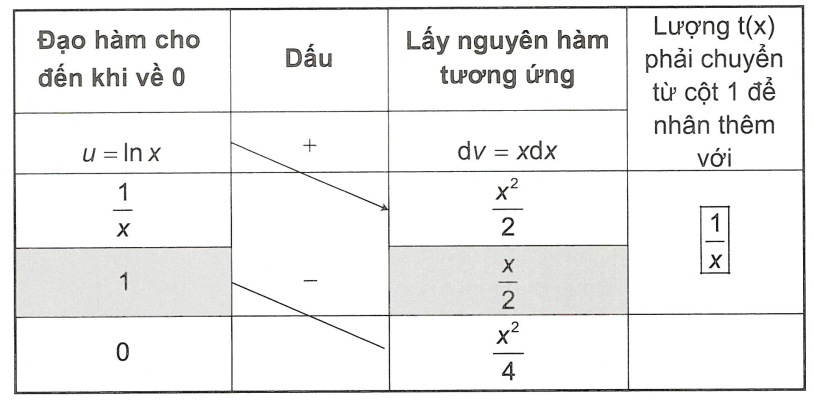
Vậy \[I = \int {x.\ln xdx} = \frac{{{x^2}}}{2}.\ln 2 - \frac{{{x^2}}}{4} + C\]
Chọn A.
Câu 61:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
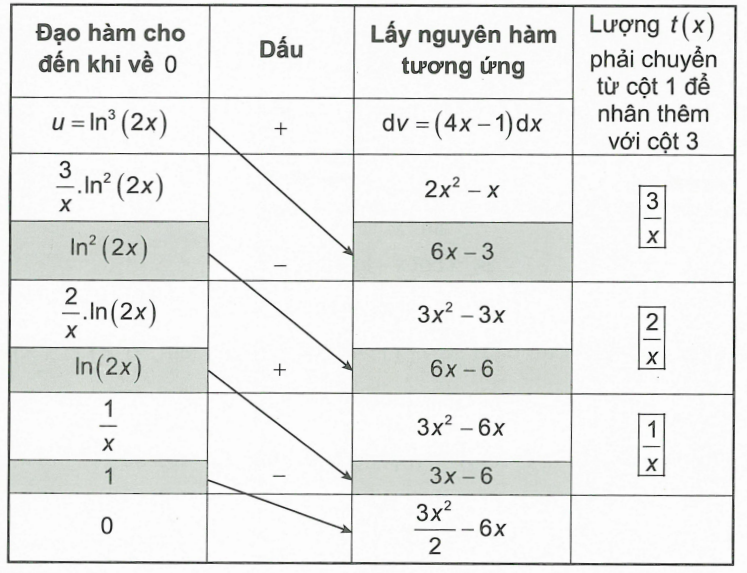
Vậy \[I = \left( {2{x^2} - x} \right){\ln ^3}\left( {2x} \right) - \left( {3{x^2} - 3x} \right){\ln ^2}\left( {2x} \right) + \left( {3{x^2} - 6x} \right)\ln \left( {2x} \right) - \frac{{3{x^2}}}{2} + 6x + C\]
Chọn B.
Câu 62:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có \[F'\left( x \right) = f\left( x \right){e^{2x}} \Leftrightarrow {e^x} + \left( {x - 1} \right){e^x} = f\left( x \right).{e^{2x}} \Leftrightarrow f\left( x \right).{e^{2x}} = x.{e^x}\].
Xét \[\int {f'\left( x \right){e^{2x}}dx} \]
Đặt \[\left\{ \begin{array}{l}u = {e^{2x}}\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = 2{e^{2x}}dx\\v = f\left( x \right)\end{array} \right.\]
Do đó \[I = f\left( x \right).{e^{2x}} - 2\int {f\left( x \right){e^x}dx} = x{e^x} - 2\left( {x - 1} \right){e^x} + C\]
Vậy \[I = \int {f'\left( x \right){e^{2x}}dx} = \left( {2 - x} \right){e^x} + C\]
Chọn A.
