Cho nửa đường tròn đường kính AB. Vẽ hai tiếp tuyến với nửa đường tròn đó. Trên tia Ax lấy điểm M sao cho . Từ M kẻ tiếp tuyến MC với nửa đường tròn (C là tiếp điểm). Tia MC cắt tia By tại D.
Chứng minh MD=MA+BD và tam giác OMD vuông.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Sử dụng tính chất hai tiếp tuyến cắt nhau.
Cách giải:
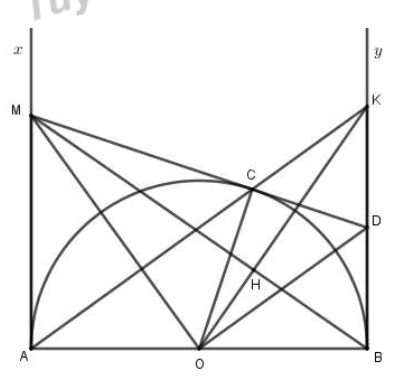
Xét là 2 tiếp tuyến cắt nhau tại M với tiếp điểm A và .
là 2 tiếp tuyến cắt nhau tại D với tiếp điểm B và
Mà
Xét
là 2 tiếp tuyến cắt nhau tại M với tiếp điểm A và là tia phân giác của AOC
là 2 tiếp tuyến cắt nhau tại D với tiếp điểm B và là tia phân giác của COB
Mà AOC và COB là hai góc kề bù
tại D
nên vuông tại O
Cho AM=2R. Tính BD và chu vi tứ giác ABDM
Một chiếc máy bay bay lên với vận tốc 500km/h. Đường bay lên tạo với phương nằm ngang một góc . Hỏi sau 6 phút kể từ lúc cất cánh, máy bay lên cao được bao nhiêu ki-lô-mét theo phương thẳng đứng?
Khi m=2, hãy vẽ đồ thị hàm số đó trên mặt phẳng tọa độ Oxy và tính khoảng cách từ O đến đường thẳng d.
Tia AC cắt tia By tại K. Chứng minh .
Cho hàm số (m là tham số, )
Tìm m để hàm số trên là hàm số đồng biến.
Đường thẳng d cắt đường thẳng tại điểm M. Gọi N và P lần lượt là giao điểm của đường thẳng và với trục hoành Ox. Tìm m để diện tích tam giác OMP bằng 2 lần diện tích tam giác OMN.