 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Cách giải:
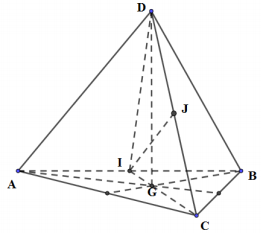
Gọi I, J lần lượt là trung điểm của AB, CD \( \Rightarrow \) I, G, C thẳng hàng.
\( \Rightarrow \)(CGD) cắt tứ diện ABCD bởi thiết diện là tam giác ICD
Ta có: \(I{\rm{D}} = IC = \frac{{a\sqrt 3 }}{2}\) (do là đường cao của tam giác đều cạnh a)
\( \Rightarrow \Delta IC{\rm{D}}\) cân tại I \( \Rightarrow IJ \bot CD\)
\(\Delta IJC\) vuông tại J \( \Rightarrow IJ = \sqrt {I{C^2} - J{C^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
Diện tích \(\Delta IC{\rm{D}}\) là: \(S = \frac{1}{2}IJ.CD = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.a = \frac{{{a^2}\sqrt 2 }}{4}\).
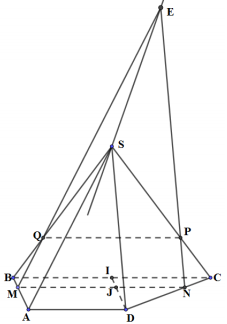
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?
Giải các phương trình sau:
a) \(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0\)