 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
Xác định thiết diện dựa vào các yếu tố song song.
Cách giải:
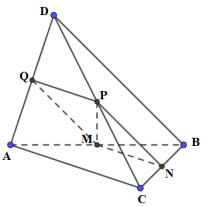
Gọi Q là trung điểm của AD.
Ta có: \(PQ//AC\) (do PQ là đường trung bình của tam giác ACD)
\(MN//AC\) (do MN là đường trung bình của tam giác ABC).
\( \Rightarrow PQ//MN \Rightarrow \) M, N, P, Q đồng phẳng \( \Rightarrow \)\(Q \in \left( {MNP} \right)\)
\( \Rightarrow \)Thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là tứ giác MNQP.
Ta có: \(PQ//MN,\,PQ = MN\left( { = \frac{1}{2}AC} \right) \Rightarrow \)MNQP là hình bình hành
Vậy, thiết diện của tứ diện cắt bởi mp(MNP) là hình bình hành.
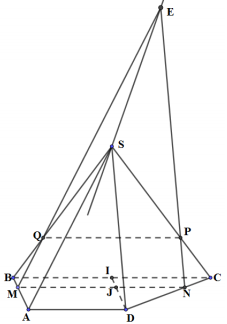
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?
Giải các phương trình sau:
a) \(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0\)