 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Cách giải:
Gọi số học sinh nam của trường là n (học sinh, \(n \in \mathbb{N}\))
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{n + 10}^5\)
Xác suất để cả 5 học sinh được chọn toàn nam: \(\frac{{C_n^5}}{{C_{n + 10}^5}}\).
Xác suất trong 5 học sinh được chọn có 2 nữ: \(\frac{{C_{10}^2C_n^3}}{{C_{n + 10}^5}}\).
Theo đề bài, ta có:
\(\frac{{C_n^5}}{{C_{n + 10}^5}} = \frac{7}{{15}}.\frac{{C_{10}^2C_n^3}}{{C_{n + 10}^5}} \Leftrightarrow 15C_n^5 = 7C_{10}^2C_n^3 \Leftrightarrow 15C_n^5 = 7.45C_n^3 \Leftrightarrow C_n^5 = 21C_n^3 \Leftrightarrow \frac{{n!}}{{5!\left( {n - 5} \right)!}} = \frac{{21.n!}}{{3!\left( {n - 3} \right)!}}\)
\( \Leftrightarrow \frac{{n!}}{{5!\left( {n - 5} \right)!}} = \frac{{21.n!}}{{3!\left( {n - 3} \right)!}} \Leftrightarrow 5.4 = \frac{{\left( {n - 3} \right)\left( {n - 4} \right)}}{{21}} \Leftrightarrow {n^2} - 7n + 12 - 420 = 0 \Leftrightarrow {n^2} - 7n - 408 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 24\,\left( {TM} \right)\\n = - 17\,\left( L \right)\end{array} \right.\)\( \Rightarrow \) Số học sinh nam của lớp 11A là: 24 học sinh.
\( \Rightarrow \)Lớp 11A có tất cả số học sinh là: \(10 + 24 = 34\) (học sinh)
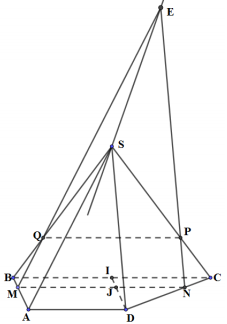
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?
Giải các phương trình sau:
a) \(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0\)