Từ điểm A nằm ngoài đường tròn ta kẻ hai tiếp tuyến AM và AN đến đường tròn (M và N là tiếp điểm). Đường thẳng MO cắt đường tròn tại điểm P. Đường thẳng vuông góc với OA tại O cắt AN tại C và cắt AM tại B.
Chứng minh bốn điểm A, M, O, N cùng thuộc một đường tròn.
Giải bởi Vietjack
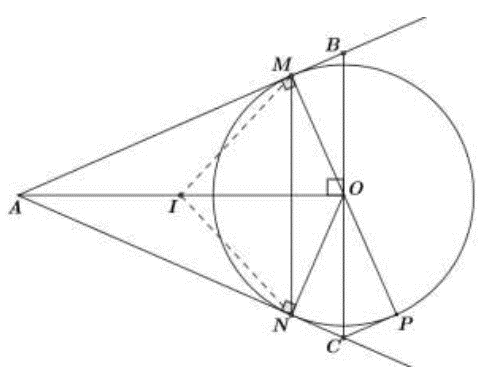
Gọi I là trung điểm của AO.
Ta có: AM, AN là tiếp tuyến của đường tròn tại M và N.
vuông tại M và N.
A, M, O, N cùng thuộc đường tròn tâm I (t/c).
Vậy bốn điểm A, M, O, N cùng thuộc một đường tròn.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng .
Xác định m để hàm số đồng biến.
Cho tam giác ABC vuông tại A có AB= 3cm, AC=4cm. Kẻ đường cao . Tính BH, CH.
Xác định giá trị của m để đường thẳng đi qua điểm . Vẽ đồ thị ứng với m tìm được.
Cho tam giác ABC có AB=3,6cm, AC=4,8cm, BC=6cm. Tính các góc B, C (viết kết quả dạng độ, phút, giây) và đường cao AH của tam giác ABC.
Xác định giá trị của m để đường thẳng cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.
Chứng minh CP là tiếp tuyến tại P với đường tròn. Suy ra MB=CN.
