 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn A
Từ \(f'(x) = x{(x + 3)^2},\forall x \in R\)
Ta suy ra bảng xét dấu của \(f'(x)\) là

Từ bảng xét dấu ta thấy \(f'(x)\) chỉ đổi dấu khi \(x\) qua \(x = 0\)
\( \Rightarrow \) Hàm số đạt cực trị tại \(x = 0\)
\( \Rightarrow \) Số điểm cực trị của hàm số đã cho là 1.
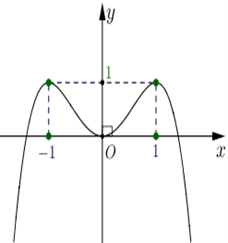
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.
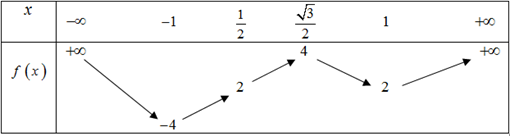
Số giá trị nguyên của tham số \(m\) để phương trình \({f^2}\left( {{\rm{cos}}x} \right) + \left( {3 - m} \right)f\left( {{\rm{cos}}x} \right) + 2m - 10 = 0\) có đúng 4 nghiệm phân biệt thuộc đoạn \(\left[ { - \frac{\pi }{3};\pi } \right]\) là