Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.
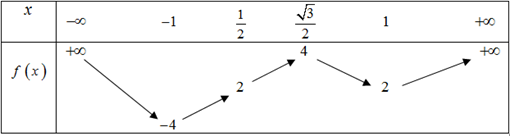
Số giá trị nguyên của tham số \(m\) để phương trình \({f^2}\left( {{\rm{cos}}x} \right) + \left( {3 - m} \right)f\left( {{\rm{cos}}x} \right) + 2m - 10 = 0\) có đúng 4 nghiệm phân biệt thuộc đoạn \(\left[ { - \frac{\pi }{3};\pi } \right]\) là
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn B
Xét \({f^2}\left( {{\rm{cos}}x} \right) + \left( {3 - m} \right)f\left( {{\rm{cos}}x} \right) + 2m - 10 = 0\). Ta có \({\rm{\Delta }} = {\left( {m - 7} \right)^2}\).
Do đó \(\left[ {\begin{array}{*{20}{l}}{f\left( {{\rm{cos}}x} \right) = m - 5\;\left( 1 \right)}\\{f\left( {{\rm{cos}}x} \right) = 2\;\left( 2 \right)}\end{array}} \right.\).
Với \(f\left( {{\rm{cos}}x} \right) = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{cos}}x = a < - 1}\\{{\rm{cos}}x = \frac{1}{2}}\\{{\rm{cos}}x = 1}\end{array}} \right.\).
Trường hợp này được 3 nghiệm trong \(\left[ { - \frac{\pi }{3};\pi } \right]\).
Để phương trình đã cho có đúng 4 nghiệm phân biệt thuộc đoạn \(\left[ { - \frac{\pi }{3};\pi } \right]\) thì (1) có đúng 1 nghiệm trong \(\left[ { - \frac{\pi }{3};\pi } \right]\) và không trùng với nghiệm của các phương trình \({\rm{cos}}x = \frac{1}{2};{\rm{cos}}x = 1\)
\( \Leftrightarrow f\left( t \right) = m - 5\) với \(t = {\rm{cos}}x\) có đúng 1 nghiệm trong \(\left[ { - 1;\frac{1}{2}} \right)\) \( \Rightarrow - 4 \le m - 5 < 2 \Leftrightarrow 1 \le m < 7\).
Do m nguyên nên có 6 giá trị của m thỏa mãn.