 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn D
Gọi \[x\,\,\,(x > 0)\] là độ dài cạnh của hình lập phương. Thể tích của hình lập phương \[V = {x^3}\]
Theo giả thiết cạnh của hình lập phương tăng lên \[k\] lần thì cạnh của hình lập phương là \[kx\]. Do đó thể tích hình lập phương sau khi tăng cạnh là \[{V_1} = {\left( {kx} \right)^3} = {k^3}{x^3} = {k^3}V\].
Vậy thể tích khối lập phương tăng lên \[{k^3}\] lần.
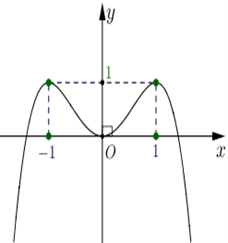
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.
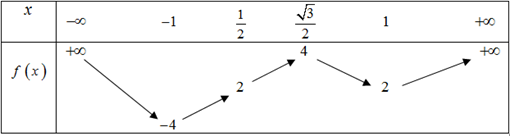
Số giá trị nguyên của tham số \(m\) để phương trình \({f^2}\left( {{\rm{cos}}x} \right) + \left( {3 - m} \right)f\left( {{\rm{cos}}x} \right) + 2m - 10 = 0\) có đúng 4 nghiệm phân biệt thuộc đoạn \(\left[ { - \frac{\pi }{3};\pi } \right]\) là