Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi E, D lần lượt là giao điểm của các tia phân giác trong và ngoài của hai góc B và C. Đường thẳng ED cắt BC tại I cắt cung nhỏ BC ở M. Chứng minh :
a) Ba điểm A, E, D thẳng hàng
b) Tứ giác BECD nội tiếp được trong đường tròn
c) BI.IC = ID.IE
Giải bởi Vietjack
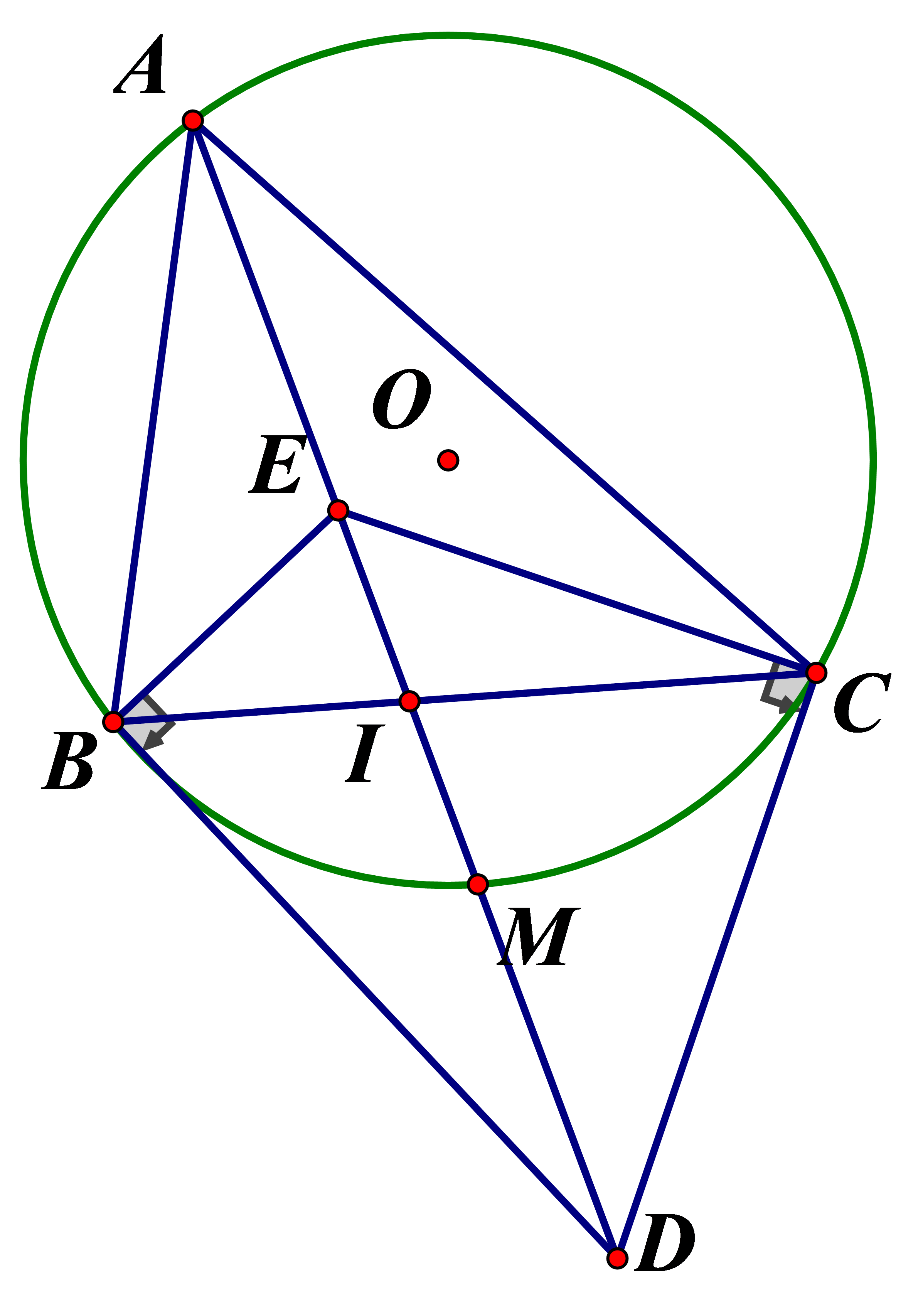
a) Vì \(E\)là giao điểm của hai phân giác \(\angle B\)và \(\angle C\)của tam giác \(ABC\)nên \(AE\)cũng là phân giác của \(\angle A\). Khi đó \(AE,AD\)đều là phân giác trong \(\angle BAC\)nên
\(A,E,D\)thẳng hàng
b) Ta có : \(\angle EBD + \angle ECD = 90^\circ + 90^\circ = 180^\circ \Rightarrow BECD\)là tứ giác nội tiếp
c) Xét \(\Delta BIE\)và \(\Delta DIC\)có : \(\angle EBC = \angle EDC\)(cùng chắn ; \(\angle BIE = \angle DIC\)(đối đỉnh) \( \Rightarrow \frac{{BI}}{{ID}} = \frac{{IE}}{{IC}} \Rightarrow BI.IC = ID.IE\)
4. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng số đo của góc nội tiếp 
. Số đo của cung 
bằng:
có nghiệm
có hai nghiệm là 
Khi đó 
bằng:
