- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Đề kiểm tra giữa học kì 2 môn Toán 9 (Mới nhất)_đề 25
-
14277 lượt thi
-
15 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
. Số đo của cung 
bằng:
Câu 6:
Xem đáp án
Đáp án: D
Khi đó 
bằng:
có hai nghiệm là 
Câu 10:
Xem đáp án
Đáp án: Đ
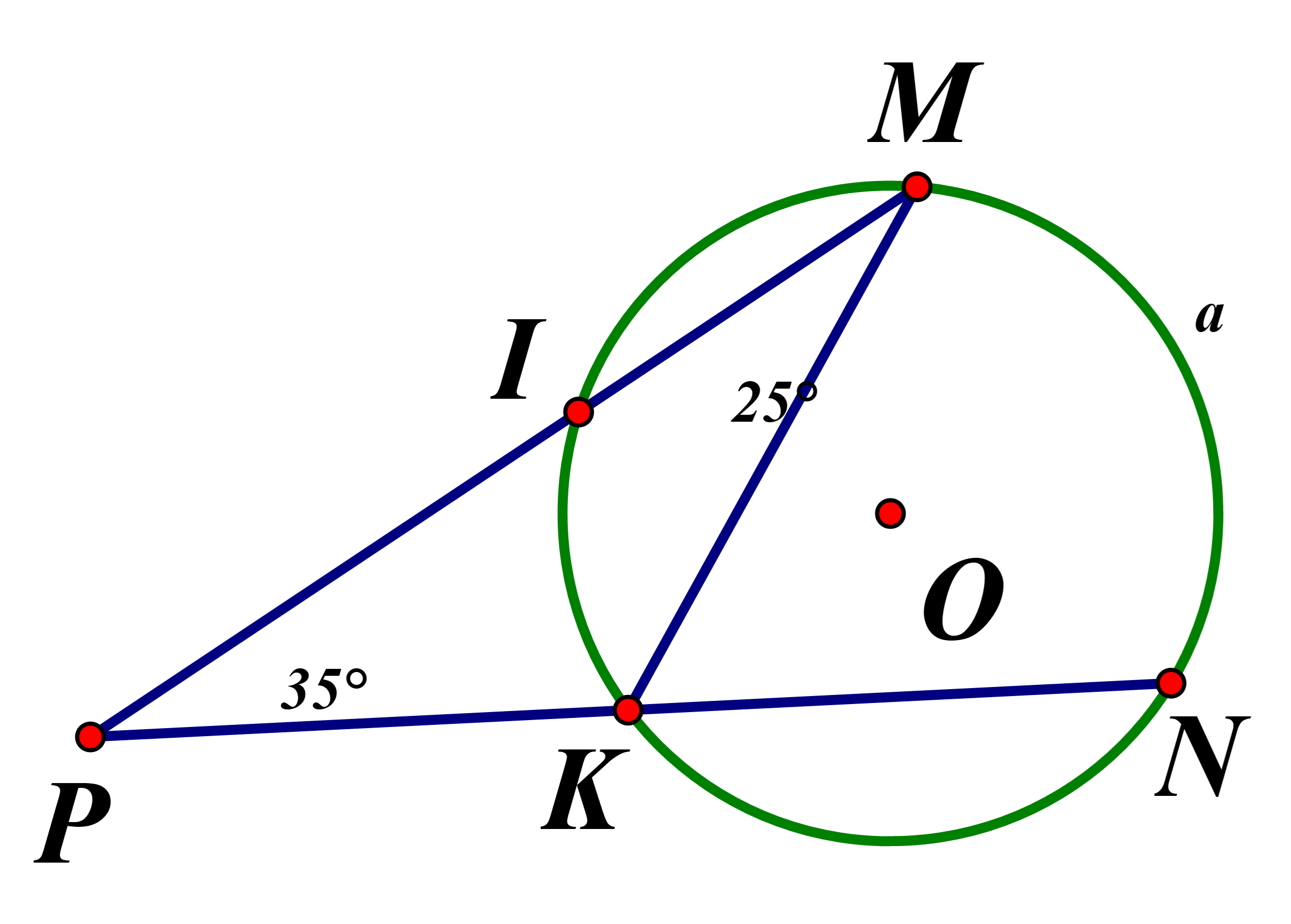
Câu 11:
4. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng số đo của góc nội tiếp 
Xem đáp án
Đáp án: S
Câu 12:
a) Giải hệ phương trình :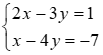 
b) Giải phương trình : 
Xem đáp án
\(a)\left\{ \begin{array}{l}2x - 3y = 1\\x - 4y = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 3\end{array} \right. & & b){x^4} - 5{x^2} + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} = 4\\{x^2} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm 2\\x = \pm 1\end{array} \right.\)
Câu 13:
Tìm các giá trị của m để phương trình 
có nghiệm
Xem đáp án
\(2{x^2} - \left( {4m + 3} \right)x + 2{m^2} - 1 = 0 & (1)\)
\(\Delta = {\left( {4m + 3} \right)^2} - 4.2\left( {2{m^2} - 1} \right) = 24m + 17\)
Để \(\left( 1 \right)\)có nghiệm thì \(\Delta \ge 0 \Leftrightarrow 24m + 17 \ge 0 \Leftrightarrow m \ge \frac{{ - 17}}{{24}}\)
Câu 14:
Xem đáp án
Gọi \(x\)là vận tốc xe khách, \(y\)là vận tốc xe du lịch \(\left( {x > 0,y > 20} \right);25' = \frac{5}{{12}}h\)
Theo bài ta có hệ : \(\left\{ \begin{array}{l}x - y = 20\\\frac{{100}}{y} - \frac{{100}}{x} = \frac{5}{{12}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = 60(tm) \Rightarrow x = 80(tm)\\y = - 80(ktm)\end{array} \right.\)
Vậy vận tốc xe du lịch: 80km/h, vận tốc xe khách: \(60km/h\)
Câu 15:
Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi E, D lần lượt là giao điểm của các tia phân giác trong và ngoài của hai góc B và C. Đường thẳng ED cắt BC tại I cắt cung nhỏ BC ở M. Chứng minh :
a) Ba điểm A, E, D thẳng hàng
b) Tứ giác BECD nội tiếp được trong đường tròn
c) BI.IC = ID.IE
Xem đáp án
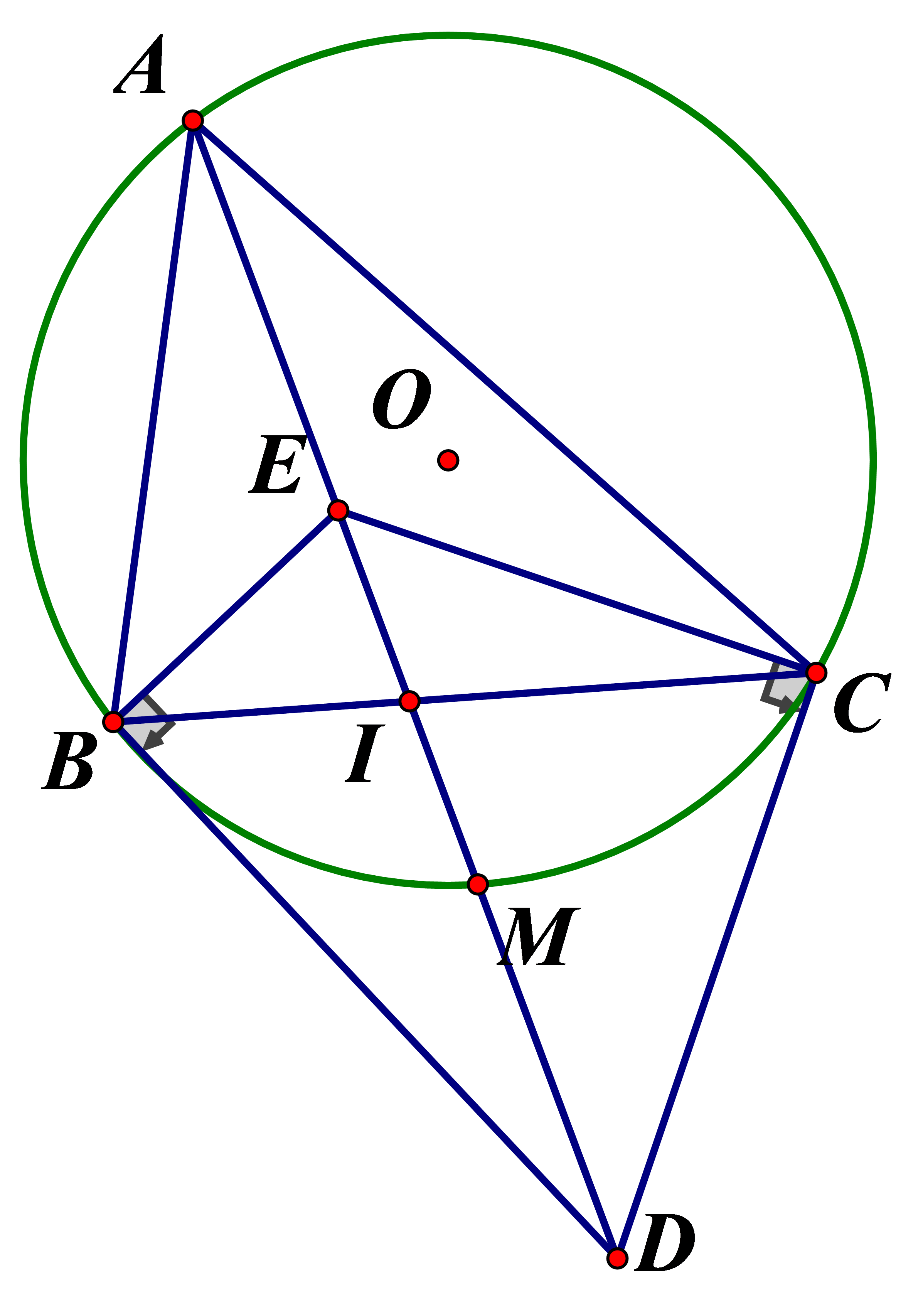
a) Vì \(E\)là giao điểm của hai phân giác \(\angle B\)và \(\angle C\)của tam giác \(ABC\)nên \(AE\)cũng là phân giác của \(\angle A\). Khi đó \(AE,AD\)đều là phân giác trong \(\angle BAC\)nên
\(A,E,D\)thẳng hàng
b) Ta có : \(\angle EBD + \angle ECD = 90^\circ + 90^\circ = 180^\circ \Rightarrow BECD\)là tứ giác nội tiếp
c) Xét \(\Delta BIE\)và \(\Delta DIC\)có : \(\angle EBC = \angle EDC\)(cùng chắn ; \(\angle BIE = \angle DIC\)(đối đỉnh) \( \Rightarrow \frac{{BI}}{{ID}} = \frac{{IE}}{{IC}} \Rightarrow BI.IC = ID.IE\)