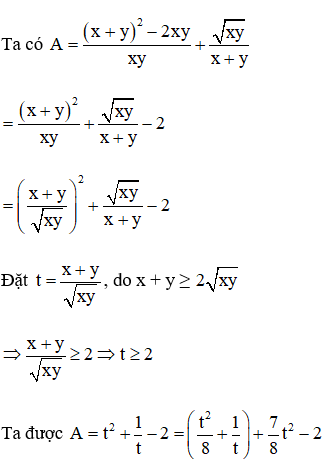- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 17
-
15454 lượt thi
-
5 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
với x ≥ 0; x ≠ 25.
1) Tính giá trị của biểu thức A khi .
2) Rút gọn biểu thức B.
3) Cho . Tìm số nguyên tố x sao cho |M| = −M.
 Xem đáp án
Xem đáp án
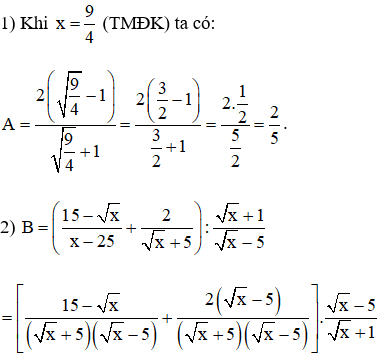
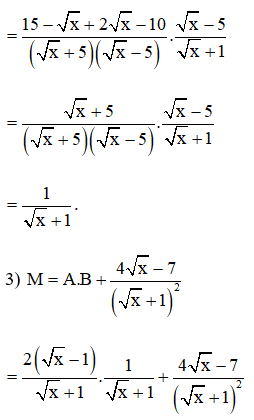
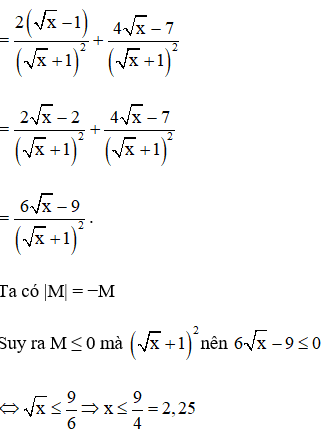
Ta có 0 ≤ x ≤ 2,25 và x là số nguyên tố nên x = 2
Vậy x = 2 thỏa mãn bài toán.
Câu 2:
Giải bài toán bằng cách lập hệ phương trình.
Do ảnh hưởng của dịch Covid – 19 nên trong tháng hai cả hai tổ công nhân chỉ làm được 700 sản phẩm. Sang tháng ba, tình hình dịch ổn định tổ I vượt mức 20%, tổ II vượt mức 15% nên cả hai tổ làm được 830 sản phẩm. Hỏi trong tháng hai mỗi tổ làm được bao nhiêu sản phẩm?
 Xem đáp án
Xem đáp án
Gọi x và y lần lượt là số sản phẩm mà tổ I và tổ II làm được trong tháng 2 (700 > x, y > 0)
Tháng 2 hai tổ làm được 700 sản phẩm nên ta có: x + y = 700 (sản phẩm) (1)
Số sản phẩm tổ I làm được trong tháng 3 là: x + 20%.x = 1,2x (sản phẩm)
Số sản phẩm tổ II làm được trong tháng 3 là: y + 15%.y = 1,15y (sản phẩm)
Tháng 3 hai tổ làm được 830 sản phẩm nên ta có: 1,2x + 1,15y = 830 (sản phẩm) (2)
Từ (1) và (2) ta có hệ phương trình:
(thỏa mãn)
Vậy trong tháng 2 tổ I làm được 500 sản phẩm, tổ II làm được 200 sản phẩm.
Câu 3:
1) Giải hệ phương trình
2) Cho phương trình ẩn x: x2 – 5x + m + 4 = 0 (1)
a) Giải phương trình (1) với m = 2
b) Tìm m để phương trình (1) có 2 nghiệm phân biệt x1; x2 thỏa mãn
 Xem đáp án
Xem đáp án




Thay vào (2) ta được:
52 – 2(m + 4) = 23
=> −2m = 6
=> m = −3 (thỏa)
Vậy m = −3 thỏa giá trị bài toánCâu 4:
Một tàu ngầm đang ở trên mặt biển thì lặn xuống theo phương tạo với mặt nước biển một góc 20°. Hỏi nếu tàu chuyển động theo phương lặn xuống được 200m thì nó ở độ sâu bao nhiêu mét so với mặt nước biển?
Câu 2: Cho (O; R) đường kính AB cố định. Lấy I thuộc OB sao cho . Dây MN ⊥ AB tại I. Điểm F chuyển động trên cung nhỏ AM (F ≠ A, F ≠ M). Tia AF cắt MN tại K. Nối BF cắt MN tại H.
a) Chứng minh: Tứ giác AFHI nội tiếp đường tròn.
b) Chứng minh: AF.AK =AB.AI .
c) Chứng minh từ đó chứng minh đường tròn ngoại tiếp ∆BHK luôn đi qua một điểm cố định khi F chuyển động trên cung nhỏ AM.
 Xem đáp án
Xem đáp án
Câu 1:
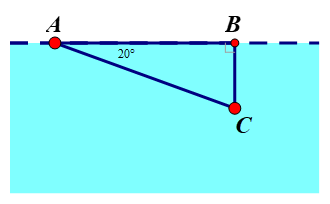
Ta có theo đề bài thì AC = 200m.
Độ sâu so với mặt nước biển là BC.
Xét tam giác ABC vuông tại B.
Suy ra BC = AC. = 200 . sin 20° ≈ 68,4 (m).
Vậy độ sâu so với mặt nước biển là 68,4 m
Câu 2:
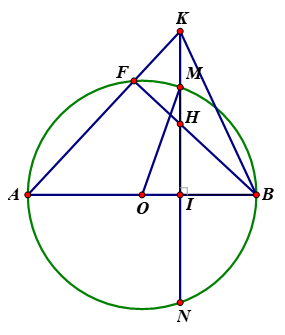
a) Ta có \(góc nội tiếp chắn nửa đường tròn)
(AB ⊥ MN)
Xét tứ giác AFHI có
Suy ra tứ giác AFIH nội tiếp.
b) Xét ∆ AKI và ∆ ABF có:
là góc chung
(chứng minh trên)
Suy ra ∆ AKI ![]() ∆ ABF (g.g)
∆ ABF (g.g)
Từ đó suy ra (1)
Ta có AB = 2R.
AI = AB – IB = 2R =
Suy ra AB.AI = 2R. (2)
Từ (1) và (2) suy ra điều phải chứng minh.
c) Tứ giác AFHI nội tiếp nên .
Đường tròn ngoại tiếp ∆BHK luôn đi qua điểm B cố định