5 câu hỏi trắc nghiệm thuộc Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 12

Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40

Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 12

14525 lượt thi
5 câu hỏi
90 phút

Danh sách câu hỏi

Câu 1:

Cho hai biểu thức $A = \frac{\sqrt{x} + 1}{x - 4}$ và $B = \frac{18 - \sqrt{x}}{x - 4} + \frac{4}{2 - \sqrt{x}} + \frac{\sqrt{x} + 3}{\sqrt{x} + 2}$ với x ≥ 0, x ≠ 4.

1) Tính giá trị của A khi x = 25.

2) Rút gọn biểu thức B.

3) Đặt P = A.B. Tìm giá trị lớn nhất của biểu thức P.

Xem đáp án

1) Khi x = 25 (TMĐK) ta có:

$A = \frac{\sqrt{25} + 1}{25 - 4} = \frac{5 + 1}{21} = \frac{6}{21} = \frac{2}{7}$ .

Vậy giá trị của A khi x = 25 là $A = \frac{2}{7}$ .

2) $B = \frac{18 - \sqrt{x}}{x - 4} + \frac{4}{2 - \sqrt{x}} + \frac{\sqrt{x} + 3}{\sqrt{x} + 2}$

$= \frac{18 - \sqrt{x}}{(\sqrt{x} + 2) (\sqrt{x} - 2)} - \frac{4}{\sqrt{x} - 2} + \frac{\sqrt{x} + 3}{\sqrt{x} + 2}$

$= \frac{18 - \sqrt{x}}{(\sqrt{x} - 2) (\sqrt{x} + 2)} - \frac{4 (\sqrt{x} + 2)}{(\sqrt{x} - 2) (\sqrt{x} + 2)} + \frac{(\sqrt{x} + 3) (\sqrt{x} - 2)}{(\sqrt{x} - 2) (\sqrt{x} + 2)}$

$= \frac{18 - \sqrt{x}}{(\sqrt{x} - 2) (\sqrt{x} + 2)} - \frac{4 \sqrt{x} + 8}{(\sqrt{x} - 2) (\sqrt{x} + 2)} + \frac{x + \sqrt{x} - 6}{(\sqrt{x} - 2) (\sqrt{x} + 2)}$

$= \frac{18 - \sqrt{x} - 4 \sqrt{x} - 8 + x + \sqrt{x} - 6}{(\sqrt{x} - 2) (\sqrt{x} + 2)}$

$= \frac{x - 4 \sqrt{x} + 4}{(\sqrt{x} - 2) (\sqrt{x} + 2)}$

$= \frac{{(\sqrt{x} - 2)}^{2}}{(\sqrt{x} - 2) (\sqrt{x} + 2)}$ .

3) P = A.B $= \frac{\sqrt{x} + 1}{x - 4} . \frac{\sqrt{x} - 2}{\sqrt{x} + 2}$

$= \frac{\sqrt{x} + 1}{(\sqrt{x} + 2) (\sqrt{x} - 2)} . \frac{\sqrt{x} - 2}{\sqrt{x} + 2}$

= $= \frac{\sqrt{x} + 1}{{(\sqrt{x} + 2)}^{2}} = \frac{\sqrt{x} + 1}{x + 4 \sqrt{x} + 4}$

$= \frac{\frac{1}{4} x + \sqrt{x} + 1 - \frac{1}{4} x}{x + 4 \sqrt{x} + 4} = \frac{1}{4} - \frac{1}{4} \frac{{\sqrt{x}}^{2}}{{(\sqrt{x} + 2)}^{2}}$

$\frac{1}{4} - \frac{1}{4} . {(\frac{\sqrt{x}}{\sqrt{x} + 2})}^{2} = \frac{1}{4} - \frac{1}{4} {(1 - \frac{2}{\sqrt{x} + 2})}^{2}$

Ta có $\sqrt{x} \geq 0 \Leftrightarrow \sqrt{x} + 2 \geq 2$

$\Leftrightarrow \frac{2}{\sqrt{x} + 2} \leq \frac{2}{2} \Leftrightarrow - \frac{1}{\sqrt{x} + 2} \geq - 1$

$\Leftrightarrow 1 - \frac{1}{\sqrt{x} + 2} \geq 1 - 1 = 0$

$\Leftrightarrow {(1 - \frac{1}{\sqrt{x} + 2})}^{2} \geq 0 \Leftrightarrow - \frac{1}{4} {(1 - \frac{1}{\sqrt{x} + 2})}^{2} \leq 0 \Leftrightarrow - \frac{1}{4} {(1 - \frac{1}{\sqrt{x} + 2})}^{2} \leq 0 \Leftrightarrow P = \frac{1}{4} - \frac{1}{4} {(1 - \frac{1}{\sqrt{x} + 2})}^{2} \leq \frac{1}{4}$ .

Vậy giá trị lớn nhất của P là $\frac{1}{4}$ . Dấu bằng xảy ra khi $\sqrt{x} = 0 \Leftrightarrow x = 0$ .

Câu 2:

Giải bài toán bằng cách lập hệ phương trình

Trong tháng đầu, hai tổ làm được 600 sản phẩm. Sang tháng thứ 2, tổ I vượt mức 10% và tổ II vượt mức 20% so với tháng đầu, do đó tháng thứ hai cả hai tổ làm được 685 sản phẩm. Hỏi tháng đầu, mỗi tổ làm được bao nhiêu sản phẩm?

Xem đáp án

Gọi x (sản phẩm) là số sản phẩm mà tổ I làm trong tháng đầu (0 < x < 600, x ∈ ℕ).

y (sản phẩm) là số sản phẩm mà tổ II làm trong tháng đầu (0 < y < 600, y ∈ ℕ).

Trong tháng đầu, hai tổ làm được 600 sản phẩm ta có:

x + y = 600 (sản phẩm) (1)

Số sản phẩm mà tổ I làm được trong tháng hai là:

x + 10%x = 1,1x (sản phẩm)

Số sản phẩm mà tổ II làm được trong tháng hai là:

y + 20%y = 1,2y (sản phẩm)

Tháng thứ hai cả hai tổ làm được 685 sản phẩm ta có:

1,1x + 1,2y = 685 (sản phẩm) (2)

Từ (1) và (2) ta có hệ phương trình: $\{\begin{cases} x + y = 600 \\ 1, 1 x + 1, 2 y = 685 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = 600 - y \\ 1, 1 (600 - y) + 1, 2 y = 685 \end{cases} \Leftrightarrow \{\begin{cases} x = 600 - y \\ 660 - 1, 1 y + 1, 2 y = 685 \end{cases} \Leftrightarrow \{\begin{cases} x = 600 - y \\ 0, 1 y = 25 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = 350 \\ y = 250 \end{cases}$ (thỏa mãn)

Vậy trong tháng thứ nhất tổ I làm được 350 sản phẩm, tổ II làm được 250 sản phẩm.

Câu 3:

1) Trong cùng mặt phẳng tọa độ Oxy, cho parabol (P): y = x² và đường thẳng

(d): y = x + 2. Tìm tọa độ các giao điểm của (P) và (d). Vẽ (P) và (d).

2) Cho hệ phương trình $\{\begin{cases} m x + y = 2 m \\ x + m y = m + 1 \end{cases}$

Tìm m để hệ đã cho có nghiệm duy nhất (x; y) mà cả x và y đều nhận giá trị nguyên.

Xem đáp án

1) Phương trình hoành độ giao điểm của (P) và (d) là:

x² = x + 2

Û x² – x – 2 = 0

Û x² – 2x + x −2 = 0

Û x(x – 2) + (x – 2) = 0

Û (x + 1)(x − 2) = 0

$\Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array}$

• Với x = −1 thì y = x + 2 = –1 + 2 = 1.

Do đó, ta có tọa độ giao điểm của (P) và (d) là A(−1; 1).

• Với x = 2 thì y = x + 2 = 2 + 2 = 4.

Do đó, ta có tọa độ giao điểm của (P) và (d) là B(2; 4).

Vậy hai đồ thị hàm số trên có 2 giao điểm là A(−1; 1) và B(2; 4).

Vẽ (P)

Bảng giá trị:

x	−2	−1	0	1	2
y = x²	4	1	0	1	4

Vẽ (d)

(d) y = x + 2 đi qua 2 điểm A(−1; 1) và B(2; 4).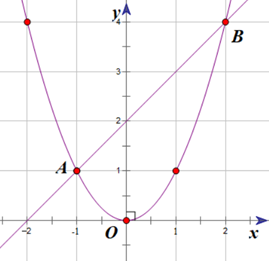

1) Trong cùng mặt phẳng tọa độ Oxy, cho parabol (P): (ảnh 1)

2) Để hệ phương trình có nghiệm duy nhất thì:

$\frac{m}{1} \neq \frac{1}{m} \Leftrightarrow m^{2} \neq 1 \Leftrightarrow m \neq \pm 1$

Giải hệ phương trình với m là tham số

$\{\begin{cases} m x + y = 2 m \\ x + m y = m + 1 \end{cases} \Leftrightarrow \{\begin{cases} x = m + 1 - m y \\ m (m + 1 - m y) + y = 2 m \end{cases} \Leftrightarrow \{\begin{cases} x = m + 1 - m y \\ m^{2} + m - m^{2} y + y = 2 m \end{cases} \Leftrightarrow \{\begin{cases} x = m + 1 - m y \\ y (1 - m^{2}) = m - m^{2} \end{cases} \Leftrightarrow \{\begin{cases} x = m + 1 - m y \\ y = \frac{m - m^{2}}{1 - m^{2}} = \frac{m (1 - m)}{(1 - m) (1 + m)} = \frac{m}{1 + m} \end{cases} \Leftrightarrow \{\begin{cases} x = m + 1 - m . \frac{m}{1 + m} \\ y = \frac{m}{1 + m} \end{cases}$

Để hệ có nghiệm x, y nguyên thì

$\{\begin{cases} x = m + 1 - m . \frac{m}{1 + m} \\ y = \frac{m}{1 + m} \end{cases}$ nguyên $\Leftrightarrow \frac{m}{1 + m}$ nguyên

Xét $\frac{m}{1 + m} = \frac{m + 1 - 1}{m + 1} = 1 - \frac{1}{m + 1}$

Để $\frac{m}{1 + m}$ nguyên thì m + 1 bằng các giá trị {−1; 1}.

Do đó m ∈ {−2; 0} (thỏa).

Vậy m ∈ {−2; 0} thì hệ phương trình có nghiệm duy nhất nguyên.

Câu 4:

Cho ∆ABC nhọn nội tiếp đường tròn (O) với AB < AC. Các đường cao BE và CF của ∆ABC cắt nhau tại H.

1) Chứng minh tứ giác BCEF nội tiếp.

2) Chứng minh OA ⊥ EF.

3) Gọi M là trung điểm của BC, S là giao điểm của đường thẳng EF và BC. Kẻ đường kính AK của đường tròn (O). Chứng minh H, M, K thẳng hàng và chứng minh SH ⊥ AM.

Xem đáp án

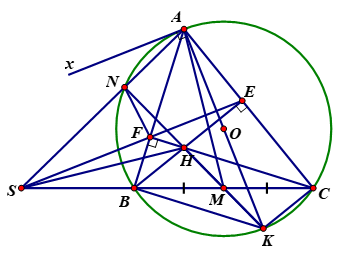
Cho ∆ABC nhọn nội tiếp đường tròn (O) với AB < AC. Các đườ (ảnh 1)

) Ta có $\hat{B F C} = 90 °$ (CF ⊥ AB)

$\hat{B E C} = 90 °$ (BE ⊥ AC)

Xét tứ giác BFEC có $\hat{B F C} = \hat{B E C} = 90 °$

Suy ra tứ giác BFEC nội tiếp.

2) Từ A kẻ tiếp tuyến Ax của (O)

Ta có $\hat{x A B} = \hat{A C B}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AB)

Mà $\hat{A C B} = \hat{A F E}$ (tứ giác FECB nội tiếp)

Suy ra $\hat{x A B} = \hat{A F E \Rightarrow}$ Ax // FE (hai góc so le trong)

Mà Ax ⊥ AO (Ax là tiếp tuyến của (O))

Suy ra FE ⊥ OA (điều phải chứng minh)

3) Ta có: $\hat{A C K} = 90 °$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow B K ⊥ A B$

$\hat{A B K} = 90 °$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow B K ⊥ A B$

Xét tứ giác BHCK có:

BH // CK (cúng vuông góc AC)

CH // BK (cùng vuông góc AB)

Suy ra tứ giác BHCK là hình bình hành

Tứ giác BHCK là hình bình hành có M là trung điểm BC

Suy ra M cũng là trung điểm HK suy ra M, H, K thẳng hàng

SA cắt đường tròn (O) tại N

Xét tứ giác nội tiếp BFEC có FE cắt BC tại S

Xét ∆SFB và ∆SCE có:

$\hat{E S C}$ là góc chung

$\hat{S F B} = \hat{S C E}$ (tứ giác BFEC nội tiếp)

Suy ra ∆SFB ∆SCE (g.g)

Suy ra $\frac{S F}{S C} = \frac{S B}{S E} \Leftrightarrow S F . S E = S B . S C$

Tương tự tứ giác BNAC nội tiếp (O) có AN cắt CB tại S.

Suy ra SN.SA = SB.SC

Từ 2 điều trên suy ra SN.SA = SF.SE

Xét ∆SNF và ∆SEA có:

$\hat{A S E}$ là góc chung

$\frac{S N}{S E} = \frac{S F}{S A}$ (chứng minh trên)

Do đó ∆SNF ∆SEA (c.g.c)

Suy ra $\hat{S N F} = \hat{S E A}$ .

Suy ra tứ giác ANFE nội tiếp (1)

Ta có $\hat{A F H} = 90 °$ (CF ⊥ AB)

$\hat{A E H} = 90 °$ (BE ⊥ AC)

Xét tứ giác AFHE có $\hat{A F H} + \hat{A E H} = 90 ° + 90 ° = 180 °$

Suy ra tứ giác AFHE nội tiếp. (2)

Từ (1) và (2) suy ra A, N, F, H, E nội tiếp cùng một đường tròn.

Có $\hat{A E H} = 90 °$ (BE ⊥ AC) AH là đường kính .

Suy ra $\hat{A N H} = 90 °$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow N H ⊥ S A$ .

Ta có $\hat{K N A} = 90 °$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow K N ⊥ S A$ .

Mà NH ⊥ SA (cmt).

Suy ra K, H, N thẳng hàng hay 4 điểm K, M, H, N thẳng hàng.

Suy ra MH ⊥ SA.

Xét tam giác ABC có H là giao điểm của 2 đường cao CF và BE.

Suy ra AH là dường cao thứ ba suy ra AH ⊥ BC hay AH ⊥ SM.

Xét tam giác ASM có:

MH ^ SA (cmt);

AH ^ SM (cmt).

Suy ra H là trực tâm của tam giác ASM.

Vậy SH ⊥ AM (điều phải chứng minh).

Câu 5:

Cho 1 ≤ x, y, z ≤ 2 và x² + y² + z² = 6. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $S = \sqrt{4 - x^{2}} + \sqrt{4 - y^{2}} + \sqrt{4 - z^{2}}$ .

Xem đáp án

Áp dụng bất đẳng thức Bunhiacopxki, ta có:

Xét S² = ${(1. \sqrt{4 - x^{2}} + 1. \sqrt{4 - y^{2}} + 1. \sqrt{4 - z^{2}})}^{2}$

$\leq^{B u n h i a} (1^{2} + 1^{2} + 1^{2}) ({\sqrt{4 - x^{2}}}^{2} + {\sqrt{4 - y^{2}}}^{2} + {\sqrt{4 - z^{2}}}^{2}) \leq^{B u n h i a} (1^{2} + 1^{2} + 1^{2}) ({\sqrt{4 - x^{2}}}^{2} + {\sqrt{4 - y^{2}}}^{2} + {\sqrt{4 - z^{2}}}^{2}) = 3. [4 + 4 + 4 - (x^{2} + y^{2} + z^{2})] = 3. (12 - 6) = 18 \Rightarrow S \leq \sqrt{18} = 3 \sqrt{2}$

Vậy Max S $= 3 \sqrt{2}$

Dấu bằng xảy khi $\frac{\sqrt{4 - x^{2}}}{1} = \frac{\sqrt{4 - y^{2}}}{1} = \frac{\sqrt{4 - z^{2}}}{1} \Leftrightarrow x = y = z$ .

Mà x² + y² + z² = 6 nên x = y = z = $\sqrt{2}$ .

Do 1 ≤ x ≤ 2 Û 1 ≤ x² ≤ 4 Û 3 ≥ 4 – x² ≥ 0 .

Tương tự ta có: $1 \geq \frac{4 - y^{2}}{3} \geq 0, 1 \geq \frac{4 - z^{2}}{3} \geq 0$ , .

Áp dụng tính chất: 0 ≤ a ≤ 1 thì $\sqrt{a} \geq a$ .

Ta có: $S = \sqrt{3} (\sqrt{\frac{4 - x^{2}}{3}} + \sqrt{\frac{4 - y^{2}}{3}} + \sqrt{\frac{4 - z^{2}}{3}})$

$\geq \sqrt{3} (\frac{4 - x^{2}}{3} + \frac{4 - y^{2}}{3} + \frac{4 - z^{2}}{3}) = \sqrt{3} (\frac{12 - (x^{2} + y^{2} + z^{2})}{3}) = 2 \sqrt{3}$

Vậy Min S = $2 \sqrt{3}$ khi (a; b; c) là hoán vị (2; 1; 1).

Bắt đầu thi ngay