5 câu hỏi trắc nghiệm thuộc Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 11

Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40

Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 11

14295 lượt thi
5 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải hệ phương trình sau:

a) ${\begin{cases} 4 x + 7 y = 16 \\ 4 x - 3 y = - 24 \end{cases}$

b) ${\begin{cases} 2 \sqrt{x - 2} + \sqrt{y + 3} = 4 \\ 3 \sqrt{x - 2} - 2 \sqrt{y + 3} = - 1 \end{cases}$

Xem đáp án

a) ${\begin{cases} 4 x + 7 y = 16 \\ 4 x - 3 y = - 24 \end{cases}$

$\Leftrightarrow {\begin{cases} 4 x + 7 y - (4 x - 3 y) = 16 - (- 24) \\ x = \frac{1}{4} (3 y - 24) \end{cases}$

$\Leftrightarrow {\begin{cases} 10 y = 40 \\ x = \frac{1}{4} (3 y - 24) \end{cases}$

$\Leftrightarrow {\begin{cases} y = 4 \\ x = - 3 \end{cases}$

Vậy hệ phương trình đã cho có cặp nghiệm là (−3; 4).

b) ${\begin{cases} 2 \sqrt{x - 2} + \sqrt{y + 3} = 4 \\ 3 \sqrt{x - 2} - 2 \sqrt{y + 3} = - 1 \end{cases}$

Điều kiện xác định ${\begin{cases} x - 2 \geq 0 \\ y + 3 \geq 0 \end{cases} \Leftrightarrow {\begin{cases} x \geq 2 \\ y \geq - 3 \end{cases}$

Đặt $a = \sqrt{x - 2}$ , $b = \sqrt{y + 3}$ (a ≥ 0, b ≥ 0).

Khi đó, hệ phương trình đã cho trở thành:

${\begin{cases} 2 a + b = 4 \\ 3 a - 2 b = - 1 \end{cases}$

$\Leftrightarrow {\begin{cases} b = 4 - 2 a \\ 3 a - 2 b + 2 (2 a + b) = - 1 + 2 . 4 \end{cases}$

$\Leftrightarrow {\begin{cases} b = 4 - 2 a \\ 7 a = 7 \end{cases}$

$\Leftrightarrow {\begin{cases} b = 2 \\ a = 1 \end{cases}$ (thỏa mãn)

Do đó

${\begin{cases} \sqrt{y + 3} = 2 \\ \sqrt{x - 2} = 1 \end{cases} \Leftrightarrow {\begin{cases} y + 3 = 4 \\ x - 2 = 1 \end{cases}$

$\Leftrightarrow {\begin{cases} y = 1 \\ x = 3 \end{cases}$ (thỏa mãn)

Vậy hệ phương trình đã cho có cặp nghiệm là (3; 1).

Câu 2:

Cho hàm số y = mx² có đồ thị là parabol (P) và đường thẳng (d): y = 3x + 4.

a) Tìm giá trị của m, biết (P) đi qua điểm M(1; 1). Vẽ (P) trên mặt phẳng tọa độ Oxy với giá trị của m vừa tìm được.

b) Với giá trị nào của m tìm được ở câu a, tìm tọa độ các giao điểm của (d) và (P).

Xem đáp án

a) Do (P) đi qua M nên thay giá trị của M(1; 1) vào hàm số y = mx² ta được

1 = m.1² $\Leftrightarrow$ m = 1

Vậy (P): y = x²

Bảng giá trị:

x	−2	−1	0	1	2
y = x²	4	1	0	1	4

Do đó (P) đi qua các điểm (−2; 4); (−1; 1); (0; 0); (1; 1); (2; 4).

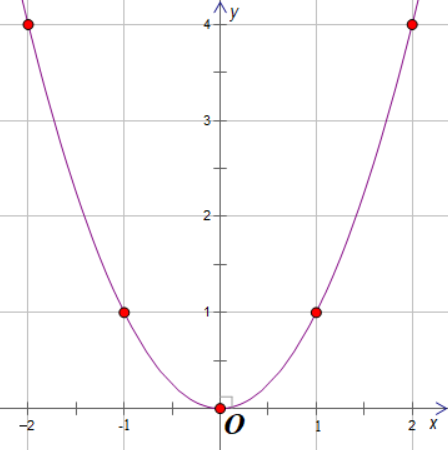
b) Phương trình hoành độ giao điểm của (P) và (d) là:

x² = 3x + 4

Û x² − 3x – 4 = 0

Û x² + x – 4x – 4 = 0

Û x(x + 1) – 4(x + 1) = 0

Û (x – 4)(x + 1) = 0

Û $[\begin{array}{l} x = 4 \\ x = - 1 \end{array}$

• Với x = 4 thì y = 3x + 4 = 3.4 + 4 = 16.

Do đó, ta có tọa độ giao điểm của (P) và (d) là A(4; 16).

• Với x = –1 thì y = 3x + 4 = 3.(–1) + 4 = 1.

Do đó, ta có tọa độ giao điểm của (P) và (d) là B(−1; 1).

Vậy tọa độ các giao điểm của (d) và (P) là A(4; 16) và B(−1; 1).

Câu 3:

Theo kế hoạch, hai tổ công nhân được giao sản xuất 5000 chiếc khẩu trang kháng khuẩn trong thời gian đã định. Do nhu cầu khẩu trang trong mùa dịch Covid tăng cao nên tổ I đã sản xuất vượt mước 50% và tổ II sản xuất vượt mức 40% so với kế hoạch. Vì vậy trong thời gian quy định hai tổ đã sản xuất được 7200 chiếc khẩu trang kháng khuẩn. Tính số khẩu trang kháng khuẩn được giao của mỗi tổ theo kế hoạch.

Xem đáp án

Gọi x (chiếc) là số khẩu trang tổ I được giao theo kế hoạch ( $x \in ℕ *$ , x < 5000)

Gọi y (chiếc) là số khẩu trang tổ II được giao theo kế hoạch ( $y \in ℕ *$ , y < 5000)

Do hai tổ công nhân được giao sản xuất 5000 chiếc khẩu trang nên:

x + y = 5000 (1)

Số khẩu trang tổ I sản xuất là: x + 50%.x = 1,5x (chiếc)

Số khẩu trang tổ II sản xuất là: y + 40%.y = 1,4y (chiếc)

Do hai tổ đã sản xuất được 7200 chiếc khẩu trang nên ta có:

1,5x + 1,4y = 7200 (2)

Từ (1) và (2) ta có hệ phương trình:

${\begin{cases} x + y = 5000 \\ 1,5 x + 1,4 y = 7200 \end{cases}$

$\Leftrightarrow {\begin{cases} y = 5000 - x \\ 1,5 x + 1,4 (5000 - x) = 7200 \end{cases}$

$\Leftrightarrow {\begin{cases} y = 5000 - x \\ 1,5 x + 7000 - 1,4 x = 7200 \end{cases}$

$\Leftrightarrow {\begin{cases} y = 5000 - x \\ 0,1 x = 7200 - 7000 \end{cases}$

$\Leftrightarrow {\begin{cases} y = 5000 - x \\ 0,1 x = 200 \end{cases}$

$\Leftrightarrow {\begin{cases} x = 2000 \\ y = 3000 \end{cases}$ (thỏa mãn)

Vậy tổ I được giao 2000 chiếc khẩu trang, tổ II được giao 3000 chiếc khẩu trang.

Câu 4:

Cho đường tròn (O; R). Từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là hai tiếp điểm). Từ B kẻ đường thẳng song song với AC cắt (O) tại D (D khác B), đường thẳng AD cắt (O) tại E (E khác D).

a) Chứng minh tứ giác ABOC nội tiếp.

b) Chứng minh AE.AD = AB².

c) Giả sử OA = 2R. Tính số đo góc BEC và diện tích tứ giác ABOC.

Xem đáp án

a) Ta có $\hat{O B A}$ = 90° (AB là tiếp tuyến của (O))

$\hat{O C A}$ = 90° (AC là tiếp tuyến của (O))

Xét tứ giác ABOC có $\hat{O B A}$ + $\hat{O C A}$ = 90° + 90° = 180°

Do đó tứ giác ABOC nội tiếp.

b) Xét ∆ABE và ∆ADB có:

$\hat{B A D}$ là góc chung

$\hat{B D A} = \hat{E B A}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung BE)

Suy ra ∆ABE đồng dạng ∆ADB (g.g)

Từ đó suy ra $\frac{A B}{A D} = \frac{A E}{A B} \Leftrightarrow A B^{2} = A D . A E$ (điều phải chứng minh)

c) Xét ∆OBA và ∆OCA có:

OA = OB = R

AB = AC (tính chất hai tiếp tuyến cắt nhau).

AO là cạnh chung

Suy ra ∆OBA = ∆OCA (c.c.c)

Xét ∆AOB vuông tại B có AO = 2R, OB = R.

Suy ra AB = $\sqrt{O A^{2} - O B^{2}} = \sqrt{4 R^{2} - R {}^{2}} = \sqrt{3} R$

Ta có cos( $\hat{B O A}$ ) $= \frac{O B}{O A} = \frac{R}{2 R} = \frac{1}{2}$ .

Suy ra $\hat{B O A} = 60 °$ .

S_AOB= $\frac{1}{2} A B . O B = \frac{1}{2} . R . \sqrt{3} R = \frac{\sqrt{3}}{2} R^{2}$

S_ABOC = S_AOB + S_AOC = 2S_AOB = $2. \frac{\sqrt{3}}{2} R^{2} = \sqrt{3} R^{2}$

Ta có: OA là phân giác của góc $\hat{B O C}$ (tính chất hai tiếp tuyến cắt nhau)

Suy ra $\hat{B O C} = 2 . \hat{B O A} = 2.60 ° = 120 °$

Khi đó,

Số đo $\overset{⌢}{B C}$ nhỏ = $\hat{B O C} = 120 °$ .

Số đo $\overset{⌢}{B C}$ lớn = 360° − số đo $\overset{⌢}{B C}$ nhỏ = 360° −120° = 240°.

$\Rightarrow \hat{B E C} = \frac{1}{2}$ số đo $\overset{⌢}{B C}$ lớn $= \frac{1}{2} . 240 ° = 120 °$

Câu 5:

Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức y = $\frac{x}{x^{2} + 1}$ .

Xem đáp án

Ta có $y = \frac{x}{x^{2} + 1}$

$\Rightarrow y - 0,5 = \frac{x}{x^{2} + 1} - 0,5$

$= \frac{- 0,5 (x^{2} - 2 x + 1)}{x^{2} + 1}$ $= - 0,5. \frac{{(x - 1)}^{2}}{x^{2} + 1} \leq 0$ với mọi x

$\Rightarrow$ y ≤ 0,5 với mọi x.

Ta lại có:

$\Rightarrow y + 0,5 = \frac{x}{x^{2} + 1} + 0,5$

$= \frac{0,5 (x^{2} + 2 x + 1)}{x^{2} + 1}$

$= 0,5. \frac{{(x + 1)}^{2}}{x^{2} + 1} \geq 0$ với mọi x

$\Rightarrow$ y ≥ −0,5 với mọi x.

Vậy giá trị lớn nhất của y là 0,5 và giá trị nhỏ nhất của y là −0,5.

Bắt đầu thi ngay