- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 15
-
15431 lượt thi
-
18 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 2:
Hệ phương trình có nghiệm (x; y) = (2; 0) khi giá trị của a là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thay x = 2; y = 0 vào phương trình ax + y = 6, ta được:
a.2 + 0 = 6 Û a = 3
Câu 3:
Trong các hàm số sau, hàm số nào đồng biến khi x < 0?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hàm số y = ax2 đồng biến khi x < 0 và a < 0.
Do đó hàm số y = −x2 khi x < 0 và a = −1 < 0 thì hàm số đồng biến.
Câu 4:
Với giá trị nào của a thì đồ thị hàm số y = ax2 đi qua điểm có tọa độ (2; 4)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Thay giá trị của điểm có tọa độ (2; 4) vào đồ thị hàm số y = ax2, ta được:
4 = a.22 Û a = 1.
Câu 5:
Trong các phương trình dưới đây, phương trình nào không phải là phương trình bậc hai một ẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phương trình bậc hai một ẩn là phương trình có dạng ax2 + bx + c = 0 (a ≠ 0)
Đáp án D có a = 0 nên không phải phương trình bậc hai một ẩn.
Câu 7:
Với giá trị nào của m thì phương trình x2 + mx + 9 = 0 có nghiệm kép:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: Δ = m2 – 4.1.9 = m2 – 36
Để phương trình có nghiệm kép thì Δ = 0 hay m2 – 36 = 0
Û (m – 6)(m + 6) = 0
Vậy m = 6 hoặc m = −6 thì phương trình đã cho có nghiệm kép.
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: R1 + R2 = 3 + 4 = 7 = OO’.
Vậy hai đường tròn này tiếp xúc ngoài.
Câu 9:
Cho hình vuông ABCD nội tiếp đường tròn (O). Số đo cung AB nhỏ là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Do hình vuông ABCD nội tiếp đường tròn (O).
Nên O là giao điểm của 2 đường chéo AC và BD.
Ta cũng có AC ⊥ BD do ABCD là hình vuông.
Suy ra = 90°.
Số đo cung AB nhỏ = = 90°.
Câu 10:
Tam giác ABC nội tiếp đường tròn đường kính BC biết AB = 3cm, AC = 4cm.
So sánh các cung nhỏ, ta được:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có BC là đường kính suy ra (góc nội tiếp chắn nửa đường tròn)
Xét ∆ABC vuông tại A, áp dụng định lý Pytago
BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25 = 52.
Suy ra BC = 5cm.
Khi đó BC > AC > AB (5 cm > 4 cm > 3 cm).
Do đó .
Câu 11:
Mệnh đề nào sau đây là sai?
Trong một đường tròn thì:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Mệnh đề đúng là:
Góc nội tiếp có số đo bằng nửa số đo của góc ở tâm “cùng chắn một cung”.
Câu 12:
Lấy A, B thuộc đường tròn (O) sao cho góc AOB bằng 80°. Số đo của góc nhọn tạo bởi tiếp tuyến tại A và dây AB của (O) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Số đo của góc nhọn tạo bởi tiếp tuyến tại A và dây AB của (O) bằng:
.
Câu 13:
Hai dây AB và CD của đường tròn (O) cắt nhau tại I, biết số đo các cung nhỏ AD và cung BC lần lượt là 40° và 60°. Số đo của góc BIC là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có góc BIC là góc có đỉnh nằm trong đường tròn nên ta có:
(sđ + sđ)
Câu 14:
Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M, biết = 60°. Số đo cung AB nhỏ và số đo cung AB lớn lần lượt là:
 Xem đáp án
Xem đáp án

Số đo cung AB lớn = 360° – số đo
cung AB nhỏ = 360° – 120° = 240°.
Câu 15:
Trong các tứ giác sau, tứ giác nào không nội tiếp được một đường tròn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hình vuông và hình chữ nhật đều có tổng hai góc đối bằng 90° + 90° = 180° nên nội tiếp đường tròn
Hình thang cân ta có góc đáy trên cộng góc đáy dưới bằng 180° ( trong cùng phía)
Mà hai góc ở đáy bằng nhau nên ta cũng có tổng hai góc đối bằng 180°
Câu 16:
a) Giải hệ phương trình:
b) Giải bài toán bằng cách lập hệ phương trình: Một hình chữ nhật có chiều dài hơn chiều rộng 5m, chu vi bằng 50m. Tính các kích thước của hình chữ nhật đó.
 Xem đáp án
Xem đáp án
a)
Vậy hệ phương trình có cặp nghiệm là (3; 1)
b) Gọi x (m) và y (m) lần lượt là chiều dài và chiều rộng của hình chữ nhật
(25 > x > y > 0).
Ta có nữa chu vi của hình chữ nhật là: x + y = (1)
Vì chiều dài hơn chiều rộng 5m ta có: x – y = 5 (2)
Từ (1) và (2) ta có hệ phương trình:
(thỏa mãn)
Vậy hình chữ nhật đã cho có chiều dài là 15 m và chiều rộng 10 m.
Câu 17:
a) Vẽ đồ thị hai hàm số y = x2 và y = − x + 2 trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của hai đồ thị đó bằng phép tính.
 Xem đáp án
Xem đáp án
) Vẽ y = x2
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Vẽ y = −x + 2 có a = −1 b = 2.
Hàm số qua 2 điểm (0; b) = (0; 2) và = (2; 0).
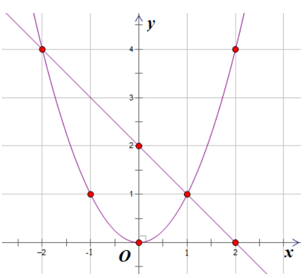
b) Phương trình hoành độ giao điểm của của hai đồ thị là:
x2 = –x + 2
Û x2 + x – 2 = 0
Û x2 + 2x – x – 2 = 0
Û x( x + 2) – (x + 2) = 0
Û (x – 1)(x + 2) = 0
Û
• Với x = 1 thì y = –x + 2 = –1 + 2 = 1.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(1; 1).
• Với x = –2 thì y = –x + 2 = – (–2) + 2 = 4.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(−2; 4).
Vậy hai đồ thị hàm số trên có hai giao điểm là A(1; 1) và B(−2; 4).
Câu 18:
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P. Chứng minh rằng:
a) Tứ giác BFHD nội tiếp.
b) FP.FC = FA.FB
c) Vẽ đường kính AI. Chứng minh H và I đối xứng với nhau qua trung điểm của BC.
 Xem đáp án
Xem đáp án
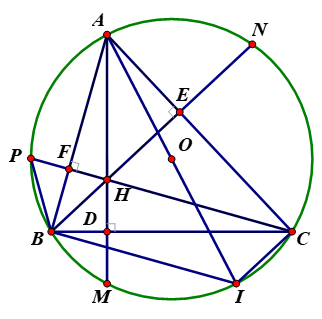


CI // BH (cùng vuông góc AC)
Suy ra tứ giác BHCI là hình bình hành.
Suy ra BC cắt HI tại trung điểm mỗi đường.
Suy ra H và I đối xứng với nhau qua trung điểm của BC.


