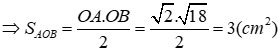- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Đề kiểm tra giữa học kì 2 môn Toán 9 (Mới nhất)_đề 26
-
14293 lượt thi
-
5 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho hai biểu thức :
và 
với 
1) Tính giá trị của biểu thức B khi 
2) Rút gọn biểu thức M = A.B
3) Tìm giá trị lớn nhất của biểu thức M
Xem đáp án
\(\begin{array}{l}1)x = \frac{9}{{16}}(tm) \Rightarrow B = \frac{{\sqrt {\frac{9}{{16}}} - 3}}{2} = \frac{{ - 9}}{8}\\2)M = A.B = \left( {\frac{1}{{\sqrt x - 3}} + \frac{{\sqrt x + 11}}{{x - 9}}} \right).\frac{{\sqrt x - 3}}{2}\left( \begin{array}{l}x \ge 0\\x \ne 9\end{array} \right)\\ = \frac{{\sqrt x + 3 + \sqrt x + 11}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}.\frac{{\sqrt x - 3}}{2} = \frac{{2\left( {\sqrt x + 7} \right)}}{{2\left( {\sqrt x + 3} \right)}} = \frac{{\sqrt x + 7}}{{\sqrt x + 3}}\end{array}\)
\(3)M = 1 + \frac{4}{{\sqrt x + 3}}\)
Vì \(\sqrt x \ge 0 \Rightarrow \sqrt x + 3 \ge 3 \Rightarrow M \le 1 + \frac{4}{3} = \frac{7}{3}\)
Vậy \(Max\,M = \frac{7}{3} \Leftrightarrow x = 0\)
Câu 2:
Giải bài toán bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào một bể không có nước thì sau 12 giờ sẽ đầy bể.Nếu mở vòi I chảy trong 4 giờ rồi khóa lại và mở tiếp vòi II chảy trong 3 giờ thì được 
bể. Hỏi nếu mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể ?
Xem đáp án
Gọi \(x,y\)là số giờ vòi 1, vòi 2 chảy một mình đầy bể \(\left( {x > 12,y > 12} \right)\)
Theo bài ta có hệ :
\(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{{12}}\\\frac{4}{x} + \frac{3}{y} = \frac{3}{{10}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 20\\y = 30\end{array} \right.(tm)\)
Vậy vòi 1: 20 giờ, vòi 2: 30 giờ
Câu 3:
1) Cho hệ phương trình :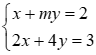 
a) Giải hệ phương trình khi m = 3
b) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn điều kiện x và y là hai số đối nhau .
2) Cho hàm số 
có đồ thị là parabol (P) và hàm số y = x - 2 có đồ thị là đường thẳng (d). Gọi A và B là giao điểm của (d) với (P). Tính diện tích tam giác OAB.
Xem đáp án
1) a) Khi \(m = 3 \Rightarrow \left\{ \begin{array}{l}x + 3y = 2\\2x + 4y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{1}{2}\end{array} \right.\)
\(b)\left\{ \begin{array}{l}x + my = 2\\2x + 4y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 2my = 4\\2x + 4y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{1}{{2m - 4}}\\x = \frac{{3 - \frac{2}{{m - 2}}}}{2} = \frac{{2\left( {3m - 8} \right)}}{{m - 2}}\end{array} \right.\)
Để \(x,y\)đối nhau thì :
\( \Rightarrow \frac{{2\left( {3m - 8} \right)}}{{m - 2}} = \frac{{ - 1}}{{2m - 4}} \Leftrightarrow \left( {6m - 16} \right).2 = - 1 \Leftrightarrow 12m = 31 \Leftrightarrow m = \frac{{31}}{{12}}\)
2) Hoành độ \(A,B\)là nghiệm hệ \( - {x^2} = x - 2 \Leftrightarrow {x^2} + x - 2 = 0\)
\( \Rightarrow \left[ \begin{array}{l}{x_A} = 1 \Rightarrow {y_A} = - 1\\{x_B} = - 2 \Rightarrow {y_B} = - 4\end{array} \right. \Rightarrow A\left( {1; - 1} \right);B\left( { - 2; - 4} \right),O\left( {0;0} \right)\)
vuông tại A
