Cho hai biểu thức :
và 
với 
1) Tính giá trị của biểu thức B khi 
2) Rút gọn biểu thức M = A.B
3) Tìm giá trị lớn nhất của biểu thức M
Giải bởi Vietjack
\(\begin{array}{l}1)x = \frac{9}{{16}}(tm) \Rightarrow B = \frac{{\sqrt {\frac{9}{{16}}} - 3}}{2} = \frac{{ - 9}}{8}\\2)M = A.B = \left( {\frac{1}{{\sqrt x - 3}} + \frac{{\sqrt x + 11}}{{x - 9}}} \right).\frac{{\sqrt x - 3}}{2}\left( \begin{array}{l}x \ge 0\\x \ne 9\end{array} \right)\\ = \frac{{\sqrt x + 3 + \sqrt x + 11}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}.\frac{{\sqrt x - 3}}{2} = \frac{{2\left( {\sqrt x + 7} \right)}}{{2\left( {\sqrt x + 3} \right)}} = \frac{{\sqrt x + 7}}{{\sqrt x + 3}}\end{array}\)
\(3)M = 1 + \frac{4}{{\sqrt x + 3}}\)
Vì \(\sqrt x \ge 0 \Rightarrow \sqrt x + 3 \ge 3 \Rightarrow M \le 1 + \frac{4}{3} = \frac{7}{3}\)
Vậy \(Max\,M = \frac{7}{3} \Leftrightarrow x = 0\)
1) Cho hệ phương trình :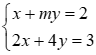 
a) Giải hệ phương trình khi m = 3
b) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn điều kiện x và y là hai số đối nhau .
2) Cho hàm số 
có đồ thị là parabol (P) và hàm số y = x - 2 có đồ thị là đường thẳng (d). Gọi A và B là giao điểm của (d) với (P). Tính diện tích tam giác OAB.
Giải bài toán bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào một bể không có nước thì sau 12 giờ sẽ đầy bể.Nếu mở vòi I chảy trong 4 giờ rồi khóa lại và mở tiếp vòi II chảy trong 3 giờ thì được 
bể. Hỏi nếu mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể ?
Cho nữa đường tròn (O), đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M( khác K, B).Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP // K. Gọi Q là giao điểm của các đường thẳng AP và BM; E là giao điểm của PB và AM.
1) Chứng minh rằng : Tứ giác PQME nội tiếp đường tròn.
2) Chứng minh: 
3) Chứng minh: AM.BE = AN.AQ
4) Gọi R, S lần lược là giao điểm thứ hai của QA, QB với đường tròn ngoại tiếp tam giác OMP. Chứng minh rằng khi Mdi động trên cung KB thì trung điểm I của RSluôn nằm trên một đường cố định
