- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
Đề kiểm tra giữa học kì 2 môn Toán 9 (Mới nhất)_đề 22
-
14510 lượt thi
-
4 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
1) Cho hàm số 
.Tìm a biết đồ thị hàm số đi qua điểm A(-1;1)
2) Giải các phương trình sau :
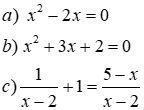
Xem đáp án
\(1)y = a{x^2}\)qua \(A\left( { - 1;1} \right) \Rightarrow {\left( { - 1} \right)^2}.a = 1 \Leftrightarrow a = 1\)
\(\begin{array}{l}2)a){x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\\b){x^2} + 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 2\end{array} \right.\\c)\frac{1}{{x - 2}} + 1 = \frac{{5 - x}}{{x - 2}}\left( {x \ne 2} \right) \Leftrightarrow \frac{{1 + x - 2}}{{x - 2}} = \frac{{5 - x}}{{x - 2}}\\ \Rightarrow x - 1 = 5 - x \Leftrightarrow x = 3(tm)\end{array}\)
Câu 2:
( Giải bài toán bằng cách lập hệ phương trình )
Một hình chữ nhật có chiều dài hơn chiều rộng 20m.Nếu gấp đôi chiều dài và gấp 3 lần chiều rộng thì chu vi của hình chữ nhật là 480m. Tính chiều dài và chiều rộng của hình chữ nhật đó.
Xem đáp án
Gọi \(x\)là chiều dài, \(y\)là chiều rộng \(\left( \begin{array}{l}x,y > 0\\x > 20\end{array} \right)\)
Theo bài ta có hệ : \(\left\{ \begin{array}{l}x - y = 20\\2x + 3y = 240\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 60\\y = 40\end{array} \right.(tm)\)
Vậy chiều dài : 60m, chiều rộng : 40m
Câu 3:
Cho phương trình 
1) Chứng minh rằng phương trinh luôn có hai nghiệm phân biệt với mọi giá trị của m.
2) Gọi 
là hai nghiệm của phương trình. Tìm m để 
Xem đáp án
\({x^2} - 2mx - 3 = 0\)
\(a)\Delta ' = {m^2} + 3 > 0\)nên phương trình luôn có hai nghiệm phân biệt
b) Áp dụng hệ thức Vi – et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = - 3\end{array} \right.\)
\(\begin{array}{l}x_1^2 + x_2^2 = 10 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow 2m + 6 = 10 \Leftrightarrow m = 2\end{array}\)
Câu 4:
Cho 
và đường thẳng 
Chứng minh rằng với mọi m parapol (P) và đường thẳng (d) luôn cắt nhau tai hai điểm phân biệt. Tìm m sao cho hai giao điểm đó có hoành độ dương.
Xem đáp án
Ta có phương trình hoành độ giao điểm \(\left( P \right),\left( d \right):\)
\({x^2} - 2\left( {m + 3} \right)x + 2m - 2 = 0\)
\(\Delta ' = {\left( {m + 3} \right)^2} - \left( {2m - 2} \right) = {m^2} + 4m + 11 > 0\)
Nên \(\left( d \right)\)cắt (P) tại hai điểm phân biệt
Do \({x_1} > 0,{x_2} > 0 \Rightarrow \left\{ \begin{array}{l}{x_1} + {x_2} > 0\\{x_1}{x_2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m + 6 > 0\\2m - 2 > 0\end{array} \right. \Leftrightarrow m > 1\)