Trên tập hợp số phức, xét phương trình $z^2-mz+m+8=0$  (m là tham số thực). Có bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm $z_1,z_2$  phân biệt thỏa mãn $\left|z_1\left(z_1^2+m{z}_2\right)\right|=\left(m^2-m-8\right)\left|z_2\right|$ ?

Gọi S là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các chữ số 1;2;3;4;5;6. Cho ngẫu nhiên một số từ S, tính xác suất để số được chọn là một số chia hết cho 5.

Gọi S là tập hợp tất cả các số phức z sao cho số phức $w=\frac{z+3i-1}{z+3+i}$  là số thuần ảo. Xét các số phức $z_1,z_2\in S$  thỏa mãn $\left|z_1-z_2\right|=2$ , giá trị lớn nhất của $P={\left|z_1-3i\right|}^2-{\left|z_2-3i\right|}^2$  bằng

Trong không gian với hệ trục tọa độ Oxyz, góc giữa hai mặt phẳng Oxy và Oxz bằng

Trong không gian Oxyz, cho đường thẳng $d:\frac{x-1}{2}=\frac{y+3}{-1}=\frac{z}{3}$ . Phương trình tham số của đường thẳng d là

Trong không gian Oxyz, cho mặt cầu (S) có phương trình $x^2+y^2+z^2-2x+4y-6z-2=0$ . Đường kính mặt cầu (S) là

Cho hình lăng trụ đứng ABC/A’B’C’ có đáy là tam giác ABC là tam giác vuông cân tại A, BC = a. Gọi M là trung điểm của cạnh AA’, biết hai mặt phẳng (MBC) và (MB’C’) vuông góc với nhau. Thể tích khối lăng trụ ABC.A’B’C’ bằng

Cho ${\text{log}}_{a}b=\mathrm{3,}{\text{\hspace{0.17em}log}}_{a}c=-4$ . Khi đó $P={\text{log}}_a\left(\frac{a^3\sqrt{c}}{b^2}\right)$  bằng bao nhiêu?

Cho hàm số $y=f\left(x\right)=a{x}^3+b{x}^2+cx+d$  có đồ thị như hình vẽ dưới đây.

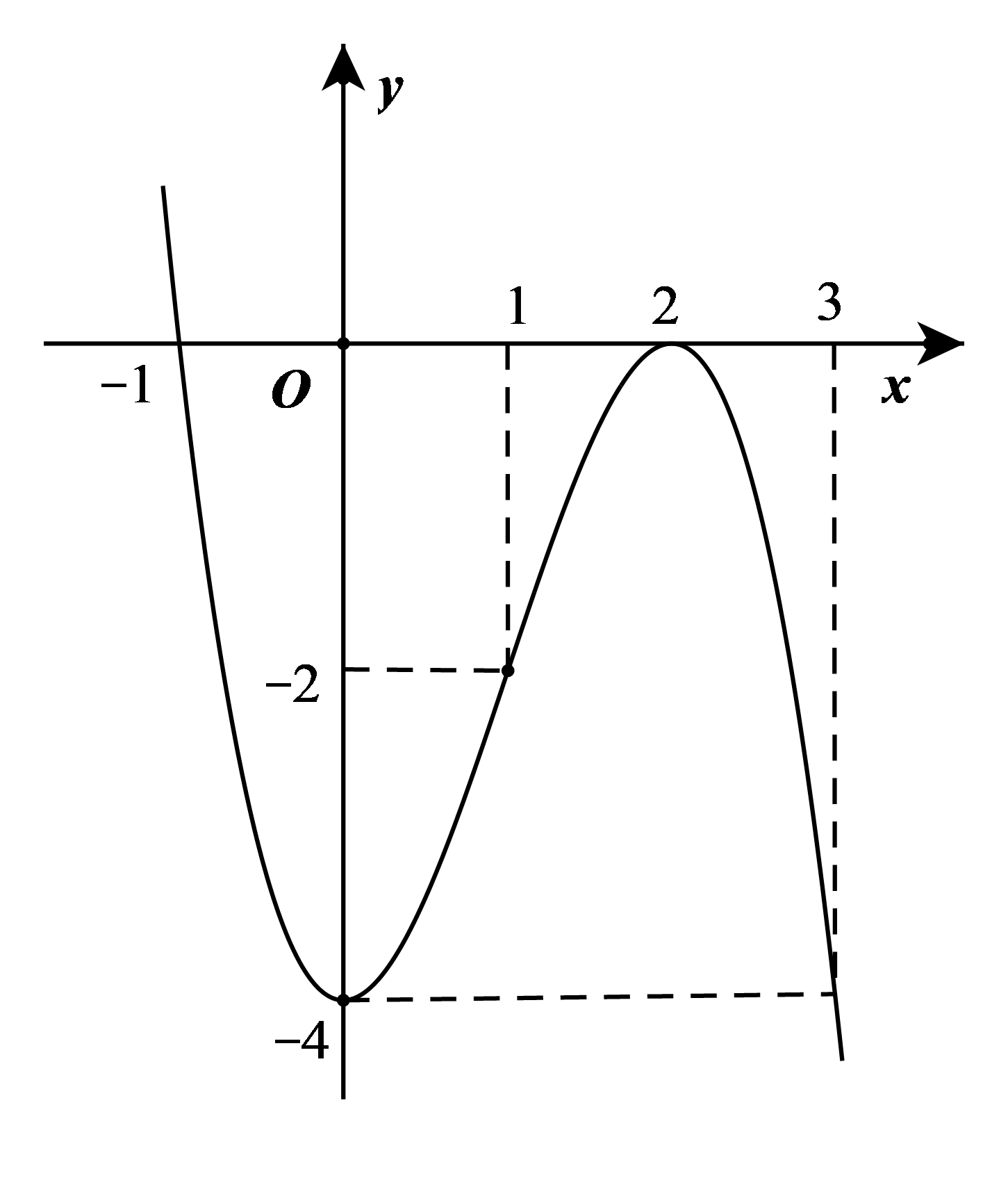
Hàm số y = f(x)  đồng biến trên khoảng nào?

Cho hàm số f(x) thỏa mãn $f\left(x\right)-x.f^{\text{'}}\left(x\right).\ln x=2x^2.f^2\left(x\right),\forall x\in \left(1;+\infty \right)$ . Biết $f\left(x\right)>\mathrm{0,}\forall x\in \left(1;+\infty \right)$  và $f\left(e\right)=\frac{1}{e^2}$ . Tính diện tích S của hình phẳng giới hạn bởi các đường $y=x.f\left(x\right),y=\mathrm{0,}x=e,x=e^2$ .

Có tất cả bao nhiêu cặp số nguyên dương (x;y) với $y\le 20$  thỏa mãn:

${\log }_{2023}\frac{x+1}{y+1}+x^2{y}^2+2x{y}^2\le \left(y+2\right)y^3$?

Nếu ${\int }_{-1}^{3}f\left(x\right)\text{\hspace{0.17em}d}x=-5$  và ${\int }_3^{5}f\left(x\right)\text{\hspace{0.17em}d}x=1$  thì ${\int }_{-1}^{5}f\left(x\right)\text{\hspace{0.17em}d}x$  bằng

Cho khối lăng trụ đứng có cạnh bên bằng 5, đáy là hình vuông có cạnh bằng 4. Thể tích khối lăng trụ bằng

Trong không gian Oxyz, cho điểm M(3;2;-1). Khi đó, điểm đối xứng với M qua mặt phẳng (yOz) có tọa độ bằng

Có bao nhiêu giá trị nguyên thuộc đoạn [-2023;2023] của tham số thực m để hàm số $y=\left|e^{3x}-3\left(m+2\right)e^{2x}+3m\left(m+4\right)e^x\right|$  đồng biến trên khoảng $\left(-\infty ;\ln 2\right)$ ?