Cho tam giác ABC nhọn, nội tiếp đường tròn (O;R) . Kẻ AH vuông góc với BC tại H, HK vuông góc với AB tại K và HI vuông góc với AC tại I.
a) Chứng minh tứ giác AKHI nội tiếp.
b) Gọi E là giao điếm của AH với KI Chứng minh rằng
c) Chứng minh KJ vuông góc với AO.
d) Giả sử điểm A và đường tròn (O;R) cố định, còn dây cung BC thay đổi sao cho Xác định vị trí của dây cung BC sao cho tam giác ABC có diện tích lớn nhất.
 Giải bởi Vietjack
Giải bởi Vietjack
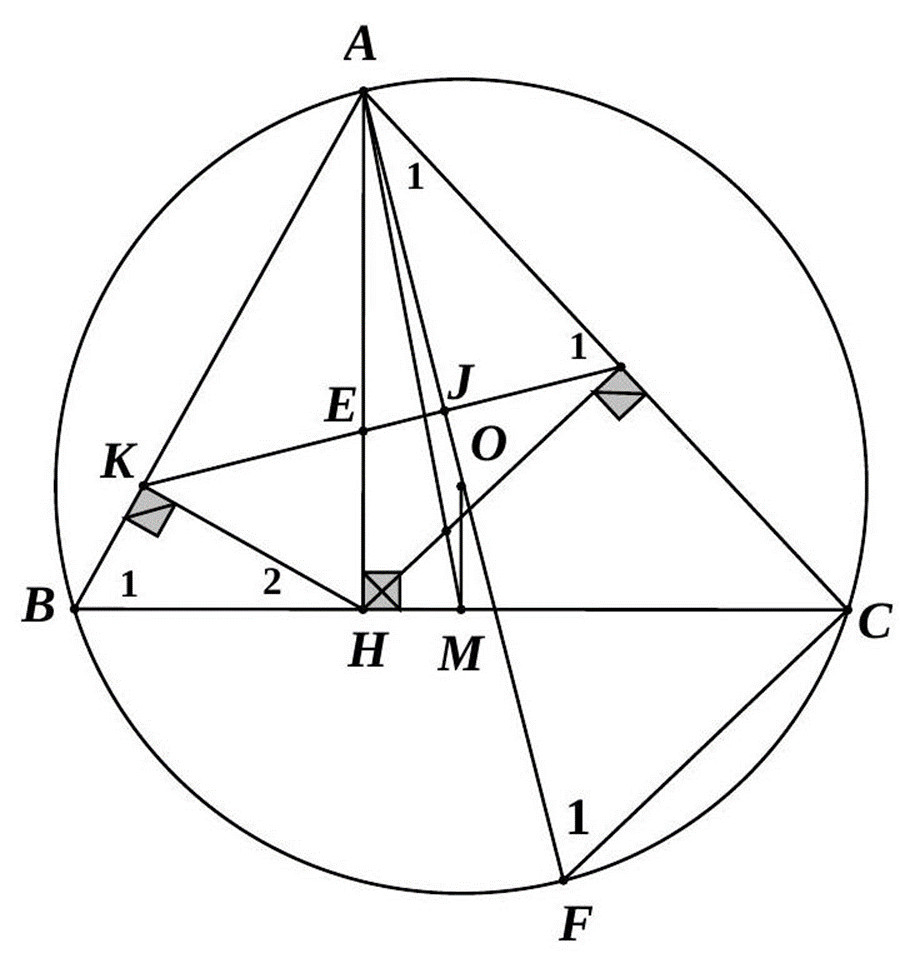
a) Ta có: (vì tại
(vì tại I)
Xét tứ giác AKHI có:
mà hai góc này ở vị trí đối nhau.
Vậy tứ giác AKHI nội tiếp đường tròn.
b) Vì tứ giác AKHI nội tiếp đường tròn (cmt) nên (hai góc nội tiếp cùng chắnHay
Xét và có: (hai góc đối đỉnh) và
Do đó: (g.g)
c) Kẻ đường kính AF của đường tròn (O;R); Gọi J là giao điểm của KI và AO.
Xét đường tròn (O;R) có (hai góc nội tiếp cùng chắn cung (1) ![]()
Lại có (vì cùng phụ với (2)
Vì tứ giác AKHI nội tiếp đường tròn (cmt)
nên (hai góc nội tiếp cùng chắn cung AK) (3)
Từ (1), (2) và (3) suy ra:
Mà trong đường tròn (O;R) có: (góc nội tiếp chắn nửa đường tròn).
Hay .
Từ (3) và (4) suy ra
Vậy KI vuông góc với AO.
d) Giả sử điểm A và đường tròn (O;R) cố định, còn dây BC thay đổi sao cho
Có (góc nội tiếp chắn nửa đường tròn).
(hai góc nội tiếp cùng chắn cung của đường tròn
Xét và có: và
Do đó: (g.g). Suy ra
Ta có:
Do R không đổi nên lớn nhất lớn nhất.
Gọi M là trung điểm của BC thì Do đó BC lớn nhất bé nhất.
Ta có
OM bé nhất bằng thẳng hàng và
Khi đó
Vậy diện tích lớn nhất khi BC cách A một khoảng bằng đều).
Một hình nón có diện tích đáy bằng và có chiều cao gấp ba lần bán kính đáy. Tính thể tích của hình nón đó.
Cho hệ phương trình (với m là tham số).
1) Giải hệ phương trình vời m = 2.
2) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn
Trong mặt phẳng tọa độ Oxyz cho parabol và đường thẳng (với m là tham số).
1) Tìn m để (d) đi qua điểm A (2;8).
2) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ thỏa mãn
Cho hai biểu thức và (với
1) Tính giá tri biểu thức Q với x = 4.
2) Chứng minh rằng
3) Tìm tất cả các giá trị của x để P nhận giá trị là các số nguyên.