Trong mặt phẳng tọa độ \[Oxy,\] gọi \(\left( H \right)\) là tập hợp các điểm biểu diễn hình học của số phức \(z\) thỏa mãn
D. \(8\pi - 4.\)
Giải bởi Vietjack
Gọi \[z = x + yi\,\, \Rightarrow \bar z = x - yi.\]
Ta có \[\left\{ {\begin{array}{*{20}{l}}{\left| {z + \bar z} \right| \ge 12}\\{\left| {z - 4 - 3i} \right| \le 2\sqrt 2 }\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2\left| x \right| \ge 12}\\{{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2} \le 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left| x \right| \ge 6}\\{{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2} \le 8}\end{array}\,\,\left( H \right)} \right.} \right.} \right..\]
Diện tích \(\left( H \right)\) là phần tô đậm trong hình vẽ.
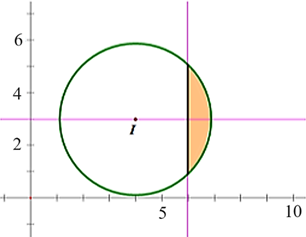
Giải hệ: \(\left\{ {\begin{array}{*{20}{l}}{y = 3}\\{{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2} = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 3}\\{x = 4 \pm 2\sqrt 2 }\end{array}} \right.} \right..\)
Suy ra đồ thị hàm số \(y = 3\) cắt đường tròn \((C)\) tại \(E\left( {4 - 2\sqrt 2 \,;\,\,3} \right)\) và \(F\left( {4 + 2\sqrt 2 \,;\,\,3} \right)\).
Vậy diện tích của hình phẳng \((H)\) là: \(2\int\limits_6^{4 + 2\sqrt 2 } {\left( {3 + \sqrt {8 - {{(x - 4)}^2}} - 3} \right)dx} = 2\pi - 4.\) Chọn C.
Số điểm biểu diễn nghiệm của phương trình \(\sin 4x\left( {2\cos x - \sqrt 2 } \right) = 0\) trên đường tròn lượng giác là
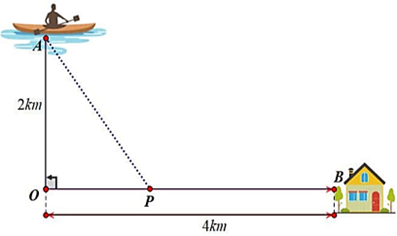
Bạn Hưng đang trên chiếc thuyền tại vị trí \[A\] cách bờ sông \(2\;\,{\rm{km}}\), bạn dự định chèo thuyền vào bờ và tiếp tục chạy bộ theo một đường thẳng để đến một địa điểm \({\rm{B}}\) tọa lạc ven bờ sông, \({\rm{B}}\) cách vị trí \[O\] trên bờ gần với thuyền nhất là \(4\;\,{\rm{km}}\) (hình vẽ). Biết rằng bạn Hưng chèo thuyền với vậntốc \(6\;\,{\rm{m}}/{\rm{h}}\) và chạy bộ trên bờ với vận tốc \(10\;\,{\rm{km}}/{\rm{h}}.\) Khoảng thời gian ngắn nhất để bạn Hưng từ vị trí xuất phát đến được điểm B là\[A\left( {1\,;\,\,1} \right),\,\,B\left( {4\,;\,\, - 3} \right).\]
Đọc đoạn trích sau đây và trả lời câu hỏi:
Nhà nước ba năm mở một khoa,
Trường Nam thi lẫn với trường Hà.
Lôi thôi sĩ tử vai đeo lọ,
Ậm oẹ quan trường miệng thét loa.
Lọng cắm rợp trời quan sứ đến
Váy lê quét đất mụ đầm ra.
Nhân tài đất Bắc nào ai đó?
Ngoảnh cổ mà trông cảnh nước nhà.
(Vịnh khoa thi hương – Trần Tế Xương)
Phong cách ngôn ngữ của văn bản là gì?
Tính đến đầu năm 2011, dân số toàn tỉnh Bình Phước đạt gần \[905\,\,300,\] mức tăng dân số là \[1,37\% \] mỗi năm. Tỉnh thực hiện tốt chủ trương \[100\% \] trẻ em đúng độ tuổi đều vào lớp 1. Đến năm học 2024 – 2025 ngành giáo dục của tỉnh cần chuẩn bị bao nhiêu phòng học cho học sinh lớp 1, mỗi phòng dành cho 35 học sinh? (Giả sử trong năm sinh của lứa học sinh vào lớp 1 đó toàn tỉnh có \[2\,\,400\] người chết, số trẻ tử vong trước 6 tuổi không đáng kể).
Cho hàm số \(f\left( x \right) = {x^3} - 6{x^2} + 9x + 2.\) Tìm tất cả các giá trị của tham số \(m\) sao cho bất phương trình \(f\left( {3x + 1} \right) + 9{x^2} - 6x + 1 \le m\) đúng với mọi \[x \in \left[ {0\,;\,1} \right]\]?
Cho hình lập phương \(ABCD \cdot A'B'C'D'\) có độ dài cạnh bằng 1. Gọi \[M,\,\,N,\,\,P,\,\,Q\] lần lượt là trung điểm của \(AB,\,\,BC,\,\,C'D',\,\,DD'.\) Gọi thể tích khối tứ diện \[MNPQ\] là phân số tối giản \(\frac{a}{b}\), với \(a,\,\,b \in {\mathbb{N}^*}.\) Tính \(a + b.\)
Đọc đoạn trích sau và trả lời câu hỏi:
Vũ Như Tô (đầy hi vọng) - Dẫn ta ra mắt An Hòa Hầu, để ta phân trần, để ta giảng giải, cho người đời biết rõ nguyện vọng của ta. Ta tội gì. Không, ta chỉ có một hoài bão là tô điểm cho đất nước, đem hết tài ra xây cho giống nòi một tòa đài hoa lệ, thách cả những công trình sau trước, tranh tinh xảo với hóa công. Vậy thì ta có tội gì? Ta xây Cửu Trùng Đài có phải đâu để hại nước? Không, không, Nguyễn Hoằng Dụ sẽ biết cho ta, ta không có tội và chủ tướng các ngươi sẽ cởi trói cho ta để ta xây nốt Cửu Trùng Đài, dựng một kì công muôn thuở…
(Vĩnh biệt Cửu Trùng Đài – Nguyễn Huy Tưởng)
Qua lời nói của nhân vật Vũ Như Tô, hình tượng Cửu Trùng Đài mang ý nghĩa gì?
Cho hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số \[a,\,\,b,\,\,c,\,\,d?\]
