Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 2)
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 2)
-
358 lượt thi
-
149 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Biểu đồ dưới đây thể hiện năng suất lúa của vùng đồng bằng sông Hồng, đồng bằng sông Cửu Long và cả nước qua các năm:
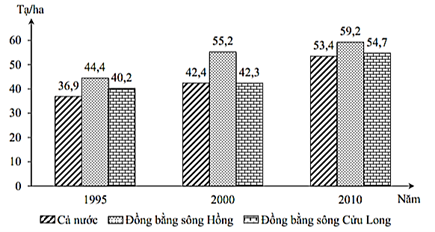
Trong năm 2000, năng suất của đồng bằng sông Hồng nhiều hơn năng suất lúa của đồng bằng sông Cửu Long là bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Câu 2:
Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\), góc giữa cạnh bên và mặt đáy bằng \(60^\circ .\) Thể tích khối chóp là
 Xem đáp án
Xem đáp án
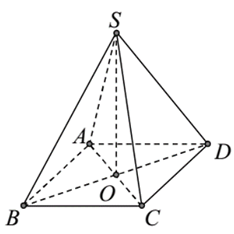
Giả sử hình chóp tứ giác đều là \[S.ABCD.\]
Gọi \[O\] là giao điểm của \[BD\] và \[AC.\]
Ta có \[SO \bot \left( {ABCD} \right),\,\,\widehat {SAO} = 60^\circ ,\,\,AC = a\sqrt 2 \Rightarrow OA = \frac{{a\sqrt 2 }}{2}.\]
Khi đó \(SO = AO \cdot \tan \widehat {SAO} = \frac{{a\sqrt 6 }}{2},\,\,{S_{ABCD}} = {a^2}.\)
Thể tích khối chóp là \(V = \frac{1}{3}SO \cdot {S_{ABCD}} = \frac{{{a^3}\sqrt 6 }}{6}.\) Chọn A.Câu 3:
 Xem đáp án
Xem đáp án
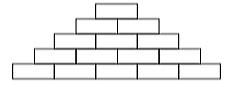
Theo bài ra, số viên gạch ở mỗi hàng lập thành 1 cấp số cộng.
Với \({u_1} = 1\) và công sai \(d = 1\), số hạng cuối là \({u_n} = 500.\)
Do đó \({u_n} = {u_1} + \left( {n - 1} \right)\,d \Leftrightarrow 500 = 1 + \left( {n - 1} \right).1 \Leftrightarrow n = 500.\)
Vậy tổng số viên gạch cần dùng là \({S_{500}} = \frac{{500 \cdot \left( {2 \cdot 1 + 499.1} \right)}}{2} = 125\,\,250.\)
Chọn D.
Câu 4:
Trong không gian với hệ tọa độ \[Oxyz,\] cho ba điểm \(M\left( {2\,;\,\,3\,;\,\, - 1} \right),\,\,N\left( { - 1\,;\,\,1\,;\,\,1} \right)\) và \(P\left( {1\,;\,\,m - 1\,;\,\,2} \right).\) Tìm \(m\) để tam giác \[MNP\] vuông tại \[N.\]
 Xem đáp án
Xem đáp án
Ta có \[\overrightarrow {NM} = \left( {3\,;\,\,2\,;\, - 2} \right),\overrightarrow {NP} = \left( {2\,;\,\,m - 2\,;\,\,1} \right)\].
Tam giác \[MNP\] vuông tại \(N\) khi và chỉ khi \(\overrightarrow {NM} \cdot \overrightarrow {NP} = 0 \Leftrightarrow 3 \cdot 2 + 2\left( {m - 2} \right) - 2 \cdot 1 = 0 \Leftrightarrow m = 0.\)
Vậy giá trị cần tìm của \(m\) là \(m = 0.\) Chọn B.
Câu 5:
Gọi \({z_1},\,\,{z_2},\,\,{z_3}\) là ba nghiệm của phương trình \({z^3} + {z^2} + 5z - 7 = 0.\) Tính \(M = \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right|\,?\)
 Xem đáp án
Xem đáp án
Ta có: \({z^3} + {z^2} + 5z - 7 = 0 \Leftrightarrow \left( {z - 1} \right)\left( {{z^2} + 2z + 7} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{z = 1}\\{z = - 1 + i\sqrt 6 }\\{z = - 1 - i\sqrt 6 }\end{array}} \right.\).
Suy ra: \(M = \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right| = \left| 1 \right| + \left| { - 1 + i\sqrt 6 } \right| + \left| { - 1 - i\sqrt 6 } \right| = 1 + 2\sqrt 7 .\)
Chọn A.
Câu 6:
 Xem đáp án
Xem đáp án
Gọi vị trí thấp nhất của ống bương là là vị trí của máng nước (như hình vẽ).
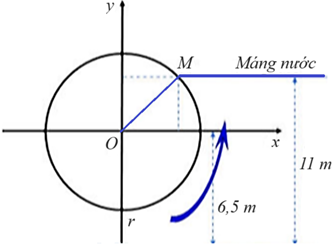
Tung độ của điểm \[M\] là \({y_M} = 11 - 6,5 = 4,5\)
\( \Rightarrow \sin \widehat {xOM} = \frac{{{y_M}}}{{OM}} = \frac{{4,5}}{5} = 0,9 \Rightarrow \widehat {xOM} \approx 64^\circ \).
Ta có \(\widehat {TOM} = \widehat {TOx} + \widehat {xOM} = 90^\circ + 64^\circ = 154^\circ .\)
Vì thời gian cọn nước thực hiện 1 vòng quay là 3 phút nên thời gian ống bương di chuyển từ \(T\)đến \(M\) là \(\frac{{3.154}}{{360}} = \frac{{77}}{{60}}\) (phút). Chọn C.
Câu 7:
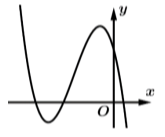
Cho hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ. Có bao nhiêu số dương trong các số \[a,\,\,b,\,\,c,\,\,d?\]
 Xem đáp án
Xem đáp án
Dựa vào hình vẽ, ta có:
Nét cuối đi xuống \( \Rightarrow \) Hệ số \(a < 0.\)
Đồ thị cắt trục Oy tại điểm có tung độ dương \( \Rightarrow \) Hệ số \(d > 0.\)
Hàm số có hai điểm cực trị âm \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - \frac{{2b}}{{3a}} < 0}\\{{x_1}{x_2} = \frac{c}{{3a}} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b < 0}\\{c < 0}\end{array}} \right.} \right.\).
Vậy chỉ có hệ số \(d > 0.\) Chọn B.
Câu 8:
Cho hàm số \(f(x)\) xác định và liên tục trên \(\mathbb{R}\) thỏa mãn \(2\int f \left( x \right){\rm{d}}x + \frac{{{x^3}}}{3} = \int {{f^2}} \left( x \right){\rm{d}}x + x + C\) với \(C\) là hằng số. Diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),\,\,y = 1,\,\,x = 0,\,\,x = 2\) bằng
 Xem đáp án
Xem đáp án
Lấy đạo hàm hai vế của giả thiết, ta được \(2f\left( x \right) + {x^2} = {f^2}\left( x \right) + 1\)
\( \Leftrightarrow {f^2}\left( x \right) - 2f\left( x \right) + 1 = {x^2} \Leftrightarrow {\left[ {f\left( x \right) - 1} \right]^2} = {x^2} \Leftrightarrow \left| {f\left( x \right) - 1} \right| = \left| x \right|.\)
Diện tích hình phẳng cần tính là .\[S = \int\limits_0^2 {\left| {f\left( x \right) - 1} \right|{\rm{d}}x} = \int\limits_0^2 {\left| x \right|{\rm{d}}x} = 2.\] Chọn B.
Câu 9:
Cho hàm số \(f\left( x \right) = \ln \frac{{2018x}}{{x + 1}}.\) Tính tổng \(S = f'\left( 1 \right) + f'\left( 2 \right) + \ldots + f'\left( {2018} \right)\)?
 Xem đáp án
Xem đáp án
Ta có \(f'(x) = {\left( {\ln \frac{{2018x}}{{x + 1}}} \right)^\prime } = \frac{1}{{\frac{{2018x}}{{x + 1}}}} \cdot {\left( {\frac{{2018x}}{{x + 1}}} \right)^\prime } = \frac{{x + 1}}{{2018x}} \cdot \frac{{2018}}{{{{\left( {x + 1} \right)}^2}}} = \frac{1}{{x\left( {x + 1} \right)}}\).
Vậy \[S = f'\left( 1 \right) + f'\left( 2 \right) + \ldots + f'\left( {2018} \right)\]\( = \frac{1}{{1.2}} + \frac{1}{{2.3}} + .. + \frac{1}{{2018.2019}}\)
\( = \frac{1}{1} - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + .. + \frac{1}{{2018}} - \frac{1}{{2019}}\)\( = 1 - \frac{1}{{2019}} = \frac{{2018}}{{2019}}.\) Chọn D.
Câu 10:
Cho hình nón có bán kính đáy bằng 3 và chiều cao bằng 10. Mặt phẳng \((\alpha )\) vuông góc với trục và cách đỉnh của hình nón một khoảng bằng 4 , chia hình nón thành hai phần. Gọi \({V_1}\) là thể tích của phần chứa đỉnh của hình nón đã cho, \({V_2}\) là thể tích của phần còn lại. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}.\)
 Xem đáp án
Xem đáp án
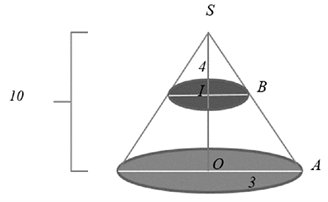
Ta có: \(IB\,{\rm{//}}\,OA \Rightarrow \frac{{IB}}{{OA}} = \frac{{SI}}{{SO}} = \frac{4}{{10}} = \frac{2}{5}\).
Khi đó, \(\frac{{{V_1}}}{V} = \frac{{\frac{1}{3}\pi \cdot I{B^2} \cdot SI}}{{\frac{1}{3}\pi \cdot O{A^2} \cdot SO}}\)
\( = {\left( {\frac{{IB}}{{OA}}} \right)^2} \cdot \left( {\frac{{SI}}{{SO}}} \right) = {\left( {\frac{2}{5}} \right)^3} = \frac{8}{{125}}\).
Suy ra: \(\frac{{{V_2}}}{V} = 1 - \frac{8}{{125}} = \frac{{117}}{{125}}\).
Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{{{V_1}}}{V}:\frac{{{V_2}}}{V} = \frac{8}{{125}}:\frac{{117}}{{125}} = \frac{8}{{117}}\). Chọn CCâu 11:
Các chuyên gia Y tế ước tính số người nhiễm virus Zika kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(f\left( t \right) = 45{t^2} - {t^3},\,\,\left( {t = 0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4 \ldots \,;\,\,25} \right).\) Nếu coi \(f\left( t \right)\) là một hàm xác định trên đoạn \[\left[ {0\,;\,\,25} \right]\] thì \(f'\left( t \right)\) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm \[t.\] Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?
 Xem đáp án
Xem đáp án
Tốc độ truyền bệnh là \(f'\left( t \right) = 90t - 3{t^2} = 675 - 3{\left( {t - 15} \right)^2} \le 675\)
Vậy tốc độ truyền bệnh lớn nhất khi \(t = 15\), tức là vào ngày thứ 15. Chọn C.
Câu 12:
Cho biết phương trình \({\log _3}\left( {{3^{x + 1}} - 1} \right) = 2x + {\log _{\frac{1}{3}}}2\) có hai nghiệm \({x_1},{x_2}.\) Hãy tính tổng \(S = {27^{{x_1}}} + {27^{{x_2}}}?\)
 Xem đáp án
Xem đáp án
Ta có \({\log _3}\left( {{3^{x + 1}} - 1} \right) = 2x + {\log _{\frac{1}{3}}}2 \Leftrightarrow {\log _3}2\left( {{3^{x + 1}} - 1} \right) = 2x\)
\( \Leftrightarrow {2.3^{x + 1}} - 2 = {3^{2x}} \Leftrightarrow {3^{2x}} - {6.3^x} + 2 = 0.\)
Đặt \({3^x} = t\,\,\left( {t > 0} \right)\), phương trình trở thành \({t^2} - 6t + 2 = 0.\)
Phương trình luôn có hai nghiệm dương phân biệt.
Đặt \({3^{{x_1}}} = {t_1},{3^{{x_2}}} = {t_2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{t_1} + {t_2} = 6}\\{{t_1} \cdot {t_2} = 2}\end{array}} \right.\)
Vậy \(S = \left( {t_1^3 + t_2^3} \right) = {\left( {{t_1} + {t_2}} \right)^3} - 3{t_1} \cdot {t_2}\left( {{t_1} + {t_2}} \right) = 216 - 3.2.6 = 180.\) Chọn D.
Câu 13:
Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT X theo từng khối như sau: khối 10 có 5 học sinh, khối 11 có 5 học sinh và khối 12 có 5 học sinh. Nhà trường cần chọn một đội tuyển gồm 10 học sinh tham gia IOE cấp tỉnh. Tính số cách lập đội tuyển sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10.
 Xem đáp án
Xem đáp án
− Nếu trong 10 học sinh được chọn có 1 học sinh lớp 10 và 9 học sinh còn lại trong 10 học sinh khối 11 và 12 thì có số cách lập đội là \(C_5^1 \cdot C_{10}^9 = 50\) (cách).
− Nếu trong 10 học sinh được chọn có 2 học sinh lớp 10 và 8 học sinh còn lại trong 10 học sinh khối 11 và 12 thì có số cách lập đội là \(C_5^2 \cdot C_{10}^8 = 450\) (cách).
Vậy tổng số cách lập đội là \(50 + 450 = 500\) (cách). Chọn B.
Câu 14:
Tìm số các giá trị nguyên của tham số \(m \in \left[ { - 2022\,;\,\,2022} \right]\) sao cho \(\left\{ {\begin{array}{*{20}{l}}{x = - 1}\\{y = 2}\end{array}} \right.\) là nghiệm của bất phương trình \(mx + \left( {m - 1} \right)y > 2\) ?
 Xem đáp án
Xem đáp án
Ta có \(\left\{ {\begin{array}{*{20}{l}}{x = - 1}\\{y = 2}\end{array}} \right.\) là nghiệm của bất phương trình \(mx + (m - 1)y > 2\) nên
\(m + 2(m - 1) > 2 \Leftrightarrow m > 4\).
Mà \(m \in \left[ { - 2022\,;\,\,2022} \right] \Leftrightarrow - 2022 \le m \le 2022\) nên \(4 < m \le 2022\).
Do \(m \in \mathbb{Z}\) nên \(m \in \left\{ {5\,;\,\,6\,;\,\,7\,;\,\, \ldots ;\,\,2022} \right\}\).
Số các giá trị nguyên của tham số \(m\) thỏa mãn đề là \(2022 - 5 + 1 = 2018\) (số). Chọn C.
Câu 15:
Một cửa hàng bán áo sơ mi, quần âu nam và váy nữ. Ngày thứ nhất bán được 12 áo, 21 quần và 18 váy doanh thu là 5349000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5600000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5259000 đồng. Hỏi tổng số tiền mỗi áo, mỗi quần, mỗi váy là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi \[x,\,\,y,\,\,z\] lần lượt là giá tiền một cái áo, một cái quần và một cái váy. Khi đó ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{12x + 21y + 18z = 5\,\,349\,\,000}\\{16x + 24y + 12z = 5\,\,600\,\,000}\\{24x + 15y + 12z = 5\,\,259\,\,000}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 98\,\,000}\\{y = 125\,\,000}\\{z = 86\,\,000}\end{array}} \right.} \right.\)
Suy ra tổng số tiền mỗi áo, mỗi quần, mỗi váy là \(98\,\,000 + 125\,\,000 + 86\,\,000 = 309\,\,000\) (đồng).
Chọn B.
Câu 16:
Số điểm biểu diễn nghiệm của phương trình \(\sin 4x\left( {2\cos x - \sqrt 2 } \right) = 0\) trên đường tròn lượng giác là
 Xem đáp án
Xem đáp án
Ta có
\(\sin 4x\left( {2\cos x - \sqrt 2 } \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin 4x = 0}\\{2\cos x - \sqrt 2 = 0}\end{array}} \right.\)
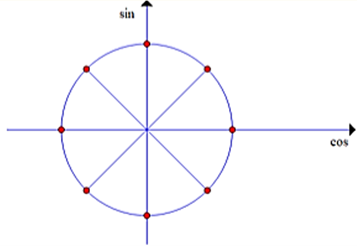
Vậy có 8 điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác. Chọn C.
Câu 17:
Trong không gian với hệ tọa độ \[Oxyz,\] cho hình thang cân \[ABCD\] có các đáy lần lượt là \[AB,\,\,CD.\] Biết \(A\left( {3\,;\,\,1\,;\,\, - 2} \right),\,\,B\left( { - 1\,;\,\,3\,;\,\,2} \right),\,\,C\left( { - 6\,;\,\,3\,;\,\,6} \right)\) và \(D\left( {a\,;\,\,b\,;\,\,c} \right)\) với \(a,\,\,b,\,\,c \in \mathbb{R}.\) Tính \(T = a + b + c.\)
 Xem đáp án
Xem đáp án
Do \[ABCD\] là hình thang cân nên hay \(\frac{{a + 6}}{{ - 2}} = \frac{{b - 3}}{1} = \frac{{c - 6}}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{b = \frac{{ - a}}{2}}\\{c = - a}\end{array}} \right.\).
Vậy \(D\left( {a\,;\,\,\frac{{ - a}}{2}\,;\,\, - a} \right).\)
Lại có \(AC = BD \Leftrightarrow A{C^2} = B{D^2} \Leftrightarrow {\left( { - 9} \right)^2} + {2^2} + {8^2} = {\left( {a + 1} \right)^2} + {\left( {\frac{a}{2} + 3} \right)^2} + {\left( {a + 2} \right)^2}\)
\( \Leftrightarrow {a^2} + 4a - 60 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = 6}\\{a = - 10}\end{array}} \right.\).
Với \(a = - 10 \Rightarrow D\left( { - 10\,;\,\,5\,;\,\,10} \right).\) Kiểm tra thấy: \(\overrightarrow {AB} = \overrightarrow {CD} .\)
Vớí \(a = 6 \Rightarrow D\left( {6\,;\,\, - 3\,;\,\, - 6} \right).\)
Kiểm tra thấy: \(\left( { - 3} \right) \cdot \overrightarrow {AB} = \overrightarrow {CD} .\) Do đó \(T = a + b + c = 6 - 3 - 6 = - 3.\)
Cách 2: Ta có \[\overrightarrow {AB} = \left( { - 4\,;\,\,2\,;\,\,4} \right);\,\,\overrightarrow {CD} = \left( {a + 6\,;\,\,b - 3\,;\,\,c - 6} \right)\]
Do \[ABCD\] là hình thang cân nên \(\overrightarrow {AB} \,;\,\,\overrightarrow {CD} \) ngược hướng hay
\(\frac{{a + 6}}{{ - 2}} = \frac{{b - 3}}{1} = \frac{{c - 6}}{2} < 0\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = \frac{{ - a}}{2}}\\{c = - a}\\{a > - 6}\end{array}} \right.\).
Do đó \(D\left( {a\,;\,\,\frac{{ - a}}{2}\,;\,\, - a} \right)\) với \(a > - 6.\)
Lại có \(AC = BD \Leftrightarrow A{C^2} = B{D^2} \Leftrightarrow {\left( { - 9} \right)^2} + {2^2} + {8^2} = {\left( {a + 1} \right)^2} + {\left( {\frac{a}{2} + 3} \right)^2} + {\left( {a + 2} \right)^2}\)
\( \Leftrightarrow {a^2} + 4a - 60 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = 6}\\{a = - 10\,\,(\;{\rm{L}})}\end{array}} \right.\)
Với \(a = 6 \Rightarrow D\left( {6\,;\,\, - 3\,;\,\, - 6} \right).\)
Do đó, \(T = a + b + c = 6 - 3 - 6 = - 3.\)
Cách 3: Viết phương trình mặt phẳng trung trực của đoạn thẳng \[AB\].
Gọi mặt phẳng \((\alpha )\) là mặt phẳng trung trực của đoạn thẳng \[AB\].
Khi đó, mặt phẳng \((\alpha )\) đi qua trung điểm \(I\left( {1\,;\,\,2\,;\,\,0} \right)\) của đoạn thẳng AB và có một vectơ pháp tuyến \(\overrightarrow n = \frac{1}{2}\overrightarrow {AB} = \left( { - 2\,;\,\,1\,;\,\,2} \right).\)
Suy ra phương trình của mặt phẳng \((\alpha )\) là: \((\alpha ): - 2x + y + 2z = 0.\)
Vì \[C,\,\,D\] đối xứng nhau qua mặt phẳng \((\alpha )\) nên \(D\left( {6\,;\,\, - 3\,;\,\, - 6} \right)\).
Do đó \[a = 6\,;\,\,b = - 3\,;\,\,c = - 6 \Rightarrow T = a + b + c = - 3\]. Chọn A.
Câu 18:
 Xem đáp án
Xem đáp án
Ta có \[f\left( x \right) \cdot f'\left( x \right) - {\left[ {f\left( x \right)} \right]^2} = 2{e^{6x}} \Leftrightarrow 2{e^{ - 2x}}\left[ {f\left( x \right) \cdot f'\left( x \right) - {f^2}\left( x \right)} \right] = 4{e^{4x}}\]
\( \Leftrightarrow \left[ {{e^{ - 2x}} \cdot {f^2}\left( x \right)} \right] = 4{e^{4x}} \Rightarrow {e^{ - 2x}} \cdot {f^2}\left( x \right) = {e^{4x}} + C.\)
• \[f\left( 0 \right) = 1 \Rightarrow {e^0} \cdot {f^2}\left( 0 \right) = {e^0} + C \Rightarrow C = 0.\]
• \(f\left( 1 \right) = a \cdot {e^b} \Rightarrow {e^{ - 2}} \cdot {f^2}\left( 1 \right) = {e^4} \Rightarrow {f^2}\left( 1 \right) = {e^6} \Rightarrow f\left( 1 \right) = {e^3}.\)
Vậy \(a = 1\,,\,\,b = 3 \Rightarrow a + b = 4.\) Chọn A.
Câu 19:
Tính đến đầu năm 2011, dân số toàn tỉnh Bình Phước đạt gần \[905\,\,300,\] mức tăng dân số là \[1,37\% \] mỗi năm. Tỉnh thực hiện tốt chủ trương \[100\% \] trẻ em đúng độ tuổi đều vào lớp 1. Đến năm học 2024 – 2025 ngành giáo dục của tỉnh cần chuẩn bị bao nhiêu phòng học cho học sinh lớp 1, mỗi phòng dành cho 35 học sinh? (Giả sử trong năm sinh của lứa học sinh vào lớp 1 đó toàn tỉnh có \[2\,\,400\] người chết, số trẻ tử vong trước 6 tuổi không đáng kể).
 Xem đáp án
Xem đáp án
Chỉ những em sinh năm 2018 mới đủ tuổi đi học (6 tuổi) vào lớp 1 năm học 2024-2025.
Áp dụng công thức \({S_n} = A{\left( {1 + r\% } \right)^n}\) để tính dân số năm 2018.
Trong đó \(A = 905\,\,300\,;\,\,r = 1,37\% \,;\,\,n = 8.\)
Dân số năm 2018 là \(A = 905\,\,300 \cdot {\left( {1 + 1,37\% } \right)^8} = 1\,\,009\,\,411\) (người).
Dân số năm 2017 là \(A = 905\,\,300 \cdot {\left( {1 + 1,37\% } \right)^7} = 995\,\,769\) (người).
Số trẻ vào lớp 1 là \(100\,\,9411 - 99\,\,5769 + 2\,\,400 = 16\,\,042\) (người).
Số phòng học cần chuẩn bị là \(16\,\,042:35 \approx 459\) (phòng). Chọn C.
Câu 20:
Trong không gian với hệ tọa độ \[Oxyz,\] cho hai điểm \(A\left( {1\,;\,\,2\,;\,\, - 3} \right),B\left( { - 2\,;\,\, - 2\,;\,\,1} \right)\) và mặt phẳng \((\alpha ):2x + 2y - z + 9 = 0\). Gọi \(M\) là điểm thay đổi trên mặt phẳng \((\alpha )\) sao cho \(M\) luôn nhìn đoạn AB dưới một góc vuông. Xác định phương trình đường thẳng \[MB\] khi \[MB\] đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
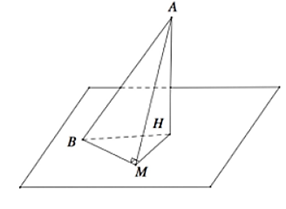
Ta có: \(2 \cdot \left( { - 2} \right) + 2 \cdot \left( { - 2} \right) - 1 + 9 = 0 \Rightarrow B \in (\alpha ).\)
Gọi \(H\) là hình chiếu của \(A\) trên \((\alpha )\) thì \(AH \bot MB,\,\,AM \bot MB\)
\( \Rightarrow MH \bot MB \Rightarrow MB \le BH{\rm{.}}\)
Dấu bằng xảy ra khi \(M \equiv H\), lúc đó \(M\) là hình chiếu của \(A\) trên \((\alpha ).\)
Gọi \(H\left( {x\,;\,\,y\,;\,\,z} \right),\,\,\overrightarrow {AH} = \left( {x - 1\,;\,\,y - 2\,;\,\,z + 3} \right)\). Chọn C.Câu 21:
 Xem đáp án
Xem đáp án
Ta có \(\left\{ {\begin{array}{*{20}{l}}{{x^2} + {y^2} - xy + x + y = 8}\\{xy + 3\left( {x + y} \right) = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{\left( {x + y} \right)}^2} - 3xy + x + y = 8}\\{xy + 3\left( {x + y} \right) = 1}\end{array}} \right.} \right.\)
Đặt \(\left\{ {\begin{array}{*{20}{l}}{x + y = S}\\{xy = P}\end{array}\,;\,\,{S^2} \ge 4P} \right.\), hệ đã cho trở thành \(\left\{ {\begin{array}{*{20}{l}}{{S^2} + S - 3P = 8}\\{3S + P = 1}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{S^2} + S - 3\left( {1 - 3S} \right) = 8}\\{P = 1 - 3S}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{S^2} + 10S - 11 = 0}\\{P = 1 - 3S}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{S = 1}\\{P = - 2}\end{array}\,\,(\;{\rm{N}})} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{S = - 11}\\{P = 34}\end{array}\,\,(\;{\rm{L}})} \right.}\end{array}} \right.} \right.} \right.\)
Với \(S = 1\,;\,\,P = - 2\) ta có \[x;{\rm{ }}y\] là nghiệm của phương trình \({t^2} + t - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 1}\\{t = - 2}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {1\,;\,\, - 2} \right);\,\,\left( { - 2\,;\,\,1} \right) \Rightarrow \left| {{x_1} - {x_2}} \right| = \left| {1 - \left( { - 2} \right)} \right| = \left| { - 2 - 1} \right| = 3.\)
Chọn A.
Câu 22:
Cho hàm số \(f\left( x \right) = {x^3} - 6{x^2} + 9x + 2.\) Tìm tất cả các giá trị của tham số \(m\) sao cho bất phương trình \(f\left( {3x + 1} \right) + 9{x^2} - 6x + 1 \le m\) đúng với mọi \[x \in \left[ {0\,;\,1} \right]\]?
 Xem đáp án
Xem đáp án
Ta có \(f'\left( x \right) = 3{x^2} - 12x + 9.\)
Xét hàm số \[g\left( x \right) = f\left( {3x + 1} \right) + 9{x^2} - 6x + 1\] ta có \(g'\left( x \right) = 3f'\left( {3x + 1} \right) + 18x - 6\).
Suy ra \(g'\left( x \right) = 0 \Leftrightarrow f'\left( {3x + 1} \right) = - 2\left( {3x + 1} \right) + 4.\) (1)
Đặt \(t = 3x + 1\) khi đó mọi \(x \in \left[ {0\,;\,\,1} \right] \Rightarrow t \in \left[ {1\,;\,\,4} \right]\), khi đó (1) trở thành
\(f'\left( t \right) = - 2t + 4 \Leftrightarrow 3{t^2} - 10t + 5 = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = \frac{{5 - \sqrt {10} }}{3} \notin \left[ {1\,;\,\,4} \right]}\\{t = \frac{{5 + \sqrt {10} }}{3} \in \left[ {1\,;\,\,4} \right]}\end{array}} \right.\).
Ta có \(g\left( 1 \right) = 3\,;\,\,g\left( 4 \right) = 10\,;\,\,g\left( {\frac{{3 + \sqrt {10} }}{3}} \right) \approx 0,3 \Rightarrow {\max _{\left[ {1\,;\,\,4} \right]}}g(t) = 10.\)
Do đó để \(f\left( {3x + 1} \right) + 9{x^2} - 6x + 1 \le m \Rightarrow m \ge 10.\) Chọn C.
Câu 23:
Trong hệ tọa độ Oxy cho Gọi \(C\left( {a;\,b} \right)\) thuộc đường thẳng \(d:x - 2y - 1 = 0\) sao cho khoảng cách từ \(C\) đến đường thẳng \[AB\] bằng 6 . Biết rằng \(C\) có hoành độ nguyên. Tính \(a + b\).
 Xem đáp án
Xem đáp án
Ta có \(\overrightarrow {AB} = (3; - 4).\)
Khi đó, phương trình của đường thẳng \[AB\] có dạng: \(4x + 3y + m = 0.\)
Vì \(A\left( {1\,;\,\,1} \right) \in AB\) nên \[4 \cdot 1 + 3 \cdot 1 + m = 0 \Leftrightarrow m = - 7 \Rightarrow AB:4x + 3y - 7 = 0.\]
Vi \(C\left( {a\,;\,\,b} \right) \in d:x - 2y - 1 = 0 \Rightarrow a - 2b - 1 = 0 \Rightarrow a = 2b + 1.\)
Theo đề ra \[{\rm{d}}\left( {C\,,\,\,AB} \right) = 6 \Leftrightarrow \frac{{\left| {4a + 3b - 7} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 6 \Leftrightarrow \left| {4a + 3b - 7} \right| = 30.\]
Thay \(a = 2b + 1\) vào ta được: \(\left| {4\left( {2b + 1} \right) + 3b - 7} \right| = 30\)
\( \Leftrightarrow \left| {11b - 3} \right| = 30 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{11b - 3 = 30}\\{11b - 3 = - 30}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{b = 3}\\{b = - \frac{{27}}{{11}}}\end{array}} \right.} \right.\).
Do \(C\) có tọa độ nguyên nên \(b = 3\,;\,\,a = 7 \Rightarrow a + b = 10.\) Chọn A.
Câu 24:
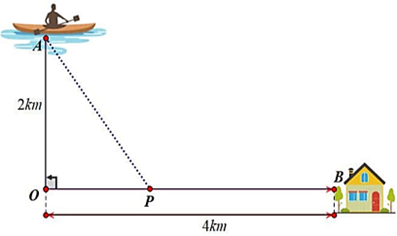
Bạn Hưng đang trên chiếc thuyền tại vị trí \[A\] cách bờ sông \(2\;\,{\rm{km}}\), bạn dự định chèo thuyền vào bờ và tiếp tục chạy bộ theo một đường thẳng để đến một địa điểm \({\rm{B}}\) tọa lạc ven bờ sông, \({\rm{B}}\) cách vị trí \[O\] trên bờ gần với thuyền nhất là \(4\;\,{\rm{km}}\) (hình vẽ). Biết rằng bạn Hưng chèo thuyền với vậntốc \(6\;\,{\rm{m}}/{\rm{h}}\) và chạy bộ trên bờ với vận tốc \(10\;\,{\rm{km}}/{\rm{h}}.\) Khoảng thời gian ngắn nhất để bạn Hưng từ vị trí xuất phát đến được điểm B là\[A\left( {1\,;\,\,1} \right),\,\,B\left( {4\,;\,\, - 3} \right).\]
 Xem đáp án
Xem đáp án
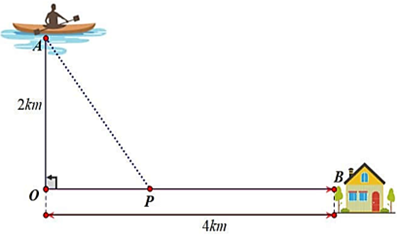
Đặt \(OP = x\,\,(0 < x < 4) \Rightarrow BP = 4 - x\,;\,\,AP = \sqrt {4 + {x^2}} .\)
Khoảng thời gian để anh Ba từ vị trí xuất phát đến được điểm \(B\) là:
\({t_{\left( x \right)}} = {t_{AP}} + {t_{PB}} = \frac{{\sqrt {4 + {x^2}} }}{6} + \frac{{4 - x}}{{10}}(h)\,\, \Rightarrow {t'_{\left( x \right)}} = \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}}.\)
\({t'_{\left( x \right)}} = 0 \Leftrightarrow \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}} = 0 \Leftrightarrow 3\sqrt {4 + {x^2}} = 5x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 < x < 4}\\{4{x^2} = 9}\end{array} \Leftrightarrow x = \frac{3}{2}.} \right.\)
Bảng biến thiên:
|
\(x\) |
0 |
\(\frac{3}{2}\) |
4 |
|
\(t'\left( x \right)\) |
\( - \) |
0 + |
|
|
\(t\left( x \right)\) |
\(\frac{{11}}{{15}}\)
|
|
\(\frac{{\sqrt 5 }}{3}\)
|
|
|
|
\(\frac{2}{3}\) |
|
Từ bảng biến thiên suy ra khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm \({\rm{B}}\) là: \({t_{\min }} = \frac{2}{3}(h) = \frac{2}{3}.60\) (phút) \( = 40\) (phút). Chọn A.
Câu 25:
 Xem đáp án
Xem đáp án
Cách 1:
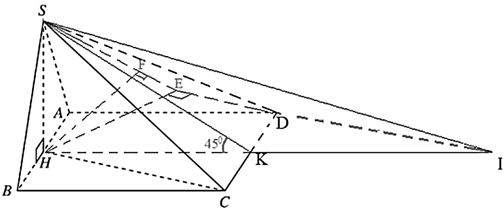
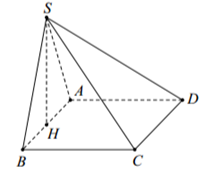
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SAB} \right) \bot \left( {ABCD} \right)}\\{\left( {SAB} \right) \cap \left( {ABCD} \right)}\\{SH \bot AB\,;\,\,SH \subset \left( {SAB} \right)}\end{array} \Rightarrow SH \bot \left( {ABCD} \right)} \right..\)
Kẻ \(HK \bot CD\,\,\left( {K \in CD} \right)\).
Ta có \(\left\{ \begin{array}{l}CD \bot HK\\CD \bot SH\end{array} \right.\)\( \Rightarrow CD \bot (SHK) \Rightarrow CD \bot SK.\)
Gọi \(I\) là điểm đối xứng \(H\) qua \(K.\)
Dễ dàng chứng minh \(\Delta CKH = \Delta DKI\,\,(c.g.c)\) suy ra \(\widehat {CKH} = \widehat {DKI}\) (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên \[DI\,{\rm{//}}\,HC\] suy ra \[HC\,{\rm{//}}\,\left( {SDI} \right)\]
\[ \Rightarrow d\left( {HC;\,\,SD} \right) = d\left( {HC;\,\,\left( {SID} \right)} \right) = d\left( {H;\,\,\left( {SID} \right)} \right).\]
Trong \(\left( {ABCD} \right)\), kẻ \(HE \bot DI\,\,\left( {E \in DI} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HF \bot SE\,\,\left( {F \in SE} \right).\)
Ta có \(\left\{ \begin{array}{l}DI \bot HE\\DI \bot SH\end{array} \right. \Rightarrow DI \bot \left( {SHE} \right) \Rightarrow DI \bot HF.\)
\[\left\{ \begin{array}{l}HF \bot SE\\HF \bot DI\end{array} \right. \Rightarrow HF \bot \left( {SCD} \right)\]
\[ \Rightarrow d\left( {H;\,\,\left( {SID} \right)} \right) = HF = d\left( {HC;\,\,SD} \right)\].
+) Tính \(HE\):
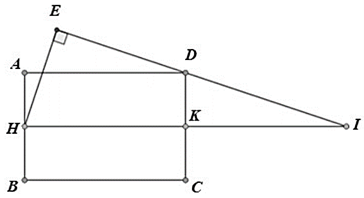
• Xét \(\Delta DKI\) vuông tại \(K\) có \(\sin I = \frac{{DK}}{{DI}} = \frac{a}{{\sqrt {{a^2} + {{\left( {3a} \right)}^2}} }} = \frac{1}{{\sqrt {10} }}.\)
• Xét \(\Delta HIE\) vuông tại \(E\) có \[HE = HI \cdot \sin I = 6a \cdot \frac{1}{{\sqrt {10} }} = \frac{{3a\sqrt {10} }}{5}.\]
+) Tính \(SH\):
Khi đó ta có \[\left\{ {\begin{array}{*{20}{l}}{\left( {SCD} \right) \bot \left( {ABCD} \right) = CD}\\{HK \subset \left( {ABCD} \right),\,\,HK \bot CD}\\{SK \bot \left( {SCD} \right)\,;\,\,SK \bot CD}\end{array}} \right.\]
\[ \Rightarrow \widehat {\left( {\left( {SCD} \right);\,\,\left( {ABCD} \right)} \right)} = \widehat {\left( {SK;\,\,HK} \right)} = \widehat {SKH} = 45^\circ \].
Suy ra \(\Delta SKH\) vuông cân tại \(H \Rightarrow SH = HK = AD = 3a.\)
+) Tính \(HF\):
Xét tam giác \[SHE\] vuông tại \(H\) có \(HF\) là đường cao nên
\(\frac{1}{{H{F^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{E^2}}} = \frac{1}{{9{a^2}}} + \frac{1}{{\frac{{18}}{5}{a^2}}} = \frac{7}{{18{a^2}}} \Rightarrow HF = \frac{{3a\sqrt {14} }}{7}.\)
Vậy \[{\rm{d}}\left( {SD\,;\,\,CH} \right) = \frac{{3\sqrt {14} a}}{7}{\rm{.}}\] Chọn B.
Câu 26:
 Xem đáp án
Xem đáp án
Ta có \(f\left( x \right) = 6f\left( {3x - 1} \right) \Leftrightarrow \int\limits_2^3 {f\left( x \right){\rm{d}}x} = \int\limits_2^3 {6f\left( {3x - 1} \right){\rm{d}}x} \)
\( \Leftrightarrow \int\limits_2^3 {f\left( x \right){\rm{d}}x} = \int\limits_2^3 {6f\left( {3x - 1} \right){\rm{d}}x} = 2 \cdot \int\limits_2^3 {f\left( {3x - 1} \right){\rm{d}}\left( {3x - 1} \right)} = 2 \cdot \int\limits_5^8 {f\left( x \right){\rm{d}}x} \).
Suy ra \[\int\limits_5^8 {f\left( x \right){\rm{d}}x} = \frac{1}{2} \cdot \int\limits_2^3 {f\left( x \right){\rm{d}}x} = \frac{1}{2} \cdot \left[ {F\left( 3 \right) - F\left( 2 \right)} \right] = \frac{1}{2} \cdot \left( { - 24} \right) = - 12.\]
Chọn A.
Câu 27:
 Xem đáp án
Xem đáp án
Ta có \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) suy ra \(y' = 4a{x^3} + 2bx\)
Hàm số đạt cực trị tại \(x = 2 \Rightarrow y'\left( 2 \right) = 0 \Leftrightarrow 0 = 32a + 4b.\)
Đồ thị hàm số đi qua điểm
• \(A\left( {0\,;\,\,2} \right)\) nên \(c = 2\).
• \(B\left( {2\,;\,\, - 14} \right)\) nên \( - 14 = 16a + 4b + 2\).
Từ đó suy ra \(\left\{ \begin{array}{l}a = 1\\b = - 8\\c = 2\end{array} \right. \Rightarrow y = {x^4} - 8{x^2} + 2.\) Vậy \(f\left( 1 \right) = 1 - 8 + 2 = - 5.\) Chọn D.
Câu 28:
Trong mặt phẳng tọa độ \[Oxy,\] gọi \(\left( H \right)\) là tập hợp các điểm biểu diễn hình học của số phức \(z\) thỏa mãn
 Xem đáp án
Xem đáp án
Gọi \[z = x + yi\,\, \Rightarrow \bar z = x - yi.\]
Ta có \[\left\{ {\begin{array}{*{20}{l}}{\left| {z + \bar z} \right| \ge 12}\\{\left| {z - 4 - 3i} \right| \le 2\sqrt 2 }\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2\left| x \right| \ge 12}\\{{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2} \le 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left| x \right| \ge 6}\\{{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2} \le 8}\end{array}\,\,\left( H \right)} \right.} \right.} \right..\]
Diện tích \(\left( H \right)\) là phần tô đậm trong hình vẽ.
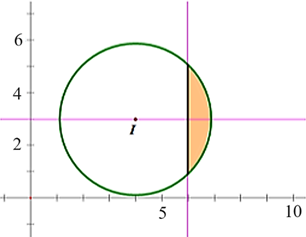
Giải hệ: \(\left\{ {\begin{array}{*{20}{l}}{y = 3}\\{{{\left( {x - 4} \right)}^2} + {{\left( {y - 3} \right)}^2} = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 3}\\{x = 4 \pm 2\sqrt 2 }\end{array}} \right.} \right..\)
Suy ra đồ thị hàm số \(y = 3\) cắt đường tròn \((C)\) tại \(E\left( {4 - 2\sqrt 2 \,;\,\,3} \right)\) và \(F\left( {4 + 2\sqrt 2 \,;\,\,3} \right)\).
Vậy diện tích của hình phẳng \((H)\) là: \(2\int\limits_6^{4 + 2\sqrt 2 } {\left( {3 + \sqrt {8 - {{(x - 4)}^2}} - 3} \right)dx} = 2\pi - 4.\) Chọn C.
Câu 29:
 Xem đáp án
Xem đáp án
Hình hộp có đáy là hình vuông cạnh \[12 - 2x\].
Chiều cao của hình hộp là \[x\].
Thể tích hình hộp là \[y = x{\left( {12 - 2x} \right)^2}\].
Bài toán đưa về tìm \[x \in \left( {0\,;\,\,6} \right)\] để hàm số \[y = f\left( x \right) = x{\left( {12 - 2x} \right)^2}\] có giá trị lớn nhất.
\[y' = 1 \cdot {\left( {12 - 2x} \right)^2} + x \cdot 2 \cdot \left( {12 - 2x} \right) \cdot \left( { - 2} \right) = 12{x^2} - 96x + 144\].
\[y'\] xác định \[\forall x \in \left( {0\,;\,\,6} \right)\]; \[y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 6\end{array} \right..\]
Bảng biến thiên
|
\(x\) |
0 |
2 |
6 |
|
\(y'\) |
+ |
0 \( - \) |
|
|
\(y\) |
|
128 |
|
|
|
0 |
|
0 |
Hàm số đạt giá trị lớn nhất tại \[x = 2\]. Chọn A.
Câu 30:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
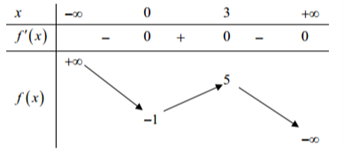
Có bao nhiêu số nguyên \(m\) để hàm số \(g\left( x \right) = 2{f^2}\left( x \right) \cdot \left[ {f\left( x \right) - 3m} \right]\) có 4 điểm cực tiểu?
 Xem đáp án
Xem đáp án
Ta có \[g\left( x \right) = 2{f^3}\left( x \right) - 6m \cdot {f^2}\left( x \right)\]
\( \Rightarrow g'\left( x \right) = 6f'\left( x \right) \cdot {f^2}\left( x \right) - 12m \cdot f'\left( x \right) \cdot f\left( x \right)\)\( = 6f'\left( x \right) \cdot f\left( x \right) \cdot [f\left( x \right) - 2m] = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f'\left( x \right) = 0}\\{f\left( x \right) = 0}\\{f\left( x \right) = 2m}\end{array}} \right.\)
Dễ thấy \(f'\left( x \right) = 0\) có hai nghiệm là \(x = 0\,;\,\,x = 3\)
Và \(f\left( x \right) = 0\) có ba nghiệm thực phân biệt.
Yêu cầu bài toán \[ \Leftrightarrow g'(x) = 0\] có 8 nghiệm đơn phân biệt
\( \Leftrightarrow (*)\) có ba nghiệm đơn phân biệt \( \Leftrightarrow - 1 < 2m < 5 \Leftrightarrow - \frac{1}{2} < m < \frac{5}{2}.\)
Mà \(m \in \mathbb{Z}\) suy ra \(m \in \left\{ {0\,;\,\,1\,;\,\,2} \right\}.\) Chọn A.
Câu 31:
Trong không gian \[Oxy,\] cho điểm \(I\left( {1\,;\,\, - 2\,;\,\,3} \right).\) Viết phương trình mặt cầu tâm \(I\), cắt trục \[Ox\] tại hai điểm \(A\) và \(B\) sao cho \(AB = 2\sqrt 3 .\)
 Xem đáp án
Xem đáp án
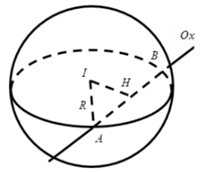
Gọi \[H\] là trung điểm \[AB\].
Suy ra \[H\] là hình chiếu vuông góc của \[I\] lên Ox nên \[H\left( {1\,;\,\,0\,;\,\,0} \right).\]
Khi đó \(IH = \sqrt {13} \Rightarrow R = IA = \sqrt {I{H^2} + A{H^2}} = 4.\)
Phương trình mặt cầu là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 16.\)
Chọn A.
Câu 32:
Cho \(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - 10}}{{x - 1}} = 5\) và \(g\left( x \right) = \sqrt {f\left( x \right) + 6} - 2\sqrt[3]{{f\left( x \right) - 2}}.\) Tính \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{\left( {\sqrt x - 1} \right)g\left( x \right)}}\).
 Xem đáp án
Xem đáp án
\(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - 10}}{{x - 1}} = 5{\rm{ n\^e n }}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - 10} \right] = 0 \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = 10\)
Ta có \(g\left( x \right) = \sqrt {f\left( x \right) + 6} - 2\sqrt[3]{{f\left( x \right) - 2}} = \left[ {\sqrt {f\left( x \right) + 6} - 4} \right] - \left[ {2\sqrt[3]{{f\left( x \right) - 2}} - 4} \right]\)
\( = \frac{{f\left( x \right) - 10}}{{\sqrt {f\left( x \right) + 6} + 4}} - \frac{{2\left[ {f\left( x \right) - 10} \right]}}{{{{\left[ {\sqrt[3]{{f\left( x \right) - 2}}} \right]}^2} + 2\sqrt[3]{{f\left( x \right) - 2}} + 4}}\)
Suy ra \(\left( {\sqrt x - 1} \right)g\left( x \right) = \left[ {\frac{{f\left( x \right) - 10}}{{\sqrt {f\left( x \right) + 6} + 4}} - \frac{{2\left( {f\left( x \right) - 10} \right)}}{{{{\left( {\sqrt[3]{{f\left( x \right) - 2}}} \right)}^2} + 2\sqrt[3]{{f\left( x \right) - 2}} + 4}}} \right]\left( {\sqrt x - 1} \right)\)
\[ = \frac{{f\left( x \right) - 10}}{{x - 1}}\left[ {\frac{1}{{\sqrt {f\left( x \right) + 6} + 4}} - \frac{2}{{{{\left( {\sqrt[3]{{f\left( x \right) - 2}}} \right)}^2} + 2\sqrt[3]{{f\left( x \right) - 2}} + 4}}} \right]\left( {x - 1} \right)\left( {\sqrt x - 1} \right)\]
\( = \frac{{f\left( x \right) - 10}}{{x - 1}}\left[ {\frac{1}{{\sqrt {f\left( x \right) + 6} + 4}} - \frac{2}{{{{\left( {\sqrt[3]{{f\left( x \right) - 2}}} \right)}^2} + 2\sqrt[3]{{f\left( x \right) - 2}} + 4}}} \right]\left( {\sqrt x + 1} \right){\left( {\sqrt x - 1} \right)^2}\)
Khi đó \(\mathop {\lim }\limits_{x \to 1} \left( {\sqrt x - 1} \right)g\left( x \right)\)
\( = \mathop {\lim }\limits_{x \to 1} \left[ {\frac{{f\left( x \right) - 10}}{{x - 1}}\left( {\frac{1}{{\sqrt {f\left( x \right) + 6} + 4}} - \frac{2}{{{{\left( {\sqrt[3]{{f\left( x \right) - 2}}} \right)}^2} + 2\sqrt[3]{{f\left( x \right) - 2}} + 4}}} \right)\left( {\sqrt x + 1} \right){{\left( {\sqrt x - 1} \right)}^2}} \right]\)
\( = 5\left[ {\frac{1}{{\sqrt {10 + 6} + 4}} - \frac{2}{{{{\left( {\sqrt[3]{{10 - 2}}} \right)}^2} + 2\sqrt[3]{{10 - 2}} + 4}}} \right]\left( {\sqrt 1 + 1} \right){\left( {\sqrt 1 - 1} \right)^2} = 0\)
Mặt khác \(\mathop {\lim }\limits_{x \to 1} \left[ {\frac{{f\left( x \right) - 10}}{{x - 1}}\left( {\frac{1}{{\sqrt {f\left( x \right) + 6} + 4}} - \frac{2}{{{{\left( {\sqrt[3]{{f\left( x \right) - 2}}} \right)}^2} + 2\sqrt[3]{{f\left( x \right) - 2}} + 4}}} \right)\left( {\sqrt x + 1} \right)} \right] = - \frac{5}{{12}}{\rm{. }}\)
Và \({\left( {\sqrt x - 1} \right)^2} > 0\) với \(\forall x \ne 1\) nên \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{\left( {\sqrt x - 1} \right)g\left( x \right)}} = - \infty \). Chọn A.
Câu 33:
Cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) thỏa mãn \(\left| {z - 3 + i} \right| - \left| {z + 2 + 2i} \right| = \sqrt {26} \). Biểu thức \(T = \left| {4 - \left( {3 + z} \right)i} \right|\) đạt giá trị nhỏ nhất khi \(b - a\) bằng
 Xem đáp án
Xem đáp án
Gọi \(M\left( {a\,;\,\,b} \right),A\left( {3\,;\,\, - 1} \right),B\left( { - 2\,;\,\, - 2} \right)\) là các điểm biểu diễn các số phức \(z\,;\,\,3 - i\,;\,\, - 2 - 2i.\)
Khi đó \(\left| {z - 3 + i} \right| - \left| {z + 2 + 2i} \right| = \sqrt {26} \Leftrightarrow MA - MB = \sqrt {26} = AB\).
Suy ra \[M\] nằm trên đường thẳng \[AB\], về nằm về phía điểm \[B\].
Ta có \(T = \left| {4 - \left( {3 + z} \right)i} \right| = \left| {4 - 3i - iz} \right| = \left| i \right|.\left| {\frac{{4 - 3i}}{i} - z} \right| = \left| {z + 3 + 4i} \right| = MC\)
Với \(C\left( { - 3\,;\,\, - 4} \right)\) biểu diễn số phức \( - 3 - 4i.\)
Do đó \({T_{\min }} \Leftrightarrow MC\) ngắn nhất \( \Leftrightarrow M\) là hình chiếu của \(C\) trên \[AB\].
Phương trình đường thẳng \[AB\] là \(\left( {{d_1}} \right):x - 5y - 8 = 0.\)
Phương trình đường thẳng qua \(C\), vuông góc với \[AB\] là \(\left( {{d_2}} \right):5x + y + 19 = 0.\)
Suy ra \[M\] là giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right) \Rightarrow M\left( { - \frac{{87}}{{26}}; - \frac{{59}}{{26}}} \right) \Rightarrow b - a = \frac{{14}}{{13}}.\) Chọn A.
Câu 34:
 Xem đáp án
Xem đáp án
Ta có \(f'\left( x \right) = - 3{x^2} + 13x - 12 - {e^x} < 0,\,\,\forall x.\)
Do đó \(f\left[ {{{\log }_{0,5}}\left( {{{\log }_2}\left( {2m + 1} \right)} \right) - 2021} \right] < f\left[ {f\left( 0 \right)} \right]\)
\( \Leftrightarrow {\log _{0,5}}\left( {{{\log }_2}(2m + 1)} \right) - 2021 > f\left( 0 \right) = - 2023\)
\( \Leftrightarrow {\log _{0,5}}\left( {{{\log }_2}(2m + 1)} \right) > - 2\)
\( \Leftrightarrow 0 < {\log _2}(2m + 1) < {(0,5)^{ - 2}} = 4 \Leftrightarrow 1 < 2m + 1 < 16\)
\( \Leftrightarrow 0 < m < \frac{{15}}{2} \Rightarrow m \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6\,;\,\,7} \right\}.\) Chọn D.
Câu 35:
Cho hình lập phương \(ABCD \cdot A'B'C'D'\) có độ dài cạnh bằng 1. Gọi \[M,\,\,N,\,\,P,\,\,Q\] lần lượt là trung điểm của \(AB,\,\,BC,\,\,C'D',\,\,DD'.\) Gọi thể tích khối tứ diện \[MNPQ\] là phân số tối giản \(\frac{a}{b}\), với \(a,\,\,b \in {\mathbb{N}^*}.\) Tính \(a + b.\)
 Xem đáp án
Xem đáp án
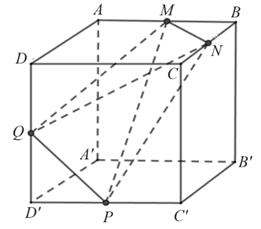
Thiết lập hệ tọa độ \[Oxyz\] như hình vẽ, gốc \(O \equiv A'\,;\,Ox \equiv A'B'\,\,;\,Oy \equiv AA'\,;\,Oz \equiv A'D'.\)
Khi đó \(A'\left( {0\,;\,\,0\,;\,\,0} \right),\,\,A\left( {0\,;\,\,1\,;\,\,0} \right),\,\,B'\left( {1\,;\,\,0\,;\,\,0} \right),D'\left( {0\,;\,\,0\,;\,\,1} \right).\)
Vì \[M,\,\,N,\,\,P,\,\,Q\] lần lượt là trung điểm của \(AB,\,\,BC,\,\,C'D',\,\,DD'\) nên
\(M\left( {1\,;\,\,\frac{1}{2}\,;\,\,0} \right),\,\,N\left( {1\,;\,\,1\,;\,\,\frac{1}{2}} \right),\,\,Q\left( {0\,;\,\,\frac{1}{2}\,;\,\,1} \right),\,\,P\left( {\frac{1}{2}\,;\,\,0\,;\,\,1} \right).\)Ta có \[\overrightarrow {MN} = \left( {\frac{1}{2}\,;\,\,0\,\,;\,\,\frac{1}{2}} \right),\,\,\overrightarrow {MP} = \left( { - \frac{1}{2}\,\,;\,\, - \frac{1}{2}\,\,;\,\,1} \right),\,\,\overrightarrow {MQ} = \left( {0\,\,;\,\, - 1\,\,;\,\,1} \right).\]
\[ \Rightarrow \left[ {\overrightarrow {MN} \,,\,\,\overrightarrow {MP} } \right] = \left( {\frac{1}{4}\,;\,\, - \frac{3}{4}\,;\,\, - \frac{1}{4}} \right) \Rightarrow \left[ {\overrightarrow {MN} \,,\,\,\overrightarrow {MP} } \right] \cdot \overrightarrow {MQ} = \frac{1}{2}\].
Suy ra \({V_{MNPQ}} = \frac{1}{6}\left| {\left[ {\overrightarrow {MN} \,,\,\,\overrightarrow {MP} } \right] \cdot \overrightarrow {MQ} } \right| = \frac{1}{{12}} \Rightarrow a = 1\,;\,\,b = 12 \Rightarrow a + b = 13.\) Chọn C.
Câu 36:
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm là:
\({x^3} - 8{x^2} + 8x = {x^2} + \left( {8 - a} \right)x - b \Leftrightarrow {x^3} - 9{x^2} + ax + b = 0\,\,\,(1)\)
Khi đó phương trình (1) có ba nghiệm nằm trong \(\left[ { - 1\,;\,\,5} \right]\).
Đặt \(f(x) = {x^3} - 9{x^2} + ax + b\) suy ra \(f'\left( x \right) = 3{x^2} - 18x + a.\)
Để phương trình (1) có ba nghiệm nằm trong \(\left[ { - 1\,;\,\,5} \right]\) thì \(f'\left( x \right) = 3{x^2} - 18x + a = 0\) có hai nghiệm phân biệt thuộc \(\left[ { - 1\,;\,\,5} \right]\)\( \Leftrightarrow a = - 3{x^2} + 18x\) có hai nghiệm phân biệt thuộc \(\left[ { - 1\,;\,\,5} \right]\).
Xét hàm số \(g\left( x \right) = - 3{x^2} + 18x\) suy ra \(g'\left( x \right) = - 6x + 18\), ta có \(g'\left( x \right) = 0 \Leftrightarrow x = 3.\)
Bảng biến thiên của \(y = g\left( x \right)\).
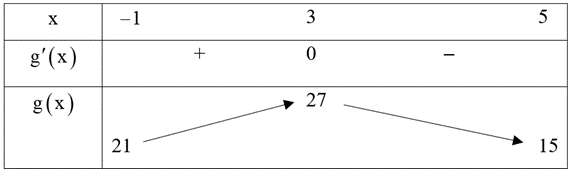
Từ BBT, ta có \(15 \le a < 27\) suy ra giá trị nhỏ nhất của \(a\) bằng 15 khi \(x = 5\), khi đó \(b = 25.\)
Vậy tích \(ab = 375.\)
Đáp án: 375.
Câu 37:
 Xem đáp án
Xem đáp án
Chọn 4 người trong \(n\) học sinh có \(C_n^4\) cách \( \Rightarrow n(\Omega ) = C_n^4.\)
Gọi A là biến cố "trong đội tuyển chính thức có cả hai học sinh nữ"
Và B là biến cố "trong đội tuyển chinh thức không có học sinh nữ nào"
Khi đó \({P_A} = \frac{{C_2^2 \cdot C_{n - 2}^2}}{{C_n^4}}\) và \({P_B} = \frac{{C_{n - 2}^4}}{{C_n^4}}\) suy ra \(\frac{{C_2^2 \cdot C_{n - 2}^2}}{{C_n^4}} = 2 \cdot \frac{{C_{n - 2}^4}}{{C_n^4}} \Rightarrow n = 7.\)
Đáp án: 7.
Câu 38:
 Xem đáp án
Xem đáp án
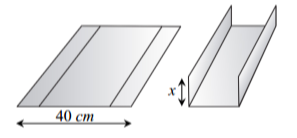
Khi chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông như hình vẽ thì mặt cắt ngang là hình chữ nhật có hai kích thước \(x(\;{\rm{cm}})\) và \(40 - 2x(\;{\rm{cm}}).\)
Khi đó diện tích mặt cắt ngang là \(\left( {40 - 2x} \right)x\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right).\)
Ta thấy: Diện tích mặt cắt ngang của rãnh dẫn nước lớn hơn hoặc bằng \(150\;\,\,{\rm{c}}{{\rm{m}}^2}\) khi và chỉ khi
\(\left( {40 - 2x} \right)x \ge 150 \Leftrightarrow - 2{x^2} + 40x - 150 \ge 0.{\rm{ }}\)
Tam thức \(f(x) = - 2{x^2} + 40x - 150\) có hai nghiệm \({x_1} = 5,{x_2} = 15\) và hệ số \(a = - 2 < 0.\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \(f\left( x \right)\) mang dấu "+" là khoảng \(\left( {5\,;\,\,15} \right).\)
Do đó tập nghiệm của bất phương trình \( - 2{x^2} + 40x - 150 \ge 0\) là đoạn \[\left[ {5\,;\,\,15} \right].\]
Vậy rãnh dẫn nước phải có độ cao ít nhất là \(5\,\;{\rm{cm}}.\)
Đáp án: 5.
Câu 39:
 Xem đáp án
Xem đáp án
Ta có \(y' = f'\left( x \right) = \frac{{ - 4}}{{{{(x + 1)}^2}}}.\)
Phương trình tiếp tuyến của \((C)\) tại điểm \(M\left( {{x_0};{y_0}} \right) \in (C)\) có dạng \[y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.\]
Đường thẳng \(\Delta :y = - 4x + m\) là tiếp tuyến của \((C)\) suy ra \(f'\left( {{x_0}} \right) = - 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{x_0} = - 2}\end{array}} \right..\)
• Với \({x_0} = 0\) ta có phương trình tiếp tuyến là \(y = - 4\left( {x - 0} \right) + 3 \Leftrightarrow y = - 4x + 3.\)
• Với \({x_0} = - 2\),ta có phương trình tiếp tuyến là \(y = - 4\left( {x + 2} \right) - 5 \Leftrightarrow y = - 4x - 13.\)
Vậy có hai giá trị \(m\) thỏa mãn \(\Delta \) là tiếp tuyến của \((C)\) là \(m = 3;m = - 13.\)
Suy ra tổng các giá trị \(m\) là \[ - 10\].
Đáp án: −10.
Câu 40:
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để phương trình \({16^x} - 2 \cdot {12^x} + \left( {m - 2} \right){9^x} = 0\) có nghiệm dương?
 Xem đáp án
Xem đáp án
Ta có \({16^x} - 2 \cdot {12^x} + \left( {m - 2} \right) \cdot {9^x} = 0 \Leftrightarrow {\left( {\frac{{16}}{9}} \right)^x} - 2 \cdot {\left( {\frac{{12}}{9}} \right)^x} + m - 2 = 0\)
\( \Leftrightarrow 2 - m = {\left[ {{{\left( {\frac{4}{3}} \right)}^x}} \right]^2} - 2 \cdot {\left( {\frac{4}{3}} \right)^x}\), đặt \(t = {\left( {\frac{4}{3}} \right)^x} > 1\) nên \(2 - m = {t^2} - 2t = f\left( t \right).\)
\( \Rightarrow f'\left( t \right) = 2t - 2 > 0,\,\,\forall t > 1\) suy ra \(f\left( t \right)\) là hàm số đồng biến trên \(\left( {1\,;\,\, + \infty } \right).\)
Để phương trình \[2 - m = f\left( t \right)\] có nghiệm \( \Leftrightarrow 2 - m > f(1) = - 1 \Leftrightarrow m < 3.\)
Kết hợp với \(m \in {\mathbb{Z}^ + }\)suy ra \(m \in \left\{ {1\,;\,\,2} \right\}.\)
Đáp án: 2.
Câu 41:
 Xem đáp án
Xem đáp án
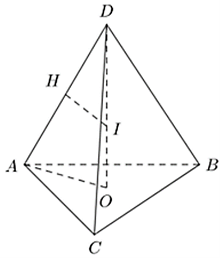
Gọi \(O\) là tâm đường tròn ngoại tiếp đáy \(ABC.\)
Do \(DA = DB = DC\) nên \(DO \bot \left( {ABC} \right).\)
Gọi \[H\] là trung điểm \(DA.\) Qua \[H\] kẻ \(HI \bot DA\,\,\left( {I \in DO} \right).\)
Khi đó \(I\) là tâm mặt cầu ngoại tiếp tứ diện.
− Xét tam giác \(ABC\) có:
• \(\cos \widehat {ACB} = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2 \cdot AC \cdot BC}} = \frac{{{a^2} + {a^2} - \frac{{3{a^2}}}{4}}}{{2 \cdot a \cdot a}} = \frac{5}{8}\)
\( \Rightarrow \sin \widehat {ACB} = \frac{{\sqrt {39} }}{8}\).− Xét tam giác \(OAD\) vuông tại \(O\) nên \[OD = \sqrt {A{D^2} - O{A^2}} = \sqrt {{a^2} - {{\left( {\frac{{2a\sqrt {13} }}{{13}}} \right)}^2}} = \frac{{3a\sqrt {13} }}{{13}}.\]
Ta có \(\Delta DHI = \Delta D{\rm{OA}}\,\,{\rm{(g}}{\rm{.g)}}\) suy ra \(DI = \frac{{DH \cdot DA}}{{DO}} = \frac{{D{A^2}}}{{2DO}} = \frac{{{a^2}}}{{2 \cdot \frac{{3\sqrt {13} }}{{13}}}} = \frac{{a\sqrt {13} }}{6}\).
Suy ra bán kính mặt cầu ngoại tiếp tứ diện \(ABCD\) bằng \(R = \frac{{a\sqrt {13} }}{6}\).
\( \Rightarrow m = 13\,,\,\,n = 6 \Rightarrow T = m + n = 19.\)
Đáp án: 19.
Câu 42:

 Xem đáp án
Xem đáp án
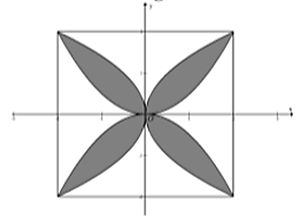
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng \[10\,\,cm = 1\,\,dm)\], các cánh hoa tạo bởi các đường parabol có phương trình
\(y = \frac{{{x^2}}}{2},\,\,y = - \frac{{{x^2}}}{2},\,\,x = - \frac{{{y^2}}}{2},\,\,x = \frac{{{y^2}}}{2}.\)
Diện tích một cánh hoa (nằm trong góc phần tư thứ nhất) bằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = \frac{{{x^2}}}{2},\,\,y = \sqrt {2x} \) và hai đường thẳng \(x = 0\,,\,\,x = 2.\)Do đó diện tích một cánh hoa bằng
\(\int\limits_0^2 {\left( {\sqrt {2x} - \frac{{{x^2}}}{2}} \right)dx} = \left. {\left[ {\frac{{2\sqrt 2 }}{3}\sqrt {{{\left( {2x} \right)}^3}} - \frac{{{x^3}}}{6}} \right]} \right|_0^2 = \frac{4}{3}\,\,\left( {{\rm{d}}{{\rm{m}}^2}} \right) = \frac{{400}}{3}\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right){\rm{. }}\)
Đáp án: \[\frac{{400}}{3}\].
Câu 43:
 Xem đáp án
Xem đáp án
Giả sử \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) và \(w = x + yi\,\,\left( {x,\,y \in \mathbb{R}} \right)\)
Ta có \(\left( {z - 2 + i} \right)\left( {\bar z - 2 - i} \right) = 25\)
\( \Leftrightarrow \left[ {a - 2 + \left( {b + 1} \right)i} \right]\left[ {a - 2 - \left( {b + 1} \right)i} \right] = 25 \Leftrightarrow {\left( {a - 2} \right)^2} + {\left( {b + 1} \right)^2} = 25\).
Theo giả thiết: \[{\rm{w}} = 2\bar z - 2 + 3i \Leftrightarrow x + yi = 2\left( {a - bi} \right) - 2 + 3i\]
\( \Leftrightarrow x + yi = 2a - 2 + \left( {3 - 2b} \right)i \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2a - 2}\\{y = 3 - 2b}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{{x + 2}}{2}}\\{b = \frac{{3 - y}}{2}}\end{array}} \right.} \right.\).
Thay (2) vào (1) ta được \({\left( {\frac{{x + 2}}{2} - 2} \right)^2} + {\left( {\frac{{3 - y}}{2} + 1} \right)^2} = 25 \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 5} \right)^2} = 100.\)
Suy ra, tập hợp điểm biểu diễn của số phức \[w\] là đường tròn tâm \(I\left( {2\,;\,\,5} \right)\) và bán kính \(R = 10.\)
Vậy \(a + b + c = 17.\)
Đáp án: 17.
Câu 44:
 Xem đáp án
Xem đáp án
Phương trình đoạn chắn của mặt phẳng \(\left( {ABC} \right)\) là: \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1.\)
Vì điểm \(M\left( {\frac{1}{7};\frac{2}{7};\frac{3}{7}} \right)\) thuộc mặt phẳng \(\left( {ABC} \right)\) nên
\(\frac{{\frac{1}{7}}}{a} + \frac{{\frac{2}{7}}}{b} + \frac{{\frac{3}{7}}}{c} = 1 \Rightarrow \frac{1}{{7a}} + \frac{2}{{7b}} + \frac{3}{{7c}} = 1 \Rightarrow \frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7\).
Mặt khác mặt phẳng \(\left( {ABC} \right)\) tiếp xúc với \((S):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{72}}{7}\)
Do đó, khoảng cách từ tâm \[I\left( {1\,;\,\,2\,;\,\,3} \right)\] của cầu tới mặt phẳng \(\left( {ABC} \right)\) là \(\sqrt {\frac{{72}}{7}} \)
\( \Rightarrow d\left( {I\,,\,\,\left( {ABC} \right)} \right) = \frac{{\left| {\frac{1}{a} + \frac{2}{b} + \frac{3}{c} - 1} \right|}}{{\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} }} = \sqrt {\frac{{72}}{7}} \) mà \(\frac{1}{a} + \frac{2}{b} + \frac{3}{c} = 7\)
\( \Rightarrow d\left( {I\,,\,\,\left( {ABC} \right)} \right) = \frac{{\left| {7 - 1} \right|}}{{\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} }} = \sqrt {\frac{{72}}{7}} \Rightarrow \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{7}{2}{\rm{.}}\) Đáp án: \[\frac{7}{2}\].
Câu 45:
Cho tứ diện \[ABCD\], trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \frac{3}{2}BN,\,\,AC = 2AP.\) Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \[ABCD\] thành hai phần có thể tích là \({V_1},\,\,{V_2}\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}.\)
 Xem đáp án
Xem đáp án
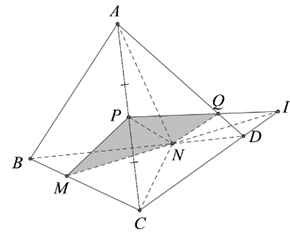
Gọi Ta có \[Q = AD \cap \left( {MNP} \right).\]
Thiết diện \[ABCD\] được cắt bởi mặt phẳng \[\left( {MNP} \right)\] là tứ giác \(MNQP\).
Áp dụng định lsi Menelaus trong các tam giác \(BCD\) và \(ACD\), ta có:\(\frac{{NB}}{{ND}} \cdot \frac{{ID}}{{IC}} \cdot \frac{{MC}}{{MB}} = 1 \Rightarrow \frac{{ID}}{{IC}} = \frac{1}{4}\) và \[\frac{{ID}}{{IC}} \cdot \frac{{PC}}{{PA}} \cdot \frac{{QA}}{{QD}} = 1 \Rightarrow \frac{{QA}}{{QD}} = 4\].\[{V_{ABCD}} = V,\,\,I = MN \cap CD,\,\,Q = IP \cap AD.\]
Áp dụng bài toán tỉ số thể tích của hai khối chóp tam giác, ta có
•\[\frac{{{V_{ANPQ}}}}{{{V_{ANCD}}}} = \frac{{AP}}{{AC}} \cdot \frac{{AQ}}{{AD}} = \frac{2}{5}\]\( \Rightarrow {V_{ANPQ}} = \frac{2}{5}{V_{ANCD}} = \frac{2}{{15}}V\) suy ra \({V_{N.PQDC}} = \frac{1}{3}V - \frac{2}{{15}}V = \frac{1}{5}V\);
• \[\frac{{{V_{CMNP}}}}{{{V_{CBNA}}}} = \frac{{CM}}{{CB}} \cdot \frac{{CP}}{{CA}} = \frac{1}{3} \Rightarrow {V_{CMNP}} = \frac{1}{3}{V_{CBNA}} = \frac{2}{9}V\] suy ra \({V_2} = {V_{N.PQDC}} + {V_{CMNP}} = \frac{{19}}{{45}}V.\)
Do đó \({V_1} = V - {V_2} = \frac{{26}}{{45}}V.\) Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{{26}}{{19}}.\)
Đáp án: \[\frac{{26}}{{19}}\].
Câu 46:
 Xem đáp án
Xem đáp án
Đặt \(w = z - 2\), ta được phương trình \({\left( {w + 2} \right)^2} - 2m\left( {w + 2} \right) + 2{m^2} - 2m = 0\)
\( \Leftrightarrow {w^2} - (2m - 4)w + 2{m^2} - 6m + 4 = 0\).
Khi đó bài toán trở thành tìm \(m\) để phương trình (1) có hai nghiệm phân biệt \({w_1},{w_2}\) thỏa mãn \(\left| {{w_1}} \right| = \left| {{w_2}} \right|.\)
Xét phương trình (1) có \(\Delta ' = {\left( {m - 2} \right)^2} - 2{m^2} + 6m - 4 = - {m^2} + 2m.\)
• TH1: \(\Delta ' > 0 \Leftrightarrow m \in \left( {0\,;\,\,2} \right).\) Mà \(m \in \mathbb{Z}\) nên \(m = 1.\)
Thay vào phương trình ta được \({w^2} + 2w = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{w = 0}\\{w = - 2}\end{array}} \right.\) không thỏa mãn yêu cầu đề bài.
• TH2: \(\Delta ' < 0 \Leftrightarrow m \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right).\)
Khi đó phương trình luôn có hai nghiệm phức phân biệt không phải số thực, hai nghiệm này là hai số phức liên hợp nên mô-đun của chúng luôn bằng nhau.
Kết hợp với điều kiện \(m\) là số nguyên và \(m \in \left( { - 10\,;\,\,10} \right)\).
Suy ra \(m \in \left\{ { - 9\,;\,\, - 8\,;\,\, \ldots \,;\,\, - 1} \right\} \cup \left\{ {3\,;\,\,4\,;\,\, \ldots \,;\,\,9} \right\}.\)
Vậy có 16 giá trị của \(m\) thỏa mãn. Đáp án: 6.
Câu 47:
Cho mặt phẳng \((\alpha ):2x + 6y - 3z - 1 = 0\) và ba điểm \[A\left( {1\,;\,\, - 1\,;\,\, - 5} \right),\,\,B\left( {0\,;\,\,1\,;\,\,2} \right),\,\]\[\,C\left( {2\,;\,\,3\,;\,\, - 1} \right).\] Biết điểm \(M\) thuộc mặt phẳng \((\alpha )\) sao cho \(P = M{A^2} + 2M{B^2} - 2M{C^2}\) đạt giá trị nhỏ nhất là \({P_{\min }}.\) Khi đó \({P_{\min }}\) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi \(I\left( {a\,;\,b\,;\,c} \right)\) sao cho \(\overrightarrow {IA} + 2\overrightarrow {IB} - 2\overrightarrow {IC} = \vec 0.\)
\( \Rightarrow \overrightarrow {OI} = \overrightarrow {OA} + 2\overrightarrow {OB} - 2\overrightarrow {OC} \Rightarrow I\left( { - 3\,;\,\, - 5\,;\,\, - 3} \right)\).
Ta có \(P = M{A^2} + 2M{B^2} - 2M{C^2} = {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + 2{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} - 2{\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2}\)
\( = M{I^2} + I{A^2} + 2I{B^2} - 2I{C^2} + 2\left( {\overrightarrow {IA} + 2\overrightarrow {IB} - 2\overrightarrow {IC} } \right) = M{I^2} + I{A^2} + 2I{B^2} - 2I{C^2}{\rm{. }}\)
Do \(I{A^2} + 2I{B^2} - 2I{C^2} = 36 + 70 - 93 = 13\) không đổi nên \({P_{\min }} \Leftrightarrow M{I_{\min }}\)
Và \[M{I_{\min }} = {\rm{d}}\left( {I,\,\,\left( P \right)} \right) = \frac{{\left| {2 \cdot \left( { - 3} \right) + 6 \cdot \left( { - 5} \right) - 3 \cdot \left( { - 3} \right) - 1} \right|}}{{\sqrt {4 + 36 + 9} }} = 4.\]
Vậy \({P_{\min }} = 4 + 13 = 17.\) Đáp án: 17.
Câu 48:
Có bao nhiêu cặp số nguyên \(\left( {x\,;\,\,y} \right)\) thỏa mãn đồng thời \({2^x} + y \le {\log _2}(x - y)\) và \[x,\,\,y\] thuộc đoạn \(\left[ { - 2\,;\,\,10} \right]\)?
 Xem đáp án
Xem đáp án
Ta có \({2^x} + y \le {\log _2}\left( {x - y} \right)\)
\( \Leftrightarrow {2^x} + x \le {\log _2}\left( {x - y} \right) \Leftrightarrow {2^x} + x \le {\log _2}\left( {x - y} \right) + {2^{{{\log }_2}\left( {x - y} \right)}}\)
• Xét hàm số \(f(t) = {2^t} + t\) có \(f'\left( t \right) = {2^t}\ln 2 + 1 > 0,\,\,\forall t \in \mathbb{R}.\)
Hàm số đồng biến trên \(\mathbb{R}\), do đó: \((*) \Leftrightarrow x \le {\log _2}\left( {x - y} \right) \Leftrightarrow {2^x} \le x - y \Leftrightarrow y \le x - {2^x}\,\,(**)\)
• Xét hàm số \(g(x) = x - {2^x}\) trên đoạn \(\left[ { - 2\,;\,\,10} \right]\).
Ta có: \(g'\left( x \right) = 1 - {2^x}\ln 2\) và \(g'\left( x \right) = 0 \Leftrightarrow x = {\log _2}\left( {{{\log }_2}e} \right)\)
Bảng biến thiên
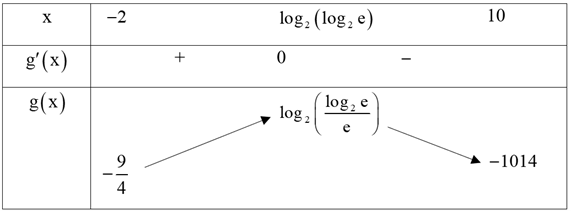
Kết hợp \((**)\) và bảng biên thiên ta có: \( - 2 \le y \le {\log _2}\left( {\frac{{{{\log }_2}e}}{e}} \right)\).
Do \(y \in \mathbb{Z}\) nên \(y = - 2\) hoặc \(y = - 1\).
• Với \(y = - 2\) ta có: \(g\left( x \right) \ge - 2.\) Do \(x \in \mathbb{Z}\) nên suy ra \(x \in \left\{ { - 1\,;\,\,0\,;\,\,1\,;\,\,2} \right\}.\)
Trường hợp này có bốn cặp số \(\left( {x\,;\,\,y} \right)\) thỏa mãn.
• Với \(y = - 1\) ta có: \(g\left( x \right) \ge - 1.\) Do \(x \in \mathbb{Z}\) nên suy ra \(x \in \left\{ {0\,;\,\,1} \right\}.\)
Trường hợp này có hai cặp số \(\left( {x\,;\,\,y} \right)\) thỏa mãn.
Vậy có tất cả 6 cặp số \(\left( {x\,;\,\,y} \right)\) thỏa mãn yêu cầu bài toán.
Đáp án: 6.
Câu 49:
 Xem đáp án
Xem đáp án
Điều kiện: \(x \le 1.\)
\({\rm{Ta c\'o }}2{y^3} + 7y + 2x\sqrt {1 - x} = 3\sqrt {1 - x} + 3\left( {2{y^2} + 1} \right)\)
\( \Leftrightarrow 2\left( {{y^3} - 3{y^2} + 3y - 1} \right) + y - 1 = 2\sqrt {1 - x} \left( {1 - x} \right) + \sqrt {1 - x} \)
\( \Leftrightarrow 2{\left( {y - 1} \right)^3} + y - 1 = 2{\left( {\sqrt {1 - x} } \right)^3} + \sqrt {1 - x} \,\,\,(*)\)
Xét hàm số \(f\left( t \right) = 2{t^3} + t\) có \(f'\left( t \right) = 6{t^2} + 1 > 0,\,\,\forall t \in \mathbb{R}\), suy ra \(f\left( t \right)\) đồng biến trên \(\mathbb{R}.\)
Khi đó \((*) \Leftrightarrow f\left( {y - 1} \right) = f\left( {\sqrt {1 - x} } \right) \Leftrightarrow y - 1 = \sqrt {1 - x} \Leftrightarrow x = 2y - {y^2}\) (điều kiện \(y \ge 1\))
Khi đó \[P = x + 2y = - {y^2} + 4y = 4 - {\left( {y - 2} \right)^2} \le 4\]
Đẳng thức xảy ra khi \(y = 2,x = 0.\)
Vậy \(\max P = 4\) khi \(\left( {x\,;\,\,y} \right) = \left( {0\,;\,\,2} \right).\)
Đáp án: 4.
Câu 50:
Cho hình thang \[ABCD\] vuông tại \(A\) tại \(B\) có \(AB = 1\,,\,\,AD = 3\) và \(BC = x\) với \(0 < x < 3.\) Gọi \({V_1},{V_2}\) lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình thang \[ABCD\] (kể cả các điểm trong) quanh đường thẳng \[BC\] và \[AD.\] Tìm \[x\] để \(\frac{{{V_1}}}{{{V_2}}} = \frac{7}{5}\).
 Xem đáp án
Xem đáp án
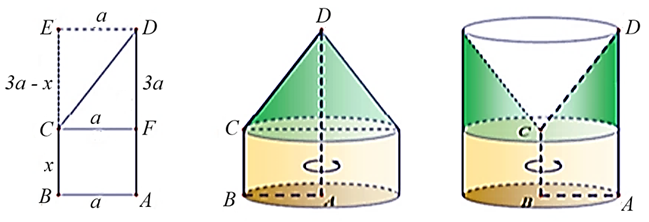
Dựng các điểm \[E,\,\,F\] để có các hình chữ nhật \[ABED\] và \[ABCF\] như hình vẽ.
• TH1: Khi quay hình thang \[ABCD\] (kể cả các điểm trong) quanh đường thẳng \[BC\] ta được khối tròn xoay có thể tích là \({V_1} = {V_3} - {V_4} = 3\pi - \frac{1}{3}\pi \left( {3 - x} \right) = 2\pi + \frac{1}{3}\pi x = \frac{1}{3}\pi \left( {6 + x} \right).\)
Trong đó, \({V_3}\) là thể tích khối trụ tròn xoay có bán kính đáy bằng 1 , chiều cao bằng \(3;{V_4}\) là thể tích khối nón tròn xoay có bán kính đáy bằng 1, chiều cao bằng \(3 - x.\)
• TH2: Khi quay hình thang \[ABCD\] (kể cả các điểm trong) quanh đường thẳng \[AD\] ta được khối tròn xoay có thể tích là \({V_2} = {V_5} + {V_4} = \pi x + \frac{1}{3}\pi \left( {3 - x} \right) = \pi + \frac{2}{3}\pi x = \frac{1}{3}\pi \left( {3 + 2x} \right).\)
Trong đó, \({V_5}\) là thể tích khối trụ tròn xoay có bán kính đáy bằng 1 , chiều cao bằng x.
Theo giả thiết ta có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{7}{5} \Leftrightarrow \frac{{6 + x}}{{3 + 2x}} = \frac{7}{5} \Leftrightarrow x = 1.\)
Đáp án: 1.
Câu 51:
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Theo tác giả đoạn trích, người Việt Nam có “sở trường” nhất ở ngành nghệ thuật nào?
 Xem đáp án
Xem đáp án
Câu 52:
Phong cách ngôn ngữ của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Phong cách ngôn ngữ của đoạn trích là khoa học. Trong đoạn trích sử dụng nhiều thuật ngữ khoa học cùng với nội dung mang tính chất nghiên cứu khoa học. Chọn D.
Câu 53:
 Xem đáp án
Xem đáp án
Câu 55:
 Xem đáp án
Xem đáp án
Câu 56:
Phương thức biểu đạt chính của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Phương thức biểu đạt chính của đoạn trích là tự sự. Chọn B.
Câu 57:
 Xem đáp án
Xem đáp án
Nhân vật Nghĩa không xuất hiện trực tiếp trong đoạn trích. Chọn C.
Câu 58:
 Xem đáp án
Xem đáp án
Câu 59:
 Xem đáp án
Xem đáp án
Câu 60:
 Xem đáp án
Xem đáp án
Câu 61:
Ý nào sau đây KHÔNG được nói đến trong đoạn trích?
 Xem đáp án
Xem đáp án
Câu 62:
 Xem đáp án
Xem đáp án
Câu 63:
 Xem đáp án
Xem đáp án
Biện pháp tu từ: Nhân hóa: Cái tư tưởng - tư tưởng náu mình, yên lặng. Chọn B.
Câu 64:
 Xem đáp án
Xem đáp án
Câu 65:
 Xem đáp án
Xem đáp án
Câu 66:
 Xem đáp án
Xem đáp án
Câu 67:
 Xem đáp án
Xem đáp án
Câu 68:
 Xem đáp án
Xem đáp án
Câu 69:
 Xem đáp án
Xem đáp án
Câu 70:
 Xem đáp án
Xem đáp án
Câu 71:
 Xem đáp án
Xem đáp án
Câu 72:
 Xem đáp án
Xem đáp án
Câu 73:
 Xem đáp án
Xem đáp án
Câu 74:
 Xem đáp án
Xem đáp án
Câu 75:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Càng lớn lên tôi càng thấy việc học trở nên nghiêm trọng, những kiến thức ngày một nhiều khiến tôi đang rất mơ hồ.
 Xem đáp án
Xem đáp án
Câu 76:
 Xem đáp án
Xem đáp án
Câu 77:
 Xem đáp án
Xem đáp án
Câu 78:
 Xem đáp án
Xem đáp án
Câu 79:
 Xem đáp án
Xem đáp án
Câu 80:
 Xem đáp án
Xem đáp án
Câu 81:
 Xem đáp án
Xem đáp án
Câu 82:
 Xem đáp án
Xem đáp án
Câu 83:
 Xem đáp án
Xem đáp án
Câu 84:
 Xem đáp án
Xem đáp án
Câu 85:
 Xem đáp án
Xem đáp án
Câu 86:
 Xem đáp án
Xem đáp án
Câu 87:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tôi nhớ me tôi, thuở thiếu thời
Lúc người còn sống tôi lên mười
Mỗi lần nắng mới reo ngoài nội
Áo đỏ người đưa trước dậu phơi.
(Nắng mới – Lưu Trọng Lư)
 Xem đáp án
Xem đáp án
Câu 88:
Mau đi thôi! Mùa chưa ngả chiều hôm,
Ta muốn ôm
Cả sự sống mới bắt đầu mơn mởn;
Ta muốn riết mây đưa và gió lượn,
Ta muốn say cánh bướm với tình yêu,
Ta muốn thâu trong một cái hôn nhiều
Và non nước, và cây, và cỏ rạng,
Cho chếnh choáng mùi thơm, cho đã đầy ánh sáng
Cho no nê thanh sắc của thời tươi;
– Hỡi xuân hồng, ta muốn cắn vào ngươi!
(Vội vàng – Xuân Diệu)
 Xem đáp án
Xem đáp án
Câu 89:
Đọc đoạn trích sau và trả lời câu hỏi:
Ban trưởng nhà lao chuyên đánh bạc,
Giải người, cảnh trưởng kiếm ăn quanh;
Chong đèn, huyện trưởng làm công việc,
Trời đất Lai Tân vẫn thái bình.
(Lai Tân – Hồ Chí Minh)
 Xem đáp án
Xem đáp án
Câu 90:
Tại Hội thảo, Tiến sĩ Trần Thiện Khanh, Phó Viện trưởng Văn học đã đặt ra vấn đề văn học Đông Nam Á dường như chưa được hiện diện trong các công trình nghiên cứu lịch sử nghiên cứu của bộ môn văn học so sánh của thế giới.
Sự thiếu hụt này mới được những nhà nghiên cứu văn học phương Tây quan tâm, chú ý trong thời gian gần đây. Nhưng chỉ dừng lại ở việc cung cấp chất liệu cho các lí thuyết về mối quan hệ giữa văn học và các vấn đề lịch sử, chính trị, xã hội. Bởi vậy, Hội thảo này sē là dấu mốc cho sự phát triển của văn học so sánh Đông Nam Á.
(Hải Đăng, Xây dựng nghiên cứu diễn đàn văn học so sánh ở Đông Nam Á, https://nhandan.vn)
 Xem đáp án
Xem đáp án
Câu 91:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Đám than đã vạc hẳn lửa. Mị không thổi cũng không đứng lên. Mị nhớ lại đời mình. Mị tưởng tượng như có bà lão khẽ dặng hắng một tiếng, nhẹ nhàng nói với “nàng dâu mới”:
- Ừ, thôi thì các con đã phải duyên phải kiếp với nhau, u cũng mừng lòng…
Tràng thở đánh phào một cái, ngực nhẹ hẳn đi. Hắn ho khẽ một tiếng, bước từng bước dài ra sân. Bà cụ Tứ vẫn từ tốn tiếp lời:
- Nhà ta thì nghèo con ạ. Vợ chồng chúng mày liệu mà bảo nhau làm ăn. Rồi ra may mà ông giời cho khá… Biết thế nào hở con, ai giàu ba họ, ai khó ba đời? Có ra thì rồi con cái chúng mày về sau.
(Trích Vợ nhặt – Kim Lân)
Vì sao bà cụ Tứ lại nói với các con của mình là “Ừ, thôi thì các con đã phải duyên phải kiếp với nhau, u cũng mừng lòng…” thay vì “… u cũng bằng lòng”?
 Xem đáp án
Xem đáp án
Câu 92:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Quyện điểu quy lâm tầm túc thụ,
Cô vân mạn mạn độ thiên không;
Sơn thôn thiếu nữ ma bao túc,
Bao túc ma hoàn, lô dĩ hồng.
(Chiều tối – Hồ Chí Minh)
Hình ảnh “quyện điểu”, “cô vân” được sử dụng trong đoạn trích có liên hệ với nội dung gì dưới đây?
 Xem đáp án
Xem đáp án
Câu 93:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Vòng thứ hai này tăng thêm nhiều cửa tử để đánh lừa con thuyền vào, và cửa sinh được bố trí lệch qua phía bờ hữu ngạn. Cưỡi lên thác Sông Đà, phải cưỡi đến cùng như là cưỡi hổ. Dòng thác hùm beo đang hồng hộc tế mạnh trên sông đá. Nắm chặt lấy được cái bờm sóng đúng luồng rồi, ông đò ghì cương lái bám chắc lấy luồng nước đúng mà phóng nhanh vào cửa sinh, mà lái miết một đường chéo về phía cửa đá ấy. Bốn năm bọn thủy quân cửa ải nước bên bờ trái liền xô ra định níu thuyền lôi vào tập đoàn cửa tử. Ông đò vẫn nhớ mặt bọn này, đứa thì ông tránh mà rảo bơi chèo lên, đứa thì ông đè sấn lên mà chặt đôi ra để mở đường tiến.
(Người lái đò Sông Đà – Nguyễn Tuân)
Nội dung chính của đoạn trích trên là gì?
 Xem đáp án
Xem đáp án
Câu 94:
Đọc đoạn trích sau và trả lời câu hỏi:
Vũ Như Tô (đầy hi vọng) - Dẫn ta ra mắt An Hòa Hầu, để ta phân trần, để ta giảng giải, cho người đời biết rõ nguyện vọng của ta. Ta tội gì. Không, ta chỉ có một hoài bão là tô điểm cho đất nước, đem hết tài ra xây cho giống nòi một tòa đài hoa lệ, thách cả những công trình sau trước, tranh tinh xảo với hóa công. Vậy thì ta có tội gì? Ta xây Cửu Trùng Đài có phải đâu để hại nước? Không, không, Nguyễn Hoằng Dụ sẽ biết cho ta, ta không có tội và chủ tướng các ngươi sẽ cởi trói cho ta để ta xây nốt Cửu Trùng Đài, dựng một kì công muôn thuở…
(Vĩnh biệt Cửu Trùng Đài – Nguyễn Huy Tưởng)
Qua lời nói của nhân vật Vũ Như Tô, hình tượng Cửu Trùng Đài mang ý nghĩa gì?
 Xem đáp án
Xem đáp án
Câu 95:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trong cửa hàng hơi tối, muỗi đã bắt đầu vo ve. Liên ngồi yên lặng bên mấy quả thuốc sơn đen; đôi mắt chị bóng tối ngập đầy dần và cái buồn của buổi chiều quê thấm thía vào tâm hồn ngây thơ của chị; Liên không hiểu sao, nhưng chị thấy lòng buồn man mác trước cái giờ khắc của ngày tàn.
(Hai đứa trẻ – Thạch Lam)
Đoạn trích thể hiện phẩm chất gì của nhân vật Liên?
 Xem đáp án
Xem đáp án
Câu 96:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Hôm ấy hắn láng máng nghe người ta nói họ là Việt Minh đấy. Họ đi cướp thóc đấy. Tràng không hiểu gì sợ quá, kéo vội xe thóc của Liên đoàn tắt cánh động đi lối khác. À ra họ đi phá kho thóc chia cho người đói. Tự dưng hắn thấy ân hận, tiếc rẻ vẩn vơ, khó hiểu.
Ngoài đình tiếng trống thúc thuế vẫn dồn dập. Mẹ và vợ Tràng đã buông đũa đứng dậy.
Trong óc Tràng vẫn thấy đám người đói và lá cờ đỏ bay phấp phới…
(Trích Vợ nhặt – Kim Lân)
Hình ảnh đám người đói và lá cờ đỏ bay phấp phới ở cuối bài thể hiện điều gì?
 Xem đáp án
Xem đáp án
Câu 97:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Dẫu xuôi về phương Bắc
Dẫu ngược về phương Nam
Nơi nào em cũng nghĩ
Hướng về anh – một phương
(Sóng – Xuân Quỳnh)
Những biện pháp tu từ nào được sử dụng trong đoạn trích trên?
 Xem đáp án
Xem đáp án
Câu 98:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Nhớ người mẹ nắng cháy lưng
Địu con lên rẫy, bẻ từng bắp ngô.
(Việt Bắc – Tố Hữu)
Nội dung hai câu thơ trên là gì?
 Xem đáp án
Xem đáp án
Câu 99:
Đọc đoạn trích sau và trả lời câu hỏi:
Làm trai phải lạ ở trên đời,
Há để càn khôn tự chuyển dời.
Trong khoảng trăm năm cần có tớ,
Sau này muôn thuở, há không ai?
(Lưu biệt khi xuất dương – Phan Bội Châu)
Câu thơ “Há để càn khôn tự chuyển dời” có ý nghĩa gì?
 Xem đáp án
Xem đáp án
Câu 100:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Nhà nước ba năm mở một khoa,
Trường Nam thi lẫn với trường Hà.
Lôi thôi sĩ tử vai đeo lọ,
Ậm oẹ quan trường miệng thét loa.
Lọng cắm rợp trời quan sứ đến
Váy lê quét đất mụ đầm ra.
Nhân tài đất Bắc nào ai đó?
Ngoảnh cổ mà trông cảnh nước nhà.
(Vịnh khoa thi hương – Trần Tế Xương)
Phong cách ngôn ngữ của văn bản là gì?
 Xem đáp án
Xem đáp án
Phong cách ngôn ngữ của văn bản là nghệ thuật. Chọn A.
Câu 101:
PHẦN 3: KHOA HỌC
Lĩnh vực: Khoa học tự nhiên và xã hội (50 câu – 60 phút)
Thực dân Pháp tiến hành cuộc khai thác thuộc địa lần thứ hai (1919-1929) ở Việt Nam trong bối cảnh nào sau đây?
 Xem đáp án
Xem đáp án
Câu 102:
Mục đích của thực dân Pháp khi tiến hành chương trình khai thác lần thứ nhất (1897-1914) ở Việt Nam là
 Xem đáp án
Xem đáp án
Câu 103:
 Xem đáp án
Xem đáp án
Câu 104:
 Xem đáp án
Xem đáp án
Dùng phương pháp loại trừ:
Tân Việt Cách mạng đảng đến năm 1928 không theo khuynh hướng vô sản.
Đảng Cộng sản Việt Nam năm 1930 mới ra đời.
Tâm tâm xã và Cộng sản đoàn theo khuynh hướng vô sản những có hoạt động tiêu biểu và đại diện nhất cho cho khuynh hướng cách mạng vô sản ở Việt Nam (1919-1928) là Hội Việt Nam Cách mạng Thanh niên. Chọn C.
Câu 105:
 Xem đáp án
Xem đáp án
Mĩ vừa phát động cuộc Chiến tranh lạnh năm 1947.
Hiệp định Pari về Việt Nam được kí kết năm 1973.
Liên minh châu Âu đã ra đời và phát triển năm 1991.
Hiệp hội các quốc gia Đông Nam Á (ASEAN) được thành lập năm 1967 đây là thời gian mà Mĩ đang đẩy mạnh xâm lược Việt Nam (1954-1975). Chọn A.
Câu 106:
 Xem đáp án
Xem đáp án
Phong trào công nhân Việt Nam những năm 1925-1929 chịu ảnh hưởng nhiều từ những hoạt động của Hội Việt Nam Cách mạng thanh niên nên đã dần chuyển từ tự phát sang tự giác, phong trào công nhân trở thành nòng cốt của phong trào dân tộc trong cả nước, nổ ra tại các trung tâm kinh tế, chính trị (bãi công của công nhân than Mạo Khê, nhà máy cưa Bến Thủy, xi măng Hải Phòng,...). Phong trào công nhân đã thể hiện được ý thức chính trị và ý thức của giai cấp, đấu tranh với mục tiêu dân tộc, dân chủ rõ ràng hơn. Chọn B.
Câu 107:
 Xem đáp án
Xem đáp án
Câu 108:
 Xem đáp án
Xem đáp án
Hiệp định về chấm dứt chiến tranh, lập lại hòa bình ở Việt Nam được kí chính thức ngày 27-1-1973 tại Pari giữa bốn ngoại trưởng, đại diện cho các chính phủ tham dự Hội nghị và bắt đầu có hiệu lực. Chọn C.
Câu 109:
 Xem đáp án
Xem đáp án
Câu 110:
 Xem đáp án
Xem đáp án
Câu 111:
 Xem đáp án
Xem đáp án
Câu 112:
 Xem đáp án
Xem đáp án
Câu 113:
 Xem đáp án
Xem đáp án
Câu 114:
 Xem đáp án
Xem đáp án
Câu 115:
 Xem đáp án
Xem đáp án
Câu 116:
Cho bảng số liệu:
LAO ĐỘNG PHÂN THEO KHU VỰC KINH TẾ NƯỚC TA, GIAI ĐOẠN 2009-2019
(Đơn vị: Nghìn người)
|
Năm |
2009 |
2013 |
2017 |
2019 |
|
Khu vực I |
24606,0 |
24399,3 |
21458,7 |
18831,4 |
|
Khu vực II |
9561,6 |
11086,0 |
14104,5 |
16456,7 |
|
Khu vực III |
13576,0 |
16722,5 |
18145,1 |
19371,1 |
(Nguồn: Niên giám thống kê 2019, NXB Thống kê, 2020)
Theo bảng số liệu, để thể hiện tốc độ tăng trưởng lao động phân theo khu vực kinh tế nước ta giai đoạn 2009-2019, dạng biểu đồ nào sau đây là thích hợp nhất?
 Xem đáp án
Xem đáp án
Câu 117:
 Xem đáp án
Xem đáp án
Câu 118:
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
- Đáp án A. nước ta có điều kiện thuận lợi để phát triển ngành đường biển. → đây là yếu tố có sẵn từ trước, không thúc đẩy ngành vận tải đường biển phát triển nhanh.
- Đáp án B. nước ta đang thực hiện mở cửa, quan hệ quốc tế ngày càng tăng. → đúng. Chọn B.
- Đáp án C. ngành dầu khi phát triển mạnh, vận chuyển chủ yếu bằng đường biển. → đúng nhưng chưa đủ, không chỉ ngành dầu khi phát triển mà còn nhiều ngành khác.
- Đáp án D. ngoại thương nước ta phát triển mạnh, lượng hàng xuất nhập khẩu lớn. → không bao quát bằng B
Câu 119:
 Xem đáp án
Xem đáp án
Câu 120:
 Xem đáp án
Xem đáp án
Câu 121:
Cách biểu diễn lực tương tác giữa hai điện tích đứng yên trường hợp nào sau đây là sai?

 Xem đáp án
Xem đáp án
Khi cho hai điện tích cùng loại lại gần nhau thì chúng đẩy nhau. Chọn B.
Câu 122:
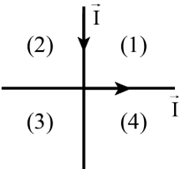
 Xem đáp án
Xem đáp án
Vận dụng quy tắc nắm tay phải: vùng (2), (4) từ trường do hai dây dẫn gây ra có thể triệt tiêu nhau. Chọn D.
Câu 123:
Một dây dẫn thẳng được đặt vuông góc với mặt phẳng hình vẽ. Đường sức từ quay ngược chiều kim đồng hồ. Chiều đi của dòng điện là
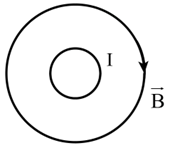
 Xem đáp án
Xem đáp án
Vận dụng quy tắc nắm tay phải ta thấy dòng điện có chiều đi vào mặt phẳng.
Chọn A.
Câu 124:
 Xem đáp án
Xem đáp án
Tia tử ngoại có có tác dụng diệt khuẩn do vậy nó có thể diệt được 99% vi khuẩn.
Chọn B.
Câu 125:
Ở Hà Nội, một sóng điện từ truyền theo phương thẳng đứng chiều từ dưới lên. Tại một điểm nhất định trên phương truyền sóng, khi vectơ cảm ứng từ hướng về phía Nam thì vecto cường độ điện trường hướng về phía nào?
 Xem đáp án
Xem đáp án
Câu 126:
 Xem đáp án
Xem đáp án
Gọi V là thể tích máu của người đó. Độ phóng xạ H = 597.V (phân rã/phút) = 9,95.V (Bq). Ta có: \({\rm{H}} = {{\rm{H}}_0}{2^{ - \frac{{\rm{t}}}{{\rm{T}}}}} \Rightarrow \frac{{9,95\;{\rm{V}}}}{{74000}} = {2^{ - \frac{{3,75}}{{15}}}} \Rightarrow {\rm{V}} = 6253,9\;{\rm{c}}{{\rm{m}}^3} = 6,25\)lít. Chọn B.
Câu 127:
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi nhưng tần số thay đổi được vào hai đầu đoạn mạch AB gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C mắc nối tiếp như hình vẽ. Đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng giữa hai đầu đoạn mạch AN (đường màu đỏ) và điện áp hiệu dụng giữa hai đầu đoạn mạch MN (đường màu đen) theo giá trị tần số góc \[{\rm{\omega }}\] như hình vẽ. Khi \[{\rm{\omega }} = y\] thì hệ số công suất của đoạn mạch AB có giá trị nào sau đây?
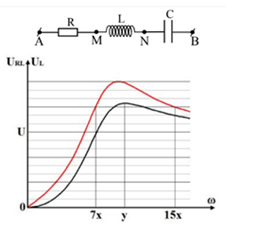
Làm tròn đến chữ số thập phân thứ nhất.
Đáp án: ……….
 Xem đáp án
Xem đáp án
Ta có, khi UAN cực đại thì:
\({U_{AN}} = {U_{RL}} = \frac{{U.\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{U.\sqrt {{R^2} + {{({\rm{\omega }}L)}^2}} }}{{\sqrt {{R^2} + {{\left( {{\rm{\omega }}L - \frac{1}{{{\rm{\omega }}C}}} \right)}^2}} }} = \frac{U}{{\sqrt {1 - {p^{ - 2}}} }} \cdot \) Với \(p = \frac{1}{2}\left( {1 + \sqrt {1 + 2\frac{{{R^2}C}}{L}} } \right)\)
Từ đồ thị ta thấy \({{\rm{U}}_{{\rm{AN}}}} = \frac{5}{3}{\rm{U}} \Rightarrow {\rm{p}} = 1,25 \Rightarrow \frac{{{{\rm{R}}^2}{\rm{C}}}}{{\rm{L}}} = 0,625\)
Tại \({\rm{\omega }} = y\) thì \({U_{L\max }}\), ta có: \(\left\{ {\begin{array}{*{20}{l}}{{Z_C} = \sqrt {\frac{L}{C} - \frac{{{R^2}}}{2}} }\\{{Z_L} = \frac{L}{C}.\frac{1}{{{Z_C}}}}\end{array} \Rightarrow \frac{{{Z_L}}}{{{Z_C}}} = \frac{L}{C}.\frac{1}{{\frac{L}{C} - \frac{{{R^2}}}{2}}} = \frac{1}{{1 - \frac{{{R^2}C}}{L}}} = 1,455} \right.\)
Chuẩn hóa số liệu: \({Z_C} = 1;{Z_L} = 1,455;R = 0,95\)
Hệ số công suất: \(\cos {\rm{\varphi }} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{0,95}}{{\sqrt {0,{{95}^2} + {{(1,455 - 1)}^2}} }} = 0,9\). Đáp án. 0,9.
Câu 128:
Trong thí nghiệm khe Y–âng ta thu được hệ thống vân sáng, vân tối trên màn. Xét hai điểm A, B đối xứng qua vân trung tâm, khi màn cách mặt phẳng chứa hai khe một khoảng là D thì A, B là vân sáng. Dịch chuyển màn ra xa hai khe một khoảng d thì A, B là vân sáng và đếm được số vân sáng trên đoạn AB trước và sau dịch chuyển màn hơn kém nhau 4. Nếu dịch tiếp màn ra xa hai khe một khoảng 9d nữa thì A, B là vân sáng và nếu dịch tiếp màn ra xa nữa thì tại A và B không còn xuất hiện vân sáng nữa. Tại A khi chưa dịch chuyển màn là vân sáng thứ mấy?
 Xem đáp án
Xem đáp án
Giả sử ban đầu A là vị trí cho vân sáng bậc \(k \to {x_M} = k\frac{{D{\rm{\lambda }}}}{a}\) (1)
Khi dịch chuyển màn ra xa một đọan d thì A vẫn là vân sáng nhưng số vân sáng trên AB giảm đi 4 vân điều này chứng tỏ tại A lúc này là vân sáng bậc \(\left( {{\rm{k}} - 2} \right)\)\( \to {{\rm{x}}_{\rm{M}}} = ({\rm{k}} - 2)\frac{{({\rm{D}} + {\rm{d}}){\rm{\lambda }}}}{{\rm{a}}}\)
Từ (1) và (2): \(k\frac{{D{\rm{\lambda }}}}{a} = ({\rm{k}} - 2)\frac{{({\rm{D}} + {\rm{d}}){\rm{\lambda }}}}{{\rm{a}}} \Rightarrow \)\({\rm{k}} = ({\rm{k}} - 2)\left( {1 + \frac{{\rm{d}}}{{\rm{D}}}} \right)\)(*)
Tiếp tục dịch chuyển màn ra xa thêm một khoảng 9d nữa thì A là vân sáng, sau đó nếu dịch chuyển màn tiếp tục ra xa thì ta sẽ không thu được vân sáng nên lúc này A là vân sáng bậc nhất
\( \Rightarrow {{\rm{x}}_{\rm{M}}} = \frac{{({\rm{D}} + 10\;{\rm{d}}){\rm{\lambda }}}}{{\rm{a}}}\) (3)
Từ (1) và (3): \(k\frac{{D{\rm{\lambda }}}}{a} = \frac{{({\rm{D}} + 10\;{\rm{d}}){\rm{\lambda }}}}{{\rm{a}}} \Rightarrow {\rm{kD}} = {\rm{D}} + 10\;{\rm{d}} \Rightarrow \frac{{\rm{d}}}{{\rm{D}}} = \frac{{{\rm{k}} - 1}}{{10}}\)
Thay vào phương trình (*) ta thu được \(\frac{{{{\rm{k}}^2}}}{{10}} - \frac{3}{{10}}{\rm{k}} - \frac{9}{5} = 0 \to {\rm{k}} = 6\). Chọn D.
Câu 129:
 Xem đáp án
Xem đáp án
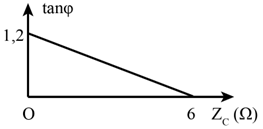
Độ lệch pha giữa u và i: \(\tan {\rm{\varphi }} = \frac{{{Z_L} - {Z_C}}}{R}\).
Từ đồ thị ta thấy khi: \({{\rm{Z}}_{\rm{C}}} = 6 \Rightarrow \tan {\rm{\varphi }} = 0 \Rightarrow \frac{{{{\rm{Z}}_{\rm{L}}} - 6}}{{\rm{R}}} = 0 \Rightarrow {{\rm{Z}}_{\rm{L}}} = 6\)
\({Z_C} = 0 \Rightarrow \tan {\rm{\varphi }} = 1,2V \Rightarrow \frac{{{Z_L}}}{R} = 1,2 \Rightarrow R = \frac{{{Z_L}}}{{1,2}} = 5\Omega \). Chọn A.
Câu 130:
 Xem đáp án
Xem đáp án
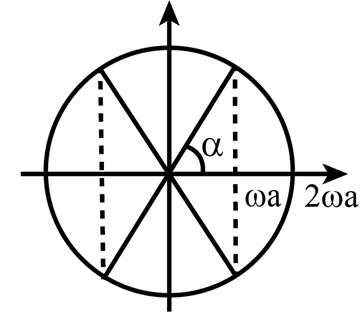
Bước sóng: \(\frac{{\rm{\lambda }}}{4} = {\rm{AB}} \Rightarrow {\rm{\lambda }} = 4.15 = 60\;\,{\rm{cm}}{\rm{.}}\)
Biên độ của M là: \({{\rm{A}}_{\rm{M}}} = \left| {2{\rm{a}}{\rm{.}}\cos \left( {2{\rm{\pi }}.\frac{{10}}{{60}}} \right)} \right| = {\rm{a}}\)
Vận tốc cực đại của phần tử M và N là \(\left\{ {\begin{array}{*{20}{l}}{{v_{M\max }} = {\rm{\omega }}a}\\{{v_{B\max }} = {\rm{\omega }}.2a}\end{array}} \right.\).
Áp dụng giản đồ vecto quay:
Ta có \({\rm{\alpha }} = {\mathop{\rm arcos}\nolimits} \frac{{{\rm{a\omega }}}}{{2a{\rm{\omega }}}} = \frac{{\rm{\pi }}}{3}\).
Thời gian trong 1 chu kì mà tốc độ dao động của phần tử B không lớn hơn vận tớc cực đại của phần tử M là: \(\Delta {\rm{t}} = \frac{{\rm{T}}}{{2{\rm{\pi }}}}.4\left( {\frac{{\rm{\pi }}}{2} - \alpha } \right) = \frac{{\rm{T}}}{{2{\rm{\pi }}}}.4.\left( {\frac{{\rm{\pi }}}{2} - \frac{{\rm{\pi }}}{3}} \right) = \frac{{\rm{T}}}{3} = 0,2\;{\rm{s}} \Rightarrow {\rm{T}} = 0,6\;{\rm{s}}\).
Tốc độ truyền sóng trên dây là: \({\rm{v}} = \frac{{\rm{\lambda }}}{{\rm{T}}} = \frac{{60}}{{0,6}} = 100\;{\rm{cm}}/{\rm{s}} = 1\;{\rm{m}}/{\rm{s}}\). Chọn A.
Câu 131:
 Xem đáp án
Xem đáp án
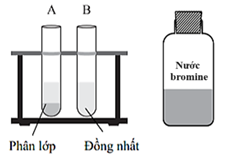
Hydrocarbon không no có khả năng tham gia phản ứng với nước bromine nên sẽ tạo thành dung dịch đồng nhất. Chọn B.
Câu 132:
Khi nung nóng, \({\rm{Ca}}{{\rm{C}}_2}{{\rm{O}}_4} \cdot {{\rm{H}}_2}{\rm{O}}\) sẽ bắt đầu mất dần khối lượng. Đồ thị hình bên biểu diễn sự phụ thuộc của khối lượng chất rắn vào nhiệt độ.
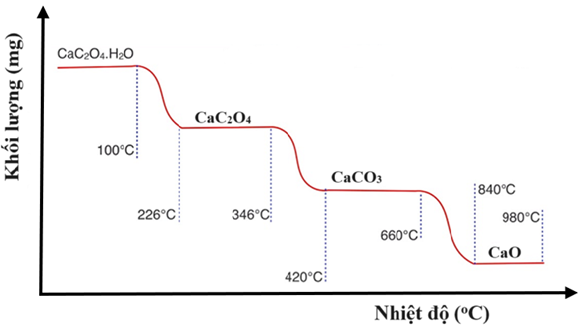
Phần trăm khối lượng chất rắn còn lại so với ban đầu tại nhiệt độ \({840^o}{\rm{C}}\) là
 Xem đáp án
Xem đáp án
Chọn số mol của \(Ca{C_2}{O_4}.1{H_2}O = 1\,mol\)→ \({m_{Ca{C_2}{O_4} \cdot {H_2}O}} = 146\,gam\)
Các phản ứng khi nung:
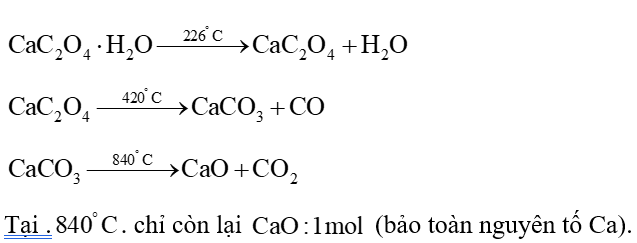
Phần trăm khối lượng chất rắn còn lại so với ban đầu là: \(\% {m_{CaO}} = \frac{{1 \cdot 56}}{{146}}.100\% \approx 38,36\% .\)
Chọn B.
Câu 133:
Trộn cùng thể tích khí chlorine và một oxide của chlorine (X) thu được 60 mL hỗn hợp khí. Tiến hành đun nóng rồi làm nguội trở lại nhiệt độ ban đầu thì thấy thể tích hỗn hợp khí thu được tăng lên 75 mL. Tiếp tục xử lý hỗn hợp với dung dịch xút dư thì thể tích giảm xuống còn 15 mL. Giả sử rằng tất cả các phép đo được thực hiện ở cùng điều kiện nhiệt độ và áp suất. Biết rằng oxide X khi đun nóng phân hủy định lượng thành oxygen và chlorine đơn chất.
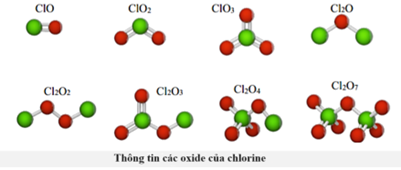
Công thức đơn giản nhất của chlorine oxide X là
 Xem đáp án
Xem đáp án
\({n_{C{l_2}}} = {n_{C{l_x}{O_y}}} = 30\) (Coi thể tích bằng với số mol trong cùng điều kiện nhiệt độ, áp suất).
Oxide \({\rm{X}}\) khi đun nóng phân hủy định lượng thành oxygen và chlorine đơn chất.
\(\begin{array}{l}2{\rm{C}}{{\rm{l}}_x}{{\rm{O}}_y} \to x{\rm{C}}{{\rm{l}}_2} + y{{\rm{O}}_2}\\30\quad \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,15x\quad \,\,\,15y\end{array}\)
\(30 + 15(x + y) = 75 \Rightarrow x + y = 3\)
Tiếp tục xử lý hỗn hợp với dung dịch xút dư thì \({\rm{C}}{{\rm{l}}_2}\) tham gia phản ứng, \({{\rm{O}}_2}\) không tham gia phản ứng nên lượng còn lại là \({{\rm{O}}_2}.\)
\({n_{{O_2}}} = 15{\rm{y}} = 15 \Rightarrow {\rm{y}} = 1,{\rm{x}} = 2\) Þ Công thức là \({\rm{C}}{{\rm{l}}_2}{\rm{O}}.\) Chọn B.
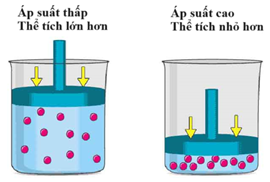
Câu 134:
Đưa 1 mol khí nitrogen vào trong ống pít-tông, thể tích pít-tông là \({V_1}\) và áp suất của hệ là 1 atm. Tiến hành tăng áp suất của hệ lên 3 atm thì thể tích của pít-tông lúc này là \({V_2}.\)
Mối liên hệ giữa \({V_1}\) và \({V_2}\) là
 Xem đáp án
Xem đáp án
Cách 1: Ta có công thức: \(PV = nRT\)trong đó P: áp suất, V: thể tích, n: số mol, T: nhiệt độ, \(R = 0,082.\)
Ban đầu: \(1\;{{\rm{V}}_1} = 1{\rm{RT}} \Rightarrow {{\rm{V}}_1} = {\rm{RT}}\)
Tăng áp suất hệ lên 3 lần: \(3\;{{\rm{V}}_2} = {\rm{RT}} \Rightarrow {{\rm{V}}_2} = \frac{{{\rm{RT}}}}{3} \Rightarrow {{\rm{V}}_1} = 3\;{{\rm{V}}_2}\)
Cách 2: Ta có: \(PV = nRT \Rightarrow V = \frac{{nRT}}{P}\)
Thể tích tỉ lệ nghịch với áp suất, khi tăng áp suất thì thể tích giảm.
Þ Tăng áp suất lên 3 lần thì thể tích giảm đi 3 lần Þ \({V_2} = \frac{{{V_1}}}{3}\)
\( \Rightarrow {{\rm{V}}_1} = 3\;{{\rm{V}}_2}.\) Chọn A.
Câu 135:
Tiến hành thí nghiệm sau: Lấy ba ống nghiệm sạch, thêm vào mỗi ống 2 mL nước cất, sau đó cho vào mỗi ống vài giọt aniline, lắc kĩ.
- Ống nghiệm thứ nhất: Để nguyên.
- Ống nghiệm thứ hai: Nhỏ từng giọt dung dịch HCl đặc, lắc nhẹ.
- Ống nghiệm thứ ba: Nhỏ từng giọt dung dịch nước bromine, lắc nhẹ.
Cho các phát biểu sau:
(a) Ở ống nghiệm thứ nhất, aniline hầu như không tan và nổi trên nước.
(b) Ở ống nghiệm thứ hai, thu được dung dịch đồng nhất.
(c) Ở ống nghiệm thứ ba, nước bromine mất màu và có kết tủa trắng.
(d) Phản ứng ở ống nghiệm thứ hai chứng tỏ aniline có tính base.
(e) Ở ống nghiệm thứ ba, nếu thay aniline bằng phenol thì thu được hiện tượng tương tự.
Số phát biểu đúng là
 Xem đáp án
Xem đáp án
Các phát biểu đúng là (b), (c), (d), (e).
Phát biểu (a) sai vì aniline nặng hơn nước sẽ chìm xuống dưới. Chọn C.
Câu 136:
 Xem đáp án
Xem đáp án
A. Tơ visco: polymer bán tổng hợp.
B. Poly(vinyl chloride): polymer tổng hợp.
C. Polyethylene: polymer tổng hợp.
D. Cellulose: polymer thiên nhiên.
Chọn A.
Câu 137:
 Xem đáp án
Xem đáp án
Phản ứng điện phân:
Đốt cháy anode:
Ta có: \({n_X} = \frac{{2,479}}{{24,79}} = 0,1\,(mol);\,{n_{C{O_2}}} = {n_{CaC{O_3}\, \downarrow }} = \frac{{0,7}}{{100}} = 0,007\,(mol)\)
Xét 2,479 lít
Trong 2,479 lít X: \({{\rm{n}}_{\rm{O}}} = 2{{\rm{n}}_{{{\rm{O}}_2}}} + 2{{\rm{n}}_{{\rm{C}}{{\rm{O}}_2}}} + {{\rm{n}}_{{\rm{CO}}}} = 0,197\;{\rm{mol}},{{\rm{n}}_{\rm{C}}} = {{\rm{n}}_{{\rm{C}}{{\rm{O}}_2}}} + {{\rm{n}}_{{\rm{CO}}}} = 0,01\;{\rm{mol}}.\)
\({{\rm{n}}_{\rm{e}}} = 2{{\rm{n}}_{\rm{O}}} = 0,394\;{\rm{mol}} \to {{\rm{m}}_{{\rm{Al}}}} = 27 \cdot \frac{{{{\rm{n}}_{\rm{e}}}}}{3} = 3,546{\rm{ gam}}{\rm{. }}\)
Trong 24 giờ: \({{\rm{m}}_{{\rm{Al}}}} = 3,546 \cdot \frac{{24 \cdot 3600}}{{0,2}}:1000 = 1532\;{\rm{kg}}.\)Chọn D.
Câu 138:
 Xem đáp án
Xem đáp án
Muối acid là muối có chứa nguyên tử hydrogen trong gốc acid, khi tan trong nước phân li ra ion H+ như \({\rm{NaHC}}{{\rm{O}}_3},Na{{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4},\,KHS, \ldots \)
Þ \(C{H_3}COONa\)là muối trung hòa. Chọn D.
Câu 139:
Sulfur dioxide phản ứng với oxygen như sau:
Khẳng định nào sau đây đúng?
(i) Tăng áp suất làm tăng hiệu suất tạo thành \({\rm{S}}{{\rm{O}}_3}.\)
(ii) Tăng nhiệt độ làm giảm hiệu suất tạo thành \({\rm{S}}{{\rm{O}}_3}.\)
(iii) Sự có mặt của xúc tác vanadium(V) oxide làm tăng hiệu suất tạo thành \({\rm{S}}{{\rm{O}}_3}.\)
 Xem đáp án
Xem đáp án
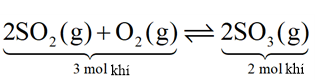
- Tăng áp suất làm tăng hiệu suất tạo thành \({\rm{S}}{{\rm{O}}_3}\) do tăng áp suất làm cân bằng chuyển dịch theo chiều giảm số mol khí, tức chiều thuận Þ (i) đúng.
- Phản ứng thuận là phản ứng tỏa nhiệt, để tăng hiệu suất tạo thành \({\rm{S}}{{\rm{O}}_3}\) cần giảm nhiệt độ của hệ Þ Tăng nhiệt độ làm giảm hiệu suất tạo thành \({\rm{S}}{{\rm{O}}_3} \Rightarrow \) (ii) đúng.
- Chất xúc tác chỉ làm tăng tốc độ phản ứng, không làm tăng hiệu suất phản ứng Þ (iii) sai.
Chọn C.
Câu 140:
 Xem đáp án
Xem đáp án
Vi khuẩn có khả năng cố định nitơ là vi khuẩn lam (Cyanobacteria). Chọn B.
Câu 141:
 Xem đáp án
Xem đáp án
Nồng độ auxin cao kích thích ra rễ, nồng độ xitôkinin cao kích thích ra chồi → Để kích thích mô sẹo (callus) mọc chồi khi nuôi cấy trong ống nghiệm, môi trường nuôi cấy cần có các hoocmôn và nồng độ tương quan như sau: nồng độ auxin thấp hơn xitôkinin (kích thích ra chồi). Chọn B.
Câu 142:
 Xem đáp án
Xem đáp án
Trong 2 loài cây này, cây lá lốt thoát nước qua cutin nhiều hơn do lá lốt là cây ưa bóng, tầng cutin mỏng. Chọn D.
Câu 143:
 Xem đáp án
Xem đáp án
A, B, D. Sai. Các sự kiện gồm: một số phân tử lactôzơ liên kết với prôtêin ức chế; ARN pôlimeraza liên kết với vùng khởi động của opêron Lac và tiến hành phiên mã; các gen cấu trúc Z, Y, A phiên mã tạo ra các phân tử mARN tương ứng đều chỉ xảy ra khi môi trường có lactôzơ.
C. Đúng. Gen điều hoà R tổng hợp prôtêin ức chế là sự kiện xảy ra trong cả điều kiện môi trường có hoặc không có lactôzơ. Chọn C.
Câu 144:
 Xem đáp án
Xem đáp án
Quá trình ngẫu phối có xu hướng làm cho quần thể đạt trạng thái cân bằng di truyền nên không làm thay đổi tỉ lệ kiểu gen. Chọn D.
Câu 145:
 Xem đáp án
Xem đáp án
Phương pháp nhân giống bằng cấy truyền phôi tạo ra các cá thể có kiểu gen giống nhau, cùng giới tính. Do có cùng giới tính nên chúng không thể giao phối với nhau để tạo ra thế hệ con; do có cùng kiểu gen nên chúng có mức phản ứng giống nhau. Tuy nhiên, những cá thể này vẫn có thể có kiểu hình khác nhau khi được nuôi trong những điều kiện môi trường khác nhau, vì kiểu hình là kết quả của sự tương tác giữa kiểu gen và môi trường. Chọn B.
Câu 146:
 Xem đáp án
Xem đáp án
Câu 147:
 Xem đáp án
Xem đáp án
Câu 148:
Ở một loài thực vật, alen A quy định thân cao trội hoàn toàn so với alen a quy định thân thấp. Cây thân cao tự thụ phấn, đời con F1 thu được 75% cây thân cao : 25% cây thân thấp. Ở F1, do cây thân thấp năng suất không cao nên người ta loại bỏ các cây thân thấp và cho các cây thân cao giao phấn tự do. Theo lí thuyết, F2 thu được tỉ lệ kiểu hình là
 Xem đáp án
Xem đáp án
F1 phân li 3 thân cao : 1 thân thấp → P dị hợp: Aa × Aa → F1: 1 AA : 2 Aa : 1 aa.
Nếu loại bỏ các cây thân thấp (aa), các cá thể F1 tham gia sinh sản là: 1 AA : 2 Aa.
Cho các cây thân cao F1 giao phấn tự do: (1 AA : 2 Aa) × (1 AA : 2 Aa) ↔ (2 A : 1 a) × (2 A : 1 a) → F2: 4 AA : 4 Aa : 1 aa (8 thân cao : 1 thân thấp). Chọn C.
Câu 149:
Ở người, bệnh bạch tạng do gen lặn a nằm trên NST thường quy định, bệnh máu khó đông do gen lặn b nằm trên NST giới tính X quy định. Xét một cặp vợ chồng, bên phía người vợ có em trai bị máu khó đông, mẹ bị bạch tạng. Bên phía người chồng có chị gái bị máu khó đông và bị bạch tạng. Những người khác trong gia đình đều không bị hai bệnh này. Cặp vợ chồng này dự định sinh 2 đứa con, xác suất cả 2 đứa con này đều mang alen bệnh về cả 2 bệnh nói trên là bao nhiêu?
Đáp án: ……….
 Xem đáp án
Xem đáp án
Xét quan hệ huyết thống, xác định kiểu gen của vợ chồng:
- Bên phía người vợ:
+ Mẹ bị bệnh bạch tạng nên vợ có kiểu gen Aa.
+ Em trai bị bệnh máu khó đông (XbY) → Kiểu gen của bố mẹ người vợ về tính trạng bệnh máu khó đông: XBXb × XBY → Kiểu gen của người vợ: \(\frac{1}{2}{X^{\rm{B}}}{X^{\rm{B}}}:\frac{1}{2}{X^{\rm{B}}}{{\rm{X}}^{\rm{b}}}\).
- Bên phía người chồng:
+ Chị gái bị bệnh bạch tạng → Kiểu gen của bố mẹ người chồng về tính trạng bệnh bạch tạng là: Aa × Aa → Kiểu gen của người chồng: \(\frac{1}{3}{\rm{AA}}:\frac{2}{3}{\rm{Aa}}\).
+ Người chồng không bị bệnh máu khó đông nên kiểu gen của chồng sẽ là \({X^B}Y\)
Xét xác suất sinh 2 đứa con mang alen gây bệnh bạch tạng là:
TH1: \(\left( {\frac{1}{3}{\rm{AA}} \times {\rm{Aa}}} \right) \Rightarrow \)Xác suất sinh 2 đứa mang alen gây bệnh bạch tạng là \(\frac{1}{3} \times {\left( {\frac{1}{2}} \right)^2} = \frac{1}{{12}}.\)
TH2: \(\left( {\frac{2}{3}{\rm{Aa}} \times {\rm{Aa}}} \right) \Rightarrow \)Xác suất sinh 2 đứa mang alen gây bệnh bạch tạng là \(\frac{2}{3} \times {\left( {\frac{3}{4}} \right)^2} = \frac{3}{8}.\)
→ Xác suất sinh 2 đứa con mang alen gây bệnh bạch tạng là: \(\frac{1}{{12}} + \frac{3}{8} = \frac{{11}}{{24}}.\)
Xét xác suất sinh 2 đứa con mang alen gây bệnh máu khó đông: \(\frac{1}{2}{X^B}{X^b} \times {X^B}Y = \frac{1}{2} \times {\left( {\frac{1}{2}} \right)^2} = \frac{1}{8}\)
Vậy xác suất cặp vợ chồng trên sinh 2 đứa con đều mang alen gây bệnh về cả hai bệnh trên sẽ là:\(\frac{{11}}{{24}} \times \frac{1}{8} = \frac{{11}}{{192}} \approx 0,057.\) Đáp án: 0,057 .