Phương trình logarit và một số phương pháp giải
-
1364 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giá trị của x thỏa mãn \[lo{g_{\frac{1}{2}}}(3 - x) = 2\;\] là
 Xem đáp án
Xem đáp án
Phương trình tương đương với:
\[3 - x = {\left( {\frac{1}{2}} \right)^2} \Leftrightarrow x = \frac{{11}}{4}\]
Vậy\[x = \frac{{11}}{4}\]
Đáp án cần chọn là: D
Câu 2:
Tập nghiệm của phương trình \[{\log _2}\left( {{x^2} - 1} \right) = {\log _2}2x\] là:
 Xem đáp án
Xem đáp án
Điều kiện:\(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 1 > 0}\\{2x > 0}\end{array}} \right. \Leftrightarrow x > 1\)
Với điều kiện này thì phương trình đã cho tương đương với
\[{x^2} - 1 = 2x \Leftrightarrow {x^2} - 2x - 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 + \sqrt 2 \left( {TM} \right)}\\{x = 1 - \sqrt 2 \left( L \right)}\end{array}} \right.\]
Vậy tập nghiệm của phương trình đã cho là \[S = \left\{ {1 + \sqrt 2 } \right\}\]
Đáp án cần chọn là: D
Câu 3:
Tìm tập nghiệm S của phương trình \[{\log _2}\left( {x - 1} \right) + {\log _2}\left( {x + 1} \right) = 3\].
 Xem đáp án
Xem đáp án
Điều kiện : x>1.
\[{\log _2}\left( {x - 1} \right) + {\log _2}\left( {x + 1} \right) = 3 \Leftrightarrow {\log _2}\left( {\left( {x - 1} \right).\left( {x + 1} \right)} \right) = 3\]
\[ \Leftrightarrow {x^2} - 1 = {2^3} \Leftrightarrow x = \pm 3\]
So sánh với điều kiện suy ra x=3.
Đáp án cần chọn là: C
Câu 4:
Tìm tập nghiệm S của phương trình \[lo{g_2}({x^2} - 4x + 3) = lo{g_2}(4x - 4)\]
 Xem đáp án
Xem đáp án
Điều kiện:\(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 4x + 3 > 0}\\{4x - 4 > 0}\end{array}} \right. \Leftrightarrow x > 3.\)
\[lo{g_2}({x^2} - 4x + 3) = lo{g_2}(4x - 4) \Leftrightarrow {x^2} - 4x + 3 = 4x - 4\]
\(\left[ {\begin{array}{*{20}{c}}{x = 1(l)}\\{x = 7}\end{array}} \right.\)
Vậy\[S = \left\{ 7 \right\}\]
Đáp án cần chọn là: B
Câu 5:
Tập hợp nghiệm của phương trình \[{\log _3}\left( {{9^{50}} + 6{x^2}} \right) = {\log _{\sqrt 3 }}\left( {{3^{50}} + 2x} \right)\] là:
 Xem đáp án
Xem đáp án
Điều kiện:\[x > - \frac{{{3^{50}}}}{2}\]
Phương trình đã cho tương đương với:
\[lo{g_3}({9^{50}} + 6{x^2}) = lo{g_3}({9^{50}} + 4x{.3^{50}} + 4{x^2})\]
\[ \Leftrightarrow 6{x^2} = 4x{.3^{50}} + 4{x^2} \Leftrightarrow {x^2} = 2x{.3^{50}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = {{2.3}^{50}}}\end{array}} \right.\]
Đáp án cần chọn là: B
Câu 6:
Hỏi có bao nhiêu giá trị m nguyên trong đoạn \[\left[ { - 2017;2017} \right]\;\]để phương trình \[logmx = 2log(x + 1)\;\;\] có nghiệm duy nhất?
 Xem đáp án
Xem đáp án
ĐK: \[x > - 1;mx > 0\]
\[\begin{array}{*{20}{l}}{\log (m{\rm{x}}) = 2\log (x + 1) \Leftrightarrow m{\rm{x}} = {{(x + 1)}^2} \Leftrightarrow {x^2} + (2 - m)x + 1 = 0}\\{{\rm{\Delta }} = {m^2} - 4m + 4 - 4 = {m^2} - 4m}\end{array}\]
Để phương trình đã cho có nghiệm duy nhất thì có 2 TH:
TH1: Phương trình trên có nghiệm duy nhất: \[{m^2} = 4m \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 0}\\{m = 4}\end{array}} \right.\]Tuy nhiên giá trị m=0 loại do khi đó nghiệm là x=−1.
TH2: Phương trình trên có 2 nghiệm thỏa: \[{x_1} \le - 1 < {x_2}\]
Nếu có \[{x_1} = - 1 \to 1 - (2 - m) + 1 = 0 \to m = 0\] thay lại vô lý
\[{x_1} < - 1 < {x_2} \to ({x_1} + 1)({x_2} + 1) < 0 \Leftrightarrow {x_1}{x_2} + {x_1} + {x_2} + 1 < 0 \to 1 + m - 2 + 1 < 0 \Leftrightarrow m < 0.\]
Như vậy sẽ có các giá trị \[ - 2017; - 2016; \ldots \ldots - 1\] và 4.
Có 2018 giá trị.
Đáp án cần chọn là: C
Câu 7:
Gọi \[{x_1},{x_2}\] là các nghiệm của phương trình \[{\left( {{{\log }_{\frac{1}{3}}}x} \right)^2} - \left( {\sqrt 3 + 1} \right){\log _3}x + \sqrt 3 = 0\]. Khi đó tích \[{x_1},{x_2}\] bằng:
 Xem đáp án
Xem đáp án
\[{\left( {{{\log }_{\frac{1}{3}}}x} \right)^2} - \left( {\sqrt 3 + 1} \right){\log _3}x + \sqrt 3 = 0\]điều kiện của phương trình là x>0
\[ \Leftrightarrow {\left( {{{\log }_3}x} \right)^2} - \left( {\sqrt 3 + 1} \right){\log _3}x + \sqrt 3 = 0\]
Đặt \[t = {\log _3}x\] phương trình trở thành:
\[{t^2} - (\sqrt 3 + 1)t + \sqrt 3 = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}}{t = 1}\\{t = \sqrt 3 }\end{array}} \right.\]
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{lo{g_3}x = 1}\\{lo{g_3}x = \sqrt 3 }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 3}\\{x = {3^{\sqrt 3 }}}\end{array}} \right. \Rightarrow {x_1}.{x_2} = {3.3^{\sqrt 3 }} = {3^{\sqrt 3 + 1}}\)
Đáp án cần chọn là: A
Câu 8:
Giả sử m là số thực sao cho phương trình \[log_3^2x - (m + 2)lo{g_3}x + 3m - 2 = 0\] có hai nghiệm \[{x_1};{x_2}\] phân biệt thỏa mãn \[{x_1}.{x_2} = 9\].
Khi đó m thỏa mãn tính chất nào sau đây?
 Xem đáp án
Xem đáp án
Đặt \[t = {\log _3}x\] suy ra phương trình trở thành\[{t^2} - (m + 2)t + 3m - 2 = 0\left( * \right)\]
Để phương trình có hai nghiệm \[{x_1};{x_2}\] thì (*) cũng có hai nghiệm \[{t_1};{t_2}\] .
Phương trình (*) có 2 nghiệm phân biệt \[{t_1};{t_2}\]
\[ \Leftrightarrow \Delta > 0 \Leftrightarrow {(m + 2)^2} - 4(3m - 2) > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m > 6}\\{m < 2}\end{array}} \right.\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{{x_1} = {3^{{t_1}}}}\\{{x_2} = {3^{{t_2}}}}\end{array}} \right. \Rightarrow {x_1}.{x_2} = {3^{{t_1} + {t_2}}} = 9 \Leftrightarrow {t_1} + {t_2} = 2.\)
Theo hệ thức Vi-ét ta có: \[{t_1} + {t_2} = m + 2\]
\[ \Rightarrow m + 2 = 2 \Leftrightarrow m = 0\]Suy ra \[m \in \left( { - 1;1} \right)\]
Đáp án cần chọn là: C
Câu 9:
Giải phương trình \[{\log _2}\left( {{2^x} - 1} \right).{\log _4}\left( {{2^{x + 1}} - 2} \right) = 1\] Ta có nghiệm:
 Xem đáp án
Xem đáp án
Phương trình đã cho tương đương với:
\[\begin{array}{l}lo{g_2}({2^x} - 1)[lo{g_4}2 + lo{g_4}({2^x} - 1)] = 1\\ \Leftrightarrow lo{g_2}({2^x} - 1)\left[ {\frac{1}{2} + \frac{1}{2}lo{g_2}({2^x} - 1)} \right] = 1\\ \Leftrightarrow lo{g_2}({2^x} - 1)\left[ {1 + lo{g_2}({2^x} - 1)} \right] = 2\\ \Leftrightarrow \log _2^2({2^x} - 1) + lo{g_2}({2^x} - 1) - 2 = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{lo{g_2}({2^x} - 1) = 1}\\{lo{g_2}({2^x} - 1) = - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{2^x} - 1 = 1}\\{{2^x} - 1 = \frac{1}{4}}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{2^x} = 3}\\{{2^x} = \frac{5}{4}}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = lo{g_2}3}\\{x = lo{g_2}\frac{5}{4}}\end{array}} \right.\end{array}\]
Đáp án cần chọn là: C
Câu 10:
Cho hai số thực dương a và b thỏa mãn \[lo{g_4}a = lo{g_6}b = lo{g_9}\left( {a + b} \right).\] Tính tỉ số \(\frac{a}{b}\).
 Xem đáp án
Xem đáp án
Đặt
\[lo{g_4}a = lo{g_6}b = lo{g_9}(a + b) = x \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = {4^x}}\\{b = {6^x}}\\{a + b = {9^x}}\end{array}} \right.\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{a}{b} = {{\left( {\frac{4}{6}} \right)}^x} = {{\left( {\frac{2}{3}} \right)}^x} > 0}\\{{4^x} + {6^x} = {9^x}\,\,\left( 1 \right)}\end{array}} \right.\)
\[\begin{array}{l}{4^x} + {6^x} = {9^x} \Leftrightarrow {\left( {\frac{2}{3}} \right)^{2x}} + {\left( {\frac{2}{3}} \right)^x} - 1 = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{{\left( {\frac{2}{3}} \right)}^{2x}} = \frac{{ - 1 + \sqrt 5 }}{2}}\\{{{\left( {\frac{2}{3}} \right)}^{2x}} = \frac{{ - 1 - \sqrt 5 }}{2} < 0\left( {loai} \right)}\end{array}} \right. \Rightarrow \frac{a}{b} = \frac{{ - 1 + \sqrt 5 }}{2}\end{array}\]
Đáp án cần chọn là: A
Câu 11:
Phương trình \[{\log _4}\left( {{{3.2}^x} - 1} \right) = x - 1\] có hai nghiệm là \[{x_1};{x_2}\;\] thì tổng \[{x_1} + {x_2}\;\] là:
 Xem đáp án
Xem đáp án
\[{\log _4}\left( {{{3.2}^x} - 1} \right) = x - 1 \Leftrightarrow {3.2^x} - 1 = {4^{x - 1}} \Leftrightarrow {4^x} - {12.2^x} + 4 = 0\]
Đặt \[t = {2^x}\] khi đó phương trình trở thành \[{t^2} - 12t + 4 = 0\] phương trình có hai nghiệm\[{t_1},{t_2}\] thỏa mãn\[{t_1}{t_2} = 4 \Leftrightarrow {2^{{x_1}}}{.2^{{x_2}}} = 4 \Leftrightarrow {2^{{x_1} + {x_2}}} = {2^2} \Leftrightarrow {x_1} + {x_2} = 2\]
Đáp án cần chọn là: C
Câu 12:
Cho phương trình \[{\log _3}x.{\log _5}x = {\log _3}x + {\log _5}x\]. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Điều kiện x>0
Ta đặt\[{\log _3}x = u;{\log _5}x = v \Rightarrow u.v = u + v\]
Khi đó\[x = {3^u} = {5^v}\] suy ra\[{\log _3}{3^u} = {\log _3}{5^v} \Leftrightarrow u = v{\log _3}5\]
\[ \Rightarrow uv = u + v \Leftrightarrow {v^2}{\log _3}5 = v{\log _3}5 + v \Leftrightarrow {v^2}{\log _3}5 - v\left( {{{\log }_3}5 + 1} \right) = 0\]
\[ \Leftrightarrow v\left( {v{{\log }_3}5 - {{\log }_3}5 - 1} \right) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{v = 0}\\{vlo{g_3}5 - lo{g_3}5 - 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{v = 0}\\{v = \frac{{lo{g_3}5 + 1}}{{lo{g_3}5}}}\end{array}} \right. = 1 + \frac{1}{{lo{g_3}5}}\)
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{u = 0}\\{u = 1 + lo{g_3}5}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1(TM)}\\{x = {3^{1 + lo{g_3}5}} = 15(TM)}\end{array}} \right.\)
Do đó phương trình có hai nghiệm \[{x_1} = 1,{x_2} = 15\] và tổng hai nghiệm bằng 16 là một số chính phương.
Đáp án cần chọn là: D
Câu 13:
Tìm tất cả các giá trị thực của m để phương trình \[2lo{g_2}|x| + lo{g_2}|x + 3| = m\;\] có 3 nghiệm thực phân biệt.
 Xem đáp án
Xem đáp án
TXĐ : D=R.
\[2{\log _2}\left| x \right| + {\log _2}\left| {x + 3} \right| = m \Leftrightarrow {\log _2}{\left| x \right|^2} + {\log _2}\left| {x + 3} \right| = m\]
\[ \Leftrightarrow {\log _2}\left( {{{\left| x \right|}^2}.\left| {x + 3} \right|} \right) = m \Leftrightarrow {\left| x \right|^2}.\left| {x + 3} \right| = {2^m}\]
\[ \Leftrightarrow {x^2}.\left| {x + 3} \right| = {2^m}\]
Xét hàm\[f(x) = {x^2}.\left| {x + 3} \right|\]Ta có : \[f(x) = {x^2}.\left| {x + 3} \right| = \left| {{x^3} + 3{x^2}} \right|\]
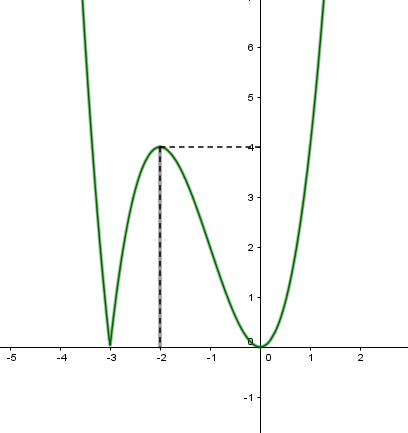
Để phương trình có 3 nghiệm phân biệt thì \[{2^m} = 4 \Leftrightarrow m = 2\]
Đáp án cần chọn là: D
Câu 14:
Cho a, b, x là các số thực dương khác 1 thỏa: \[4\log _a^2x + 3\log _b^2x = 8{\log _a}x.{\log _b}x\quad (1)\] Mệnh đề (1) tương đương với mệnh đề nào sau đây:
 Xem đáp án
Xem đáp án
\[4\log _a^2x - 8{\log _b}x.{\log _a}x + 3\log _b^2x = 0\]
Ta có:
\[\;\Delta \prime = {(4lo{g_b}x)^2} - 3.4.lo{g_b}x = 4log_b^2x > 0\]
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{lo{g_a}x = \frac{3}{2}lo{g_b}x}\\{lo{g_a}x = \frac{1}{2}lo{g_b}x}\end{array}} \right.\)
Suy ra
\[{\log _a}x = \frac{3}{2}{\log _b}x \Rightarrow {\log _a}x = {\log _{\sqrt[3]{{{b^2}}}}}x \Rightarrow a = \sqrt[3]{{{b^2}}} \Rightarrow {a^3} = {b^2}\]
\[{\log _a}x = \frac{1}{2}{\log _b}x \Rightarrow {\log _a}x = {\log _{{b^2}}}x \Rightarrow a = {b^2}\]
Đáp án cần chọn là: B
Câu 15:
Cho x>0; \[x \ne 1\] thỏa mãn biểu thức \[\frac{1}{{lo{g_2}x}} + \frac{1}{{lo{g_3}x}} + ... + \frac{1}{{lo{g_{2017}}x}} = M\;\]. Khi đó x bằng:
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{VT = {{\log }_x}2 + {{\log }_x}3 + {{\log }_x}4 + ... + {{\log }_x}2017 = {{\log }_x}(2.3.4...2017)}\\{ \Rightarrow {x^M} = 2017! \Rightarrow x = \sqrt[M]{{2017!}}}\end{array}\]
Đáp án cần chọn là: D
Câu 16:
Tìm tập nghiệm của phương trình \[{\log _3}x + \frac{1}{{{{\log }_9}x}} = 3\]
 Xem đáp án
Xem đáp án
Điều kiện:\[x > 0;x \ne 1\]
\[{\log _3}x + \frac{1}{{{{\log }_9}x}} = 3 \Leftrightarrow {\log _3}x + \frac{2}{{{{\log }_3}x}} = 3 \Leftrightarrow {\left( {{{\log }_3}x} \right)^2} - 3{\log _3}x + 2 = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{lo{g_3}x = 1}\\{lo{g_3}x = 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 3}\\{x = {3^2} = 9}\end{array}} \right.\)
Đáp án cần chọn là: D
Câu 17:
Tìm tập hợp tất cả các giá trị của tham số m để phương trình \[lo{g_2}x - lo{g_2}(x - 2) = m\] có nghiệm
 Xem đáp án
Xem đáp án
Phương trình đã cho tương đương với\(\left\{ {\begin{array}{*{20}{c}}{lo{g_2}\left( {\frac{x}{{x - 2}}} \right) = m}\\{x > 2}\end{array}} \right.\)
Để phương trình đã cho có nghiệm thì đường thẳng y=m cắt đồ thị hàm số\[y = {\log _2}f\left( x \right)\] với \[f\left( x \right) = \frac{x}{{x - 2}}\] trên khoảng\[\left( {2; + \infty } \right)\]
Có\[f'\left( x \right) = - \frac{2}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x > 2\] và\[\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\] nên ta có các tập giá trị của các hàm số là \[f\left( x \right) \in \left( {1; + \infty } \right) \Rightarrow {\log _2}f\left( x \right) \in \left( {0; + \infty } \right)\]</>
Vậy\[0 < m < + \infty \]Đáp án cần chọn là: D
Câu 18:
Số nghiệm của phương trình \[{\log _3}\left| {{x^2} - \sqrt 2 x} \right| = {\log _5}\left( {{x^2} - \sqrt 2 x + 2} \right)\] là
 Xem đáp án
Xem đáp án
Đặt \[{x^2} - \sqrt 2 x = t\] khi đó\[{\log _3}|t| = {\log _5}(t + 2)(t > - 2;t \ne 0)\]
Đặt\[\;lo{g_3}|t| = lo{g_5}(t + 2) = a \Rightarrow \left\{ {\begin{array}{*{20}{c}}{|t| = {3^a}}\\{t + 2 = {5^a}}\end{array}} \right.\]
\[ \Rightarrow |{5^a} - 2| = {3^a} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{5^a} - 2 = - {3^a}}\\{{5^a} - 2 = {3^a}}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{{5^a} + {3^a} = 2\left( 1 \right)}\\{{5^a} = {3^a} + 2\left( 2 \right)}\end{array}} \right.\]
Xét (1):\[f(a) = {5^a} + {3^a} \Rightarrow f'(a) = {5^a}\ln 5 + {3^a}\ln 3 > 0(\forall a \in R)\] nên hàm số đồng biến trên R
Mặt khác\[f(0) = 2\] do đó phương trình\[f(a) = f(0)\] có 1 nghiệm duy nhất\[a = 0 \Rightarrow t = - 1\]
Suy ra: \[{x^2} - \sqrt 2 x + 1 = 0\] (vô nghiệm)
Xét (2) \[ \Leftrightarrow {\left( {\frac{3}{5}} \right)^a} + 2.{\left( {\frac{1}{5}} \right)^a} = 1\]
Đặt
\[g(a) = {\left( {\frac{3}{5}} \right)^a} + 2.{\left( {\frac{1}{5}} \right)^a} \Rightarrow g'(a) = {\left( {\frac{3}{5}} \right)^a}\ln \frac{3}{5} + 2.{\left( {\frac{1}{5}} \right)^a}\ln \frac{1}{5} < 0(\forall a \in R)\]
Nên hàm số g(a) nghịch biến trên R do đó phương trình g(a)=1 có tối đa 1 nghiệm.
Mà g(a)=g(1) nên a=1
Suy ra \[t = 3 \Rightarrow {x^2} - \sqrt 2 x - 3 = 0\] có 2 nghiệm phân biệt thỏa mãn điều kiện
Vậy phương trình đã cho có 2 nghiệm.
Đáp án cần chọn là: B
Câu 19:
Hỏi phương trình \[2{\log _3}\left( {\cot x} \right) = {\log _2}\left( {\cos x} \right)\]có bao nhiêu nghiệm trong khoảng \[\left( {0;2017\pi } \right).\]
 Xem đáp án
Xem đáp án
Điều kiện : \(\left\{ {\begin{array}{*{20}{c}}{cotx > 0}\\{cosx > 0}\end{array}} \right.\left( 1 \right)\)
Ta có :\[2{\log _3}\left( {\cot x} \right) = {\log _2}\left( {\cos x} \right) \Leftrightarrow {\log _3}{\left( {\cot x} \right)^2} = {\log _2}\left( {\cos x} \right) = t\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{{(cotx)}^2} = {3^t}}\\{co{s^2}x = {4^t}}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{co{s^2}x}}{{si{n^2}x}} = {3^t}}\\{co{s^2}x = {4^t}}\end{array}} \right.\)
\[ \Rightarrow \frac{{{4^t}}}{{1 - {4^t}}} = {3^t} \Leftrightarrow {4^t} - {3^t} + {12^t} = 0 \Leftrightarrow {\left( {\frac{4}{3}} \right)^t} + {4^t} = 1\]
Đặt \[f(t) = {\left( {\frac{4}{3}} \right)^t} + {\left( 4 \right)^t} \Rightarrow f'(t) = {\left( {\frac{4}{3}} \right)^t}\ln \frac{4}{3} + {\left( 4 \right)^t}\ln 4 > 0\]suy ra\[f(t) = 1\]có tối đa 1 nghiệm.
Nhận thấy t=−1 là nghiệm của phương trình
\[ \Rightarrow {\log _2}\left( {\cos x} \right) = - 1 \Rightarrow \cos x = \frac{1}{2} \Rightarrow x = \pm \frac{\pi }{3} + k2\pi \Rightarrow x = \frac{\pi }{3} + k2\pi \]( do đk (1)).
Ta có : \[0 < \frac{\pi }{3} + k2\pi < 2017\pi \Leftrightarrow - \frac{1}{6} < k < \frac{{3025}}{3}\]Do k nguyên nên\[k = 0,1, \ldots ,1008\]
Vậy phương trình có 1009 nghiệm.
Đáp án cần chọn là: A
Câu 20:
Phương trình sau đây có bao nhiêu nghiệm\[\left( {{x^2} - 4} \right)\left( {{{\log }_2}x + {{\log }_3}x + {{\log }_4}x + ... + {{\log }_{19}}x - \log _{20}^2x} \right) = 0\]
 Xem đáp án
Xem đáp án
\[({x^2} - 4)({\log _2}x + {\log _3}x + {\log _4}x + ... + {\log _{19}}x - \log _{20}^2x) = 0( * )\]
Đkxđ: x>0
\(\left( * \right) \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 2(tm)}\\{x = - 2(ktm)}\\{{{\log }_2}x + {{\log }_3}x + {{\log }_4}x + ... + {{\log }_{19}}x - \log _{20}^2x = 0\left( {**} \right)}\end{array}} \right.\)
\[( * * ) \Leftrightarrow \frac{{logx}}{{log2}} + \frac{{logx}}{{log3}} + \frac{{logx}}{{log4}} + ... + \frac{{logx}}{{log19}} - {\left( {\frac{{logx}}{{log20}}} \right)^2}\]
\[( * * ) \Leftrightarrow \frac{{logx}}{{log2}} + \frac{{logx}}{{log3}} + \frac{{logx}}{{log4}} + ... + \frac{{logx}}{{log19}} - {\left( {\frac{{logx}}{{log20}}} \right)^2}\]
\[ \Leftrightarrow logx\left( {\frac{1}{{log2}} + \frac{1}{{log3}} + \frac{1}{{log4}} + ... + \frac{1}{{log19}} - \frac{{logx}}{{lo{g^2}20}}} \right)\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{logx = 0}\\{\frac{1}{{log2}} + \frac{1}{{log3}} + \frac{1}{{log4}} + ... + \frac{1}{{log19}} - \frac{{logx}}{{lo{g^2}20}} = 0}\end{array}} \right.\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{\frac{1}{{log2}} + \frac{1}{{log3}} + \frac{1}{{log4}} + ... + \frac{1}{{log19}} = \frac{{logx}}{{lo{g^2}20}}}\end{array}} \right.\]
\[\begin{array}{l} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{\left( {\frac{1}{{log2}} + \frac{1}{{log3}} + \frac{1}{{log4}} + ... + \frac{1}{{log19}}} \right)lo{g^2}20 = \log x}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1\left( {tm} \right)}\\{x = {{10}^{\left( {\frac{1}{{log2}} + \frac{1}{{log3}} + \frac{1}{{log4}} + ... + \frac{1}{{log19}}} \right)lo{g^2}20}}\left( {tm} \right)}\end{array}} \right.\end{array}\]
Phương trình (*) có 3 nghiệm.
Đáp án cần chọn là: C
Câu 21:
Tìm m để phương trình \[mln(1 - x) - lnx = m\] có nghiệm \[x \in \left( {0;1} \right)\]
 Xem đáp án
Xem đáp án
+ Cô lập\[m:m(\ln (1 - x) - 1) = \ln x \Rightarrow m = \frac{{\ln x}}{{\ln (1 - x) - 1}}\] với 1>x>0 .
+ Nhận xét đáp án: ta thấy \[\frac{{\ln x}}{{\ln (1 - x) - 1}} > 0,\forall 0 < x < 1\] Loại C và D
+ Tính giới hạn của\[y = \frac{{\ln x}}{{\ln (1 - x) - 1}}\] khi x tiến dần tới 1 thì thấy y dần tiến tới 0 . Loại B.
Đáp án cần chọn là: A
Câu 22:
Tổng tất cả các nghiệm của phương trình \[{\log _3}\left( {7 - {3^x}} \right) = 2 - x\] bằng:
 Xem đáp án
Xem đáp án
\[{\log _3}\left( {7 - {3^x}} \right) = 2 - x\]
Điều kiện:\[7 - {3^x} > 0\]
\[pt \Leftrightarrow 7 - {3^x} = {3^{2 - x}} \Leftrightarrow 7 - {3^x} = \frac{9}{{{3^x}}} \Leftrightarrow {7.3^x} - {\left( {{3^x}} \right)^2} = 9\, \Leftrightarrow {3^{2x}} - {7.3^x} + 9 = 0\,\,\left( * \right)\]
Đặt \[t = {3^x}\;\;\left( {t > 0} \right) \Rightarrow x = {\log _3}t\] Thay vào phương trình (*) ta có:\[ \Leftrightarrow {t^2} - 7t + 9 = 0\,\,\,\,\left( { * * } \right)\]
Nhận thấy (**) có: \[{\rm{\Delta }} = 13 > 0,\;\;S = 7 > 0,\;\;P = 9 > 0 \Rightarrow \] phương trình (**) có 2 nghiệm dương phân biệt giả sử là: \[{t_1};{t_2}\]
Áp dụng hệ thức Vi-et cho phương trình (**) ta được:\(\left\{ {\begin{array}{*{20}{c}}{{t_1} + {t_2} = 7}\\{{t_1}{t_2} = 9}\end{array}} \right.\)
Khi đó ta có: \[{x_1} + {x_2} = {\log _3}{t_1} + {\log _3}{t_2} = {\log _3}\left( {{t_1}{t_2}} \right) = {\log _3}9 = 2\]
Đáp án cần chọn là: A
Câu 23:
Cho \[0 \le x \le 2020\]và \[lo{g_2}(2x + 2) + x - 3y = {8^y}\]. Có bao nhiêu cặp số (x;y) nguyên thỏa mãn các điều kiện trên?
 Xem đáp án
Xem đáp án
Ta có:
\[{\log _2}\left( {2x + 2} \right) + x - 3y = {8^y} \Leftrightarrow {\log _2}\left( {x + 1} \right) + x + 1 = {2^{3y}} + 3y\left( * \right)\]
Xét hàm số \[y = f\left( x \right) = {2^x} + x\] có\[f'\left( x \right) = {2^x}\ln 2 + 1 > 0\,\,\forall x \in \mathbb{R}\]=> Hàm số đồng biến trên \(\mathbb{R}\)
⇒ Phương trình (*)\[ \Leftrightarrow f\left( {{{\log }_2}\left( {x + 1} \right)} \right) = f\left( {3y} \right) \Leftrightarrow {\log _2}\left( {x + 1} \right) = 3y\]
Do \[0 \le x \le 2020\] nên \[0 \le {\log _2}\left( {x + 1} \right) \le {\log _2}2021 \Rightarrow 0 \le 3y \le {\log _2}2021\]
\[ \Leftrightarrow 0 \le y \le \frac{{{{\log }_2}2021}}{3} \Rightarrow y \in \left\{ {0;1;2;3} \right\}\]Với mỗi giá trị y vừa tìm được đều tìm được đúng 1 giá trị x nguyên thỏa mãn
⇒Có 4 cặp số (x;y) nguyên thỏa mãn các điều kiện trên.
Đáp án cần chọn là: D
Câu 24:
Có bao nhiêu số nguyên \[a \in \left( { - 2019;2019} \right)\] để phương trình \[\frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} = x + a\] có hai nghiệm phân biệt?
 Xem đáp án
Xem đáp án
\[\frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} = x + a \Leftrightarrow f\left( x \right) = \frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} - x = a\,\,\left( * \right)\]
Xét hàm số\[f\left( x \right) = \frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} - x\]
ĐKXĐ:\(\left\{ {\begin{array}{*{20}{c}}{x + 5 > 0}\\{\begin{array}{*{20}{c}}{ln(x + 5) \ne 0}\\{{3^x} - 1 \ne 0}\end{array}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > - 5}\\{x + 5 \ne 1}\\{{3^x} \ne 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > - 5}\\{x \ne - 4}\\{x \ne 0}\end{array}} \right.\)
\[ \Rightarrow D = \left( { - 5; - 4} \right) \cup \left( { - 4;0} \right) \cup \left( {0; + \infty } \right)\]
Ta có:
\[f'\left( x \right) = - \frac{1}{{\left( {x + 5} \right){{\ln }^2}\left( {x + 5} \right)}} - \frac{{{3^x}\ln 3}}{{{{\left( {{3^x} - 1} \right)}^2}}} - 1 < 0,\forall x \in D\]
BBT:
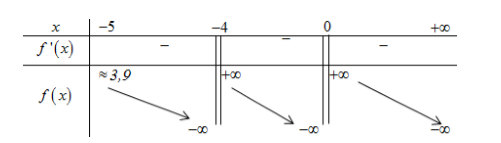
Từ BBT suy ra phương trình (*) có 2 nghiệm \[ \Leftrightarrow a \ge 4\]
Kết hợp ĐK \[ \Rightarrow a \in \left\{ {4;...;2018} \right\}\]Vậy có 2015 giá trị của a thỏa mãn.
Đáp án cần chọn là: D
Câu 25:
Cho x,y là các số thực dương thỏa mãn \[lo{g_2}\frac{{3x + 3y + 4}}{{{x^2} + {y^2}}} = (x + y - 1)(2x + 2y - 1) - 4\left( {xy + 1} \right)\] Giá trị lớn nhất của biểu thức \[P = \frac{{5x + 3y - 2}}{{2x + y + 1}}\;\] bằng:
 Xem đáp án
Xem đáp án
\[lo{g_2}\frac{{3x + 3y + 4}}{{{x^2} + {y^2}}} = (x + y - 1)(2x + 2y - 1) - 4\left( {xy + 1} \right)\]
\[ \Leftrightarrow lo{g_2}(3x + 3y + 4) - lo{g_2}({x^2} + {y^2}) = (x + y - 1)[2(x + y) - 1] - 4(xy + 1)\]
\[ \Leftrightarrow lo{g_2}(3x + 3y + 4) - lo{g_2}({x^2} + {y^2}) = 2{(x + y)^2} - 3(x + y) + 1 - 4(xy + 1)\]
\[ \Leftrightarrow lo{g_2}(3x + 3y + 4) - lo{g_2}({x^2} + {y^2}) = 2({x^2} + {y^2}) + 4xy - (3x + 3y) + 1 - 4xy - 4\]
\[ \Leftrightarrow lo{g_2}(3x + 3y + 4) - lo{g_2}({x^2} + {y^2}) = 2({x^2} + {y^2}) - (3x + 3y + 4) + 1\]
\[ \Leftrightarrow lo{g_2}(3x + 3y + 4) + (3x + 3y + 4) = lo{g_2}({x^2} + {y^2}) + 2({x^2} + {y^2}) + lo{g_2}2\]
\[ \Leftrightarrow lo{g_2}(3x + 3y + 4) + (3x + 3y + 4) = lo{g_2}(2{x^2} + 2{y^2}) + (2{x^2} + 2{y^2})( * )\]
Xét hàm số đặc trưng \[f\left( t \right) = {\log _2}t + t\,\,\left( {t > 0} \right)\] ta có
\[f'\left( t \right) = \frac{1}{{t\ln 2}} + 1 > 0\,\,\forall t > 0\]
⇒ Hàm số y=f(t) luôn đồng biến trên\[\left( {0; + \infty } \right)\]
Do đó \[\left( * \right) \Leftrightarrow 3x + 3y + 4 = 2{x^2} + 2{y^2}\]Ta có:\[{\left( {x + y} \right)^2} \le 2\left( {{x^2} + {y^2}} \right) = 3x + 3y + 4\]
\[ \Leftrightarrow {\left( {x + y} \right)^2} - 3\left( {x + y} \right) - 4 \le 0 \Leftrightarrow - 1 \le x + y \le 4\]
Kết hợp điều kiện đề bài ta có\[0 < x + y \le 4\]
Xét biểu thức
\[P = \frac{{5x + 3y - 2}}{{2x + y + 1}} = \frac{{2\left( {2x + y + 1} \right) + x + y - 4}}{{2x + y + 1}} = 2 + \frac{{x + y - 4}}{{2x + y + 1}}\]
Do \[x + y \le 4 \Leftrightarrow x + y - 4 \le 0 \Leftrightarrow \frac{{x + y - 4}}{{2x + y + 1}} \le 0 \Rightarrow P \le 2\]
Vậy\[{P_{max}} = 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + y = 4}\\{x = y}\end{array}} \right. \Leftrightarrow x = y = 2\]
Đáp án cần chọn là: C
Câu 26:
Cho hàm số \[f\left( x \right) = {\log _2}\left( {\cos x} \right).\] Phương trình \[f\prime \left( x \right) = 0\;\] có bao nhiêu nghiệm trong khoảng \[\left( {0;2020\pi } \right)?\]
 Xem đáp án
Xem đáp án
ĐKXĐ: \[\cos x > 0\]
Ta có: \[f\left( x \right) = {\log _2}\left( {\cos x} \right) \Rightarrow f'\left( x \right) = \frac{{ - \sin x}}{{\cos x.\ln 2}}\]
\[f'\left( x \right) = 0 \Leftrightarrow \frac{{ - \sin x}}{{\cos x.\ln 2}} = 0 \Leftrightarrow \tan x = 0 \Leftrightarrow x = k\pi ,\,k \in \mathbb{Z}\]
Với k chẵn, đặt\[k = 2m\,\,\left( {m \in \mathbb{Z}} \right)\]khi đó ta có\[x = m2\pi \,\,\left( {m \in \mathbb{Z}} \right)\]
Với k lẻ, đặt\[k = 2n + 1\,\,\left( {n \in \mathbb{Z}} \right)\]khi đó ta có\[x = \left( {2n + 1} \right)\pi = \pi + n2\pi \,\,\left( {n \in \mathbb{Z}} \right)\]
Kiểm tra ĐKXĐ:
\[x = m2\pi \Rightarrow \cos x = 1 > 0\]thỏa mãn.
\[x = \pi + k2\pi \Rightarrow \cos x = - 1 < 0\] loại.
Suy ra nghiệm của phương trình là\[x = m2\pi ,\,\,m \in \mathbb{Z}\]
Theo bài ra ta có: \[x \in \left( {0;2020\pi } \right) \Rightarrow 0 < m2\pi < 2020\pi \Leftrightarrow 0 < m < 1010 \Rightarrow \]Có 1009 giá trị nguyên của m thỏa mãn.
Vậy phương trình \[f'\left( x \right) = 0\]có 1009 nghiệm trong khoảng\[\left( {0;2020\pi } \right)\]
Đáp án cần chọn là: B
Câu 27:
Cho a,b,c là các số thực dương khác 1 thỏa mãn \[\log _a^2b + \log _b^2c = {\log _a}\frac{c}{b} - 2{\log _b}\frac{c}{b} - 3\]. Gọi \[M,m\;\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \[P = lo{g_a}b - lo{g_b}c\]. Giá trị của biểu thức \[S = m - 3M\;\] bằng
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{*{20}{l}}{\,\,\,\,\,\,\,\log _a^2b + \log _b^2c = {{\log }_a}\frac{c}{b} - 2{{\log }_b}\frac{c}{b} - 3}\\{ \Leftrightarrow \log _a^2b + \log _b^2c = {{\log }_a}c - {{\log }_a}b - 2{{\log }_b}c - 1}\\{ \Leftrightarrow \log _a^2b + \log _b^2c = {{\log }_b}c.{{\log }_a}b - {{\log }_a}b - 2{{\log }_b}c - 1\,\,\left( * \right)}\end{array}\]
Đặt\[{\log _a}b = x \Rightarrow {\log _b}c = x - P\]
Phương trình \[\left( * \right) \Leftrightarrow {x^2} + {\left( {x - P} \right)^2} = \left( {x - P} \right)x - x - 2\left( {x - P} \right) - 1\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow 2{x^2} - 2Px + {P^2} = {x^2} - Px - 3x + 2P - 1}\\{ \Leftrightarrow {x^2} - \left( {P - 3} \right)x + {P^2} - 2P + 1 = 0\,\,\,\left( { * * } \right)}\end{array}\]
Ta có:\[{\rm{\Delta }} = {\left( {P - 3} \right)^2} - 4\left( {{P^2} - 2P + 1} \right) = - 3{P^2} + 2P + 5\]
Phương trình (**) có nghiệm
\[ \Leftrightarrow \Delta \ge 0 \Leftrightarrow - 3{P^2} + 2P + 5 \ge 0 \Leftrightarrow - 1 \le P \le \frac{5}{3}\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{m = - 1}\\{M = \frac{5}{3}}\end{array}} \right.\)
Vậy\[S = m - 3M = - 1 - 3.\frac{5}{3} = - 6\]
Đáp án cần chọn là: C
Câu 28:
Cho các số thực a,b,c thuộc khoảng \[\left( {1; + \infty } \right)\;\]và thỏa mãn \[\,\,\,\,\,\,\log _{\sqrt a }^2b + {\log _b}c.{\log _b}\left( {\frac{{{c^2}}}{b}} \right) + 9{\log _a}c = 4{\log _a}b\]. Giá trị của biểu thức \[lo{g_a}b + lo{g_b}{c^2}\;\] bằng:
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{*{20}{l}}{\,\,\,\,\,\,\log _{\sqrt a }^2b + {{\log }_b}c.{{\log }_b}\left( {\frac{{{c^2}}}{b}} \right) + 9{{\log }_a}c = 4{{\log }_a}b}\\{ \Leftrightarrow 4\log _a^2b + {{\log }_b}c.\left( {2{{\log }_b}c - 1} \right) + 9{{\log }_a}c = 4{{\log }_a}b}\\{ \Leftrightarrow 4\log _a^2b + 2\log _b^2c - {{\log }_b}c + 9{{\log }_a}b.{{\log }_b}c = 4{{\log }_a}b\,\,\left( * \right)}\end{array}\]
Đặt \[x = {\log _a}b,\,\,y = {\log _b}c\] ta có:\(\left\{ {\begin{array}{*{20}{c}}{x = lo{g_a}b > lo{g_a}1 = 0}\\{y = lo{g_b}c > lo{g_b}1 = 0}\end{array}} \right.(do\,\,\,a,b,c > 1)\)
Khi đó phương trình (*) trở thành:
\[4{x^2} + 2{y^2} - y + 9xy = 4x\]
\[ \Leftrightarrow 4{x^2} + xy + 8xy + 2{y^2} - y - 4x = 0\]
\[ \Leftrightarrow x(4x + y) + 2y(4x + y) - (4x + y) = 0\]
\[ \Leftrightarrow (4x + y)(x + 2y - 1) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x + y = 0}\\{x + 2y - 1 = 0}\end{array}} \right.\)
TH1:\[y = - 4x\] loại do x,y>0.
TH2: \[x + 2y - 1 = 0 \Leftrightarrow x + 2y = 1\] khi đó ta có:\[{\log _a}b + {\log _b}{c^2} = x + 2y = 1\]Đáp án cần chọn là: A
Câu 29:
Cho phương trình: \[{4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\frac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\] với m là tham số. Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là:
 Xem đáp án
Xem đáp án
Ta có:
\[{4^{ - \left| {x - m} \right|}}.{\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}}.{\log _{\frac{1}{2}}}\left( {2\left| {x - m} \right| + 2} \right) = 0\]
\[ \Leftrightarrow {2^{ - 2|x - m|}}.2.lo{g_2}({x^2} - 2x + 3) - {2^{2x - {x^2}}}.lo{g_2}(2|x - m| + 2) = 0\]
\[ \Leftrightarrow {2^{ - 2|x - m| + 1}}.lo{g_2}({x^2} - 2x + 3) = {2^{2x - {x^2}}}.lo{g_2}(2|x - m| + 2)\]
\[ \Leftrightarrow {2^{{x^2} - 2x}}.lo{g_2}({x^2} - 2x + 3) = {2^{2|x - m| - 1}}.lo{g_2}(2|x - m| + 2)\]
\[ \Leftrightarrow {2^{{x^2} - 2x}} + 2.lo{g_2}({x^2} - 2x + 3) = {2^{2|x - m| + 2}}.lo{g_2}(2|x - m| + 2)\]
Xét hàm đặc trưng\[f\left( t \right) = {2^t}.{\log _2}t\,\,\left( {t \ge 2} \right)\] ta có
\[f'\left( t \right) = {2^t}.\ln 2.{\log _2}t + {2^t}.\frac{1}{{t\ln 2}} > 0\,\,\forall t \ge 2\] do đó hàm số đồng biến trên\[\left[ {2; + \infty } \right)\]
Lại có\[f\left( {{x^2} - 2x + 3} \right) = f\left( {2\left| {x - m} \right| + 2} \right)\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow {x^2} - 2x + 3 = 2\left| {x - m} \right| + 2}\\{ \Leftrightarrow {x^2} - 2x + 1 = 2\left| {x - m} \right|}\\{ \Leftrightarrow {{\left( {x - 1} \right)}^2} = 2\left| {x - m} \right|\,\,\left( * \right)}\end{array}\]
Để phương trình ban đầu có 3 nghiệm phân biệt thì phương trình (*) phải có 3 nghiệm phân biệt.
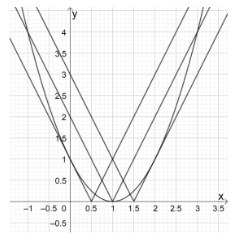
Dựa vào đồ thị hàm số ta có \[m = \frac{1}{2},\,\,m = 1,\,\,m = \frac{3}{2}\] thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: D
Câu 30:
Cho các số thực dương a,b,c khác 1 thỏa mãn
Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \[P = lo{g_a}ab - lo{g_b}bc\]. Tính giá trị của biểu thức \[S = 2{m^2} + 9{M^2}\].
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{l}\log _a^2b + \log _b^2c + 2{\log _b}\frac{c}{b} = {\log _a}\frac{c}{{{a^3}b}}\\ \Leftrightarrow \log _a^2b + \log _b^2c + 2{\log _b}c - 2 = {\log _a}c - {\log _a}\left( {{a^3}b} \right)\\ \Leftrightarrow \log _a^2b + \log _b^2c + 2{\log _b}c - 2 = {\log _a}c - 3 - {\log _a}b\\ \Leftrightarrow \log _a^2b + \log _b^2c = {\log _a}b.{\log _b}c - 2{\log _b}c - {\log _a}b - 1\left( 1 \right)\end{array}\]
Đặt \[x = {\log _a}b,\,\,y = {\log _b}c\] khi đó ta có:
\[\begin{array}{*{20}{l}}{P = {{\log }_a}ab - {{\log }_b}bc}\\{P = 1 + {{\log }_a}b - 1 - {{\log }_b}c}\\{P = x - y \Rightarrow y = x - P}\end{array}\]Thay x,y vào (1) ta có:
\[\begin{array}{*{20}{l}}{{x^2} + {y^2} = xy - 2y - x - 1}\\{ \Leftrightarrow {x^2} + {{\left( {x - P} \right)}^2} = x\left( {x - P} \right) - 2\left( {x - P} \right) - x - 1}\\{ \Leftrightarrow {x^2} + {x^2} - 2Px + {P^2} = {x^2} - Px - 2x + 2P - x - 1}\\{ \Leftrightarrow {x^2} - \left( {P - 3} \right)x + {P^2} - 2P + 1 = 0\,\,\left( 2 \right)}\end{array}\]
Để tồn tại các số a,b,c thỏa mãn yêu cầu bài toán thì phương trình (2) phải có nghiệm.
\[\begin{array}{*{20}{l}}{ \Rightarrow {\rm{\Delta }} \ge 0}\\{ \Leftrightarrow {{\left( {P - 3} \right)}^2} - 4\left( {{P^2} - 2P + 1} \right) \ge 0}\\{ \Leftrightarrow {P^2} - 6P + 9 - 4{P^2} + 8P - 4 \ge 0}\\{ \Leftrightarrow - 3{P^2} + 2P + 5 \ge 0}\\{ \Leftrightarrow - 1 \le P \le \frac{5}{3}}\end{array}\]
Vậy\[m = - 1,\,\,M = \frac{5}{3} \Rightarrow S = 2{m^2} + 9{M^2} = 2.{\left( { - 1} \right)^2} + 9.{\left( {\frac{5}{3}} \right)^2} = 27\]
Đáp án cần chọn là: D
