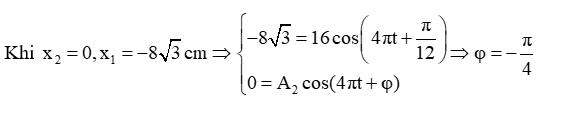Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
473 lượt thi
-
165 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Một nhóm đàn ông và phụ nữ được hỏi là họ lái loại phương tiện nào, ô tô con hay xe tải. Dữ liệu này đã được chèn vào bảng tần suất hai chiều trong hình sau:
|
|
Ô tô con |
Xe tải |
Tổng |
|
Đàn ông |
21 |
38 |
60 |
|
Phụ nữ |
135 |
45 |
180 |
|
Tổng |
156 |
84 |
240 |
Dựa trên biểu đồ, nếu 300 phụ nữ được hỏi họ lái xe hơi hay xe tải, chúng ta có thể đoán được bao nhiêu người sē nói rằng họ lái xe hơi?
 Xem đáp án
Xem đáp án
Câu 2:
Trong không gian \[Oxyz,\] cho ba điểm \[A\left( {3\,;\,\,5\,;\, - 1} \right),\,\,B\left( {7\,;\,\,x\,;\,\,1} \right)\] và \(C\left( {9\,;\,\,2\,;\,\,y} \right).\) Để ba điểm \[A,\,\,B,\,\,C\] thẳng hàng thì giá trị \(x + y\) bằng
 Xem đáp án
Xem đáp án
Ta có \(\overrightarrow {AB} = \left( {4\,;\,\,x - 5\,;\,\,2} \right),\,\,\overrightarrow {AC} = \left( {6\,;\,\, - 3\,;\,\,y + 1} \right).\)
Ba điểm A, B, C thẳng hàng \( \Leftrightarrow \exists k \in \mathbb{R}:\overrightarrow {AB} = k \cdot \overrightarrow {AC} \)
\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4 = 6k}\\{x - 5 = - 3k}\\{2 = k\left( {y + 1} \right)}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{k = \frac{2}{3}}\\{x = 3\,;\,\,y = 2}\end{array}{\rm{.}}} \right.} \right.\] Vậy \(x + y = 5\). Chọn A.
Câu 3:
Cho hai số phức \({z_1} = 1 + i\) và \({z_2} = 2 + i.\) Trên mặt phẳng \[Oxy,\] điểm biểu diễn số phức \({z_1} + 2{z_2}\) có tọa độ là
 Xem đáp án
Xem đáp án
Ta có \({z_1} + 2{z_2} = \left( {1 + i} \right) + 2\left( {2 + i} \right) = 5 + 3i.\)
Suy ra điểm biểu diễn số phức \({z_1} + 2{z_2}\) có toạ độ là \[\left( {5\,;\,\,3} \right).\] Chọn D.
Câu 4:
Tính đạo hàm của hàm số $y={{\cos }^{2}}\left( 2x+1 \right).$
 Xem đáp án
Xem đáp án
Ta có \(y = {\cos ^2}\left( {2x + 1} \right).\)
Suy ra \(y' = 2\cos \left( {2x + 1} \right) \cdot {\left[ {\cos \left( {2x + 1} \right)} \right]^\prime }\)\( \Rightarrow y' = 2\cos \left( {2x + 1} \right) \cdot 2\left[ { - \sin \left( {2x + 1} \right)} \right]\)
\[ \Rightarrow y' = - 4\cos \left( {2x + 1} \right) \cdot \sin \left( {2x + 1} \right) = - 2\sin \left( {4x + 2} \right).\] Chọn D.
Câu 5:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh $a$, cạnh bên \[SA\] vuông góc với đáy và $SA=a\sqrt{3}.$ Khoảng cách từ điểm $A$ đến mặt phẳng $\left( SBC \right)$ bằng
 Xem đáp án
Xem đáp án
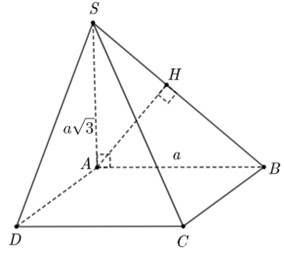
Kẻ $AH\bot SB\,\,(*)$
Ta có $BC\bot AB$ (do ABCD là hình vuông); $BC\bot SA$(do $SA\bot \left( ABCD \right)$.
Suy ra $BC\bot \left( SAB \right)\Rightarrow BC\bot AH\,\,(**)$
Từ $(*),(**)$ suy ra $AH\bot (SBC).$ Suy ra $d\left( A,\left( SBC \right) \right)=AH$.Xét tam giác vuông \[SAB,\] có $\frac{1}{A{{H}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{S{{A}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{3{{a}^{2}}}=\frac{4}{3{{a}^{2}}}\Rightarrow AH=\frac{a\sqrt{3}}{2}.$
Chọn D.
Câu 6:
Trong không gian Oxyz cho A(2;1;1) và đường thẳng Gọi là đường thẳng đi qua A vuông góc với đường thẳng d và cắt trục hoành. Một vectơ chỉ phương của đường thẳng là
 Xem đáp án
Xem đáp án
Gọi \[B=\Delta \cap Ox\Rightarrow B\left( x\,;\,\,0\,;\,\,0 \right)\Rightarrow \overrightarrow{AB}=\left( x-2\,;\,-1\,;\,-1 \right).\]
Do $\Delta \bot d$ nên $1\cdot \left( x-2 \right)+2\cdot \left( -1 \right)+3\cdot \left( -1 \right)=0\Rightarrow x=7\Rightarrow \overrightarrow{AB}=\left( 5\,;\,\,-1\,;\,\,-1 \right).$
Khi đó đường thẳng $\Delta $ nhận một vectơ chỉ phương là $\vec{u}=\overrightarrow{AB}=\left( 5\,;\,\,-1\,;\,\,-1 \right).$ Chọn B.
Câu 7:
 Xem đáp án
Xem đáp án
Ta có phương trình hoành độ giao điểm: \(\frac{{{x^2} - 2x + 3}}{{x - 1}} = 3x - 6\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x - 1 \ne 0}\\{{x^2} - 2x + 3 = \left( {x - 1} \right)\left( {3x - 6} \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{{x^2} - 2x + 3 = 3{x^2} - 9x + 6}\end{array}} \right.} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne 1}\\{2{x^2} - 7x + 3 = 0}\end{array}} \right.\,\,\,(*)\)
Hệ phương trình \((*)\) có hai nghiệm phân biệt nên số giao điểm của của đồ thị hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) và đường thẳng \(y = 3x - 6\) là 2. Chọn D.
Câu 8:
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác vuông tại \(A\,,\,\,AC = a\,,\,\,\widehat {ACB} = 60^\circ .\) Đường thẳng \(BC'\) tạo với \(\left( {ACC'A'} \right)\) một góc \(30^\circ .\) Tính thể tích \(V\) của khối trụ \(ABC.A'B'C'\).
 Xem đáp án
Xem đáp án
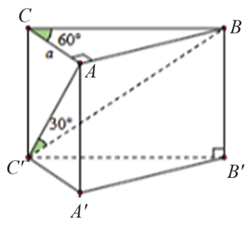
Xét tam giác \[ABC\] vuông tại \(A\) ta có:
\(\tan 60^\circ = \frac{{AB}}{{AC}} \Rightarrow AB = a\sqrt 3 .\)
Khi đó \({S_{ABC}} = \frac{1}{2}AB \cdot AC = \frac{{{a^2}\sqrt 3 }}{2}.\)
Ta có hình chiếu vuông góc của cạnh \(BC'\) trên mặt phẳng \(\left( {ACC'A'} \right)\) là \(AC'\) \( \Rightarrow \widehat {BC'A} = 30^\circ {\rm{. }}\)
Xét tam giác \(AB{C^\prime }\) vuông tại \(A\) ta có: \[\tan 30^\circ = \frac{{AB}}{{AC'}} \Leftrightarrow \frac{1}{{\sqrt 3 }} = \frac{{a\sqrt 3 }}{{AC'}} \Rightarrow AC' = 3a.\]
Suy ra \(CC' = \sqrt {A{{C'}^2} - A{C^2}} = 2a\sqrt 2 .\)
Thể tích của khối trụ là \({V_{ABC.A'B'C'}} = CC' \cdot {S_{ABC}} = 2a\sqrt 2 \cdot \frac{1}{2} \cdot a \cdot a\sqrt 3 = {a^3}\sqrt 6 .\) Chọn B.
Câu 9:
Cho hàm số \(f(x) = - \frac{1}{3}{x^3} + m{x^2} + \left( {3m + 2} \right)x - 5.\) Tập hợp các giá trị của tham số \(m\) để hàm số nghịch biến trên \(\mathbb{R}\) là \[\left[ {a\,;\,b} \right].\] Khi đó giá trị của \(2a - b\) bằng
 Xem đáp án
Xem đáp án
Hàm số xác định với mọi \(x \in \mathbb{R}.\)
Ta có \(f'(x) = - {x^2} + 2mx + 3m + 2.\)
Hàm số nghịch biến trên \(\mathbb{R}\) khi \(f'(x) \le 0,\forall x \in \mathbb{R}\)
\( \Leftrightarrow \Delta ' \le 0 \Leftrightarrow {m^2} + 3m + 2 \le 0 \Leftrightarrow - 2 \le m \le - 1\).
Hay \(m \in \left[ { - 2;\, - 1} \right] \Rightarrow a = - 2,\,\,b = - 1 \Rightarrow 2a - b = - 3.\) Chọn B.
Câu 10:
Trong không gian \[Oxyz,\] cho mặt phẳng \(\left( P \right):2x + y - z + 5 = 0\) và hai điểm \(A\left( {0\,;\,\,0\,;\,\,4} \right),B\left( {2\,;\,\,0\,;\,\,0} \right).\) Phương trình mặt cầu đi qua \[O,\,\,A,\,\,B\] và tiếp xúc với mặt phẳng \((P)\) là
 Xem đáp án
Xem đáp án
Gọi \((S)\) có tâm \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) và bán kính R.
Phương trình mặt cầu \((S)\) có dạng:\({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0.{\rm{ }}\)
Theo giả thiết, \((S)\) đi qua ba điểm \[O,\,\,A,\,\,B\], ta có hệ phương trình:
\[\left\{ {\begin{array}{*{20}{l}}{d = 0}\\{ - 8c + d = - 16}\\{ - 4a + d = - 4}\\{\frac{{\left| {2a + b - c + 5} \right|}}{{\sqrt {4 + 1 + 1} }} = R}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{d = 0}\\{c = 2}\\{a = 1}\\{{{\left( {2 + b - 2 + 5} \right)}^2} = 6\left( {{1^2} + {b^2} + {2^2} - 0} \right)}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 1}\\{c = 2}\\{d = 0}\end{array}.} \right.} \right.} \right.\]
Vậy \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 6.\) Chọn A.
Câu 11:
Cho phương trình \[\left( {m - 1} \right){x^2} - 2\left( {m + 2} \right)x + m + 1 = 0\], với \(m\) là tham số. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) sao cho \({x_1} + {x_2} - {x_1}{x_2}\) là một số nguyên?
 Xem đáp án
Xem đáp án
Phương trình đã cho có hai nghiệm phân biệt \({x_1},\,\,{x_2}\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{m \ne 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{\left( {m + 2} \right)}^2} - \left( {m - 1} \right)\left( {m + 1} \right) > 0}\\{m \ne 1}\end{array}} \right.} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} + 4m + 4 - {m^2} + 1 > 0}\\{m \ne 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - \frac{5}{4}}\\{m \ne 1}\end{array}.} \right.} \right.\)
Khi đó \({x_1} + {x_2} - {x_1}{x_2} = \frac{{2(m + 2)}}{{m - 1}} - \frac{{m + 1}}{{m - 1}} = 1 - \frac{4}{{m - 1}}.\)
Để \({x_1} + {x_2} - {x_1}{x_2}\) là một số nguyên \( \Rightarrow \frac{4}{{m - 1}}\) là một số nguyên.
\( \Rightarrow m - 1\) là ước của 4 mà Ư\(\left( 4 \right) = \left\{ { \pm 4\,;\,\, \pm 2\,;\,\, \pm 1} \right\}\)
\[ \Rightarrow \left[ {\begin{array}{*{20}{l}}{m - 1 = 1}\\{m - 1 = - 1}\\{m - 1 = 4}\\{m - 1 = - 4}\\{m - 1 = 2}\\{m - 1 = - 2}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{m = 2}\\{m = 0}\\{m = 4}\\{m = - 3\,\,(L)}\\{m = 3}\\{m = - 1}\end{array} \Rightarrow m \in \left\{ { - 1\,;\,\,0\,;\,\,2\,;\,\,3\,;\,\,4} \right\}} \right.} \right.\].
Vậy có 5 giá trị nguyên của \(m\) thoả mãn yêu cầu bài toán. Chọn C.
Câu 12:
Có bao nhiêu giá trị nguyên dương của \(m\) để hàm số \(y = {x^2} + 8\ln 2x - mx\) đồng biến trên \(\left( {0\,;\, + \infty } \right)?\)
 Xem đáp án
Xem đáp án
Tập xác định \(D = \left( {0\,;\,\, + \infty } \right)\). Ta có \(y' = 2x + \frac{8}{x} - m\).
Hàm số đồng biến trên \(\left( {0\,;\,\, + \infty } \right)\) khi \(y' \ge 0\,,\,\,\forall x \in \left( {0\,;\,\, + \infty } \right)\)
\( \Leftrightarrow m \le 2x + \frac{8}{x}\,,\,\,\forall x \in \left( {0\,;\,\, + \infty } \right)\).
Đặt \(f(x) = 2x + \frac{8}{x}\), có \(f'(x) = 2 - \frac{8}{{{x^2}}} = \frac{{2{x^2} - 8}}{{{x^2}}},f'(x) = 0 \Leftrightarrow x = 2\).
Bảng biến thiên
|
\(x\) |
0 |
2 |
\( + \infty \) |
|
\(f'\left( x \right)\) |
\( - \) |
0 + |
|
|
\(f\left( x \right)\) |
|
|
\( + \infty \) |
|
|
|
8 |
|
Suy ra hàm số đồng biến trên \(\left( {0\,;\,\, + \infty } \right)\) khi \(m \le 8\) hay \[m \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6\,;\,\,7\,;\,\,8} \right\}\].
Vậy có 8 giá trị của \(m\) thoả mãn yêu cầu bài toán. Chọn A.
Câu 13:
Một mảnh vườn hình đa giác có chu vi bằng 63m độ dài các cạnh là các số nguyên lập thành một cấp số nhân có công bội bằng 2. Hỏi số cạnh của đa giác đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi \({u_1},\,\,q\) lần lượt là số hạng đầu tiên và công bội của dãy số gồm các cạnh của mảnh vườn. Ta có \({u_1} \in \mathbb{Z},\,\,{u_1} > 0,\,\,q = 2\).
Vì mảnh vườn là hình đa giác nên \(n > 3\).
\({S_n} = {u_1} \cdot \frac{{{q^n} - 1}}{{q - 1}} = 63 \Leftrightarrow {u_1} \cdot \frac{{{2^n} - 1}}{{2 - 1}} = 63\)\( \Leftrightarrow {u_1} \cdot \left( {{2^n} - 1} \right) = 63 \Leftrightarrow {u_1} = \frac{{63}}{{{2^n} - 1}} \in \mathbb{Z}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{2^n} - 1 \in U(63)}\\{{2^n} - 1 > 0}\\{n > 3}\end{array}} \right.\)\[ \Rightarrow {2^n} - 1 \in \left\{ {3\,;\,\,7\,;\,\,9\,;\,\,63} \right\} \Leftrightarrow {2^n} \in \left\{ {4\,;\,\,8\,;\,\,10\,;\,\,64} \right\}\]
\( \Rightarrow n \in \left\{ {2\,;\,\,3\,;\,\,6} \right\} \Rightarrow n = 6 \Rightarrow {u_1} = 1\). Vậy đa giác đó có 6 cạnh. Chọn C.
Câu 14:
Số nghiệm nguyên x thoả mãn là
 Xem đáp án
Xem đáp án
Điều kiện xác định: \(x > 0.\)
Ta có \({\log _2}x + {\log _3}x \ge 1 + {\log _2}x \cdot {\log _3}x \Leftrightarrow \left( {{{\log }_2}x - 1} \right)\left( {{{\log }_3}x - 1} \right) \le 0\)
Suy ra có 2 nghiệm nguyên \(x\) thoả mãn. Chọn B.
Câu 15:
Cho \(\int {\left( {a{x^2} + bx + 5} \right)} \,{e^x}\;{\rm{d}}x = \left( {3{x^2} - 8x + 13} \right){e^x} + C\) với \[a\,,\,\,b\] là các số nguyên. Giá trị biểu thức \(S = a + b\) bằng
 Xem đáp án
Xem đáp án
Xét \(I = \int {\left( {a{x^2} + bx + 5} \right)\,} {e^x}\;{\rm{d}}x\). Đặt \(\left\{ {\begin{array}{*{20}{l}}{u = a{x^2} + bx + 5 \Rightarrow {\rm{d}}u = (2ax + b){\rm{d}}x}\\{\;{\rm{d}}v = {e^x}\;{\rm{d}}x \Rightarrow v = {e^x}}\end{array}} \right.\).
Khi đó: \(I = \int {\left( {a{x^2} + bx + 5} \right)} \,{e^x}\;{\rm{d}}x = \left( {a{x^2} + bx + 5} \right){e^x} - \int {(2ax + b)} \,{e^x}\;{\rm{d}}x\)
\( = \left( {a{x^2} + bx + 5} \right){e^x} - \left( {2ax + b} \right){e^x} + \int 2 a \cdot {e^x}\;{\rm{d}}x\)
\( = \left( {a{x^2} + bx + 5} \right){e^x} - \left( {2ax + b} \right){e^x} + 2a{e^x} + C\)\[ = {e^x}\left[ {a{x^2} + \left( {b - 2a} \right) + \left( {5 - b + 2a} \right)} \right] + C.\]
Ta có \(\int {\left( {a{x^2} + bx + 5} \right)\,} {e^x}\;{\rm{d}}x = \left( {3{x^2} - 8x + 13} \right){e^x} + C\)
\( \Leftrightarrow {e^x}\left[ {a{x^2} + \left( {b - 2a} \right) + \left( {5 - b + 2a} \right)} \right] + C = \left( {3{x^2} - 8x + 13} \right){e^x} + C\)
\( \Leftrightarrow a{x^2} + \left( {b - 2a} \right) + \left( {5 - b + 2a} \right) = 3{x^2} - 8x + 13\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 3}\\{b - 2a = - 8}\\{5 - b + 2a = 13}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 3}\\{b = - 2}\end{array}} \right.} \right.\) (thoả mãn)
Suy ra \(S = a + b = 1.\) Chọn A.
Câu 16:
Các giá trị thực của tham số \(m\) để hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{2m\left( {x + 1} \right) \ge x + 3}\\{4mx + 3 \ge 4x}\end{array}} \right.\) có nghiệm duy nhất là
 Xem đáp án
Xem đáp án
Ta có \(\left\{ {\begin{array}{*{20}{l}}{2m\left( {x + 1} \right) \ge x + 3}\\{4mx + 3 \ge 4x}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left( {2m - 1} \right)x \ge 3 - 2m}\\{\left( {4m - 4} \right)x \ge - 3}\end{array}} \right.} \right.\)
Giả sử hệ có nghiệm duy nhất thì \(\frac{{3 - 2m}}{{2m - 1}} = \frac{{ - 3}}{{4m - 4}}\)\( \Leftrightarrow 8{m^2} - 26m + 15 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = \frac{3}{4}}\\{m = \frac{5}{2}}\end{array}.} \right.\)
Thử lại:
• Với \(m = \frac{3}{4}\), hệ trở thành \(\left\{ {\begin{array}{*{20}{l}}{\left( {\frac{3}{2} - 1} \right)x \ge 3 - \frac{3}{2}}\\{ - x \ge - 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge 3}\\{x \le 3}\end{array} \Leftrightarrow x = 3} \right.} \right.\) (thoả mãn)
• Với \(m = \frac{5}{2}\), hệ trở thành \(\left\{ {\begin{array}{*{20}{l}}{4x \ge - 2}\\{6x \ge - 3}\end{array} \Leftrightarrow x \ge - \frac{1}{2}} \right.\) (không thoả mãn)
Vậy \(m = \frac{3}{4}\) là giá trị cần tìm. Chọn B.
Câu 17:
Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu \({v_0} = 500\;{\rm{m}}/{\rm{s}}\) hợp với phương ngang một góc \(\alpha .\) Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }} \cdot {x^2} + x \cdot \tan \alpha \), trong đó \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\) là gia tốc trọng trường. Góc bắn \(\alpha \) để quả đạn bay xa nhất là
 Xem đáp án
Xem đáp án
Ta có \(y = 0 \Leftrightarrow \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }} \cdot {x^2} + x \cdot \tan \alpha = 0\)
\( \Leftrightarrow x\left( {\frac{{ - g}}{{2v_0^2\cos \alpha }} \cdot x + \tan \alpha } \right) = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \frac{{x_0^2\sin 2\alpha }}{g} = 25\,\,000\sin 2\alpha .}\end{array}} \right.\)
Do đó, tầm bay xa mà quả đạn đạt tới là \(25\,\,000\sin 2\alpha \,\,(m).\)
Vậy đạn bay xa nhất khi \(\sin 2\alpha = 1 \Leftrightarrow 2\alpha = \frac{\pi }{2} + k2\pi \Leftrightarrow \alpha = \frac{\pi }{4} + k\pi .\)
Vì \(0 \le \alpha \le \frac{\pi }{2}\) nên \(\alpha = \frac{\pi }{4}.\)
Vậy góc bắn bằng \(45^\circ \) thì đạn bay xa nhất. Chọn B.
Câu 18:
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \({z^2} - 2mz + 6m - 5 = 0\) có hai nghiệm phức phân biệt \({z_1},\,\,{z_2}\) thoả mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right|\)?
 Xem đáp án
Xem đáp án
• TH1: \({z_1},\,\,{z_2}\) là các nghiệm thực \( \Leftrightarrow \Delta ' > 0 \Leftrightarrow {m^2} - 6m + 5 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 5}\\{m < 1}\end{array}} \right..\)
Ta có \(\left| {{z_1}} \right| = \left| {{z_2}} \right| \Leftrightarrow {z_1} = - {z_2} \Leftrightarrow {z_1} + {z_2} = 0 \Leftrightarrow 2m = 0 \Leftrightarrow m = 0.\)
• TH2: \({z_1},\,\,{z_2}\) là các nghiệm ảo \( \Leftrightarrow \Delta ' < 0 \Leftrightarrow {m^2} - 6m + 5 < 0 \Leftrightarrow 1 < m < 5.\)
Phương trình bậc hai có hai nghiệm phức phân biệt thì hai số phức đó là hai số phức liên hợp nên luôn thoả mãn điều kiện \(\left| {{z_1}} \right| = \left| {{z_2}} \right|\)
\( \Rightarrow m \in \left( {1\,;\,\,5} \right){\rm{. M\`a }}m \in \mathbb{Z} \Rightarrow m \in \left\{ {2\,;\,\,3\,;\,\,4} \right\}{\rm{. }}\)
Vậy có 4 giá trị \(m\) thoả mãn. Chọn A.
Câu 19:
 Xem đáp án
Xem đáp án
Gọi \(k\) là hệ số góc của đường thẳng \(d\) qua \[A.\]
Ta có phương trình của \(d\) có dạng: \(y = kx + m - k.\)
\(d\) tiếp xúc với \((C) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{kx + m - k = {x^3} + 3{x^2} + 1}\\{k = 3{x^2} + 6x}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m = - 2{x^3} + 6x + 1\,\,(*)}\\{k = 3{x^2} + 6x}\end{array}} \right.} \right.\) có nghiệm.
Để qua \(A\) có thể kẻ được đúng 3 tiếp tuyến tới \((C)\).
Khi phương trình (*) phải có 3 nghiệm phân biệt
\( \Leftrightarrow {y_{CT}} < m < {y_{CD}}\) với \(f(x) = - 2{x^3} + 6x + 1.\)
Ta có \[f'(x) = - 6{x^2} + 6\,;\,\,f'(x) = 0 \Leftrightarrow x = \pm 1.\] \(f(1) = 5 = {f_{CD}};\,\,f( - 1) = - 3 = {f_{CT}}.\)
Suy ra \( - 3 < m < 5.\) Vậy số phần tử của \(S\) là 7. Chọn B.
Câu 20:
Một chất điểm chuyển động trên đường thẳng \[Ox\] nằm ngang (chiều dương hướng sang phải) với gia tốc phụ thuộc thời gian \[t\] (giây) là . Biết vận tốc ban đầu bằng 10m/s. Hỏi trong 6 giây đầu tiên, thời điểm nào chất điểm ở xa nhất về phía bên phải?
 Xem đáp án
Xem đáp án
Vận tốc của vật được tính theo công thức \(v(t) = 10 + {t^2} - 7t\,\,(m/s).\)
Quãng đường vật đi được tính theo công thức \(S\left( t \right) = \int v (t)dt = \frac{{{t^3}}}{3} - \frac{7}{2}{t^2} + 10t\,\,(m).\)
Ta có \(S'\left( t \right) = {t^2} - 7t + 10 \Rightarrow S'\left( t \right) = 0 \Leftrightarrow {t^2} - 7t + 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 2}\\{t = 5}\end{array}} \right.\)
\( \Rightarrow S\left( 0 \right) = 0;\,\,S\left( 2 \right) = \frac{{26}}{3};\,\,S\left( 5 \right) = \frac{{25}}{6};\,\,S\left( 6 \right) = 6\)\( \Rightarrow {\max _{[0;\,\,6]}}S(t) = S(2) = \frac{{26}}{3}.\) Chọn D.
Câu 21:
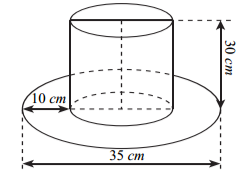
Một cái mũ bằng vải của nhà ảo thuật với kích thước như hình vẽ. Tổng diện tích vải cần có để làm nên cái mũ (không tính viền, mép, phần thừa) là
 Xem đáp án
Xem đáp án
Bán kính hình trụ của cái mũ là: \(r = \frac{{35 - 10 - 10}}{2} = \frac{{15}}{2}(\;{\rm{cm}}).\)
Đường cao hình trụ của cái mũ là \(30\,\;{\rm{cm}}.\)
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rl = 2\pi \cdot \frac{{15}}{2} \cdot 30 = 450\pi \,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Diện tích vành mũ là: \({S_v} = \pi {\left( {\frac{{35}}{2}} \right)^2} - {S_d}\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Vậy tổng diện tích vải cần có để làm nên cái mũ là:
\(S = {S_{xq}} + {S_d} + {S_v} = 450\pi + {\left( {\frac{{35}}{2}} \right)^2}\pi = 756,25\pi \,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\) Chọn B.
Câu 22:
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = {m^2}{x^4} - \left( {{m^2} - 2019m} \right){x^2} - 1\) có đúng một cực trị?
 Xem đáp án
Xem đáp án
• TH1: \(m = 0 \Rightarrow y = - 1\) nên hàm số không có cực trị \( \Rightarrow m = 0\) (loại).
• TH2: \(m \ne 0 \Rightarrow {m^2} > 0.\)
Hàm số \(y = {m^2}{x^4} - \left( {{m^2} - 2019m} \right){x^2} - 1\) có đúng một cực trị \( \Leftrightarrow ab \ge 0\)
\( \Leftrightarrow - {m^2}\left( {{m^2} - 2019m} \right) \ge 0 \Leftrightarrow {m^2} - 2019m \le 0 \Leftrightarrow 0 \le m \le 2019.{\rm{ }}\)
Vì \(m \ne 0 \Rightarrow 0 < m \le 2019.\)
Do \(m \in \mathbb{Z}\) nên có 2019 giá trị của tham số \(m\) thoả mãn yêu cầu bài toán. Chọn A.
Câu 23:
Cho hình cầu \(\left( S \right)\) tâm \(O\), bán kính bằng \[2a.\] Xét khối nón đỉnh \(O\), có đường tròn đáy nằm trên \(\left( S \right)\) và góc giữa đường sinh và mặt đáy bằng \(60^\circ .\) Thể tích của khối nón đó bằng
 Xem đáp án
Xem đáp án
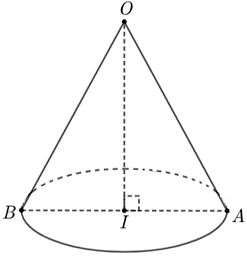
Khối nón đỉnh \(O\), có đường tròn đáy nằm trên \(\left( S \right)\) nên đường sinh của khối nón bằng bán kính của mặt cầu.
Xét khối nón như hình với \(I\) và trung điểm AB.
Vì góc giữa đường sinh và mặt đáy bằng \(60^\circ \) nên \(\widehat {OAI} = 60^\circ \)
\( \Rightarrow OI = AI \cdot \tan 60^\circ = AI\sqrt 3 \) (1)
Ta có: \(A{I^2} + O{I^2} = O{A^2} = 4{a^2}\)
Từ (1), (2) ta có \(OI = a\sqrt 3 \,,\,\,AI = a\).
Thể tích của khối nón là: \(V = \frac{1}{3}\pi A{I^2} \cdot OI = \frac{1}{3}\pi {a^2} \cdot a\sqrt 3 = \frac{{\sqrt 3 \pi {a^3}}}{3}\). Chọn B.
Câu 24:
Trong không gian \[Oxyz,\] cho 4 điểm \(A\left( {2\,;\,\,0\,;\,\,2} \right),\) \(B\left( {1\,;\,\, - 1\,;\,\, - 2} \right),C\left( { - 1\,;\,\,1\,;\,\,0} \right),\)\(D\left( { - 2\,;\,\,1\,;\,\,2} \right).\) Thể tích của khối tứ diện \[ABCD\] bằng
 Xem đáp án
Xem đáp án
Ta có \(\overrightarrow {AC} = \left( { - 3\,;\,\,1\,;\,\, - 2} \right)\,;\,\,\overrightarrow {AB} = \left( { - 1\,;\,\, - 1\,;\,\, - 4} \right)\,;\,\,\overrightarrow {AD} = \left( { - 4\,;\,\,1\,;\,\,0} \right).\)
Suy ra \(\left[ {\overrightarrow {AB} \,;\,\,\overrightarrow {AC} } \right] = \left( { - 6\,;\,\, - 10\,;\,\,4} \right).\)
Thể tích khối tứ diện \[ABCD\] là \[V = \frac{1}{6} \cdot \left| {\,\left[ {\overrightarrow {AB} \,;\,\,\overrightarrow {AC} } \right] \cdot \overrightarrow {AD} } \right| = \frac{1}{6} \cdot \left| {14} \right| = \frac{7}{3}.\] Chọn D.
Câu 25:
Trên mặt phẳng tọa độ \[Oxy,\] cho hai điểm \(A\left( {1\,;\,\,1} \right),B\left( {4\,;\,\, - 3} \right).\) Gọi \(C(a;b)\) thuộc đường thẳng \((d):x - 2y - 1 = 0\) sao cho khoảng cách từ \(C\) đến đường thẳng \(AB\) bằng 6 . Biết rằng \(C\) có hoành độ nguyên, giá trị của \(a + b\) bằng
 Xem đáp án
Xem đáp án
Ta có \(\overrightarrow {AB} = \left( {3\,;\,\, - 4} \right).\)
Suy ra, phương trình tổng quát của đường thẳng \[AB\] có dạng: \(4x + 3y + m = 0.\)
• Vì \(A\left( {1\,;\,\,1} \right) \in AB\) nên \(4.1 + 3.1 + m = 0 \Leftrightarrow m = - 7 \Rightarrow AB:4x + 3y - 7 = 0.\)
• Vì \(C\left( {a\,;\,\,b} \right) \in d:x - 2y - 1 = 0 \Rightarrow a - 2b - 1 = 0 \Rightarrow a = 2b + 1.\)
Theo giả thiết, ta có \(d\left( {C\,;\,\,AB} \right) = 6 \Leftrightarrow \frac{{\left| {4a + 3b - 7} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 6 \Leftrightarrow \left| {4a + 3b - 7} \right| = 30.\)
Thay \(a = 2b + 1\) vào phương trình trên ta được \(\left| {4\left( {2b + 1} \right) + 3b - 7} \right| = 30 \Leftrightarrow \left| {11b - 3} \right| = 30\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{11b - 3 = 30}\\{11b - 3 = - 30}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{b = 3}\\{b = \frac{{ - 27}}{{11}}}\end{array}.} \right.} \right.\) Do \(C\) có toạ độ nguyên nên \(b = 3 \Rightarrow a = 7 \Rightarrow a + b = 10.\)
Chọn A.
Câu 26:
 Xem đáp án
Xem đáp án
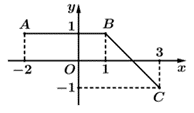
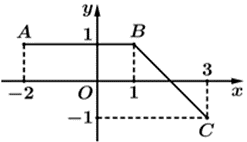 Gọi \[G,{\rm{ }}H\] lần lượt là hình chiếu của \[A,\,\,B\] trên \[Ox.\]
Gọi \[G,{\rm{ }}H\] lần lượt là hình chiếu của \[A,\,\,B\] trên \[Ox.\]
Gọi \(D\) là giao điểm của \[BC\] và \[Ox,{\rm{ }}E\] là hình chiếu của \(C\) trên \[Ox.\]
Suy ra \[ABGH\] là hình chữ nhật, \(\Delta BGD\) và \(\Delta CDE\) là tam giác vuông.
Với \(AB = 3,\,\,AD = 1,\,\,BG = 1\), \(GD = DE = 1.\)
Ta có \(\int\limits_{ - 2}^3 {f(x){\rm{d}}x} = {S_{ABGH}} + {S_{BGD}} - {S_{CDE}}\)\(T = \frac{1}{{10}}.\)
Suy ra \(\int\limits_{ - 2}^3 {f(x){\rm{d}}x} = 3 \cdot 1 + \frac{1}{2} \cdot 1 \cdot 1 - \frac{1}{2} \cdot 1 \cdot 1 = 3\). Chọn D.
Câu 27:
Cho \[a,{\rm{ }}b,{\rm{ }}c\] đều khác 0 thỏa mãn \({4^a} = {25^b} = {10^c}.\) Tính \(T = \frac{c}{a} + \frac{c}{b}.\)
 Xem đáp án
Xem đáp án
Đặt \({4^a} = {25^b} = {10^c} = t.\)
• \({4^a} = t \Leftrightarrow a = {\log _4}t\);
• \({25^b} = t \Leftrightarrow b = {\log _5}t\);
• \({10^c} = t \Leftrightarrow c = {\log _{10}}t\).
Suy ra \(T = \frac{c}{a} + \frac{c}{b} = \frac{{{{\log }_{10}}t}}{{{{\log }_4}t}} + \frac{{{{\log }_{10}}t}}{{{{\log }_{25}}t}} = \frac{{{{\log }_t}4}}{{{{\log }_t}10}} + \frac{{{{\log }_t}25}}{{{{\log }_t}10}}\)\( = \frac{{{{\log }_t}4.25}}{{{{\log }_t}10}} = \frac{{{{\log }_t}100}}{{{{\log }_t}10}} = 2.\)
Chọn C.
Câu 28:
Trong không gian \[Oxyz,\] xét mặt cầu \(\left( S \right)\) có phương trình dạng \({x^2} + {y^2} + {z^2} - 4x + 2y - 2az + 10a = 0.\) Tập hợp các giá trị thực của tham số \(a\) để \(\left( S \right)\) có chu vi đường tròn lớn nhất bằng \(8\pi \) là
 Xem đáp án
Xem đáp án
Đường tròn lớn có chu vi bằng \(8\pi \) nên bán kính của \((S)\) là \(\frac{{8\pi }}{{2\pi }} = 4.\)
Từ phương trình của \((S)\) suy ra bán kính của \((S)\) là \(\sqrt {{2^2} + {1^2} + {a^2} - 10a} .\)
Do đó \(\sqrt {{2^2} + {1^2} + {a^2} - 10a} = 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = - 1}\\{a = 11}\end{array}} \right..\) Chọn C.
Câu 29:
Tính đến đầu năm 2011, dân số toàn tỉnh Bình Phước đạt gần \[905\,\,300\] người, mức tăng dân số là \[1,37\% \] mỗi năm. Tỉnh đã thực hiện tốt chủ trương \[100\% \] trẻ em đúng độ tuổi đều vào lớp 1. Đến năm học 2024 – 2025 ngành giáo dục của tỉnh cần chuẩn bị bao nhiêu phòng học cho học sinh lớp 1, mỗi phòng dành cho 35 học sinh? (Giả sử trong năm sinh của lứa học sinh vào lớp 1 đó toàn tỉnh có \[2\,\,400\] người chết, số trẻ tử vong trước 6 tuổi không đáng kể).
 Xem đáp án
Xem đáp án
Chỉ những em sinh năm 2018 mới đủ tuổi đi học (6 tuổi) vào lớp 1 năm học 2024 - 2025.
Áp dụng công thức \({S_n} = A{\left( {1 + r} \right)^n}\) để tính dân số năm 2018.
Trong đó \(A = 905\,\,300\,;\,\,r = 1,37\% \,;\,\,n = 8\).
Dân số năm 2018 là \(905\,\,300{\left( {1 + \frac{{1,37}}{{100}}} \right)^8} = 1\,\,009\,\,411\).
Dân số năm 2017 là \(905\,\,300{\left( {1 + \frac{{1,37}}{{100}}} \right)^7} = 995\,\,769\).
Số trẻ vào lớp 1 là \(1\,\,009\,\,411 - 995\,\,769 + 2\,\,400 = 16\,\,042\).
Số phòng học cần chuẩn bị là \(16\,\,042:35 \approx 458,3\).
Vậy số phòng cần chuẩn bị là 459 phòng. Chọn C.
Câu 30:
Cho số phức \(z\) thỏa mãn \(\left| {z - 2} \right| = 2.\) Biết rằng tập hợp các điểm biểu diễn các số phức \(w = \left( {1 - i} \right)z + i\) là một đường tròn. Bán kính \(r\) của đường tròn đó là
 Xem đáp án
Xem đáp án
Cách 1: Ta có \(w = (1 - i)z + i \Leftrightarrow z = \frac{{w - i}}{{1 - i}}\)
Đặt \(w = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\)\( \Rightarrow z = \frac{{x + yi - i}}{{1 - i}}.\)
Ta có \(\left| {z - 2} \right| = 2 \Leftrightarrow \left| {\frac{{x + yi - i}}{{1 - i}} - 2} \right| = 2 \Leftrightarrow \left| {\frac{{(x + yi - i)(1 + i)}}{2} - 2} \right| = 2.\)
\( \Leftrightarrow \left| {x + xi + yi - y - i + 1 - 4} \right| = 4 \Leftrightarrow \left| {x - y - 3 + (x + y - 1)i} \right| = 4\)
\( \Leftrightarrow {\left( {x - y - 3} \right)^2} + {\left( {x + y - 1} \right)^2} = 16\)
\( \Leftrightarrow {x^2} + {y^2} + 9 - 2xy + 6y - 6x + {x^2} + {y^2} + 1 + 2xy - 2y - 2x = 16\)
\( \Leftrightarrow 2{x^2} + 2{y^2} - 8x + 4y - 6 = 0 \Leftrightarrow {x^2} + {y^2} - 4x + 2y - 3 = 0\)
Đường tròn có bán kính là \(R = \sqrt {{2^2} + {1^2} + 3} = 2\sqrt 2 .\)
Cách 2: Ta có \[w = \left( {1 - i} \right)z + i \Leftrightarrow z = \frac{{w - i}}{{1 - i}} \Leftrightarrow z - 2 = \frac{{w - i}}{{1 - i}} - 2\]
\( \Leftrightarrow z - 2 = \frac{{w - i - 2 + 2i}}{{1 - i}} = \frac{{w - 2 + i}}{{1 - i}} \Leftrightarrow \left| {z - 2} \right| = \left| {\frac{{w - 2 + i}}{{1 - i}}} \right|\).
Suy ra \(\left| {z - 2} \right| = 2 \Leftrightarrow \left| {\frac{{w - 2 + i}}{{1 - i}}} \right| = 2 \Leftrightarrow \frac{{\left| {w - 2 + i} \right|}}{{\left| {1 - i} \right|}} = 2 \Leftrightarrow \left| {w - 2 + i} \right| = 2\sqrt 2 .\) Chọn D.
Câu 31:
Cho hàm số \(f\left( x \right)\), có đồ thị hàm số \(y = f'\left( x \right)\) như hình sau:
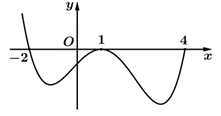
Diện tích hình phẳng giới hạn bởi trục \[Ox\] và đồ thị hàm số \(y = f'(x)\) trên đoạn \(\left[ { - 2\,;\,\,1} \right]\) và \[\left[ {1\,;\,\,4} \right]\] lần lượt bằng 9 và 12 . Khi \(f\left( 1 \right) = 3\) thì \(f\left( { - 2} \right) + f\left( 4 \right)\) bằng
 Xem đáp án
Xem đáp án
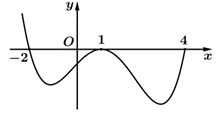
Từ đồ thị hàm số \[y = f'\left( x \right) \Rightarrow f'\left( x \right) \le 0\] trên mỗi đoạn \(\left[ { - 2\,;\,\,1} \right]\) và \[\left[ {1\,;\,\,4} \right]\].
Diện tích hình phẳng giới hạn bởi trục Ox với đồ thị hàm số \[y = f'\left( x \right)\] trên đoạn \(\left[ { - 2\,;\,\,1} \right]\)
\[{S_1} = \int\limits_{ - 2}^1 {\left| {f'\left( x \right)} \right|dx} = - \int\limits_{ - 2}^1 {f'\left( x \right)dx} = f\left( { - 2} \right) - f\left( 1 \right)\]
\( \Rightarrow f\left( { - 2} \right) - f\left( 1 \right) = 9 \Rightarrow f\left( { - 2} \right) = 9 + f\left( 1 \right) = 9 + 3 = 12\).
Diện tích hình phẳng giới hạn bởi trục \[Ox\] với đồ thị hàm số \(y = f'\left( x \right)\) trên đoạn \[\left[ {1\,;\,\,4} \right]\]
\({S_2} = \left| {f'\left( x \right)} \right|dx = - \int\limits_1^4 {f'\left( x \right)dx} = f\left( 1 \right) - f\left( 4 \right)\)
\[ \Rightarrow f\left( 1 \right) - f\left( 4 \right) = 12 \Rightarrow f\left( 4 \right) = f\left( 1 \right) - 12 = 3 - 12 = - 9\]\( \Rightarrow f\left( { - 2} \right) + f\left( 4 \right) = 12 - 9 = 3\). Chọn C.
Câu 32:
Cho tứ diện \[ABCD\] có thể tích bằng 1. Gọi \[M,{\rm{ }}N,{\rm{ }}P\] lần lượt là trọng tâm của tam giác \[ABC,{\rm{ }}ACD,{\rm{ }}ABD.\] Thể tích của tứ diện \[AMNP\] bằng
 Xem đáp án
Xem đáp án
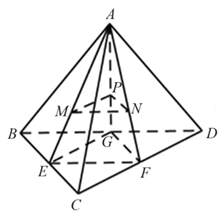
Gọi \[E,\,\,F,\,\,G\] lần lượt là trung điểm của \[BC,\,\,CD\] và \[DB.\]
Ta có \({S_{EFG}} = \frac{1}{4}{S_{BCD}} \Rightarrow {V_{A.GEF}} = \frac{1}{4}{V_{A.BCD}} = \frac{1}{4}.\)
\(\frac{{{V_{AMNP}}}}{{{V_{AEFG}}}} = \frac{{AM}}{{AE}} \cdot \frac{{AN}}{{AF}} \cdot \frac{{AP}}{{AG}} = \frac{2}{3} \cdot \frac{2}{3} \cdot \frac{2}{3} = \frac{8}{{27}}\)\( \Rightarrow {V_{AMNP}} = \frac{8}{{27}}{V_{AEFG}} = \frac{2}{{27}}.\) Chọn D.Câu 33:
Đầu tiết học, cô giáo kiểm tra bài cũ bằng cách gọi lần lượt từng người từ đầu danh sách lớp lên bảng trả lời câu hỏi. Biết rằng các bạn học sinh đầu tiên trong danh sách lớp là An, Bình, Cường với xác suất thuộc bài lần lượt là \[0,9\,;\,\,0,7\] và \[0,8.\] Cô giáo sẽ dừng kiểm tra sau khi đã có 2 học sinh thuộc bài. Tính xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên.
 Xem đáp án
Xem đáp án
• TH1: An và Cường trả lời đúng, Bình trả lời sai \( \Rightarrow {P_1} = 0,9 \cdot \left( {1 - 0,7} \right) \cdot 0,8 = 0,216\).
• TH2: Bình và Cường trả lời đúng, An trả lời sai \( \Rightarrow {P_2} = \left( {1 - 0,9} \right) \cdot 0,7 \cdot 0,8 = 0,056\).
Xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên là \(P = {P_1} + {P_2} = 0,272\). Chọn D.
Câu 34:
Cho hàm số \(y = {x^2} - 2\left( {m + \frac{1}{m}} \right)x + m\) với \(m\) là tham số thực khác 0. Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 1\,;\,\,1} \right]\) lần lượt là \({y_1},{y_2}.\) Số giá trị của \(m\) để \({y_1} - {y_2} = 8\) là
 Xem đáp án
Xem đáp án
Đặt \(y = f(x) = {x^2} - 2\left( {m + \frac{1}{m}} \right)x + m\).
Hoành độ giao điểm của đồ thị hàm số là \(x = m + \frac{1}{m} \ge 2\) (Bất đẳng thức Cô-si).
Vì hệ số \(a = 1 > 0\) nên hàm số nghịch biến trên \(\left( { - \infty \,;\,\,m + \frac{1}{m}} \right).\)
\( \Rightarrow \) Hàm số nghịch biến trên \(\left[ { - 1\,;\,\,1} \right]\)
\( \Rightarrow {y_1} = f( - 1) = 3m + \frac{2}{m} + 1\) và \({y_2} = f(1) = 1 - m - \frac{2}{m}\)
Theo đề bài ta có: \({y_1} - {y_2} = 8\)\( \Leftrightarrow 3m + \frac{2}{m} + 1 - 1 + m + \frac{2}{m} = 8\)\( \Leftrightarrow {m^2} - 2m + 1 = 0 \Leftrightarrow m = 1\).
Chọn B.
Câu 35:
Trong không gian \[Oxyz,\] cho đường thẳng \(\Delta :\frac{x}{1} = \frac{{y - 1}}{1} = \frac{z}{1}\) và hai điểm \(A\left( {0\,;\,\,1\,;\,\, - 3} \right),\) \(B\left( { - 1\,;\,\,0\,;\,\,2} \right).\) Biết điểm \(M\) thuộc đường thẳng \(\Delta \) sao cho biểu thức \(T = \left| {MA - MB} \right|\) đạt giá trị lớn nhất là \({T_{\max }}.\) Khi đó \({T_{\max }}\) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có\(A\left( {0\,;\,\,1\,;\,\, - 3} \right),\)\(B\left( { - 1\,;\,\,0\,;\,\,2} \right)\) nên \(\overrightarrow {AB} = \left( { - 1\,;\,\, - 1\,;\,\,5} \right)\).
Phương trình tham số của đường thẳng \[AB\] là \(\left\{ \begin{array}{l}x = - t\\y = 1 - t\\z = - 3 + 5t\end{array} \right.\,\,\left( {t \in \mathbb{R}} \right)\).
Xét vị trí tương đối giữa \[AB\] và \(\Delta \) ta có \[AB\] cắt \(\Delta \) tại \(C\left( { - \frac{1}{2};\frac{1}{2}; - \frac{1}{2}} \right).\)
Suy ra \(\overrightarrow {AC} = \left( { - \frac{1}{2}; - \frac{1}{2};\frac{5}{2}} \right) \Rightarrow \overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \Rightarrow C\) là trung điểm của \[AB\].
\(T = \left| {MA - MB} \right| \le AB.\) Dấu "=" xảy ra khi \(M \equiv A\) hoặc \(M \equiv B.\)
Do đó \({T_{\max }} = AB = \sqrt {27} = 3\sqrt 3 .\) Chọn C.
Câu 36:
 Xem đáp án
Xem đáp án
Vì \[A,\,\,B\] là hai tập hợp khác rỗng, nên ta có điều kiện:
\(\left\{ {\begin{array}{*{20}{l}}{m - 1 < 5}\\{3 < 2020 - 5m}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 6}\\{m < \frac{{2017}}{5}}\end{array} \Leftrightarrow m < 6} \right.} \right..\)
Để \(A\backslash B = \emptyset \) thì \(A \subset B\) ta có điều kiện
\(\left\{ {\begin{array}{*{20}{l}}{3 \le m - 1}\\{5 < 2020 - 5m}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4 \le m}\\{m < 403}\end{array} \Leftrightarrow 4 \le m < 403} \right.} \right..\)
Kết hợp điều kiện, suy ra \(4 \le m < 6.\)
Vậy có 2 giá trị nguyên của \(m\) thoả mãn yêu cầu bài toán.
Đáp án: 2.
Câu 37:
Để tăng nhiệt độ trong phòng từ \(28^\circ {\rm{C}}\), một hệ thống làm mát được phép hoạt động trong 10 phút. Gọi \(T\) (đơn vị \(^\circ C\)) là nhiệt độ phòng ở phút thứ \(t\) được cho bởi công thức \(T = - 0,008{t^3} - 0,16t + 28\) với \(t \in \left[ {1\,;\,\,10} \right].\) Nhiệt độ thấp nhất trong phòng đạt được trong thời gian 10 phút kể từ khi hệ thống bắt đầu hoạt động là bao nhiêu độ C?
 Xem đáp án
Xem đáp án
Xét hàm số \(T = - 0,008{t^3} - 0,16t + 28\) với \(t \in \left[ {1\,;\,\,10} \right].\)
Ta có \(T' = - 0,024{t^2} - 0,16\) với \(t \in \left[ {1\,;\,\,10} \right].\)
Suy ra hàm số \(T\) nghịch biến trên đoạn \(\left[ {1\,;\,\,10} \right].\)
Nhiệt độ thấp nhất trong phòng đạt được là:
\({T_{\min }} = T\left( {10} \right) = - 0,008 \cdot {10^3} - 0,16 \cdot 10 + 28 = 18,4\;\,\left( {^\circ C} \right)\).
Đáp án: \(18,4\).
Câu 38:
 Xem đáp án
Xem đáp án
Ta có \(y = {\left( {{x^3} - 6{x^2} - m} \right)^2}\)\( \Rightarrow y' = 2 \cdot \left( {3{x^2} - 12x} \right) \cdot \left( {{x^3} - 6{x^2} - m} \right)\left( {{{\left( {{u^2}} \right)}^\prime } = 2u \cdot u'} \right)\).
Khi đó \(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{3{x^2} - 12x = 0}\\{{x^3} - 6{x^2} - m = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0\,;\,\,x = 4}\\{m = {x^3} - 6{x^2} = f\left( x \right)}\end{array}} \right.} \right.\).
Yêu cầu bài toán \( \Leftrightarrow m = f\left( x \right)\) có ba nghiệm phân biệt.
Dựa vào bảng biến thiên của hàm số \(f\left( x \right) \Rightarrow - 32 < m < 0.\)
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 31\,;\,\, - 30\,;\,\, - 29\,;\,\, \ldots \,;\,\, - 1} \right\}.\)
Đáp án: 31.
Câu 39:
Cho một đa giác đều có \[2n\] đỉnh \(\left( {n \ge 2\,,\,\,n \in {\mathbb{N}^*}} \right).\) Chọn ngẫu nhiên ba đỉnh trong số 2n đỉnh của đa giác đó, biết xác suất ba đỉnh được chọn tạo thành một tam giác vuông là \[0,2.\] Giá trị \(n\) bằng
 Xem đáp án
Xem đáp án
Số tam giác tạo thành khi chọn ngẫu nhiên 3 điểm là \(C_{2n}^3\).
Số đường chéo đi qua tâm là \(n\).
Suy ra, số hình chữ nhật nhận 2 đường chéo đi qua tâm làm 2 đường chéo là \(C_n^2\).
Số tam giác vuông được tạo thành là \(4C_n^2\).
Khi đó, ta được phương trình \(\frac{{4 \cdot C_n^2}}{{C_{2n}^3}} = 0,2 \Rightarrow n = \frac{1}{8}\).
Đáp án: \(\frac{1}{8}\).
Câu 40:
Biết \(\mathop {\lim }\limits_{x \to 3} \frac{{x + 1 - \sqrt {5x + 1} }}{{x - \sqrt {4x - 3} }} = \frac{a}{b}\) với \[a,\,\,b\] là số nguyên dương và \(\frac{a}{b}\) là phân số tối giản. Tính giá trị của biểu thức \(T = a - b.\)
 Xem đáp án
Xem đáp án
Ta có \(\mathop {\lim }\limits_{x \to 3} \frac{{x + 1 - \sqrt {5x + 1} }}{{x - \sqrt {4x - 3} }}\)\( = \mathop {\lim }\limits_{x \to 3} \frac{{\left[ {{{\left( {x + 1} \right)}^2} - 5x + 1} \right]\left( {x + \sqrt {4x - 3} } \right)}}{{\left( {{x^2} - 4x + 3} \right)\left( {x + 1 + \sqrt {5x + 1} } \right)}}\)
\( = \mathop {\lim }\limits_{x \to 3} \frac{{\left( {{x^2} - 3x} \right)\left( {x + \sqrt {4x - 3} } \right)}}{{\left( {{x^2} - 4x + 3} \right)\left( {x + 1 + \sqrt {5x + 1} } \right)}}\)\( = \mathop {\lim }\limits_{x \to 3} \frac{{x\left( {x + \sqrt {4x - 3} } \right)}}{{\left( {x - 1} \right)\left( {x + 1 + \sqrt {5x + 1} } \right)}} = \frac{9}{8}{\rm{ }}\)
Do đó \(\left\{ {\begin{array}{*{20}{l}}{a = 9}\\{b = 8}\end{array} \Rightarrow T = a - b = 1} \right.\).
Đáp án: 1.
Câu 41:
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} - 2x + 2m}}{{\left( {x - 1} \right)\left( {x + m} \right)}}.\) Có bao nhiêu giá trị của \(m\) để đồ thị hàm số có duy nhất một tiệm cận đứng?
 Xem đáp án
Xem đáp án
Đặt \(g(x) = {x^2} - 2x + 2m.\)
− Khi \(m = - 1\) ta có hàm số \(y = f(x) = \frac{{{x^2} - 2x - 2}}{{{{\left( {x - 1} \right)}^2}}}.\)
− Khi đó \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 2x - 2}}{{{{\left( {x - 1} \right)}^2}}} = - \infty \) suy ra đồ thị của hàm số đã cho có duy nhất một tiệm cận đứng là \(x = 1.\)
− Khi \(m \ne 1\), xét hàm số \[y = f(x) = \frac{{{x^2} - 2x + 2m}}{{\left( {x - 1} \right)\left( {x + m} \right)}}\].
• TH1: Đồ thị hàm số đã cho có duy nhất một tiệm cận đứng \(x = 1.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{g(1) \ne 0}\\{g( - m) = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 1 + 2m \ne 0}\\{{m^2} + 4m = 0}\end{array} \Leftrightarrow \left\{ \begin{array}{l}m \ne \frac{1}{2}\\\left[ \begin{array}{l}m = 0\\m = - 4\end{array} \right.\end{array} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 0}\\{m = - 4}\end{array}} \right.} \right.} \right.\)
• TH2: Đồ thị hàm số đã cho có duy nhất một tiệm cận đứng \(x = m.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{g(1) = 0}\\{g( - m) \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 + 2m = 0}\\{{m^2} + 4m \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m = \frac{1}{2}}\\{m \ne 0}\\{m \ne - 4}\end{array} \Leftrightarrow m = \frac{1}{2}.} \right.} \right.} \right.\)
Vậy có 4 giá trị của \(m\) thoả mãn yêu cầu bài toán.
Đáp án: 4.
Câu 42:
 Xem đáp án
Xem đáp án
Ta có \[f'\left( x \right)\left[ {1 + {e^{f\left( x \right)}}} \right] = 1 + {e^x} \Rightarrow f'\left( x \right) + f'\left( x \right)\,{e^{f\left( x \right)}} = 1 + {e^x}\]
\( \Rightarrow {\left[ {f\left( x \right) + {e^{f\left( x \right)}}} \right]^\prime } = 1 + {e^x}\)\( \Rightarrow \int {{{\left[ {f\left( x \right) + {e^{f\left( x \right)}}} \right]}^\prime }} {\rm{d}}x = \int {\left( {1 + {e^x}} \right)\,} {\rm{d}}x\)
\( \Rightarrow f\left( x \right) + {e^{f\left( x \right)}} = x + {e^x} + C\).
Lại có \(f\left( 0 \right) = 0 \Rightarrow C = 0 \Rightarrow f(x) + {e^{f\left( x \right)}} = x + {e^x}.\)
Xét hàm số \(g(t) = t + {e^t}\) với \(t \in \mathbb{R}.\)
Ta có \(g'\left( t \right) = 1 + {e^t} > 0,\,\,\forall t \in \mathbb{R}\) nên \(g\left( t \right)\) đồng biến trên.
Suy ra \(f\left( x \right) + {e^{f\left( x \right)}} = x + {e^x} \Rightarrow f\left( x \right) = x.\)
Do đó diện tích hình phẳng đó là: \(S = \int\limits_1^3 {x\;{\rm{d}}x} = \left. {\frac{1}{2}{x^2}} \right|_1^3 = 4.\)
Đáp án: 4.
Câu 43:
 Xem đáp án
Xem đáp án
Gọi \(\overrightarrow {{u_1}} = \left( {1\,;\,\,1\,;\,\,2} \right)\,,\,\,\overrightarrow {{u_2}} = \left( {2\,;\,\,1\,;\,\,1} \right)\) lần lượt là một vectơ chỉ phương của \[{d_1},\,{d_2}.\]
Gọi \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {{u_1}} ,\,\,\overrightarrow {{u_2}} } \right] = \left( { - 1\,;\,\,3\,;\,\, - 1} \right)\), có
\(\overrightarrow {{n_1}} \) cùng phương với \(\overrightarrow {{n_2}} = \left( {1\,;\,\, - 3\,;\,\,1} \right).\)
\(\vec n = \left( {1\,;\,\,a\,;\,\,b} \right)\) là một vectơ chỉ phương của \(\left( P \right)\).
Do \(\left( P \right)\) song song với \({d_1},\,\,{d_2}\) nên chọn \(\vec n = \left( {1\,;\,\, - 3\,;\,\,1} \right).\)
Do đó, phương trình mặt phẳng \(\left( P \right)\) có dạng: \(x - 3y + z + c = 0.\)
Lấy \({M_1}\left( {1\,;\,\, - 2\,;\,\,1} \right) \in {d_1},\,\,{M_2}\left( {1\,;\,\,1\,;\,\, - 2} \right) \in {d_2}\).
Có \(d\left( {{d_1}\,,\,\,\left( P \right)} \right) = 2d\left( {{d_2}\,,\,\,\left( P \right)} \right) \Leftrightarrow d\left( {{M_1}\,,\,\,\left( P \right)} \right) = 2d\left( {{M_2}\,,\,\,\left( P \right)} \right)\)
\( \Leftrightarrow \frac{{\left| {1 - 3 \cdot \left( { - 2} \right) + 1 + c} \right|}}{{\sqrt {11} }} = 2\frac{{\left| {1 - 3 - 2 + c} \right|}}{{\sqrt {11} }}\)\[ \Leftrightarrow \left| {8 + c} \right| = 2\left| { - 4 + c} \right|\]\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{8 + c = 2\left( { - 4 + c} \right)}\\{8 + c = 2\left( {4 - c} \right)}\end{array}} \right.\]\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{c = 16\,\,(TM)}\\{c = 0\,\,(L)}\end{array}} \right.\)
Do đó \((P):x - 3y + z + 16 = 0 \Rightarrow a = - 3,\,\,b = 1,\,\,c = 16.\)
Vậy \(a + b + c = 14.\)
Đáp án: 14.
Câu 44:
 Xem đáp án
Xem đáp án
Đặt \(t = {\log _3}x \Rightarrow x = {3^t}.\)
Phương trình trở thành: \({t^2} + 3m(1 + t) + 2{m^2} - 2m - 1 = 0\)\( \Leftrightarrow {t^2} + 3mt + 2{m^2} + m - 1 = 0\)
Ta có \(\Delta = {(m - 2)^2} \Rightarrow \left[ {\begin{array}{*{20}{l}}{{t_1} = \frac{{ - 3m + m - 2}}{2} = - m - 1}\\{{t_2} = \frac{{ - 3m - m + 2}}{2} = - 2m + 1}\end{array}} \right.\).
Khi đó \({t_1} = {\log _3}{x_1}\) và \({t_2} = {\log _3}{x_2}\).
Mà \({x_1} + {x_2} < \frac{{10}}{3} \Leftrightarrow {3^{ - m - 1}} + {3^{ - 2m + 1}} < \frac{{10}}{3}\)\( \Leftrightarrow \frac{{{3^{ - m}}}}{3} + 3 \cdot {\left( {{3^{ - m}}} \right)^2} < \frac{{10}}{3}\).
Đặt \({3^{ - m}} = u > 0\)
\({\rm{ (1) }} \Leftrightarrow 3{u^2} + \frac{u}{3} - \frac{{10}}{3} < 0 \Leftrightarrow \frac{{ - 10}}{9} < u < 1\)\( \Leftrightarrow - \frac{{10}}{9} < {3^{ - m}} < 1 \Leftrightarrow - m < 0 \Leftrightarrow m > 0\).
Để phương trình có hai nghiệm phân biệt thì \(\Delta > 0 \Leftrightarrow m \ne 2\). Vậy \(S\) có vô số phần tử.
Đáp án: Vô số.
Câu 45:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình sau:
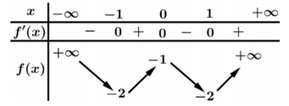
Biết \(f\left( { - 2} \right) = 7\), hỏi có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {{x^2} - 1} \right| - 2} \right) = m\) có đúng 6 nghiệm phân biệt?
 Xem đáp án
Xem đáp án
Xét hàm số \(u = \left| {{x^2} - 1} \right| - 2 \Rightarrow u' = \frac{{{x^2} - 1}}{{\left| {{x^2} - 1} \right|}} \cdot 2x\) \( \Rightarrow \) Hàm số đạt cực trị tại \(x = 0\,;\,\,x = \pm 1.\)
Ta có bảng biến thiên:
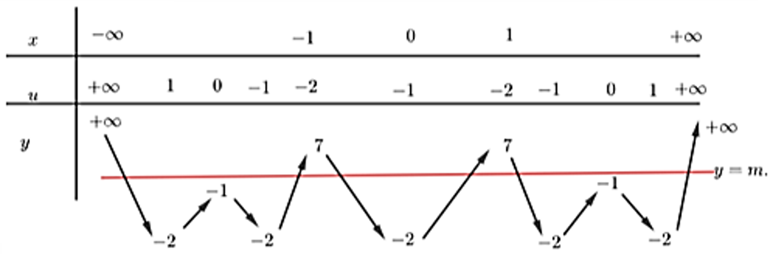
Dựa vào BBT, để phương trình \(f\left( {\left| {{x^2} - 1} \right| - 2} \right) = m\) có đúng 6 nghiệm \( \Rightarrow m \in \left( { - 1\,;\,\,7} \right).\)
Vậy có 7 giá trị \(m\) thoả mãn yêu cầu bài toán.
Đáp án: 7.
Câu 46:
Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x - 5}}{2} = \frac{{y + 7}}{2} = \frac{{z - 12}}{{ - 1}}\) và mặt phẳng \((\alpha ):x + 2y - 3z - 3 = 0.\) Gọi \(M\) là giao điểm của \(d\) và \((\alpha ),\,\,A\) thuộc \(d\) sao cho \(AM = \sqrt {14} .\) Khoảng cách từ \(A\) đến mặt phẳng \((\alpha ).\)
 Xem đáp án
Xem đáp án
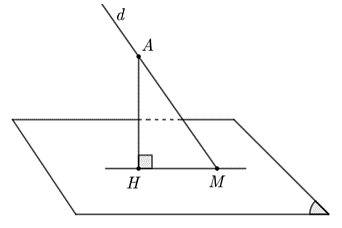
Đường thẳng \(d:\frac{{x - 5}}{2} = \frac{{y + 7}}{2} = \frac{{z - 12}}{{ - 1}}\) có một vectơ chỉ phương là \(\vec u = \left( {2\,;\,\,2\,;\,\, - 1} \right).\)
Mặt phẳng \((\alpha ):x + 2y - 3z - 3 = 0\) có một vectơ pháp tuyến là \(\vec n = \left( {1\,;\,\,2\,;\,\, - 3} \right).\)
Ta có \[\sin \left( {d\,,\,\,(\alpha )} \right) = \frac{{\left| {\vec u \cdot \vec n} \right|}}{{\left| {\vec u} \right| \cdot \left| {\vec n} \right|}} = \frac{{3\sqrt {14} }}{{14}}.\]
Gọi \(H\) là hình chiếu vuông góc của \(A\) lên mặt phẳng \((\alpha ).\)
Khi đó tam giác \[MAH\] vuông tại \(H\) nên
\(\sin \left( {d\,,\,\left( \alpha \right)} \right) = \sin \widehat {AMH} = \frac{{AH}}{{AM}}\)\( \Rightarrow AH = AM \cdot \sin \left( {d\,,\,\left( \alpha \right)} \right) = 3.\)
Vậy khoảng cách từ \(A\) đến mặt phẳng \((\alpha )\) bằng 3.
Đáp án: 3.
Câu 47:
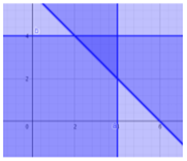
Cho \[X\] là tập hợp tất cả các số phức \[z\] có phần thực và phần ảo không vượt quá 4, đồng thời tổng của phần thực và phần ảo không nhỏ hơn 6. Gọi m là môđun nhỏ nhất của các số phức trong \[X\] và \[M\] là môđun lớn nhất của các số phức trong \[X.\] Hỏi giá trị của tích \[M \cdot m\] bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đặt \(z = x + yi\quad (x,y \in \mathbb{R})\)
Theo bài ra, ta có \(x \le 4,\,\,y \le 4\) và \(x + y \ge 6.\)
Vẽ các đường thẳng \(x = 4,\,\,y = 4\) và \(x + y = 6\) trên hệ toạ độ \[Oxy.\]
Vẽ các miền phẳng thoả mãn \(x \le 4,\,\,y \le 4\) và \(x + y - 6 \ge 0.\)
Dễ thấy, phần giao nhau của 3 miền trên là tam giác xanh đậm.
Với toạ độ các đỉnh là \(A\left( {4\,;\,\,4} \right),\,\,B\left( {4\,;\,\,2} \right)\) và \(C\left( {2\,;\,\,4} \right).\)
Ta có \(\left| z \right| = OM\) với \(M\) là điểm biểu diễn số phức \(z\).
Khi đó, điểm \(M\) nằm trong tam giác \[ABC\].
Gọi \(H\left( {3\,;\,\,3} \right)\) là trung điểm của \(BC \Rightarrow O,\,\,A,\,\,H\) thẳng hàng
Suy ra \({\left| z \right|_{\max }} = O{M_{\max }} = OA = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 .\)
Và \({\left| z \right|_{\min }} = O{M_{\min }} = OH = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 .\)
Vậy \(M \cdot m = 4\sqrt 2 \cdot 3\sqrt 2 = 24.\)
Đáp án: 24.
Câu 48:
Có bao nhiêu cặp số nguyên dương \(\left( {x;\,\,y} \right)\) thỏa mãn
\({\log _3}\left( {{x^2} + y + 3x} \right) + {\log _2}\left( {{x^2} + y} \right) \le {\log _3}x + {\log _2}\left( {{x^2} + y + 18x} \right)?\)
 Xem đáp án
Xem đáp án
\({\log _3}\left( {{x^2} + y + 3x} \right) + {\log _2}\left( {{x^2} + y} \right) \le {\log _3}x + {\log _2}\left( {{x^2} + y + 18x} \right)\)
\( \Leftrightarrow {\log _3}\left( {\frac{{{x^2} + y + 3x}}{x}} \right) - {\log _2}\left( {\frac{{{x^2} + y + 18x}}{{{x^2} + y}}} \right) \le 0\)\( \Leftrightarrow {\log _3}\left( {3 + \frac{{{x^2} + y}}{x}} \right) - {\log _2}\left( {1 + \frac{{18x}}{{{x^2} + y}}} \right) \le 0\,\,\,(*)\)
Đặt \(t = \frac{{{x^2} + y}}{x}\). Khi đó \((*) \Leftrightarrow {\log _3}(3 + t) - {\log _2}\left( {1 + \frac{{18}}{t}} \right) \le 0(1)\)
Xét hàm \(f(t) = {\log _3}(3 + t) - {\log _2}\left( {1 + \frac{{18}}{t}} \right),\)\(\,\,f'(t) = \frac{1}{{(3 + t)\ln 3}} + \frac{{18}}{{\left( {{t^2} + 18t} \right)\ln 2}} > 0,\,\,\forall t > 0\)
Suy ra hàm số đồng biến trên \(\left( {0\,;\,\, + \infty } \right)\).
Lại có \(f(6) = 0 \Rightarrow (1) \Leftrightarrow f(t) \le f(6) \Leftrightarrow t \le 6\) hay \(\frac{{{x^2} + y}}{x} \le 6\)
\[ \Leftrightarrow {x^2} + y - 6x \le 0 \Leftrightarrow 9 - y \ge {\left( {x - 3} \right)^2}.\]
Cho \(y\) ứng với các số nguyên dương từ 0 đến 9 ta được 35 cặp giá trị thoả mãn.
Vậy có 35 cặp số nguyên dương \(\left( {x\,;\,\,y} \right)\) thỏa mãn yêu cầu bài toán.
Đáp án: \[\frac{3}{5}\].
Câu 49:
Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh 2, SA vuông góc với đáy và khoảng cách từ \(C\) đến mặt phẳng \(\left( {SBD} \right)\) bằng \(\frac{{2\sqrt 3 }}{3}.\) Thể tích của khối chóp đó là
 Xem đáp án
Xem đáp án
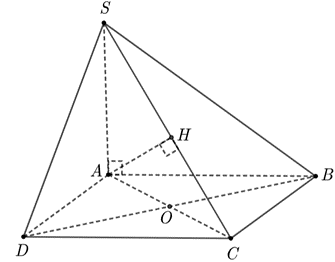
Gọi \(O = AC \cap BD\,;\,\,H\) là hình chiếu của \(A\) lên \[SO.\]
Vì \(O\) là trung điểm của AC nên \(d\left( {C,\,\,\left( {SBD} \right)} \right) = d\left( {A,\,\,\left( {SBD} \right)} \right)\)
Ta có \(BD \bot AC\,;\,\,BD \bot SA \Rightarrow BD \bot \left( {SAC} \right)\)
\( \Rightarrow \left( {SBD} \right) \bot \left( {SAC} \right).\)
\(SO = \left( {SAC} \right) \cap \left( {SBD} \right)\)
\(AH \bot SO \Rightarrow AH \bot (SBD) \Rightarrow AH = d\left( {A,\left( {SBD} \right)} \right) = d\left( {C,\left( {SBD} \right)} \right) = \frac{{2\sqrt 3 }}{3}{\rm{. }}\)
Ta có \(AO = \sqrt 2 .\) Xét tam giác \[SAO\] có \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{O^2}}}\)
\( \Rightarrow \frac{1}{{S{A^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{O^2}}} = \frac{3}{4} - \frac{1}{2} = \frac{1}{4} \Rightarrow SA = 2\)
Thể tích của khối chóp là \({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SA = \frac{8}{3}.\)
Đáp án: \(\frac{8}{3}\).
Câu 50:
Cho khối tứ diện \[ABCD\] có cạnh \[AC\] và \[BD\] thoả mãn \(A{C^2} + B{D^2} = 16\) và các cạnh còn lại đều bằng 6. Thể tích khối tứ diện \[ABCD\] đạt giá trị lớn nhất bằng bao nhiêu? (kết quả làm tròn đến chữ số hàng đơn vị).
 Xem đáp án
Xem đáp án
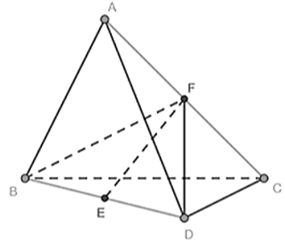
Gọi \[E,\,\,F\] lần lượt là trung điểm của \[BD,\,\,AC.\]
Giả sử \[AC = a\,;\,\,BD = b\], theo giả thiết ta có \({a^2} + {b^2} = 16\,\,(a,b > 0)\)
Xét \(\Delta ABC\) và \(\Delta ADC\) có: AC chung; \(AB = AD\); \(BC = CD\).
Do đó \(\Delta ABC = \Delta ADC\,\,(c.c.c)\)
Suy ra \(BF = GF\) (hai trung tuyến tương ứng).
Ta có \(BF = \sqrt {A{B^2} - A{F^2}} = \sqrt {{6^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \sqrt {36 - \frac{{{a^2}}}{4}} \)
\(EF = \sqrt {B{F^2} - B{E^2}} = \sqrt {36 - \frac{{{a^2}}}{4} - \frac{{{b^2}}}{4}} = \sqrt {36 - \frac{{16}}{4}} = \sqrt {32} \)
\( \Rightarrow {S_{BDF}} = \frac{1}{2}EF \cdot BD = \frac{1}{2} \cdot \sqrt {32} \cdot b = 2\sqrt 2 b\)
Lại có \(\left\{ {\begin{array}{*{20}{l}}{AC \bot BF}\\{AC \bot DF}\end{array} \Rightarrow AC \bot \left( {BDF} \right)} \right.\).
Khi đó \({V_{ABCD}} = {V_{A.BDF}} + {V_{C.BDF}}\)\( = \frac{1}{3}AF \cdot {S_{BDF}} + \frac{1}{3} \cdot CF \cdot {S_{BDF}}\)
\( = \frac{1}{3} \cdot {S_{BDF}} \cdot \left( {AF + CF} \right) = \frac{1}{3} \cdot {S_{BDF}} \cdot AC\)\( = \frac{1}{3}a \cdot 2\sqrt 2 b = \frac{{2\sqrt 2 }}{3}ab\).
Áp dụng bất đẳng thức Côsi, ta có: \(ab \le \frac{{{a^2} + {b^2}}}{2} = \frac{{16}}{2} = 8 \Rightarrow {V_{ABCD}} \le \frac{{2\sqrt 2 }}{3}.8 = \frac{{16\sqrt 2 }}{3}\).
Vậy \({V_{\max }} = \frac{{16\sqrt 2 }}{3} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = b}\\{{a^2} + {b^2} = 16}\end{array} \Leftrightarrow a = b = 2\sqrt 2 } \right..\)
Đáp án: \[\frac{{16\sqrt 2 }}{3}\].
Câu 51:
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Hai câu thơ: “Ôi con sóng ngày xưa/ Và ngày sau vẫn thế” khẳng định sự vĩnh hằng bất biến, khẳng định quy luật muôn đời của những con sóng. Dù là “ngày xưa” (quá khứ) hay “ngày sau” (tương lai) thì con sóng “vẫn thế” (không thay đổi). Chọn A.
Câu 52:
 Xem đáp án
Xem đáp án
“Bồi hồi” có nghĩa là ở trong trạng thái có những cảm xúc, ý nghĩ trở đi trở lại, làm xao xuyến không yên (thường là khi nghĩ đến việc đã qua). Chọn B.
Câu 53:
 Xem đáp án
Xem đáp án
Ý nghĩa của trật tự từ “anh – em” trong câu thơ “Em nghĩ về anh, em” là thể hiện người con gái luôn nghĩ cho người mình yêu trước. Trong suốt bài thơ, hình tượng “em” hiện lên với những trăn trở, suy tư cho “anh” và cho tình yêu của đôi lứa. Chọn C.
Câu 54:
 Xem đáp án
Xem đáp án
Câu 55:
Chủ đề nổi bật của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Chủ đề nổi bật của đoạn trích là thể hiện quy luật của sóng và tình yêu. Nếu như con sóng ngoài biển khơi vẫn ngày đêm vỗ vào bờ thì khao khát tình yêu trong “em” cũng trường tồn, bất diệt như sự tồn tại của sóng trong tự nhiên. Chọn A.
Câu 56:
 Xem đáp án
Xem đáp án
Đoạn thơ được viết theo thể thơ tự do. Các dòng linh hoạt về số câu, số chữ,… Chọn B.
Câu 58:
Chủ đề của đoạn thơ là gì?
 Xem đáp án
Xem đáp án
Chủ đề của đoạn thơ nói về những đóng góp, hi sinh thầm lặng của Nhân dân đối với Đất Nước. Chọn A.
Câu 59:
Trong đoạn thơ, từ ngữ nào mang nghĩa “kiến tạo, tạo tác, hình thành”?
 Xem đáp án
Xem đáp án
Từ “đắp” là từ mang nghĩa “kiến tạo, tạo tác, hình thành”. Chọn D.
Câu 60:
. Trong đoạn thơ, từ ngữ nào mang nghĩa “chuyển giao” từ thế hệ trước sang thế hệ sau?
 Xem đáp án
Xem đáp án
Câu 61:
Văn bản trên được viết theo thể thơ gì?
 Xem đáp án
Xem đáp án
Văn bản trên được viết theo thể thơ thất ngôn (thơ 7 chữ). Chọn C.
Câu 62:
Nêu nội dung cơ bản của tám câu thơ đầu trong đoạn trích.
 Xem đáp án
Xem đáp án
Nội dung cơ bản của 8 câu thơ đầu là: Văn bản tập trung khắc họa chân dung người chiến sĩ Tây Tiến (ngoại hình, tâm hồn, lí tưởng, sự hi sinh). Chọn A.
Câu 63:
Từ “Tây Tiến” được lặp lại nhiều lần trong đoạn trích có tác dụng:
 Xem đáp án
Xem đáp án
Từ “Tây Tiến” được lặp lại ba lần trong đoạn thơ. Việc lặp lại ba lần từ “Tây Tiến” trong đoạn thơ cho ta hình dung nỗi nhớ Tây Tiến trong lòng nhà thơ là da diết, nó cứ trở đi trở lại trong lòng nhà thơ. Phép lặp này cũng cho chúng ta ấn tượng sâu sắc về hình ảnh trung tâm của nỗi nhớ trong lòng nhà thơ. Chọn D.
Câu 64:
Từ “Tây Tiến” được lặp lại nhiều lần trong đoạn trích có tác dụng:
 Xem đáp án
Xem đáp án
Từ “Tây Tiến” được lặp lại ba lần trong đoạn thơ. Việc lặp lại ba lần từ “Tây Tiến” trong đoạn thơ cho ta hình dung nỗi nhớ Tây Tiến trong lòng nhà thơ là da diết, nó cứ trở đi trở lại trong lòng nhà thơ. Phép lặp này cũng cho chúng ta ấn tượng sâu sắc về hình ảnh trung tâm của nỗi nhớ trong lòng nhà thơ. Chọn D.
Câu 65:
 Xem đáp án
Xem đáp án
Phép tu từ nói giảm được thể hiện trong câu thơ: “Áo bào thay chiếu anh về đất”. Cụm từ “về đất” được thay thế cho sự chết chóc, hi sinh. Chọn B.
Câu 66:
 Xem đáp án
Xem đáp án
Câu 67:
Phương thức biểu đạt chính của đoạn trích trên là gì?
 Xem đáp án
Xem đáp án
Văn bản đưa ra suy nghĩ của tác giả về tình yêu quê hương và lập luận về ý kiến của mình => phương thức biểu đạt nghị luận. Chọn A.
Câu 68:
Nhận định nào sau đây KHÔNG có trong đoạn trích?
 Xem đáp án
Xem đáp án
Câu 69:
 Xem đáp án
Xem đáp án
Dựa vào câu “Không phải ngẫu nhiên trong tiếng Việt, khi những cặp vợ chồng chung thủy yêu nhau, thì lúc hạnh phúc nhất họ thường tha thiết gọi nhau là “nhà ơi””. Chọn C.
Câu 70:
 Xem đáp án
Xem đáp án
Dựa vào câu “Từng không biết bao lần, cái Kinh Thành oanh liệt này đã ngun ngút cháy khi phải đối đầu với đủ mọi thế lực ngoại xâm...”. Chọn C.
Câu 71:
Chủ đề của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Dựa vào ý chính của văn bản là nói lên những tình cảm cá nhân, gia đình gắn liền với tình yêu quê hương, đất nước. Chọn B.
Câu 72:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Ngày 17/01, Tòa án nhân dân Thành phố Hà Nội tuyên phạt rất nặng vợ chồng bị cáo Nguyễn Ngọc Cường (SN 1989) và Trần Mỹ Ngọc (SN 1988, ở Long Biên) lần lượt mức án 9 năm và 6 năm, 6 tháng tù vì tội làm, tàng trữ, vận chuyển, lưu hành tiền giả.
 Xem đáp án
Xem đáp án
Đoạn trích trên sử dụng phong cách ngôn ngữ báo chí đưa tin về vấn đề pháp luật vì vậy không thể dùng từ mang sắc thái biểu cảm gây hiểu nhầm về nghĩa.
Tòa chỉ tuyên phạt mức án theo quy định của pháp luật nên không đánh giá “nặng” hay “nhẹ”, do đó, sử dụng từ “rất nặng” là sai phong cách ngôn ngữ. Chọn A.
Câu 73:
Bài thơ Sang thu được sáng tác năm 1977, thể hiện những cảm nhận tinh tế của tác giả trước những chuyển đổi của thiên nhiên, sức sống của tạo vật trong những khoảnh khắc giao mùa.
 Xem đáp án
Xem đáp án
Câu 74:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Đọc bài thơ Chiều tối, chúng ta không chỉ cảm nhận được dòng suy tư riêng tư của Người, mà còn hiểu được sâu sắc dòng tâm trạng của Nguyễn Ái Quốc trong bước lưu chuyển của vũ trụ, cuộc sống.
 Xem đáp án
Xem đáp án
Câu 75:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Những chiếc xe vẫn bon bon chạy trên con đường gồ ghề, gập ghềnh, khúc khuỷu.
 Xem đáp án
Xem đáp án
Câu 76:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Nguyễn Đình Chiểu là nhà thơ có quan niệm văn chương đồng nhất. Ông chủ trương dùng văn chương biểu hiện đạo lí và chiến đấu cho sự nghiệp chính nghĩa.
 Xem đáp án
Xem đáp án
Câu 77:
Chọn một tác phẩm KHÔNG cùng nhóm với các tác phẩm còn lại.
 Xem đáp án
Xem đáp án
Câu 78:
 Xem đáp án
Xem đáp án
Đối với dạng đề này, HS cần có kiến thức về vốn từ.
Phun: làm cho chất lỏng hoặc chất hơi bị đẩy mạnh ra ngoài thành tia qua lỗ hẹp.
Hút: làm cho chất lỏng, chất khí chuyển chỗ về phía nào đó bằng cách tạo ra ở đó một khoảng chân không.
Xả: thải hơi hoặc nước ra ngoài.
Tháo: làm cho các chi tiết, bộ phận được lắp ghép rời ra khỏi chỉnh thể.
Như vậy, cả A, C và D đều có ý diễn tả một chất/bộ phận thoát ra rời ra ngoài, riêng B là thu/chuyển chỗ về. Chọn B.
Câu 79:
 Xem đáp án
Xem đáp án
Câu 80:
 Xem đáp án
Xem đáp án
Câu 81:
 Xem đáp án
Xem đáp án
Câu 82:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
hình thành và phát triển trong bối cảnh văn hóa, văn học vùng Đông Á, Đông Nam Á; có quan hệ giao lưu với nhiều nền văn học khu vực, đặc biệt là văn học Trung Quốc.
 Xem đáp án
Xem đáp án
Câu 83:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Các dòng không khí di chuyển những đám mây khắp toàn cầu, ________ phân tử mây va chạm vào nhau, _________ với nhau, gia tăng kích cỡ và rơi xuống thành mưa.
 Xem đáp án
Xem đáp án
- kết hợp: gắn với nhau để bổ sung, hỗ trợ cho nhau.
- tạo: làm ra, từ chỗ không có trở thành có và tồn tại.
- cộng hưởng: dao động với biên độ rất lớn.
- bổ sung: thêm vào cho đủ.
Trong 4 từ trên, chỉ có từ kết hợp khi điền vào chỗ trống thứ 2 diễn tả đúng nhất ý nghĩa của câu. → Chọn A.
Câu 84:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Văn Nguyễn Thi vừa giàu chất , đầy những chi tiết dữ dội, ác liệt của chiến tranh, vừa đằm thắm chất trữ tình với một ngôn ngữ phong phú, góc cạnh, đậm chất Nam Bộ, có khả năng tạo nên những nhân vật có cá tính mạnh mẽ.
 Xem đáp án
Xem đáp án
Câu 85:
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Hàng triệu người Argentina đổ ra đường ______ cúp vàng World Cup.
 Xem đáp án
Xem đáp án
Các từ “đỡ”, “khiêng”, “nâng” đơn thuần thể hiện hành động đưa lên cao, nâng và chuyển vật nặng hoặc cồng kềnh bằng sức của hai hay nhiều người hợp lại… cũng như không phù hợp ngữ cảnh của hoạt động. Động từ “rước” có nghĩa là đi thành đoàn có cờ trống, đèn đuốc, v.v. để làm lễ đón về hoặc để biểu thị sự vui mừng, phấn khởi trong ngày hội. → Từ phù hợp là từ “rước”
=> Hàng triệu người Argentina đổ ra đường rước cúp vàng World Cup. Chọn D.
Câu 86:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Tây Tiến – sự thăng hoa của một tâm hồn ________.
 Xem đáp án
Xem đáp án
Câu 87:
Câu thơ “Chiến trường đi chẳng tiếc đời xanh” mang ý nghĩa gì?
 Xem đáp án
Xem đáp án
Câu 88:
Cụm từ “Kìa em” trong đoạn trích trên thể hiện tâm trạng gì của những người lính Hà thành trước vẻ đẹp của các cô gái trong đêm hội?
 Xem đáp án
Xem đáp án
Câu 89:
Hình ảnh “đôi mắt chị bóng tối ngập đầy dần” diễn tả điều gì?
 Xem đáp án
Xem đáp án
Câu 90:
Phong cách ngôn ngữ của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Đoạn trích trên thuộc phong cách ngôn ngữ nghệ thuật. Chọn C.
Câu 91:
Việc nêu tên các sáng tác và các thể loại văn chương cho thấy đặc điểm nào trong tính cách của nhân vật trữ tình - tác giả Tản Đà - trong đoạn thơ?
 Xem đáp án
Xem đáp án
Câu 92:
Câu thơ “Áo bào thay chiếu anh về đất” sử dụng phép tu từ gì?
 Xem đáp án
Xem đáp án
Câu 93:
Tác giả sử dụng biện pháp tu từ nghệ thuật gì trong câu văn: “Chúng tắm các cuộc khởi nghĩa của ta trong những bể máu”?
 Xem đáp án
Xem đáp án
Câu 94:
Cụm từ “biệt nhỡn liên tài” được in đậm trong đoạn trích trên có ý nghĩa gì?
 Xem đáp án
Xem đáp án
Câu 95:
Phong cách ngôn ngữ của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Câu 96:
Lời văn thể hiện thái độ như thế nào của vua Quang Trung với người hiền khi ban chiếu cầu hiền?
 Xem đáp án
Xem đáp án
Câu 97:
Câu văn “Cô ấy là vợ A Sử, con trai thống lý” có ý nghĩa gì?
 Xem đáp án
Xem đáp án
Câu 98:
Trong đoạn trích trên, “một cái gì mới vừa vỡ ra trong đầu vị Bao Công của cái phố huyện vùng biển” là điều gì?
 Xem đáp án
Xem đáp án
Câu 99:
Nội dung chính của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Câu 100:
Phong cách ngôn ngữ của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Câu 101:
Cách kể trong đoạn trích có tác dụng gì?
 Xem đáp án
Xem đáp án
Câu 102:
PHẦN 3: KHOA HỌC
Lĩnh vực: Khoa học tự nhiên và xã hội (50 câu – 60 phút)
Câu 101. Cuộc khai thác thuộc địa lần thứ nhất (1897-1914) của thực dân Pháp đã đưa tới lực lượng mới nào trong xã hội Việt Nam có thành phần xuất thân phức tạp nhất?
 Xem đáp án
Xem đáp án
Câu 103:
 Xem đáp án
Xem đáp án
Câu 104:
Trong các quốc gia sau đây, quốc gia nào ở châu Phi giành được độc lập sau Chiến tranh thế giới thứ hai?
 Xem đáp án
Xem đáp án
Phương án A, B, D đều là các quốc gia ở khu vực Mĩ Latinh.
Phương án C đúng, Anggôla là quốc gia ở châu Phi và giành được độc lập sau Chiến tranh thế giới thứ hai. Chọn C.
Câu 105:
 Xem đáp án
Xem đáp án
"Chia để trị", thực hiện văn hóa nô dịch, ngu dân là những chính sách của thực dân Pháp về chính trị và văn hóa, giáo dục nhằm nô dịch lâu dài nhân dân Việt Nam. Chọn C.
Câu 106:
Một nguyên nhân dẫn đến sự thất bại của phong trào yêu nước theo khuynh hướng dân chủ tư sản ở Việt Nam những năm đầu thế kỉ XX là gì?
 Xem đáp án
Xem đáp án
Hệ tư tưởng dân chủ tư sản cuối thế kỉ XIX, đầu thế kỉ XX mới xuất hiện tại Việt Nam, đây là một hệ tư tưởng mới với Việt Nam nhưng đã cũ với các quốc gia trên thế giới. Đồng thời giai cấp tư sản Việt Nam ra đời muộn, tiềm lực kinh tế nhỏ bé nên khả năng lãnh đạo còn hạn chế. Từ hai yếu tố đó cho thấy phong phong trào yêu nước theo khuynh hướng dân chủ tư sản thiếu sự lãnh đạo của một giai cấp tiên tiến. Chọn A.
Câu 107:
Sự phát triển kinh tế của Nhật Bản (1973-1991) thường xen kē với những giai đoạn suy thoái ngắn. Điều này chủ yếu là do
 Xem đáp án
Xem đáp án
Từ năm 1973, sự phát triển kinh tế của Nhật Bản thường xen kẽ với các đợt khủng hoảng, suy thoái ngắn do tác động của cuộc khủng hoảng năng lượng (1973). Chọn C.
Câu 108:
 Xem đáp án
Xem đáp án
Một trong những hạn chế của Luận cương chính trị của Đảng Cộng sản Đông Dương (10-1930) là đánh giá không đúng khả năng cách mạng của tầng lớp tiểu tư sản, giai cấp tư sản dân tộc, khả năng lôi kéo bộ phận trung, tiểu địa chủ tham gia Mặt trận dân tộc thống nhất, chống đế quốc và phong kiến. Chọn C.
Câu 109:
 Xem đáp án
Xem đáp án
Từ ngày 16 đến ngày 17-8-1945, Đại hội Quốc dân được triệu tập ở Tân Trào. Đại hội tán thành chủ trương Tổng khởi nghĩa của Đảng, thông qua 10 chính sách của Việt Minh, cử ra Uỷ ban Dân tộc giải phóng Việt Nam do Hồ Chí Minh làm Chủ tịch. Chọn D.
Câu 110:
 Xem đáp án
Xem đáp án
Theo nội dung của Hiệp định Sơ bộ thì: Chính phủ Pháp công nhận nước Việt Nam Dân chủ Cộng hoà là một quốc gia tự do, có chính phủ riêng, nghị viện riêng, quân đội riêng, tài chính riêng và là thành viên của Liên bang Đông Dương, nằm trong khối Liên hiệp Pháp. Chọn D.
Câu 111:
 Xem đáp án
Xem đáp án
Nhiệm vụ của cách mạng Việt Nam từ năm 1954 đến năm 1975 là: xây dựng chủ nghĩa xã hội ở miền Bắc, giải phóng miền Nam, thống nhất đất nước. Chọn B.
Câu 112:
 Xem đáp án
Xem đáp án
Câu 113:
 Xem đáp án
Xem đáp án
Câu 114:
 Xem đáp án
Xem đáp án
B loại, vì: đường biên giới dài gây khó khăn cho bảo vệ chủ quyền.
C loại, vì: phát triển nền kinh tế nhiều thành phần không liên quan nhiều đến yếu tố vị trí địa lý.
D loại, vì: phát triển nền nông nghiệp cận nhiệt đới → nền nông nghiệp nhiệt đới chứ không phải cận nhiệt.
Câu 115:
Vùng kinh tế nào ở nước ta có điều kiện tự nhiên thuận lợi nhất cho phát triển du lịch biển?
 Xem đáp án
Xem đáp án
Duyên hải Nam Trung Bộ với nhiều bãi biển đẹp, thời tiết thuận lợi quanh năm thuận lợi nhất cho phát triển du lịch biển. Chọn C.
Câu 116:
Căn cứ vào Atlat Địa lí Việt Nam trang 11, cho biết hai loại đất phổ biến của tỉnh Nam Định là
 Xem đáp án
Xem đáp án
Câu 117:
Cho biểu đồ:
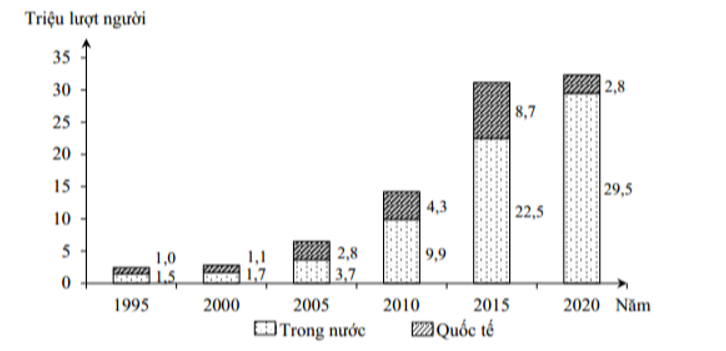
KHỐI LƯỢNG VẬN CHUYỂN HÀNH KHÁCH ĐƯỜNG HÀNG KHÔNG
PHÂN THEO HİNH THỨC QUA CÁC NĂM
(Nguồn: gso.gov.vn)
Theo biểu đồ, nhận xét nào sau đây không đúng về tình hình vận chuyển hành khách đường hàng không phân theo hình thức qua các năm?
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
- Đáp án A. Tổng khối lượng vận chuyển hành khách bằng đường hàng không tăng qua các năm → đúng.
- Đáp án B. Khối lượng vận chuyển khách trong nước luôn lớn hơn khách quốc tế → đúng.
- Đáp án C. Khối lượng vận chuyển khách quốc tế năm 2020 tăng so với năm 2015 → sai, năm 2020 khách quốc tế giảm. Chọn C.
- Đáp án D. Khối lượng vận chuyển khách trong nước năm 2020 gấp 19,7 lần năm 1995 → đúng.
Câu 118:
Dân cư nông thôn của nước ta có đặc điểm nào sau đây?
 Xem đáp án
Xem đáp án
Câu 119:
Để đạt trình độ hiện đại ngang tầm các nước tiên tiến trong khu vực, ngành bưu chính cần phát triển theo hướng
 Xem đáp án
Xem đáp án
Trong giai đoạn tới, ngành bưu chính sẽ phát triển theo hướng cơ giới hóa, tự động hóa, tin học hóa nhằm đạt trình độ hiện đại ngang tầm các nước tiên tiến trong khu vực. Chọn B.
Câu 120:
Tây Nguyên không phải là vùng
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
- Tây Nguyên giàu tài nguyên khoáng sản với trữ lượng lớn bô-xít và đá axít, asen → loại A
- Tây Nguyên được mệnh danh là kho vàng xanh của cả nước với diện tích rừng lớn → loại B
- Tây Nguyên có trữ năng thủy điện lớn thứ 2 cả nước → loại C
- Tây Nguyên nằm ở miền khí hậu phía Nam, không chịu ảnh hưởng của gió mùa đông bắc và không có mùa đông lạnh. Chọn D.
Câu 121:
Đồng bằng sông Cửu Long bị xâm nhập mặn nặng trong mùa khô là do
 Xem đáp án
Xem đáp án
Đồng bằng sông Cửu Long bị xâm nhập mặn nặng trong mủa khô là do địa hình thấp, ba mặt giáp biển, sông ngòi, kênh rạch chằng chịt.
A. nhiều cửa sông, ba mặt giáp biễn, có nhiều vùng trũng rộng lớn. → thiếu địa hình thấp.
B. địa hình thấp, ba mặt giáp biển, sông ngòi, kênh rạch chằng chịt. → đúng. Chọn B.
C. có nhiều vùng trũng rộng lớn, ba mặt giáp biển, địa hình đa dạng. → thiếu địa hình thấp.
D. sông ngòi, kênh rạch chằng chịt, ba mặt giáp biển, nhiều cửa sông. → thiếu địa hình thấp.
Câu 122:
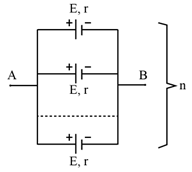
 Xem đáp án
Xem đáp án
Đoạn AB gồm n nguồn điện giống nhau ghép song song. Chọn A.
Câu 123:
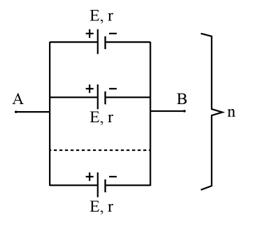
 Xem đáp án
Xem đáp án
Đoạn AB gồm n nguồn điện giống nhau ghép song song. Chọn A.
Câu 124:
Một tia sáng truyền trong không khí tới mặt thoáng của một chất lỏng. Tia phản xạ và tia khúc xạ vuông góc với nhau như hình vẽ. Trong các điều kiện đó, giữa các góc i và r có hệ thức nào?
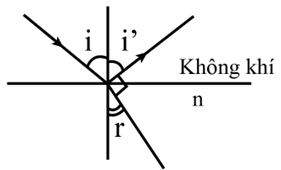
 Xem đáp án
Xem đáp án
Tia phản xạ và tia khúc xạ vuông góc với nhau nên ta có \({i^\prime } + r = 90^\circ \Rightarrow {\rm{i}} + {\rm{r}} = 90^\circ \) \( \Rightarrow {\rm{i}} = 90^\circ - {\rm{r}}\). Chọn B.
Câu 125:
Một tia sáng truyền trong không khí tới mặt thoáng của một chất lỏng. Tia phản xạ và tia khúc xạ vuông góc với nhau như hình vẽ. Trong các điều kiện đó, giữa các góc i và r có hệ thức nào?
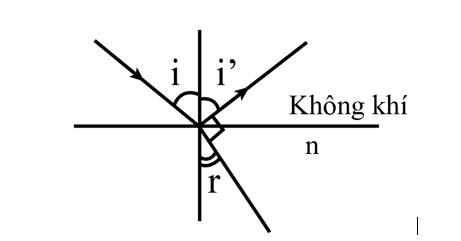
 Xem đáp án
Xem đáp án
Câu 126:
Hình vẽ nào dưới đây xác định không đúng hướng của vectơ cảm ứng từ tại M gây bởi dòng điện thẳng dài vô hạn?
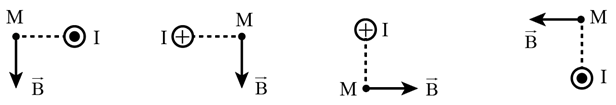
 Xem đáp án
Xem đáp án
Vận dụng quy tắc nắm tay phải ta xác định được các chiều của đường sức từ qua M: “Nắm bàn tay phải rồi đặt sao cho bốn ngón tay hướng theo chiều đường sức từ chạy qua dây dẫn thì ngón tay cái choãi ra chỉ chiều của dòng điện”. Chọn C.
Câu 127:

 Xem đáp án
Xem đáp án
Câu 128:
Cho một nguồn phát bức xạ điện từ chủ yếu (xem mỗi dụng cụ phát một bức xạ) gồm:
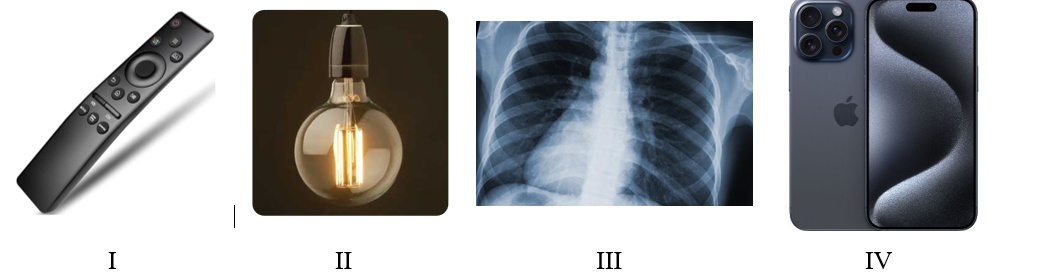
(I). Remote điều khiển từ xa.
(II). Đèn hơi thủy ngân.
(III). Máy chụp kiểm tra tổn thương xương ở cơ thể người.
(IV). Điện thoại di động.
Các bức xạ do các nguồn trên phát ra sắp xếp theo thứ tự tần số giảm dần là:
 Xem đáp án
Xem đáp án
Nguồn (I) phát ra tia hồng ngoại.
Nguồn (II) phát ra tia tử ngoại.
Nguồn (III) phát ra tia X.
Nguồn (IV) phát ra sóng vô tuyến.
Các bức xạ do các nguồn trên phát ra sắp xếp theo thứ tự tần số giảm dần là: (III), (II), (I), (IV). Chọn D.
Câu 129:
Cho một nguồn phát bức xạ điện từ chủ yếu (xem mỗi dụng cụ phát một bức xạ) gồm:
(I). Remote điều khiển từ xa.
(II). Đèn hơi thủy ngân.
(III). Máy chụp kiểm tra tổn thương xương ở cơ thể người.
(IV). Điện thoại di động.
Các bức xạ do các nguồn trên phát ra sắp xếp theo thứ tự tần số giảm dần là:
 Xem đáp án
Xem đáp án
Nguồn (I) phát ra tia hồng ngoại.
Nguồn (II) phát ra tia tử ngoại.
Nguồn (III) phát ra tia X.
Nguồn (IV) phát ra sóng vô tuyến.
Các bức xạ do các nguồn trên phát ra sắp xếp theo thứ tự tần số giảm dần là: (III), (II), (I), (IV). Chọn D.
Câu 130:
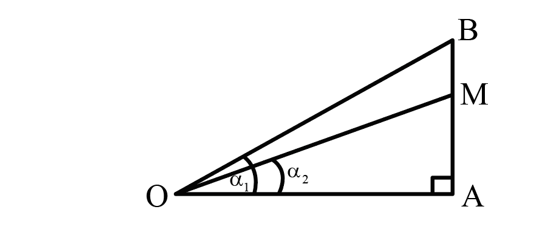
Tại điểm O đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm A cách O một đoạn x (m). Trên tia vuông góc với OA tại A lấy điểm B cách A một khoảng 5 m. Tại điểm M nằm trên đoạn AB sao cho AM = 3,2 m ta đặt một máy đo cường độ âm thanh. Thay đổi x để \[\widehat {MOB}\] có giá trị lớn nhất, khi đó mức cường độ âm tại A là LA = 35 dB. Coi các nguồn âm là hoàn toàn giống nhau. Để mức cường độ âm hiển thị trên máy đo là Lo = 45 dB thì cần đặt thêm tại O bao nhiêu nguồn âm nữa?
Đáp án: ……….
 Xem đáp án
Xem đáp án
Ta có OA = x (m); AB = 5 m; AM = 3,2 m.
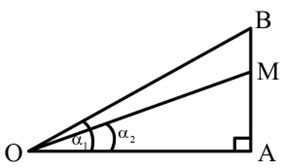
\(\tan \widehat {MOB} = \tan \left( {{{\rm{\alpha }}_1} - {{\rm{\alpha }}_2}} \right) = \frac{{\tan {{\rm{\alpha }}_1} - \tan {{\rm{\alpha }}_2}}}{{1 + \tan {{\rm{\alpha }}_1}\tan {{\rm{\alpha }}_2}}} = \frac{{\frac{5}{x} - \frac{{3,2}}{x}}}{{1 + \frac{5}{x}.\frac{{3,2}}{x}}} = \frac{{1,8}}{{x + \frac{{16}}{x}}}\)
Theo BĐT Cosi, ta có: \(x + \frac{{16}}{x} \ge 2\sqrt {16} = 8 \Rightarrow x = 8\,m.\) Do đó: \(OM = \sqrt {{8^2} + 3,{2^2}} = \frac{{8\sqrt {29} }}{5}m\)
Ta có: \({{\rm{L}}_{\rm{A}}} - {{\rm{L}}_{\rm{M}}} = 10\log \frac{{{{\rm{I}}_{\rm{A}}}}}{{{{\rm{I}}_M}}} \Leftrightarrow 35 - 45 = - 10 = 10\log \frac{{{{\rm{I}}_{\rm{A}}}}}{{{{\rm{I}}_{\rm{M}}}}} \Rightarrow \frac{{{{\rm{I}}_{\rm{A}}}}}{{{{\rm{I}}_{\rm{M}}}}} = 0,1\).
Ban đầu, tại O đặt 2 nguồn nên ta có: \({I_A} = \frac{{2P}}{{4\pi R_A^2}}\)
Gọi n là số nguồn cần đặt thêm tại O nên ta có: \({I_M} = \frac{{(n + 2)P}}{{4\pi R_M^2}}\)
\( \Rightarrow \frac{{{I_A}}}{{{I_M}}} = \frac{2}{{n + 2}}\frac{{R_M^2}}{{R_A^2}} \Rightarrow \frac{2}{{n + 2}}.\frac{{{{\left( {\frac{{8\sqrt {29} }}{5}} \right)}^2}}}{{{8^2}}} = 0,1 \Rightarrow n = 22.\)
Đáp án. 22.
Câu 131:
Cho một nguồn phát bức xạ điện từ chủ yếu (xem mỗi dụng cụ phát một bức xạ) gồm:

(I). Remote điều khiển từ xa.
(II). Đèn hơi thủy ngân.
(III). Máy chụp kiểm tra tổn thương xương ở cơ thể người.
(IV). Điện thoại di động.
Các bức xạ do các nguồn trên phát ra sắp xếp theo thứ tự tần số giảm dần là:
 Xem đáp án
Xem đáp án
Nguồn (I) phát ra tia hồng ngoại.
Nguồn (II) phát ra tia tử ngoại.
Nguồn (III) phát ra tia X.
Nguồn (IV) phát ra sóng vô tuyến.
Các bức xạ do các nguồn trên phát ra sắp xếp theo thứ tự tần số giảm dần là: (III), (II), (I), (IV). Chọn D.
Câu 132:
 Xem đáp án
Xem đáp án
Các phản ứng hạt nhân tuân theo các định luật: định luật bảo toàn điện tích, định luật bảo toàn động lượng, định luật bảo toàn năng lượng toàn phần. Chọn C.
Câu 133:
Tại điểm O đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm A cách O một đoạn x (m). Trên tia vuông góc với OA tại A lấy điểm B cách A một khoảng 5 m. Tại điểm M nằm trên đoạn AB sao cho AM = 3,2 m ta đặt một máy đo cường độ âm thanh. Thay đổi x để MOB có giá trị lớn nhất, khi đó mức cường độ âm tại A là LA = 35 dB. Coi các nguồn âm là hoàn toàn giống nhau. Để mức cường độ âm hiển thị trên máy đo là Lo = 45 dB thì cần đặt thêm tại O bao nhiêu nguồn âm nữa?
Đáp án: ……….
 Xem đáp án
Xem đáp án

Câu 134:
 Xem đáp án
Xem đáp án
Do \({\rm{i}} = \frac{{{\rm{\lambda D}}}}{{\rm{a}}}\), nghĩa là khoảng vân i tỉ lệ thuận với D.
Theo bài, khi dịch chuyển màn ra xa thì lúc đầu M là vân sáng sẽ chuyển thành vân tối nên ta có:
\(k\frac{{{\rm{\lambda }}D}}{a} = \left( {k - \frac{1}{2}} \right)\frac{{{\rm{\lambda }}{D^\prime }}}{a}\) \( \Rightarrow kD = \left( {k - \frac{1}{2}} \right)\left( {D + \frac{1}{7}} \right)\) \( \Rightarrow \frac{1}{7}k - \frac{1}{2}D = \frac{1}{{14}}\,\,\,\,\,\,\,\,(1)\)
\(k\frac{{{\rm{\lambda }}D}}{a} = \left( {k - \frac{1}{2} - 1} \right)\frac{{{\rm{\lambda }}{D^\prime }}}{a} \Rightarrow kD = \left( {k - \frac{3}{2}} \right)\left( {D + \frac{1}{7} + \frac{{16}}{{35}}} \right) \Rightarrow \frac{3}{5}k - \frac{3}{2}D = \frac{9}{{10}}\,\,\,\,\,\,\,\,\,(2)\)
Từ (1) và (2) ta có k = 4, D = 1 m. Chọn B.
Câu 135:
Các phản ứng hạt nhân không tuân theo định luật nào?
 Xem đáp án
Xem đáp án
Các phản ứng hạt nhân tuân theo các định luật: định luật bảo toàn điện tích, định luật bảo toàn động lượng, định luật bảo toàn năng lượng toàn phần. Chọn C.
Câu 136:
 Xem đáp án
Xem đáp án
Khi \({x_2} = 0,{x_1} = - 8\sqrt 3 \;{\rm{cm}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ - 8\sqrt 3 = 16\cos \left( {4{\rm{\pi }}t + \frac{{\rm{\pi }}}{{12}}} \right)}\\{0 = {A_2}\cos (4{\rm{\pi }}t + {\rm{\varphi }})}\end{array} \Rightarrow {\rm{\varphi }} = - \frac{{\rm{\pi }}}{4}} \right.\)
Khi \({x_1} = - 8\;{\rm{cm}}\)thì \({x_2} = 3,2\;{\rm{cm}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ - 8 = 16\cos \left( {4{\rm{\pi }}t + \frac{{\rm{\pi }}}{{12}}} \right)}\\{3,2 = {A_2}\cos \left( {4{\rm{\pi }}t - \frac{{\rm{\pi }}}{4}} \right)}\end{array} \Rightarrow {A_2} = 6,4\;{\rm{cm}}} \right.\)
Áp dụng số phức: \(x = {x_1} + {x_2} = 16\angle \frac{\pi }{{12}} + 6,4\angle - \frac{\pi }{4} \Rightarrow A \approx 20\;{\rm{cm}}{\rm{.}}\) Chọn B.
Câu 137:
Trong thí nghiệm giao thoa ánh sáng với khe Y-âng, xét điểm M trên màn, lúc đầu tại M là vân sáng, sau đó dịch màn ra xa mặt phẳng hai khe một đoạn nhỏ nhất là 1/7 m thì tại M là vân tối. Nếu tiếp tục dịch màn ra một đoạn nhỏ nhất 16/35m nữa thì tại M lại là vân tối. Khoảng cách giữa màn và mặt phẳng chứa hai khe là bao nhiêu?
 Xem đáp án
Xem đáp án
Do ![]() , nghĩa là khoảng vân i tỉ lệ thuận với D.
, nghĩa là khoảng vân i tỉ lệ thuận với D.
Theo bài, khi dịch chuyển màn ra xa thì lúc đầu M là vân sáng sẽ chuyển thành vân tối nên ta có:
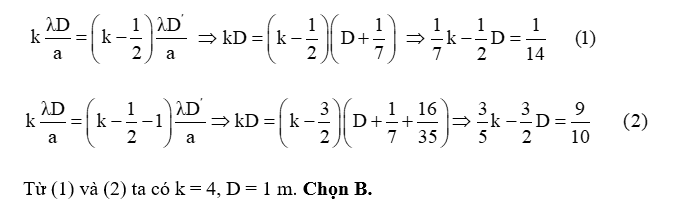
Câu 138:
 Xem đáp án
Xem đáp án
Thứ tự giảm dần về khả năng đâm xuyên của các tia phóng xạ là \({\rm{\gamma ,}}\,{\rm{\beta ,}}\,{\rm{\alpha }}\). Chọn C.
Câu 139:
Trong thí nghiệm giao thoa ánh sáng với khe Y-âng, xét điểm M trên màn, lúc đầu tại M là vân sáng, sau đó dịch màn ra xa mặt phẳng hai khe một đoạn nhỏ nhất là 1/7 m thì tại M là vân tối. Nếu tiếp tục dịch màn ra một đoạn nhỏ nhất 16/35m nữa thì tại M lại là vân tối. Khoảng cách giữa màn và mặt phẳng chứa hai khe là bao nhiêu?
 Xem đáp án
Xem đáp án
Do ![]() , nghĩa là khoảng vân i tỉ lệ thuận với D.
, nghĩa là khoảng vân i tỉ lệ thuận với D.
Theo bài, khi dịch chuyển màn ra xa thì lúc đầu M là vân sáng sẽ chuyển thành vân tối nên ta có:
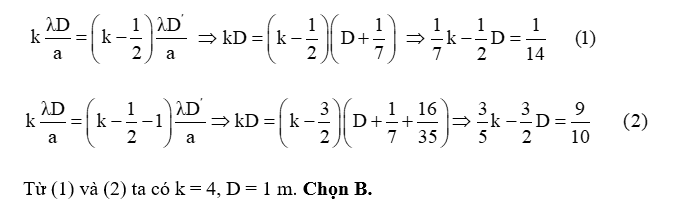
Câu 140:
 Xem đáp án
Xem đáp án
Nguyên tắc hoạt động của Pin năng lượng Mặt Trời dựa trên hiện tượng quang điện trong. Chọn B.
Câu 142:
Ở nhiều quốc gia trên thế giới, ethanol sinh ra từ quá trình lên men được trộn với xăng để góp phần bảo vệ môi trường. Nhiên liệu được quảng cáo dưới đây chứa \(85\% \) ethanol và \(15\% \) xăng về thể tích.

Ethanol thường được làm từ glucose, sử dụng men, trong điều kiện không có oxygen. Các enzyme trong đó sẽ xúc tác cho phản ứng này xảy ra:
Để sản xuất 1 lít loại nhiên liệu trên cần ít nhất bao nhiêu gam glucose? Biết khối lượng riêng của ethanol là \(0,8\;{\rm{g}}/{\rm{mL}}\).
 Xem đáp án
Xem đáp án
Ta có: 1 lít = 1000 mL nhiên liệu có chứa 85% ethanol về thể tích
Chọn A.
Câu 143:
Các bác sĩ chuyên ngành chẩn đoán hình ảnh cho biết phóng xạ có khả năng phá hủy cơ thể ở cấp độ tế bào và phân tử, làm hư hại phân tử ADN. Các tế bào có ADN bị hư hại sẽ chết đi hoặc diễn ra quá trình sửa chữa. Ở các cấp độ khác nhau, cơ thể chúng ta sẽ bị ảnh hưởng khác nhau. Hãy sắp xếp theo thứ tự giảm dần về khả năng đâm xuyên của các tia phóng xạ ![]() sau đây?
sau đây?
 Xem đáp án
Xem đáp án
Thứ tự giảm dần về khả năng đâm xuyên của các tia phóng xạ là ![]() . Chọn C.
. Chọn C.
Câu 144:
Copper sulfate ngậm nước hay còn gọi là đá xanh, có công thức hoá học là \({\rm{CuS}}{{\rm{O}}_4} \cdot {\rm{5}}{{\rm{H}}_2}{\rm{O}}\), thường được ứng dụng làm chất sát khuẩn, diệt nấm, diệt cỏ và thuốc trừ sâu,… Khi nung nóng, \({\rm{CuS}}{{\rm{O}}_4}.5{{\rm{H}}_2}{\rm{O}}\) mất dần khối lượng. Đồ thị biểu diễn độ giảm khối lượng của \({\rm{CuS}}{{\rm{O}}_4} \cdot 5{{\rm{H}}_2}{\rm{O}}\) khi tăng nhiệt độ nung như sau:
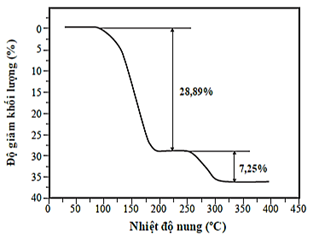
Thành phần gần nhất của chất rắn sau khi nhiệt độ đạt đến \({325^o}C\) là
 Xem đáp án
Xem đáp án
Khi nhiệt độ đạt đến \({325^o}C\) thì tổng độ giảm khối lượng là 28,89% + 7,25% = 36,14%.
Gọi công thức chất rắn khi đó là \({\rm{CuS}}{{\rm{O}}_4} \cdot {\rm{n}}{{\rm{H}}_2}{\rm{O}}\)
\(160 + 18n = 250 \cdot (100\% - 36,14\% )\)
\(n = 0\)
→ Thành phần gần nhất của chất rắn sau khi nhiệt độ đạt đến \({325^o}C\) là \(CuS{O_4}.\) Chọn C.
Câu 145:
Pin năng lượng mặt trời là thiết bị đặc biệt có khả năng chuyển đổi quang năng của ánh sáng mặt trời thành điện năng được lắp trong hệ thống điện Mặt Trời. Nó được cấu tạo từ các phần tử bán dẫn có chứa nhiều cảm biến ánh sáng điốt quang trên bề mặt, có hiệu suất cao và có tuổi thọ trung bình lên đến 30 năm. Nguyên tắc hoạt động của Pin năng lượng Mặt Trời dựa trên hiện tượng nào?
 Xem đáp án
Xem đáp án
Nguyên tắc hoạt động của Pin năng lượng Mặt Trời dựa trên hiện tượng quang điện trong. Chọn B.
Câu 146:
Một lọ đựng dung dịch \({\rm{AlC}}{{\rm{l}}_3}\) được xác định nồng độ như sau:
Thí nghiệm 1: Cho 15,0 mL dung dịch NaOH 1M vào cốc dung dịch chứa 10,0 mL dung dịch \({\rm{AlC}}{{\rm{l}}_3}\), sau phản ứng x gam kết tủa.
Thí nghiệm 2: Cho 27,0 mL dung dịch NaOH 1M vào dung dịch chứa 10,0 mL dung dịch \({\rm{AlC}}{{\rm{l}}_3},\)sau phản ứng cũng thu được x gam kết tủa.
Nồng độ của \({\rm{AlC}}{{\rm{l}}_3}\) là
 Xem đáp án
Xem đáp án
Thí nghiệm 1: Lượng \(O{H^ - }\) thêm vào chưa đủ để phản ứng hết với \[A{l^{3 + }}:\]
\[\begin{array}{l}A{l^{3 + }} + 3O{H^ - } \to Al{(OH)_3}\\\,\,\,\,\,\,\,\,\,\,\,\,0,015\,\,\, \to \,\,\,\,0,005\,\,\,\,\,\,\,\,\,\,\,\,(mol)\end{array}\]
Thí nghiệm 2: Lượng \(O{H^ - }\) thêm vào hòa tan một phần kết tủa:
Áp dụng công thức: \({n_{O{H^ - }}} = 4{n_{A{l^{3 + }}}} - {n_ \downarrow } \Rightarrow 0,027 = 4{n_{A{l^{3 + }}}} - 0,005 \Rightarrow {n_{A{l^{3 + }}}} = 0,008\,(mol)\)
Nồng độ của dung dịch \({\rm{AlC}}{{\rm{l}}_3}\) là \(0,8{\rm{M}}\)
Chọn D.
Câu 147:
Ở nhiều quốc gia trên thế giới, ethanol sinh ra từ quá trình lên men được trộn với xăng để góp phần bảo vệ môi trường. Nhiên liệu được quảng cáo dưới đây chứa 85% ethanol và 15% xăng về thể tích.

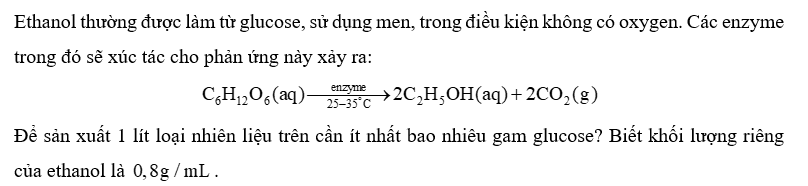
 Xem đáp án
Xem đáp án
Ta có: 1 lít = 1000 mL nhiên liệu có chứa 85% ethanol về thể tích
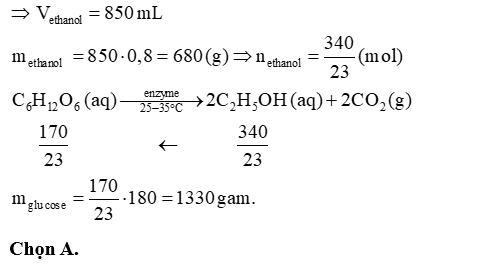
Câu 148:
 Xem đáp án
Xem đáp án
% số mol của \[{C_2}{H_5}OH\]trong X là \(50\% \to \frac{{\rm{x}}}{{{\rm{x}} + {\rm{y}} + {\rm{z}}}} \cdot 100\% = 50\% \,\,\,\,\,\,(3)\)
Từ (1), (2) và (3) \( \to \left\{ {\begin{array}{*{20}{l}}{x = 0,06}\\{y = 0,04}\\{z = 0,02}\end{array} \to {\rm{m}} = 0,06.46 + 0,04.74 + 0,02.44 = 6,6} \right.\) gam
- Khi cho 13,2 gam X (2m) tác dụng với \(AgN{O_3}/N{H_3}\)
Þ Trong 13,2 gam X có 0,04 mol \[C{H_3}CHO\]
Chọn B.
Câu 149:
![]()
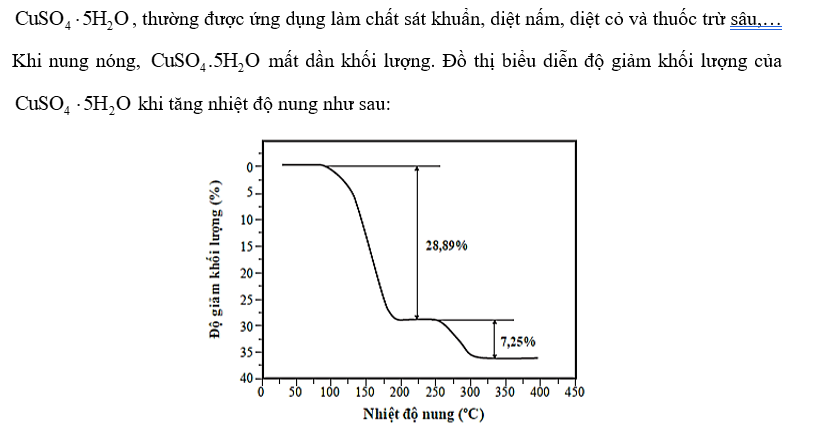
 Xem đáp án
Xem đáp án
Khi nhiệt độ đạt đến ![]() thì tổng độ giảm khối lượng là 28,89% + 7,25% = 36,14%.
thì tổng độ giảm khối lượng là 28,89% + 7,25% = 36,14%.
Gọi công thức chất rắn khi đó là ![]()

Câu 150:
Tiến hành phản ứng xà phòng hóa theo các bước sau:
Bước 1: Cho vào bát sứ: 1 gam mỡ lợn và 2,5 mL dung dịch NaOH 40%.
Bước 2: Đun hỗn hợp sôi nhẹ và liên tục khuấy đều bằng đũa thủy tinh (quá trình đun, có cho vào hỗn hợp vài giọt nước cất) trong thời gian 8 - 10 phút.
Bước 3: Rót thêm vào hỗn hợp 5 mL dung dịch NaCl bão hòa nóng, khuấy nhẹ, sau đó để nguội hỗn hợp.
Phát biểu nào sau đây không đúng?
 Xem đáp án
Xem đáp án
Mỡ lợn chứa các chất béo no như tristearin, tripanmitin, khi đun sôi với dung dịch NaOH xảy ra phản ứng xà phòng hóa (thủy phân chất béo):
.
Sản phẩm thu được gồm muối và glycerol dễ tan trong dung dịch nên sau bước 2 thu được chất lỏng đồng nhất.
Ở bước 3: để nguội và hòa tan thêm NaCl (muối ăn) vào \( \to \) làm giảm độ tan của muối sodium stearate, thêm nữa khối lượng riêng của dung dịch lúc này cũng tăng lên \( \to \) các muối hữu cơ (muối sodium của các acid béo) bị tách ra khỏi dung dịch, nhẹ hơn dung dịch dễ tách tạo chất rắn màu trắng nổi lên trên dung dịch. Do đó:
A. Đúng. Vì dầu nhớt thuộc loại alkane.
B. Đúng. Quan sát phương trình phản ứng trên thì việc thêm nước không phải là xúc tác của phản ứng. Thực chất việc nhỏ thêm vài giọt nước trong quá trình phản ứng là để giữ cho thể tích hỗn hợp không đổi.
C. Sai. Vì thêm dung dịch NaCl để tách muối sodium của các acid béo nổi lên trên.
D. Đúng. Sau bước 3, hỗn hợp tách thành hai lớp trong đó: phía trên là chất rắn màu trắng, phía dưới là chất lỏng.
Chọn C.
Câu 151:
 Xem đáp án
Xem đáp án
Polymer tổng hợp gồm: nylon-6; nylon-6,6; tơ nitron; cao su buna; poly(methyl methacrylate); PVC. Chọn B.
Câu 152:
 Xem đáp án
Xem đáp án
Đặt \({{\rm{n}}_{{\rm{AgN}}{{\rm{O}}_3}}} = {\rm{x}}\,{\rm{(mol)}},{{\rm{n}}_{{\rm{Fe}}{{\left( {{\rm{N}}{{\rm{O}}_3}} \right)}_2}}} = {\rm{y}}\,{\rm{(mol)}}.\)
Nhiệt phân hỗn hợp X thu được \({n_{{\rm{N}}{{\rm{O}}_2}}} = {\rm{x}} + 2{\rm{y}}\) mol;
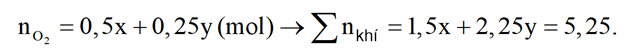
Để ý rằng nếu \({{\rm{O}}_2}\) thiếu thì \({\rm{N}}{{\rm{O}}_2}\) phản ứng với \({{\rm{H}}_2}{\rm{O}}\) tạo acid \({\rm{HN}}{{\rm{O}}_2}\) và \({\rm{HN}}{{\rm{O}}_3}\) do đó khí thoát ra là \({{\rm{O}}_2}\) dư
\(4N{O_2}\,\,\,\,\, + \,\,\,\,{O_2}\,\,\, + \,\,\,\,2{H_2}O \to 4HN{O_3}\)
Þ \({n_{{O_2}}}\)phản ứng =\(\frac{1}{4}{n_{N{O_2}}} = 0,25x + 0,5y\,(mol)\)
\( \Rightarrow {{\rm{n}}_{{O_2}}}\) dư = (0,5x + 0,25y) – (0,25x + 0,5y) = 0,25x – 0,25y = 0,25 (mol)
Giải hệ phương trình ta được:
\(\left\{ \begin{array}{l}x = 2\,(mol)\\y = 1\,(mol)\end{array} \right. \to {{\rm{m}}_{{\rm{AgN}}{{\rm{O}}_3}}} = 340\,{\rm{gam}},{{\rm{m}}_{{\rm{Fe}}{{\left( {{\rm{N}}{{\rm{O}}_3}} \right)}_2}}} = 180\,{\rm{gam}} \Rightarrow \% {\rm{Fe}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_2} = 34,62\% .\) Chọn A.
Câu 153:
Cho phản ứng hóa học: \({\rm{NaOH}} + {\rm{HCl}} \to {\rm{NaCl}} + {{\rm{H}}_2}{\rm{O}}.\)
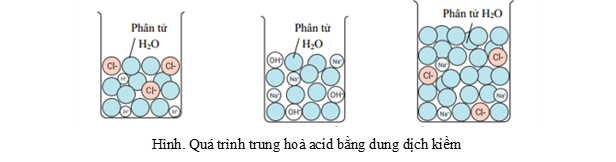
Phản ứng hóa học nào sau đây có cùng phương trình ion rút gọn với phản ứng trên?
 Xem đáp án
Xem đáp án
Quá trình trung hòa acid bằng dung dịch kiềm xảy ra phương trình ion rút gọn là \({{\rm{H}}^ + } + {\rm{O}}{{\rm{H}}^ - } \to {{\rm{H}}_2}{\rm{O}}\)
Phương trình ion rút gọn của từng phản ứng là
A. \(2{\rm{KOH}} + {\rm{FeC}}{{\rm{l}}_2} \to {\rm{Fe}}{({\rm{OH}})_2} + 2{\rm{KCl}} \Rightarrow {\rm{F}}{{\rm{e}}^{2 + }} + 2{\rm{O}}{{\rm{H}}^ - } \to {\rm{Fe}}{({\rm{OH}})_2}.\)
B. \(2{\rm{KOH}} + {{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4} \to {{\rm{K}}_2}{\rm{S}}{{\rm{O}}_4} + 2{{\rm{H}}_2}{\rm{O}}\) \( \Rightarrow {{\rm{H}}^ + } + {\rm{O}}{{\rm{H}}^ - } \to {{\rm{H}}_2}{\rm{O}}.\)
C. \({\rm{NaOH}} + {\rm{N}}{{\rm{H}}_4}{\rm{Cl}} \to {\rm{NaCl}} + {\rm{N}}{{\rm{H}}_3} + {{\rm{H}}_2}{\rm{O}} \Rightarrow {\rm{NH}}_4^ + + {\rm{O}}{{\rm{H}}^ - } \to {\rm{N}}{{\rm{H}}_3} + {{\rm{H}}_2}{\rm{O}}{\rm{.}}\)
D. \({\rm{NaOH}} + {\rm{NaHC}}{{\rm{O}}_3} \to {\rm{N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3} + {{\rm{H}}_2}{\rm{O}} \Rightarrow {\rm{HC}}{{\rm{O}}_3}^ - + {\rm{O}}{{\rm{H}}^ - } \to {\rm{CO}}_3^{2 - } + {{\rm{H}}_2}{\rm{O}}{\rm{.}}\)
Chọn B.
Câu 154:
Cho phản ứng sau ở trạng thái cân bằng:
Sự thay đổi nào sau đây làm cho cân bằng hoá học chuyển dịch về phía tạo ra sản phẩm?
 Xem đáp án
Xem đáp án
- Cân bằng hóa học dịch chuyển về phía tạo sản phẩm \( \to \) cân bằng chuyển dịch theo chiều thuận.
- Phản ứng thuận là phản ứng tỏa nhiệt nên khi tăng nhiệt độ cân bằng chuyển dịch về phía làm giảm nhiệt độ \((\Delta H > 0)\) \( \to \) loại A.
- Giảm thể tích bình chứa \( \to \) Áp suất trong bình tăng lên \( \to \) Cân bằng chuyển dịch theo chiều nghịch về phía làm giảm áp suất \( \to \) loại B.
- Chất xúc tác không làm cân bằng chuyển dịch \( \to \) loại C.
Chọn D.
Câu 155:
Hòa tan hết 14,3 gam hỗn hợp X gồm \({\rm{Al}}{\left( {{\rm{N}}{{\rm{O}}_3}} \right)_3},{\rm{MgO}},{\rm{Mg}}\)và \({\rm{Al}}\) vào dung dịch gồm 0,03 mol \({\rm{KN}}{{\rm{O}}_3}\) và \(0,5\,\;{\rm{mol}}\,{{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}\) (đun nóng). Sau khi kết thúc phản ứng thu được dung dịch Y chỉ chứa 59,85 gam muối và 3,584 lít (đktc) hỗn hợp khí Z gồm NO và \({{\rm{H}}_2}\)có tỉ khối so với \({{\rm{H}}_2}\) bằng 4,5. Dung dịch Y tác dụng tối đa với dung dịch chứa 1,11 mol KOH, lấy kết tủa nung ngoài không khí tới khối lượng không đổi thu được 10 gam rắn. Phần trăm khối lượng của Al có trong X là
Đáp án: ……….
 Xem đáp án
Xem đáp án
Xử lý nhanh các giả thiết số mol và tóm tắt thành sơ đồ sau:
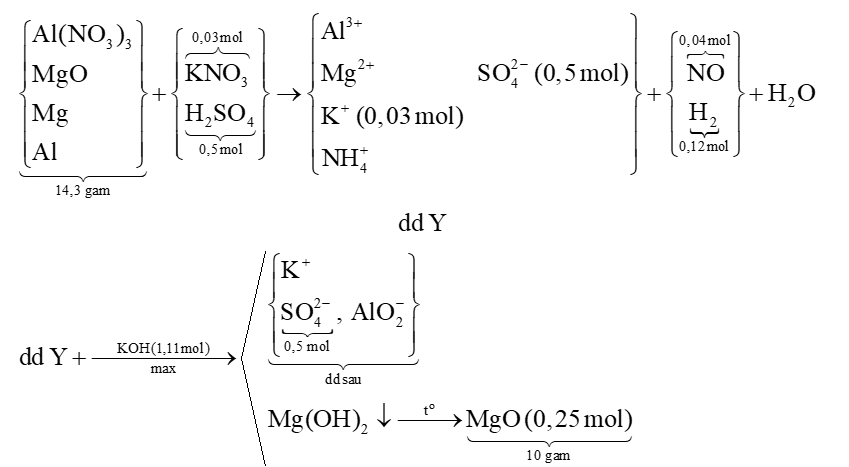
Bảo toàn khối lượng cả sơ đồ: \(14,3 + 0,03 \cdot 101 + 0,5 \cdot 98 = 59,85 + 0,16.9 + {m_{{H_2}O}}\)
→ \({{\rm{m}}_{{{\rm{H}}_2}{\rm{O}}}} = 5,04\) gam → \({n_{{H_2}O}} = 0,28\;{\rm{mol}}.\)
Bảo toàn nguyên tố \({\rm{H}}\)có:
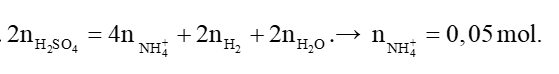
Trong dung dịch Y, bảo toàn điện tích ta có: \(3{n_{A{l^{3 + }}}} + 2 \cdot 0,25 + 1 \cdot 0,03 + 1 \cdot 0,05 = 2 \cdot 0,5\).
→ \({n_{A{l^{3 + }}}} = 0,14\,(mol)\)
Bảo toàn nguyên tố \({\rm{N}}\), ta có: \(3{n_{Al{{(N{O_3})}_3}}} + {n_{KN{O_3}}} = {n_{NO}} + {n_{NH_4^ + }}\).
→ \({{\rm{n}}_{{\rm{Al}}{{\left( {{\rm{N}}{{\rm{O}}_3}} \right)}_3}}} = 0,02\;{\rm{mol}} \Rightarrow {{\rm{n}}_{{\rm{Al trong X}}}} = 0,14 - 0,02 = 0,12\;{\rm{mol}}.\)
Vậy \(\% {m_{{\rm{Al trong X}}}} = \frac{{0,12 \cdot 27}}{{14,3}} \cdot 100\% \approx 22,66\% .\) Đáp án: 22,66%
Câu 156:
 Xem đáp án
Xem đáp án
Ở lá, hơi nước thoát chủ yếu qua con đường khí khổng. Chọn B.
Câu 157:
 Xem đáp án
Xem đáp án
A. Sai. pH máu người trung bình dao động từ 7,35 đến 7,45.
C. Sai. Khi cơ thể vận động mạnh, pH máu giảm.
D. Sai. Giảm nồng độ CO2 trong máu thì pH máu tăng.
Chọn B.
Câu 158:
 Xem đáp án
Xem đáp án
Cung phản xạ “co ngón tay của người” được mô tả theo sơ đồ sau:
Chọn C.
Câu 159:
 Xem đáp án
Xem đáp án
C. Sai. Enzim ARN pôlymeraza đóng vai trò tổng hợp đoạn mồi, vẫn trượt theo chiều 3’- 5’ đểtổng hợp đoạn mồi có chiều 5’ – 3’. Chọn C.
Câu 160:
 Xem đáp án
Xem đáp án
A. Sai. Vì đối với giống có kiểu gen đồng hợp (thuần chủng), khi tiến hành tự thụ phấn không gây ra thoái hóa giống. Chỉ có giống dị hợp mới dẫn tới thoái hóa giống.
B. Sai. Vì quá trình tự thụ phấn không làm thay đổi tần số alen của quần thể mà chỉ làm tăng tỉ lệ kiểu gen đồng hợp.
C. Đúng. Nguyên nhân là vì ở các quần thể tự thụ phấn thì tỉ lệ dị hợp giảm dần và sau nhiều thế hệ thì tỉ lệ dị hợp tiến tới = 0 nên quần thể chủ yếu chỉ gồm các dòng thuần chủng.
D. Sai. Vì quần thể giao phấn ngẫu nhiên có tính đa dạng di truyền cao hơn quần thể tự thụ phấn.
Chọn C.
Câu 161:
 Xem đáp án
Xem đáp án
Trong kĩ thuật chuyển gen, các nhà khoa học thường chọn thể truyền có gen đánh dấu để nhận biết các tế bào đã nhận được ADN tái tổ hợp. Chọn A.
Câu 162:
 Xem đáp án
Xem đáp án
\({\rm{P}}:({\rm{Aa}},{\rm{Bb}}) \times \frac{{ab}}{{ab}} \to \) Tỉ lệ kiểu hình thân thấp, hoa trắng ở đời con \( = \underline {ab} \times 1 = 38\% \) → Tỉ lệ giao tử \(\underline {ab} \) ở cây P dị hợp hai cặp gen \( = 0,38 > 0,25 \to \underline {ab} \) là giao tử liên kết.\( \to f = (0,5 - 0,38) \times 2 = 24\% \to \) Khoảng cách giữa 2 gen = tần số hoán vị gen \( = 24{\rm{cM}}\).
Chọn D.
Câu 163:
 Xem đáp án
Xem đáp án
B, D. Sai. Quần thể có kích thước nhỏ thường chịu tác động lớn của các nhân tố từ môi trường sống → nếu môi trường không đồng nhất và thường xuyên thay đổi thì khả năng thích nghi kém.
C. Sai. Quần thể sinh sản tự phối → độ đa dạng di truyền kém hơn quần thể ngẫu phối → nếu môi trường không đồng nhất và thường xuyên thay đổi thì khả năng thích nghi kém.
A. Đúng. Quần thể có kích thước lớn và sinh sản giao phối → quần thể có vô số biến dị tổ hợp → dù môi trường sống thường xuyên thay đổi thì quần thể vẫn có khả năng thích nghi được do tiềm ẩn sẵn kiểu gen thích nghi với môi trường mới. Chọn A.
Câu 164:
Một loài cá ép sống bám trên các loài cá lớn nhưng không ảnh hưởng đến sinh trưởng, phát triển, sinh sản của loài cá lớn. Loài cá ép sau khi bám lên cá lớn thì tạo nên các khe hở để 5 loài vi sinh vật khác bám lên và sinh sống nhưng không gây bệnh cho các loài tham gia. Có bao nhiêu phát biểu sau đây đúng?
I. Quan hệ giữa các cá ép với các loài vi sinh vật là quan hệ kí sinh.
II. Mối quan hệ giữa tất cả các loài nói trên đều là quan hệ hỗ trợ khác loài.
III. Quan hệ giữa vi sinh vật với cá lớn là quan hệ hội sinh.
IV. Nếu loài cá ép tách khỏi cá lớn thì các loài vi sinh vật cũng sẽ tách ra khỏi cá lớn.
 Xem đáp án
Xem đáp án
Có 3 phát biểu đúng, đó là II, III và IV.
I. Sai. Các loài vi sinh vật không sống trên cơ thể và cũng không gây hại cho cá ép nên đây không phải mối quan hệ kí sinh.
Chọn A.
Câu 165:
Ở một loài thực vật sinh sản bằng tự thụ phấn, gen A quy định khả năng nảy mầm trên đất có kim loại nặng, alen a không có khả năng này nên hạt có kiểu gen aa bị chết khi đất có kim loại nặng. Tiến hành gieo 1000 hạt (gồm 100 hạt AA, 400 hạt Aa, 500 hạt aa) trên đất có kim loại nặng các hạt sau khi nảy mầm đều sinh trưởng bình thường và các cây đều ra hoa, kết hạt tạo thế hệ F1; F1 nảy mầm và sinh trưởng, sau đó kết hạt tạo thế hệ F2. Lấy một hạt ở đời F2, xác suất để hạt nảy mầm được trên đất có kim loại nặng là bao nhiêu phần trăm?
Đáp án: ……….
 Xem đáp án
Xem đáp án
Ở thế hệ xuất phát, tỉ lệ kiểu gen ở cây trưởng thành là 0,2 AA : 0,8 Aa → Cho các cây trưởng thành ở thế hệ xuất phát tự thụ phấn (0,8 Aa tự thụ phấn sẽ sinh ra 3 loại kiểu gen là 0,2 AA : 0,4 AA : 0,2 aa; 0,2 AA tự thụ phấn sẽ sinh ra 0,2 AA) → Tỉ lệ hợp tử ở F1 là: 0,4 AA : 0,4 Aa : 0,2 aa.
- Vì hạt aa không nảy mầm được nên tỉ lệ kiểu gen ở cây trưởng thành F1 là: \(0,5AA:0,5Aa = \frac{1}{2}{\rm{AA}}:\frac{1}{2}{\rm{Aa}}\)→ Cho các cây trưởng thành ở thế hệ F1 tự thụ phấn → Tỉ lệ hợp tử ở F2 là: \(\frac{5}{8}{\rm{AA}}:\frac{1}{4}{\rm{Aa}}:\frac{1}{8}{\rm{aa}}\).
- Như vậy, ở F2 hạt nảy mầm gồm có \(\frac{5}{8}{\rm{AA}}\) và \(\frac{1}{4}{\rm{Aa}}\)→ Lấy ngẫu nhiên một hạt ở đời F2, xác suất để hạt này nảy mầm được trên đất có kim loại nặng là 5/8 + 1/4 = 87,5%. Đáp án: 87,5