ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Phương trình lượng giác cơ bản
-
1315 lượt thi
-
29 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Với giá trị nào của m dưới đây thì phương trình sinx = m có nghiệm?
 Xem đáp án
Xem đáp án
Phương trình sinx=m có nghiệm nếu\[\left| m \right| \le 1\]và vô nghiệm nếu\[\left| m \right| >1\]
Đáp án A:\[|m| = | - 3| = 3 >1\] =>Loại
Đáp án B: \[|m| = | - 2| = 2 >1\]=>Loại
Đáp án C: \[|m| = |0| = 0 \le 1\] =>Nhận
Đáp án D:\[|m| = |3| = 3 >1\] =>Loại
Đáp án cần chọn là: C
Câu 2:
Cho phương trình \[sinx = sin\alpha \]. Chọn kết luận đúng.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 3:
Chọn mệnh đề sai:
 Xem đáp án
Xem đáp án
Đáp án B: \[\sin x = 0 \Leftrightarrow x = k\pi \left( {k \in Z} \right)\] nên B đúng, C sai.
Đáp án D:\[\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \left( {k \in Z} \right)\] nên D đúng.
Đáp án cần chọn là: C
Câu 4:
Nghiệm của phương trình \[\sin x = \frac{1}{2}\] thỏa mãn \[ - \frac{\pi }{2} \le x \le \frac{\pi }{2}\] là:
 Xem đáp án
Xem đáp án
Bước 1:
Ta có:\[\sin x = \frac{1}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{6}\]
Bước 2:
\(\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \frac{{5\pi }}{6} + k2\pi }\end{array}} \right.(k \in Z)\)
Bước 3:
+) Xét\[x = \frac{\pi }{6} + k2\pi \]
Ta có\[ - \frac{\pi }{2} \le x \le \frac{\pi }{2} \Leftrightarrow - \frac{\pi }{2} \le \frac{\pi }{6} + k2\pi \le \frac{\pi }{2}\]
\[\begin{array}{*{20}{l}}{ - \frac{{2\pi }}{3} \le k2\pi \le \frac{\pi }{3} \Leftrightarrow - \frac{{2\pi }}{{3.2\pi }} \le k \le \frac{\pi }{{3.2\pi }}}\\{ \Leftrightarrow - \frac{1}{3} \le k \le \frac{1}{6}}\end{array}\]
Mà\[k \in \mathbb{Z} \Rightarrow k = 0\] Thay vào x ta được:\[x = \frac{\pi }{6}\]
+) Xét\[x = \frac{{5\pi }}{6} + k2\pi \]
\[\begin{array}{*{20}{l}}{ - \frac{\pi }{2} \le x \le \frac{\pi }{2} \Leftrightarrow - \frac{\pi }{2} \le \frac{{5\pi }}{6} + k2\pi \le \frac{\pi }{2}}\\{ \Leftrightarrow - \frac{{4\pi }}{3} \le k2\pi \le - \frac{\pi }{3} \Leftrightarrow - \frac{{4\pi }}{{3.2\pi }} \le k \le - \frac{\pi }{{3.2\pi }}}\\{ \Leftrightarrow - \frac{2}{3} \le k \le - \frac{1}{6}}\end{array}\]
Mà\[k \in \mathbb{Z}\] nên không có giá trị k thỏa mãn
Vậy phương trình ban đầu có nghiệm duy nhất là\[x = \frac{\pi }{6}\]
Đáp án cần chọn là: B
Câu 5:
Số nghiệm của phương trình \[2\sin \left( {x + \frac{\pi }{4}} \right) - 2 = 0\]với \[\pi \le x \le 5\pi \]là:
 Xem đáp án
Xem đáp án
Ta có:
\[2\sin \left( {x + \frac{\pi }{4}} \right) - 2 = 0 \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = 1 \Leftrightarrow x + \frac{\pi }{4} = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{4} + k2\pi \left( {k \in Z} \right)\]
Mà
\[\pi \le x \le 5\pi \Rightarrow \pi \le \frac{\pi }{4} + k2\pi \le 5\pi \Leftrightarrow \frac{{3\pi }}{4} \le k2\pi \le \frac{{19\pi }}{4} \Leftrightarrow \frac{3}{8} \le k \le \frac{{19}}{8} \Rightarrow k \in \left\{ {1;2} \right\}\]
Vậy phương trình có hai nghiệm trong đoạn \[\left[ {\pi ;5\pi } \right]\]Đáp án cần chọn là: D
Câu 6:
Nghiệm của phương trình \[\sin x.\cos x = 0\] là:
 Xem đáp án
Xem đáp án
Bước 1:
\[\sin x.\cos x = 0 \Leftrightarrow \frac{1}{2}\sin 2x = 0\]
Bước 2:
\[\Leftrightarrow \sin 2x = 0 \Leftrightarrow 2x = k\pi \Leftrightarrow x = \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: B
Câu 7:
Phương trình \[\cos 2x = 1\] có nghiệm là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 8:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Ta có:
+)\[\cos x \ne 1 \Leftrightarrow x \ne k2\pi \left( {k \in Z} \right)\] nên A sai.
+)\[\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \left( {k \in Z} \right)\] nên B đúng, D sai.
+) \[\cos x \ne - 1 \Leftrightarrow x \ne \pi + k2\pi \left( {k \in Z} \right)\] nên C sai.
Đáp án cần chọn là: B
Câu 9:
Nghiệm của phương trình \[2\cos x - 1 = 0\] là:
 Xem đáp án
Xem đáp án
Ta có:
\[2\cos x - 1 = 0 \Leftrightarrow \cos x = \frac{1}{2} \Leftrightarrow \cos x = \cos \frac{\pi }{3} \Leftrightarrow x = \pm \frac{\pi }{3} + k2\pi \left( {k \in Z} \right)\]
Đáp án cần chọn là: D
Câu 10:
Số nghiệm của phương trình \[\sqrt 2 \cos \left( {x + \frac{\pi }{3}} \right) = 1\]với \[0 \le x \le 2\pi \;\]là:
 Xem đáp án
Xem đáp án
Ta có:\[\sqrt 2 \cos \left( {x + \frac{\pi }{3}} \right) = 1 \Leftrightarrow \cos \left( {x + \frac{\pi }{3}} \right) = \frac{1}{{\sqrt 2 }} = \cos \frac{\pi }{4}\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + \frac{\pi }{3} = \frac{\pi }{4} + k2\pi }\\{x + \frac{\pi }{3} = - \frac{\pi }{4} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{{12}} + k2\pi }\\{x = - \frac{{7\pi }}{{12}} + k2\pi }\end{array}} \right.(k \in Z)\)
Vì \[0 \le x \le 2\pi \]nên\[0 \le - \frac{\pi }{{12}} + k2\pi \le 2\pi \Leftrightarrow \frac{\pi }{{12}} \le k2\pi \le \frac{{25\pi }}{{12}} \Leftrightarrow \frac{1}{{24}} \le k \le \frac{{25}}{{24}} \Rightarrow k = 1\]
Và \[0 \le - \frac{{7\pi }}{{12}} + k2\pi \le 2\pi \Leftrightarrow \frac{{7\pi }}{{12}} \le k2\pi \le \frac{{31\pi }}{{12}} \Leftrightarrow \frac{7}{{24}} \le k \le \frac{{31}}{{24}} \Rightarrow k = 1\]
Vậy có hai nghiệm của phương trình trong khoảng \[\left[ {0;2\pi } \right]\]Đáp án cần chọn là: B
Câu 11:
Nghiệm của phương trình \[\cos 3x = \cos x\] là:
 Xem đáp án
Xem đáp án
Bước 1:
Ta có:
\[cos3x = cosx \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = x + k2\pi }\\{3x = - x + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = k2\pi }\\{4x = k2\pi }\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{x = \frac{{k\pi }}{2}}\end{array}} \right.} \right.\]
Bước 2:
+) Với họ nghiệm \[x = k\pi \] ta có:
Khi k=0 thì x=0, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k chẵn)
Khi k=1 thì \[x = \pi \], điểm biểu diễn là A' (Vẫn là điểm đó khi k lẻ).
Như thế họ nghiệm \[x = k\pi \] có 2 điểm biểu diễn là A,A′.
+) Với họ nghiệm\[x = \frac{{k\pi }}{2}\] ta có:
Khi k=0 thì x=0, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k có dạng 4m, tức là k chia hết cho 4)
Khi k=1 thì \[x = \frac{\pi }{2}\] điểm biểu diễn là B (Vẫn là điểm đó khi k có dạng 4m+1).
Khi k=2 thì \[x = \pi \] điểm biểu diễn là A' (Vẫn là điểm đó khi k có dạng 4m+2).
Khi k=3 thì\[x = \frac{{3\pi }}{2}\] điểm biểu diễn là B' (Vẫn là điểm đó khi k có dạng 4m+3).
Như thế họ nghiệm\[x = \frac{{k\pi }}{2}\] có 44 điểm biểu diễn là A,A′,B,B′.
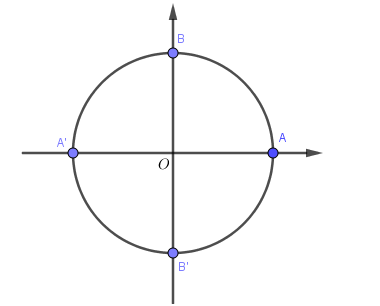
+) Kết hợp các điểm này lại ta được tổng cộng vẫn là 4 điểm A,A′,B,B′. Mà 4 điểm này là 4 điểm biểu diễn của chính họ nghiệm\[x = \frac{{k\pi }}{2}\] nên nghiệm của phương trình ban đầu là \[x = \frac{{k\pi }}{2}k \in Z\]
Đáp án cần chọn là: C
Câu 12:
Nghiệm của phương trình \[{\sin ^2}x - \sin x = 0\] thỏa điều kiện: \[0 < x < \pi .\]
 Xem đáp án
Xem đáp án
Bước 1:
\[si{n^2}x - sinx = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sinx = 0}\\{sinx = 1}\end{array}} \right.\]
Bước 2:
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{x = \frac{\pi }{2} + k2\pi }\end{array}} \right.(k \in \mathbb{Z})\)
Bước 3:
Xét\[x = k\pi ,k \in \mathbb{Z}\]
Vì\[0 < x < \pi \] nên nghiệm của phương trình thỏa mãn:
\[0 < k\pi < \pi \Leftrightarrow 0 < k < 1\]
Ta không thể tìm được số nguyên nào thỏa mãn điều trên
=>Không có số k trong trường hợp này.
Xét\[x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\]
Vì\[0 < x < \pi \]nên nghiệm của phương trình thỏa mãn:
\[0 < \frac{\pi }{2} + k2\pi < \pi \Leftrightarrow - \frac{\pi }{2} < k2\pi < \frac{\pi }{2}\]
\[ \Leftrightarrow - \frac{1}{4} < k < \frac{1}{4}\]mà\[k \in \mathbb{Z} \Rightarrow k = 0\]Thay vào x ta được:
\[x = \frac{\pi }{2} + 0 = \frac{\pi }{2}\]
Vậy phương trình có 1 nghiệm duy nhất là \[x = \frac{\pi }{2}\]
Đáp án cần chọn là: A
Câu 13:
Nghiệm của phương trình \[\sin 3x = \cos x\] là:
 Xem đáp án
Xem đáp án
Ta có:
\[\sin 3x = \cos x \Leftrightarrow \sin 3x = \sin \left( {\frac{\pi }{2} - x} \right)\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = (\frac{\pi }{2} - x) + k2\pi }\\{3x = \pi - (\frac{\pi }{2} - x) + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = \frac{\pi }{2} + k2\pi }\\{2x = \frac{\pi }{2} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{8} + \frac{{k\pi }}{2}}\\{x = \frac{\pi }{4} + k\pi }\end{array}} \right.(k \in Z)\)
Đáp án cần chọn là: A
Câu 14:
Nghiệm của phương trình \[\sqrt 3 \tan x + 3 = 0\] là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 15:
Phương trình \[\tan \frac{x}{2} = \tan x\] có nghiệm:
 Xem đáp án
Xem đáp án
Bước 1:
Điều kiện:\(\left\{ {\begin{array}{*{20}{c}}{cosx \ne 0}\\{cos\frac{x}{2} \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne \frac{\pi }{2} + k\pi }\\{\frac{x}{2} \ne \frac{\pi }{2} + k\pi }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne \frac{\pi }{2} + k\pi }\\{x \ne \pi + k2\pi }\end{array}} \right.\)
Bước 2:
Ta có: \[\tan \frac{x}{2} = \tan x \Leftrightarrow \frac{x}{2} = x + k\pi \Leftrightarrow - \frac{x}{2} = k\pi \Leftrightarrow - x = 2k\pi \]
\[ \Leftrightarrow x = - k2\pi \left( {k \in Z} \right)\]Đặt k = −l nên:\[ \Leftrightarrow x = l2\pi \left( {l \in Z} \right)\] (TMĐK)
Đáp án cần chọn là: A
Câu 16:
Phương trình \[\sqrt 3 \cot \left( {5x - \frac{\pi }{8}} \right) = 0\]có nghiệm là:
 Xem đáp án
Xem đáp án
ĐKXĐ: \[\sin \left( {5x - \frac{\pi }{8}} \right) \ne 0 \Leftrightarrow 5x - \frac{\pi }{8} \ne k\pi \Leftrightarrow x \ne \frac{\pi }{{40}} + \frac{{k\pi }}{5}\left( {k \in Z} \right)\]
Ta có:
\[\sqrt 3 \cot \left( {5x - \frac{\pi }{8}} \right) = 0 \Leftrightarrow \cot \left( {5x - \frac{\pi }{8}} \right) = 0 \Leftrightarrow 5x - \frac{\pi }{8} = \frac{\pi }{2} + k\pi \]
\[ \Leftrightarrow 5x = \frac{{5\pi }}{8} + k\pi \Leftrightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{5}\left( {k \in Z} \right)\]
Đáp án cần chọn là: B
Câu 17:
Tập nghiệm của phương trình \[\tan x.\cot x = 1\] là:
 Xem đáp án
Xem đáp án
Điều kiện xác định:
\(\left\{ {\begin{array}{*{20}{c}}{cosx \ne 0}\\{sinx \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne \frac{\pi }{2} + k\pi }\\{x \ne k\pi }\end{array}} \right. \Leftrightarrow x \ne \frac{{k\pi }}{2} \Rightarrow D = R \setminus \{ \frac{{k\pi }}{2},k \in Z\} \)
Do\[\tan x.\cot x = 1,\forall x \in D\]nên tập nghiệm của phương trình là \[R \setminus \left\{ {\frac{{k\pi }}{2},k \in Z} \right\}\]
Đáp án cần chọn là: A
Câu 18:
Phương trình \[\tan \left( {\frac{\pi }{2} - x} \right) + 2\tan \left( {2x + \frac{\pi }{2}} \right) = 1\] có nghiệm là:
 Xem đáp án
Xem đáp án
Bước 1:
Ta có: \[\tan \left( {\frac{\pi }{2} - x} \right) + 2\tan \left( {2x + \frac{\pi }{2}} \right) = 1 \Leftrightarrow \cot x - 2\cot 2x = 1\]
ĐK: \(\left\{ {\begin{array}{*{20}{c}}{sinx \ne 0}\\{sin2x \ne 0}\end{array}} \right. \Leftrightarrow sin2x \ne 0 \Leftrightarrow x \ne \frac{{k\pi }}{2}\)
Bước 2:
Khi đó phương trình tương đương:
\[\begin{array}{*{20}{l}}{\cot x - 2\cot 2x = 1}\\{ \Leftrightarrow \cot x - 2.\frac{{1 - {{\tan }^2}x}}{{2\tan x}} = 1}\\{ \Leftrightarrow \cot x - \frac{{\tan x.\cot x - {{\tan }^2}x}}{{\tan x}} = 1}\\{ \Leftrightarrow \cot x - \left( {\cot x - \tan x} \right) = 1 \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \left( {k \in Z} \right)\left( {TMDK} \right)}\end{array}\]
Đáp án cần chọn là: B
Câu 19:
Phương trình \[\cos 11x\cos 3x = \cos 17x\cos 9x\] có nghiệm là:
 Xem đáp án
Xem đáp án
Bước 1:
\[\cos 11x\cos 3x = \cos 17x\cos 9x\]
\[ \Leftrightarrow \frac{1}{2}.\left[ {\cos \left( {11x + 3x} \right) + \cos \left( {11x - 3x} \right)} \right] = \frac{1}{2}\left[ {\cos \left( {17x + 9x} \right) + \cos \left( {17x - 9x} \right)} \right]\]
\[\begin{array}{l} \Leftrightarrow \frac{1}{2}\left( {\cos 14x + \cos 8x} \right) = \frac{1}{2}\left( {\cos 26x + \cos 8x} \right)\\ \Leftrightarrow \cos 14x + \cos 8x = \cos 26x + \cos 8x\\ \Leftrightarrow \cos 14x = \cos 26x\end{array}\]
Bước 2:
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{12x = k2\pi }\\{40x = k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{k\pi }}{6}}\\{x = \frac{{k\pi }}{{20}}}\end{array}} \right.(k \in \mathbb{Z})\)
Vậy nghiệm của phương trình là\[x = \frac{{k\pi }}{6},\,\,x = \frac{{k\pi }}{{20}}\]
Vậy nghiệm của phương trình là\[x = \frac{{k\pi }}{6},\,\,x = \frac{{k\pi }}{{20}}\]
Đáp án cần chọn là: B
Câu 20:
Nghiệm của phương trình \[\tan \left( {2x - {{15}^0}} \right) = 1\], với \[ - {90^0} < x < {90^0}\;\]là:
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{*{20}{l}}{\tan \left( {2x - {{15}^0}} \right) = 1 = \tan {{45}^0}}\\{ \Leftrightarrow 2x - {{15}^0} = {{45}^0} + k{{180}^0}}\\{ \Leftrightarrow 2x = {{60}^0} + k{{180}^0}}\\{ \Leftrightarrow x = {{30}^0} + k{{90}^0}}\end{array}\]
Theo bài ra ta có:
\[\begin{array}{l} - {90^0} < x < {90^0}\\ \Leftrightarrow - {90^0} < {30^0} + k{90^0} < {90^0}\\ \Leftrightarrow - {120^0} < k{90^0} < {60^0}\\ \Leftrightarrow - \frac{4}{3} < k < \frac{2}{3}\end{array}\]
Mà \[k \in \mathbb{Z} \Rightarrow k \in \left\{ {0; - 1} \right\}\]
Với k=0 ta có nghiệm\[x = {30^0}\]
Với k=−1 ta có nghiệm\[x = {30^0} - {90^0} = - {60^0}\]
Vậy phương trình đã cho có 2 nghiệm thỏa mãn là\[x = - {60^0},\,\,x = {30^0}\]
Đáp án cần chọn là: D
Câu 21:
Phương trình \[\cot 20x = 1\] có bao nhiêu nghiệm thuộc khoảng \[\left[ { - 50\pi ;0} \right]?\]
 Xem đáp án
Xem đáp án
Ta có: \[\cot 20x = 1 \Leftrightarrow 20x = \frac{\pi }{4} + k\pi \Leftrightarrow x = \frac{\pi }{{80}} + \frac{{k\pi }}{{20}}\,\,\left( {k \in \mathbb{Z}} \right)\]
Theo bài ra ta có:
\[\begin{array}{*{20}{l}}{x \in \left[ { - 50\pi ;0} \right]}\\{ \Leftrightarrow - 50\pi \le \frac{\pi }{{80}} + \frac{{k\pi }}{{20}} \le 0}\\{ \Leftrightarrow - 50 \le \frac{1}{{80}} + \frac{k}{{20}} \le 0}\\{ \Leftrightarrow - \frac{{4001}}{4} \le k \le - \frac{1}{4}}\\{ \Leftrightarrow - 1000,25 \le k \le - 0,25}\end{array}\]
Mà\[k \in \mathbb{Z} \Rightarrow - 1000 \le k \le - 1\]
\[ \Rightarrow k \in \left\{ { - 1000; - 999;....; - 2; - 1} \right\}\]
Tập trên có \[ - 1 - ( - 1000) + 1 = 1000\]phần tử suy ra có 1000 giá trị nguyên của kk thỏa mãn.
Vậy phương trình đã cho có 1000 nghiệm thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: D
Câu 22:
Nghiệm của phương trình \[\cot x = \cot 2x\] là :
 Xem đáp án
Xem đáp án
ĐK: \(\left\{ {\begin{array}{*{20}{c}}{sinx \ne 0}\\{sin2x \ne 0}\end{array}} \right. \Leftrightarrow sin2x \ne 0 \Leftrightarrow 2x \ne k\pi \Leftrightarrow x \ne \frac{{k\pi }}{2}(k \in Z)\)
\[\cot x = \cot 2x \Leftrightarrow 2x = x + k\pi \Leftrightarrow x = k\pi \,\,\left( {k \in Z} \right)\,\,\,\left( {ktm} \right)\]
Vậy phương trình đã cho vô nghiệm.
Đáp án cần chọn là: D
Câu 23:
Tìm tập xác định D của hàm số sau \[y = \frac{{2\sin x - 1}}{{\tan 2x + \sqrt 3 }}\].
 Xem đáp án
Xem đáp án
Hàm số\[y = \frac{{2\sin x - 1}}{{\tan 2x + \sqrt 3 }}\]xác định khi
\(\left\{ {\begin{array}{*{20}{c}}{cos2x \ne 0}\\{tan2x \ne - \sqrt 3 }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x \ne \frac{\pi }{2} + k\pi }\\{2x \ne - \frac{\pi }{3} + k\pi }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne \frac{\pi }{4} + \frac{{k\pi }}{2}}\\{x \ne - \frac{\pi }{6} + k\frac{\pi }{2}}\end{array}} \right.(k \in \mathbb{Z})\)
Đáp án cần chọn là: D
Câu 24:
Số nghiệm của phương trình \[\cos 2x = \frac{1}{2}\] trên nửa khoảng \[({0^0};{36^0}]\;\]là?
 Xem đáp án
Xem đáp án
Ta có:
\[cos2x = \frac{1}{2} \Leftrightarrow cos2x = cos\frac{\pi }{3} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \frac{\pi }{3} + k2\pi }\\{2x = - \frac{\pi }{3} + k2\pi }\end{array}} \right. \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi \,\,(k \in \mathbb{Z})\]
Trên nửa khoảng \[\left( {{0^0};{{360}^0}} \right]\]tức\[\left( {0;2\pi } \right]\] Ta sẽ có các nghiệm thỏa mãn như sau:
\[ + )\,\,\,0 < x = \frac{\pi }{6} + k\pi \le 2\pi \Leftrightarrow - \frac{1}{6} < k \le \frac{{11}}{6}\]mà \[k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1} \right\}\]Có 2 nghiệm.
\[ + )\,\,\,0 < x = - \frac{\pi }{6} + k\pi \le 2\pi \Leftrightarrow \frac{1}{6} < k \le \frac{{13}}{6}\]mà\[k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2} \right\}\]Có 2 nghiệm.
Vậy có 4 nghiệm thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: D
Câu 25:
Phương trình \[\cos 3x = 2{m^2} - 3m + 1\]. Xác định mm để phương trình có nghiệm \[x \in (0;\frac{\pi }{6}]\]
 Xem đáp án
Xem đáp án
Bước 1:
Với \[x \in \left( {0;\frac{\pi }{6}} \right] \Rightarrow 3x \in \left( {0;\frac{\pi }{2}} \right]\]
Hàm số\[y = \cos x\] nghịch biến trên\[\left( {0;\frac{\pi }{2}} \right)\] nên ta có:
\[0 < 3x \le \frac{\pi }{2} \Leftrightarrow \cos \frac{\pi }{2} \le \cos 3x \le \cos 0 \Leftrightarrow 0 \le \cos 3x < 1\]
Bước 2:
Do đó phương trình\[\cos 3x = 2{m^2} - 3m + 1\] có nghiệm khi và chỉ khi:\[0 \le 2{m^2} - 3m + 1 < 1\]
\(\left\{ {\begin{array}{*{20}{c}}{2{m^2} - 3m + 1 \ge 0}\\{2{m^2} - 3m + 1 < 1}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{m \ge 1}\\{m \le \frac{1}{2}}\end{array}} \right.}\\{0 < m < \frac{3}{2}}\end{array}} \right.\)
Kết hợp nghiệm:
\[ \Leftrightarrow m \in \left( {0;\frac{1}{2}} \right] \cup \left[ {1;\frac{3}{2}} \right)\]
Đáp án cần chọn là: C
Câu 26:
Cho phương trình \[\sin \left( {2x - \frac{\pi }{5}} \right) = 3{m^2} + \frac{m}{2}\]. Biết \(x = \frac{{11\pi }}{{60}}\) là một nghiệm của phương trình. Tính m.
 Xem đáp án
Xem đáp án
Thay\[x = \frac{{11\pi }}{{60}}\] vào phương trình ta có:
\[sin(2.\frac{{11\pi }}{{60}} - \frac{\pi }{5}) = 3{m^2} + \frac{m}{2} \Leftrightarrow sin\frac{\pi }{6} = 3{m^2} + \frac{m}{2}\]
\[ \Leftrightarrow \frac{1}{2} = 3{m^2} + \frac{m}{2} \Leftrightarrow 6{m^2} + m = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = \frac{1}{3}}\\{m = - \frac{1}{2}}\end{array}} \right.\]
Đáp án cần chọn là: D
Câu 27:
Phương trình lượng giác \[\frac{{\cos x - \frac{{\sqrt 3 }}{2}}}{{\sin x - \frac{1}{2}}} = 0\] có nghiệm là:
 Xem đáp án
Xem đáp án
ĐKXĐ:\[sinx - \frac{1}{2} \ne 0 \Rightarrow sinx \ne \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \ne \frac{\pi }{6} + k2\pi }\\{x \ne \frac{{5\pi }}{6} + k2\pi }\end{array}} \right.(k \in \mathbb{Z})\]
\(\frac{{cosx - \frac{{\sqrt 3 }}{2}}}{{sinx - \frac{1}{2}}} = 0 \Leftrightarrow cosx - \frac{{\sqrt 3 }}{2} \Leftrightarrow cosx = \frac{{\sqrt 3 }}{2}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = - \frac{\pi }{6} + k2\pi }\end{array}} \right.(k \in \mathbb{Z})\)
Đối chiếu ĐKXĐ ta thấy chỉ có nghiệm\[x = - \frac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\] thỏa mãn.
Vậy nghiệm của phương trình là\[x = - \frac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: C
Câu 28:
Phương trình \[\sin \left( {2x + \frac{\pi }{7}} \right) = {m^2} - 3m + 3\] vô nghiệm khi:
 Xem đáp án
Xem đáp án
Phương trình\[\sin \left( {2x + \frac{\pi }{7}} \right) = {m^2} - 3m + 3\] vô nghiệm khi và chỉ khi:
\(\left[ {\begin{array}{*{20}{c}}{{m^2} - 3m + 3 >1}\\{{m^2} - 3m + 3 < - 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{m^2} - 3m + 2 >0}\\{{m^2} - 3m + 4 < 0(vo\,\,nghiem)}\end{array}} \right.} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m >2}\\{m < 1}\end{array}} \right.\)
Đáp án cần chọn là: C
Câu 29:
Giải phương trình lượng giác \[\sin \left( {\frac{\pi }{3} - 3x} \right) = \sin \left( {x + \frac{\pi }{4}} \right)\] có nghiệm là:
 Xem đáp án
Xem đáp án
\[sin(\frac{\pi }{3} - 3x) = sin(x + \frac{\pi }{4})\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{\pi }{3} - 3x = x + \frac{\pi }{4} + k2\pi }\\{\frac{\pi }{3} - 3x = \pi - x - \frac{\pi }{4} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 4x = - \frac{\pi }{{12}} + k2\pi }\\{ - 2x = \frac{{5\pi }}{{12}} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{48}} + \frac{{k\pi }}{2}}\\{x = \frac{{ - 5\pi }}{{24}} + k\pi }\end{array}} \right.(k \in \mathbb{Z})\)
Đáp án cần chọn là: A
