Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 29)
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 29)
-
93 lượt thi
-
149 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Dịch bệnh Viêm đường hô hấp cấp Covid-19. Tính đến 9h30 ngày 6/3/2020 (giờ Việt Nam):
87 quốc gia và vùng lãnh thổ có người mắc bệnh.
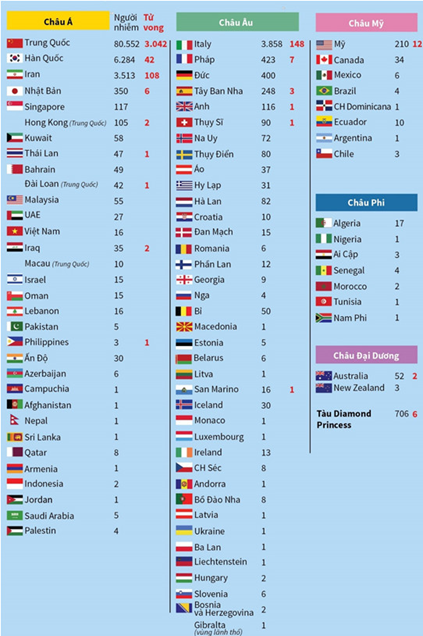
Tính đến 9h30 ngày 6/3/2020 (giờ Việt Nam), quốc gia nào ngoài Trung Quốc có số ca nhiễm Covid-19 cao nhất?
 Xem đáp án
Xem đáp án
Dựa vào bảng số liệu ta có:
• Italy có 3858 ca nhiễm. • Hàn Quốc có 6284 ca nhiễm.
• Iran có 3513 ca nhiễm. • Mỹ có 210 ca nhiễm.
Như vậy, ngoài Trung Quốc thì Hàn Quốc có số ca nhiễm Covid-19 cao nhất.
Chọn B
Câu 2:
 Xem đáp án
Xem đáp án
Ta có \(s' = gt\).
Vận tốc tức thời tại thời điểm \(t = 5{\mkern 1mu} \,s\) là: \(v\left( 5 \right) = s'\left( 5 \right) = 5g = 49{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\). Chọn D.
Câu 3:
 Xem đáp án
Xem đáp án
Ta có: \[{\log _2}\left( {1 - x} \right) = 2 \Leftrightarrow 1 - x = 4 \Leftrightarrow x = - 3\]. Chọn B.
Câu 4:
 Xem đáp án
Xem đáp án
Ta có \(\left\{ {\begin{array}{*{20}{l}}{2{x^2} - 5xy + 2{y^2} = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\\{2{x^2} - {y^2} = 7{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}} \right.\)
Khi đó \(\left( 1 \right) \Leftrightarrow \left( {2x - y} \right)\left( {x - 2y} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 2x}\\{x = 2y}\end{array}} \right.\)
• Với \(y = 2x\), ta có: \(\left( 2 \right) \Leftrightarrow 2{x^2} - {\left( {2x} \right)^2} = 7 \Leftrightarrow - 2{x^2} = 7{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)\)
• Với \(x = 2y\), ta có: \(\left( 2 \right) \Leftrightarrow 2.{\left( {2y} \right)^2} - {y^2} = 7 \Leftrightarrow 7{y^2} = 7 \Leftrightarrow y = \pm 1\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 1 \Rightarrow x = 2}\\{y = - 1 \Rightarrow x = - 2}\end{array}} \right..\)
Vậy hệ phương trình đã cho có hai nghiệm \(\left( {1\,;\,{\mkern 1mu} {\mkern 1mu} 2} \right)\) và \(\left( { - 1\,;\,{\mkern 1mu} {\mkern 1mu} - 2} \right).\) Chọn D.
Câu 5:
 Xem đáp án
Xem đáp án
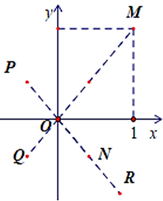
Gọi số phức \(z = a + bi{\mkern 1mu} {\mkern 1mu} \,\left( {a,b \in \mathbb{R}} \right)\) thì điểm \(N\left( {a\,;\,b} \right)\).
Khi đó số phức \(\frac{1}{z} = \frac{1}{{a + bi}} = \frac{{a - bi}}{{\left( {a + bi} \right)\left( {a - bi} \right)}} = \frac{{a - bi}}{{{a^2} + {b^2}}} = \frac{a}{{{a^2} + {b^2}}} - \frac{b}{{{a^2} + {b^2}}} \cdot i\)
Nên điểm biểu diễn số phức \(\frac{1}{z}\) có tọa độ \(\left( {\frac{a}{{{a^2} + {b^2}}}; - \frac{b}{{{a^2} + {b^2}}}} \right)\).
Vì điểm \(N\left( {a\,;\,b} \right)\) thuộc góc phần tư thứ (IV) tức là \(a > 0\,;\,\,b < 0\).
Suy ra \(\frac{a}{{{a^2} + {b^2}}} > 0;{\mkern 1mu} - \frac{b}{{{a^2} + {b^2}}} > 0\) nên điểm biểu diễn số phức \(\frac{1}{z}\) thuộc góc phần tư thứ (I). Từ hình vẽ chỉ có điểm \(M\) thỏa mãn. Chọn D.
Câu 6:
 Xem đáp án
Xem đáp án
Ta có \(\overrightarrow {AB} = \left( {1\,;\, - 2\,;\,{\mkern 1mu} 2} \right)\).
Mặt phẳng \(\left( P \right)\) cần tìm vuông góc với \(AB\) nên nó nhận vectơ \(\left( {1\,;\, - 2\,;\,{\mkern 1mu} 2} \right)\) làm VTPT.
Do đó \(\left( P \right)\) đi qua \[A\left( {1\,;{\mkern 1mu} {\mkern 1mu} \,2\,;{\mkern 1mu} {\mkern 1mu} \,3} \right)\] và vuông góc với \(AB\) có phương trình:
\(x - 1 - 2\left( {y - 2} \right) + 2\left( {z - 3} \right) = 0\) \( \Leftrightarrow x - 2y + 2z - 3 = 0.\) Chọn D.
Câu 7:
 Xem đáp án
Xem đáp án
Ta có \[AB = \sqrt {{3^2} + {2^2} + {{\left( { - 3} \right)}^2}} = \sqrt {22} \]. Chọn C.
Câu 8:
 Xem đáp án
Xem đáp án
TXĐ: \(D = \left( {1\,;{\mkern 1mu} {\mkern 1mu} \, + \infty } \right)\)
\(\frac{{{x^2}}}{{\sqrt {x - 1} }} < \frac{{2x + 8}}{{\sqrt {x - 1} }}\)\( \Leftrightarrow \frac{{{x^2} - 2x - 8}}{{\sqrt {x - 1} }} < 0\)
\( \Leftrightarrow {x^2} - 2x - 8 < 0\) (vì \(\sqrt {x - 1} > 0\) với mọi \(x \in D\))
\( \Leftrightarrow - 2 < x < 4\).
Mà \(x \in \mathbb{Z}\,,{\mkern 1mu} {\mkern 1mu} \,x > 1 \Rightarrow x \in \left\{ {2\,;{\mkern 1mu} {\mkern 1mu} \,3} \right\}\).
Vậy có 2 giá trị nguyên của \(x\) thỏa mãn điều kiện đề bài. Chọn A.
Câu 9:
 Xem đáp án
Xem đáp án
Ta có \[\cos 2x + 5\sin x - 4 = 0 \Leftrightarrow 1 - 2{\sin ^2}x + 5\sin x - 4 = 0\]
\[ \Leftrightarrow - 2{\sin ^2}x + 5\sin x - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sin x = 1}\\{\sin {\mkern 1mu} x = \frac{3}{2}{\mkern 1mu} {\mkern 1mu} \left( {vo{\mkern 1mu} {\mkern 1mu} nghiem} \right)}\end{array}} \right. \Leftrightarrow x = \frac{\pi }{2} + k2\pi ,{\mkern 1mu} {\mkern 1mu} \,k \in \mathbb{Z}.\]Chọn D.
Câu 10:
Litva sẽ tham gia vào cộng đồng chung châu Âu sử dụng đồng Euro là đồng tiền chung vào ngày 01 tháng 01 năm 2015. Để kỷ niệm thời khắc lịch sử chung này, chính quyền đất nước này quyết định dùng \[122\,\,550\] đồng tiền xu Litas Lithuania cũ của đất nước để xếp một mô hình kim tự tháp (như hình vẽ bên). Biết rằng tầng dưới cùng có \[4\,\,901\] đồng và cứ lên thêm một tầng thì số đồng xu giảm đi 100 đồng. Hỏi mô hình Kim tự tháp này có tất cả bao nhiêu tầng?

 Xem đáp án
Xem đáp án
Bài toán là bài tập về cấp số cộng nếu ta coi số đồng xu ở tầng dưới cùng là số hạng đầu tiên, với công sai là hiệu số đồng xu của tầng 2 tầng liền kề.
Khi đó, ta có một cấp số cộng với \({u_1} = 4901\) và công sai \(d = - 100\).
Gọi số tầng của kim tự tháp đó là \(n{\mkern 1mu} {\mkern 1mu} \left( {n \in {\mathbb{N}^*}} \right)\).
Khi đó, tổng số đồng xu của \(n\) tầng đó là \({S_n} = 122550\) nên ta có: \({S_n} = \frac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right]n}}{2}\)
\( \Leftrightarrow 122\,\,550 = \frac{{\left[ {2 \cdot 4\,\,901 + \left( {n - 1} \right)\left( { - 100} \right)} \right] \cdot n}}{2}\)\[ \Leftrightarrow 245\,\,100 = \left[ {2 \cdot 4\,\,901 - 100n + 100} \right] \cdot n\]
\( \Leftrightarrow 245\,\,100 = \left[ {9\,\,902 - 100n} \right].n\)\( \Leftrightarrow 100{n^2} - 9\,\,902n + 245\,\,100 = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{n = 50{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\\{n = \frac{{2451}}{{50}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\end{array}} \right.\).
Vậy mô hình kim tự tháp đã cho có 50 tầng. Chọn B.
Câu 11:
 Xem đáp án
Xem đáp án
Ta có \(\frac{{{x^3} + {x^2} - 5}}{{{x^2} + x - 2}}\)\( = \frac{{\left( {{x^3} + {x^2} - 2x} \right) + 2x - 5}}{{{x^2} + x - 2}}\)\( = x + \frac{{2x - 5}}{{\left( {x - 1} \right)\left( {x + 2} \right)}}\).
Đặt \(\frac{{2x - 5}}{{\left( {x - 1} \right)\left( {x + 2} \right)}} = \frac{A}{{x - 1}} + \frac{B}{{x + 2}}\)\( \Leftrightarrow \frac{{2x - 5}}{{\left( {x - 1} \right)\left( {x + 2} \right)}} = \frac{{A\left( {x + 2} \right) + B\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 2} \right)}}\)
\( \Leftrightarrow 2x - 5 = \left( {A + B} \right)x + 2A - B\).
Đồng nhất hệ số 2 vế của phương trình ta được \(\left\{ {\begin{array}{*{20}{l}}{A + B = 2}\\{2A - B = - 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{A = - 1}\\{B = 3}\end{array}} \right.\)
\( \Rightarrow \frac{{{x^3} + {x^2} - 5}}{{{x^2} + x - 2}} = x - \frac{1}{{x - 1}} + \frac{3}{{x + 2}}\)\( \Rightarrow \int {\frac{{{x^3} + {x^2} - 5}}{{{x^2} + x - 2}}dx} = \int {\left( {x - \frac{1}{{x - 1}} + \frac{3}{{x + 2}}} \right)dx} \)
\( = \frac{{{x^2}}}{2} - \ln \left| {x - 1} \right| + 3\ln \left| {x + 2} \right| + C.\) Chọn C.
Câu 12:
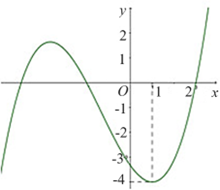
Cho hàm số \(f\left( x \right)\) có đồ thị như hình vẽ bên. Bất phương trình \(f\left( {{e^x}} \right) < m\left( {3{e^x} + 2019} \right)\) có nghiệm \(x \in \left( {0\,;\,\,1} \right)\) khi và chỉ khi
 Xem đáp án
Xem đáp án
Xét bất phương trình \(f\left( {{e^x}} \right) < m\left( {3{e^x} + 2019} \right)\). (*)
Đặt \({e^x} = t\left( {t > 0} \right)\) với: \(x \in \left( {0;1} \right) \Rightarrow t \in \left( {{e^0};\,\,{e^1}} \right) \Rightarrow t \in \left( {1;\,\,e} \right)\).
Ta được bất phương trình \(f\left( t \right) < m\left( {3t + 2019} \right) \Leftrightarrow m > \frac{{f\left( t \right)}}{{3t + 2019}}\) (vì \(3t + 2019 > 0\) với \(\left. {t \in \left( {1;e} \right)} \right)\)
Để bất phương trình (*) có nghiệm \(x \in \left( {0;1} \right)\) thì bất phương trình (1) có nghiệm \(t \in \left( {1\,;\,\,e} \right)\).
Ta xét hàm \(g\left( t \right) = \frac{{f\left( t \right)}}{{3t + 2019}}\) trên \(\left( {1\,;\,\,e} \right)\). Ta có \(g'\left( t \right) = \frac{{f'\left( t \right)\left( {3t + 2019} \right) - 3f\left( t \right)}}{{{{\left( {3t + 2019} \right)}^2}}}\).
Nhận xét rằng đồ thị hàm số \(y = f\left( t \right)\) có tính chất giống với đồ thị hàm số \(y = f\left( x \right)\) nên xét trên khoảng \(\left( {1\,;\,\,e} \right)\) ta thấy rằng \(f\left( t \right) < 0\) và đồ thị hàm số đi lên từ trái qua phải hay hàm số đồng biến trên \(\left( {1\,;\,\,e} \right)\) nên \(f'\left( t \right) > 0\).
Từ đó \(g'\left( t \right) = \frac{{f'\left( t \right)\left( {3t + 2019} \right) - 3f\left( t \right)}}{{{{\left( {3t + 2019} \right)}^2}}} > 0\) với \(t \in \left( {1\,;\,\,e} \right)\) hay hàm số \[g\left( t \right)\] đồng biến trên \(\left( {1\,;\,\,e} \right).\)
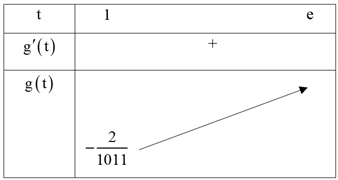
Từ bảng biến thiên ta thấy để bất phương trình \[m > \frac{{f\left( t \right)}}{{3t + 2019}}\] với \(t \in \left( {1\,;\,\,e} \right)\) thì \(m > \mathop {\min }\limits_{\left[ {1;\,\,e} \right]} g\left( t \right) \Leftrightarrow m > - \frac{2}{{1011}}.\) Chọn C.
Câu 13:
 Xem đáp án
Xem đáp án
Thời điểm máy bay đạt vận tốc 200 m/s là: \({t^2} + 10t = 200 \Leftrightarrow t = 10{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Quãng đường máy bay di chuyển trên đường băng từ thời điểm \(t = 0{\mkern 1mu} {\mkern 1mu} \left( s \right)\) tới thời điểm \(t = 10{\mkern 1mu} {\mkern 1mu} \left( s \right)\) là: \(s = \int\limits_0^{10} {v\left( t \right)dx} = \int\limits_0^{10} {\left( {{t^2} + 10t} \right)dt} = \frac{{2500}}{3}{\mkern 1mu} {\mkern 1mu} \left( m \right)\). Chọn C.
Câu 14:
 Xem đáp án
Xem đáp án
Ông Bá Kiến gửi 100 triệu với lãi suất \[6,7\% \] nên sau \[n\] năm số tiền của ông là \({A_n} = 100 \cdot 1,{067^n}\).
Anh giáo Thứ gửi 20 triệu với lãi suất \[7,6\% \] thì sau \[n\] năm số tiền của anh là \({B_n} = 20.1,{076^n}\).
Để số tiền của anh giáo Thứ lớn hơn ông Bá Kiến thì
\(20 \cdot 1,{076^n} > 100 \cdot 1,{067^n} \Leftrightarrow {\left( {\frac{{1,076}}{{1,067}}} \right)^n} > 5 \Leftrightarrow n > 191,6\). Chọn B.
Vậy phải sau ít nhất 192 năm thì số tiền của anh giáo Thứ mới nhiều hơn số tiền của ông Bá Kiến.
Câu 15:
 Xem đáp án
Xem đáp án
ĐKXĐ: \(\left\{ {\begin{array}{*{20}{l}}{{{\log }_3}x > 0}\\{x > 0}\end{array}} \right. \Rightarrow x > 1\).
Ta có: \({\log _{\frac{1}{2}}}\left( {{{\log }_3}x} \right) > 0\)\( \Leftrightarrow {\log _3}x < 1 \Leftrightarrow x < 3\)
Kết hợp ĐKXĐ ta có: \(1 < x < 3\)
Do đó, tập nghiệm của bất phương trình là \(\left( {1\,;\,\,3} \right)\).
Do đó \(a = 1\,;\,\,b = 3\) nên \(a + b = 1 + 3 = 4\). Chọn A.
Câu 16:
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm: \[{x^2} - 4x + 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 3}\end{array}} \right.\].
Vậy diện tích hình phẳng giới hạn bởi \[y = {x^2} - 4x + 3,\] \[x = 0,{\mkern 1mu} {\mkern 1mu} \,x = 3\] là
\[S = \int\limits_0^3 {\left| {{x^2} - 4x + 3} \right|dx} \]\[ = \left| {\int\limits_0^1 {\left( {{x^2} - 4x + 3} \right)dx} } \right| + \left| {\int\limits_1^3 {\left( {{x^2} - 4x + 3} \right)dx} } \right|\]\[{\mkern 1mu} = \left| {\frac{4}{3}} \right| + \left| { - \frac{4}{3}} \right| = \frac{8}{3}.\]
Chọn D.
Câu 17:
 Xem đáp án
Xem đáp án
Hàm số \(y = \frac{{{x^3}}}{3} - \left( {m - 1} \right){x^2} + 3\left( {m - 1} \right)x + 1\) xác định trên \(\left( {1\,;\,\, + \infty } \right)\).
Ta có \(y' = {x^2} - 2\left( {m - 1} \right)x + 3\left( {m - 1} \right)\)
Để hàm số đồng biến trên \(\left( {1\,;\,\, + \infty } \right)\) thì \(y' \ge 0{\mkern 1mu} {\mkern 1mu} \,\,\forall x \in \left( {1\,;\,\, + \infty } \right)\)
\( \Leftrightarrow {x^2} - 2\left( {m - 1} \right)x + 3\left( {m - 1} \right) \ge 0\,\,{\mkern 1mu} \forall x \in \left( {1\,;\,\, + \infty } \right)\) (*).
Ta có \(\Delta ' = {\left( {m - 1} \right)^2} - 3\left( {m - 1} \right) = {m^2} - 5m + 4\).
TH1: \(\Delta ' \le 0 \Leftrightarrow {m^2} - 5m + 4 \le 0 \Leftrightarrow 1 \le m \le 4\), khi đó \(y' \ge 0\,\,{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}\) nên thỏa mãn (*).
TH2: \(\Delta ' > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 4}\\{m < 1}\end{array}} \right.\), khi đó phương trình \(y' = 0\) có hai nghiệm phân biệt \({x_1} < {x_2}\).
Áp dụng định lí Viète, ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m - 1} \right)}\\{{x_1}{x_2} = 3\left( {m - 1} \right)}\end{array}} \right.\).
Khi đó ta có \(y' \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x \ge {x_2}}\\{x \le {x_1}}\end{array}} \right.\), nên hàm số đã cho đồng biến trên \(\left( { - \infty \,;\,\,{x_1}} \right)\) và \(\left( {{x_2}\,;\,\, + \infty } \right).\)
Để hàm số đồng biến trên \(\left( {1\,;\,\, + \infty } \right)\) thì \(\left( {1\,;\,\, + \infty } \right) \subseteq \left( {{x_2}\,;\,\, + \infty } \right)\)\( \Rightarrow {x_1} < {x_2} \le 1\)
Khi đó ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} < 2}\\{\left( {{x_1} - 1} \right)\left( {{x_2} - 1} \right) \ge 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} < 2}\\{{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 \ge 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2\left( {m - 1} \right) < 2}\\{3\left( {m - 1} \right) - 2\left( {m - 1} \right) + 1 \ge 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m - 1 < 1}\\{m - 1 + 1 \ge 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 2}\\{m \ge 0}\end{array}} \right. \Leftrightarrow 0 \le m < 2\).
Kết hợp 2 TH ta có \(0 \le m \le 4\). Mà \[m \in \mathbb{Z} \Rightarrow m \in \left\{ {0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4} \right\}\].
Vậy có 5 giá trị của \[m\] thỏa mãn yêu cầu bài toán. Chọn C.
Câu 18:
 Xem đáp án
Xem đáp án
Đặt \(z = a + bi \Rightarrow \bar z = a - bi\).
Theo bài ra ta có: \(\left( {2 - 3i} \right)z - 7i\bar z = 22 - 20i\)\( \Leftrightarrow \left( {2 - 3i} \right)\left( {a + bi} \right) - 7i\left( {a - bi} \right) = 22 - 20i\)
\( \Leftrightarrow 2a + 2bi - 3ai + 3b - 7ai - 7b = 22 - 20i\)\( \Leftrightarrow 2a - 4b + \left( {2b - 10a} \right)i = 22 - 20i\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a - 4b = 22}\\{2b - 10a = - 20}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 5}\end{array}} \right.\)\( \Rightarrow z = 1 - 5i\).
Vậy \(a + b = 1 + \left( { - 5} \right) = - 4\). Chọn B.
Câu 19:
 Xem đáp án
Xem đáp án
Đặt \(z = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\)
Ta có: \(\left| {z - i} \right| = \left| {2 - 3i - z} \right|\)\( \Leftrightarrow \left| {x + yi - i} \right| = \left| {2 - 3i - \left( {x + yi} \right)} \right|\)
\( \Leftrightarrow \left| {x + \left( {y - 1} \right)i} \right| = \left| {2 - x - \left( {y + 3} \right)i} \right|\)\( \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \sqrt {{{\left( {2 - x} \right)}^2} + {{\left( {y + 3} \right)}^2}} \)
\( \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {2 - x} \right)^2} + {\left( {y + 3} \right)^2}\)\( \Leftrightarrow {x^2} + {y^2} - 2y + 1 = 4 - 4x + {x^2} + {y^2} + 6y + 9\)
\( \Leftrightarrow 4x - 8y - 12 = 0\)\( \Leftrightarrow x - 2y - 3 = 0\).
Vậy tập hợp biểu diễn số phức \(z\) là đường thẳng \(x - 2y - 3 = 0.\) Chọn A.
Câu 20:
 Xem đáp án
Xem đáp án
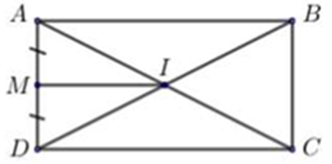
Ta có \[\overrightarrow {IM} = \left( { - 1\,;\,\, - 2} \right)\]
\[ \Rightarrow IM = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \Rightarrow AB = 2IM = 2\sqrt 5 \]
\[S = 10 \Rightarrow AB \cdot AD = 10 \Leftrightarrow 2\sqrt 5 \cdot AD = 10 \Rightarrow AD = \sqrt 5 \]
\(AD\) qua \(M\left( {0\,;\,\, - 1} \right)\) và \(AD \bot \overrightarrow {IM} = \left( { - 1\,;\,\, - 2} \right)\)
\( \Rightarrow \overrightarrow {{n_{AD}}} = \left( {1\,;\,\,2} \right) \Rightarrow AD:{\mkern 1mu} \,x + 2y + 2 = 0\).
\(\overrightarrow {DA} = \left( {4t + 4\,;\,\, - 2 - 2t} \right) \Rightarrow D{A^2} = {\left( {4t + 4} \right)^2} + {\left( { - 2 - 2t} \right)^2} = 5\)
\( \Leftrightarrow 20{t^2} + 40t + 15 = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{t = \frac{{ - 1}}{2} \Rightarrow D\left( { - 1\,;\,\,\frac{{ - 1}}{2}} \right)}\\{t = \frac{{ - 3}}{2} \Rightarrow D\left( {1\,;\,\,\frac{{ - 3}}{2}} \right)}\end{array}} \right.\). Chọn B.
Câu 21:
 Xem đáp án
Xem đáp án
Xét phương trình đường tròn: \({x^2} + {y^2} - 8x + 10y + m = 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = - 5}\\{c = m}\end{array}} \right.\).
Ta có: \({a^2} + {b^2} - c = {R^2}\)\( \Rightarrow {4^2} + {\left( { - 5} \right)^2} - m = {7^2} \Leftrightarrow m = - 8\). Chọn C.
Câu 22:
 Xem đáp án
Xem đáp án
Mặt phẳng \(\left( \alpha \right):2x - y + 3z + 4 = 0\) có 1 VTPT là \(\vec n\left( {2\,;\,\, - 1\,;\,\,3} \right)\).
Gọi \[\left( P \right)\] là mặt phẳng cần tìm. Do \[\left( P \right)\] song song \[Oy\] và vuông góc với \(\left( \alpha \right)\) nên \[\left( P \right)\] có VTPT là \(\overrightarrow {{n_1}} = \left[ {\vec n\,;\,\,\vec j\left( {0\,;\,\,1\,;\,\,0} \right)} \right] = \left( { - 3\,;\,\,0\,;\,\,2} \right).\)
Mặt phẳng \[\left( P \right)\] đi qua \(A\left( {2\,;\,\, - 1\,;\,\,2} \right)\), có VTPT \(\overrightarrow {{n_1}} = \left( { - 3\,;\,\,0\,;\,\,2} \right)\) có phương trình là:
\( - 3\left( {x - 2} \right) + 0 + 2\left( {z - 2} \right) = 0 \Leftrightarrow \) \(3x - 2z - 2 = 0\). Chọn C.
Câu 23:
 Xem đáp án
Xem đáp án
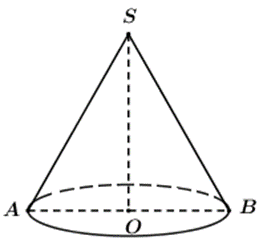
Giả sử thiết diện qua trục là tam giác \(SAB\), \(O\) là tâm đường tròn đáy nên \(O\) là trung điểm của \(AB\).
Tam giác \(SAB\) vuông tại \(S\) nên
\({S_{\Delta SAB}} = \frac{1}{2}SA.SB = \frac{1}{2}S{A^2} = 8 \Leftrightarrow SA = 4 = l\)
\( \Rightarrow AB = SA\sqrt 2 = 4\sqrt 2 \Rightarrow r = OA = 2\sqrt 2 \).
Vậy diện tích xung quanh hình nón là: \({S_{xq}} = \pi rl = \pi \cdot 2\sqrt 2 \cdot 4 = 8\sqrt 2 \pi \). Chọn B.
Câu 24:
 Xem đáp án
Xem đáp án
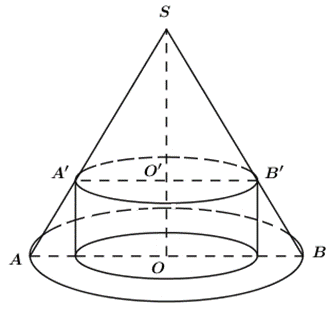
Theo bài ra ta có \(SO = 10\,,{\mkern 1mu} {\mkern 1mu} \,OA = 5\).
Đặt \(O'A' = r{\rm{ }}\left( {0 < r < 5} \right)\)
Áp dụng định lí Thalès, ta có:
\(\frac{{O'A'}}{{OA}} = \frac{{SO'}}{{SO}} \Rightarrow \frac{r}{5} = \frac{{SO'}}{{10}} \Leftrightarrow SO' = 2r \Rightarrow OO' = 10 - 2r\)
Khi đó thể tích khối trụ là:
\(V = \pi \cdot O'{A'^2} \cdot OO' = \pi \cdot {r^2}\left( {10 - 2r} \right) = 2\pi \left( { - {r^3} + 5{r^2}} \right)\).
Xét hàm số \(f\left( r \right) = - {r^3} + 5{r^2}\) trên \(\left( {0;5} \right)\) ta có \(f'\left( r \right) = - 3{r^2} + 10r = 0 \Leftrightarrow \left[ \begin{array}{l}r = 0{\rm{ }}\left( {ktm} \right)\\r = \frac{{10}}{3}\end{array} \right.\).
Vậy để thể tích khối trụ đạt giá trị lớn nhất thì bán kính khối trụ bằng \(\frac{{10}}{3}\). Chọn B.
Câu 25:
 Xem đáp án
Xem đáp án
![Cho khối lăng trụ tam giác đều \[ABC.A'B'C'\] có cạnh đáy là \[2a\] và khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {A'BC} \right)\] bằng \[a\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/08/blobid3-1722738576.png)
Gọi \(M\) là trung điểm của \[BC\] ta có
\[\left\{ {\begin{array}{*{20}{l}}{BC \bot AM}\\{BC \bot AA'}\end{array}} \right. \Rightarrow BC \bot \left( {A'BC} \right)\]
Trong \[\left( {A'BC} \right)\] kẻ \[AH \bot A'M{\mkern 1mu} {\mkern 1mu} \,\left( {H \in A'M} \right)\] ta có:
\[\left\{ {\begin{array}{*{20}{l}}{AH \bot BC}\\{AH \bot A'M}\end{array}} \right. \Rightarrow AH \bot \left( {A'BC} \right)\]\[ \Rightarrow d\left( {A,\left( {A'BC} \right)} \right) = AH = a\]
Vì tam giác \(ABC\) đều cạnh \(2a\) nên \(AM = 2a \cdot \frac{{\sqrt 3 }}{2} = a\sqrt 3 \) và \({S_{ABC}} = {\left( {2a} \right)^2}\frac{{\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Áp dụng hệ thức lượng trong tam giác vuông \(AA'M\) ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A'{A^2}}} + \frac{1}{{A{M^2}}} \Rightarrow \frac{1}{{{a^2}}} = \frac{1}{{A'{A^2}}} + \frac{1}{{3{a^2}}}\)\( \Rightarrow \frac{1}{{A'{A^2}}} = \frac{2}{{3{a^2}}} \Rightarrow A'A = \frac{{a\sqrt 6 }}{2}\).
Vậy \({V_{ABC.A'B'C'}} = A'A \cdot {S_{ABC}} = \frac{{a\sqrt 6 }}{2} \cdot {a^2}\sqrt 3 = \frac{{3{a^3}\sqrt 2 }}{2}\). Chọn D.
Câu 26:
 Xem đáp án
Xem đáp án
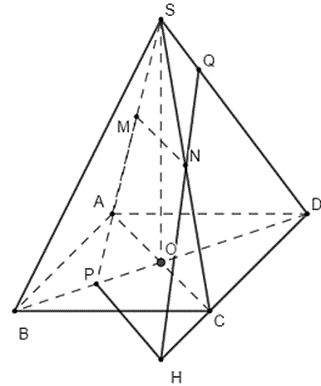
Trong \(\left( {ABCD} \right)\) lấy \(PH\,{\rm{//}}\,MN\)\(\left( {H \in CD} \right)\)
Trong \(\left( {SCD} \right)\) gọi \(Q = NH \cap SD\)
Áp dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(QNH\) ta có: \(\frac{{HD}}{{HC}} \cdot \frac{{NC}}{{NS}} \cdot \frac{{QS}}{{QD}} = 1.\)
Mà \(N\) là trung điểm của \(SC\) nên \(\frac{{NC}}{{NS}} = 1\).
Mặt khác áp dụng định lí Thalès trong tam giác \(DPH\) ta có \(\frac{{HD}}{{HC}} = \frac{{DP}}{{OP}} = 3\) (vì \(P\) là trung điểm của \(OB\)).
Do đó ta có \(\frac{{QS}}{{QD}} = \frac{1}{3} \Rightarrow \frac{{SQ}}{{SD}} = \frac{1}{4}\). Chọn A.
Câu 27:
 Xem đáp án
Xem đáp án
Gọi \(M\left( {x\,;\,\,y\,;\,\,z} \right)\). Theo bài ra ta có: \(2M{A^2} + M{B^2} = 165\)
\( \Leftrightarrow 2\left[ {{{\left( {x - 1} \right)}^2} + {{\left( {y - 2} \right)}^2} + {{\left( {z - 3} \right)}^2}} \right] + \left[ {{{\left( {x - 4} \right)}^2} + {{\left( {y + 7} \right)}^2} + {{\left( {z + 9} \right)}^2}} \right] = 165\)
\( \Leftrightarrow 3{x^2} + 3{y^2} + 3{z^2} - 12x + 6y + 6z + 9 = 0\)\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 4x + 2y + 2z + 3 = 0\).
Do đó tập hợp các điểm \(M\) thỏa mãn yêu cầu bài toán là mặt cầu tâm nên \(a = 2\,,{\mkern 1mu} {\mkern 1mu} \,b = - 1\,,{\mkern 1mu} {\mkern 1mu} \,c = - 1,\) bán kính \(R = \sqrt {4 + 1 + 1 - 3} = \sqrt 3 \).
Vậy \(T = {a^2} + {b^2} + {c^2} + {R^2} = 4 + 1 + 1 + 3 = 9\). Chọn A.
Câu 28:
 Xem đáp án
Xem đáp án
Đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{z}{{ - 2}}\) có 1 VTCP là \(\overrightarrow {{u_d}} = \left( {2\,;\,\,1\,;\,\, - 2} \right)\), đây cũng là VTCP của đường thẳng đi qua \[A\] và song song với \[d.\]
Đường thẳng qua \[A\] và song song với \[d\] nhận \(\vec u = \left( {2\,;\,\,1\,;\,\, - 2} \right)\) là VTCP, có phương trình tham số: \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 1 + t}\\{z = - 2 - 2t}\end{array}} \right.\). Chọn B.
Câu 29:
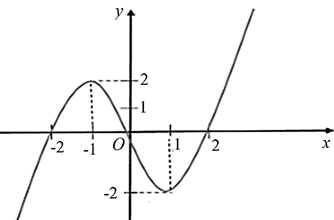
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R},\) có đồ thị như hình vẽ. Hàm số \(g\left( x \right) = f\left( {{x^2} - 2} \right)\) có bao nhiêu điểm cực tiểu?
 Xem đáp án
Xem đáp án
Dựa vào đồ thị hàm số ta thấy: Hàm số có 2 điểm cực trị \(x = - 1,{\mkern 1mu} {\mkern 1mu} \,x = 1\).
Do đó \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 1}\end{array}} \right.\). Ta có \(g'\left( x \right) = 2x \cdot f'\left( {{x^2} - 2} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{f'\left( {{x^2} - 2} \right) = 0}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} - 2 = 1}\\{{x^2} - 2 = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm \sqrt 3 }\\{x = \pm 1}\end{array}} \right.\).
Ta có bảng xét dấu \(g'\left( x \right)\) như sau:

Dựa vào bảng xét dấu ta thấy, \(g'\left( x \right)\) đổi dấu từ âm sang dương khi đi qua các điểm \(x = - \sqrt 3 ,\) \(x = 0\,,\,\,x = \sqrt 3 \).
Vậy hàm số \(y = g\left( x \right)\) có 3 điểm cực tiểu. Chọn A.
Câu 30:
 Xem đáp án
Xem đáp án
Dễ thấy hai điểm \(A,{\mkern 1mu} {\mkern 1mu} B\) nằm cùng phía đối với \(\left( {Oxy} \right)\), điểm \[M\left( {a\,;\,\,b\,;\,\,0} \right) \in \left( {Oxy} \right)\].
Gọi \(A'\) là điểm đối xứng với \(A\) qua \(\left( {Oxy} \right)\)\( \Rightarrow A'\left( {1\,;\,\,2\,;\,\, - 3} \right)\).
Theo tính chất đối xứng ta có \(MA = MA'\).
Do đó \(MA + MB = MA' + MB \ge A'B\) (bất đẳng thức tam giác).
Dấu “=” xảy ra \( \Rightarrow M \in A'B\). Hay \(M,{\mkern 1mu} {\mkern 1mu} \,A',{\mkern 1mu} {\mkern 1mu} \,B\) thẳng hàng \( \Rightarrow \overrightarrow {A'M} \,,\,\,{\mkern 1mu} {\mkern 1mu} \overrightarrow {A'B} \) cùng phương.
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {A'M} = \left( {a - 1\,;\,\,b - 2\,;\,\,3} \right)}\\{\overrightarrow {A'B} = \left( {4\,;\,\,4\,;\,\,4} \right)}\end{array}} \right.\)\( \Rightarrow \frac{{a - 1}}{4} = \frac{{b - 2}}{4} = \frac{3}{4}\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = 5}\end{array}} \right.\)
\( \Rightarrow M\left( {4\,;\,\,5\,;\,\,0} \right)\). Vậy \(OM = \sqrt {{4^2} + {5^2} + {0^2}} = \sqrt {41} \). Chọn B.
Câu 31:
 Xem đáp án
Xem đáp án
Xét hàm số \(f\left( x \right) = 3{x^4} - 8{x^3} - 6{x^2} + 24x - m\).
Đồ thị hàm số \(f\left( x \right)\) có nhiều nhất 3 điểm cực trị và cắt trục hoành tại nhiều nhất 4 điểm.
Do đó để đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) có 7 điểm cực trị thì đồ thị hàm số \(f\left( x \right)\) phải cắt trục hoành tại 4 điểm phân biệt và có 3 điểm cực trị.
Suy ra, đồ thị hàm số \(f\left( x \right)\) phải cắt trục hoành tại 4 điểm phân biệt (vì khi đó chắc chắn hàm số \(y = f\left( x \right)\) sẽ có 3 điểm cực trị) .
Khi đó, phương trình \(3{x^4} - 8{x^3} - 6{x^2} + 24x - m = 0 \Leftrightarrow 3{x^4} - 8{x^3} - 6{x^2} + 24x = m{\mkern 1mu} {\mkern 1mu} \,\,\left( * \right)\) phải có 4 nghiệm phân biệt.
Xét hàm số \(g\left( x \right) = 3{x^4} - 8{x^3} - 6{x^2} + 24x\) ta có \(g'\left( x \right) = 12{x^3} - 24{x^2} - 12x + 24 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 1}\\{x = 2}\end{array}} \right.\)
Ta có bảng biến thiên:
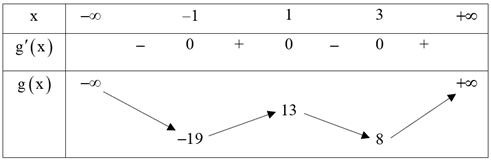
Dựa vào bảng biến thiên, ta thấy phương trình (*) có 4 nghiệm phân biệt \( \Leftrightarrow 8 < m < 13\).
Mà \(m \in \mathbb{Z}\) nên \[m \in S = \left\{ {9\,;\,\,10\,;\,\,11\,;\,\,12} \right\}\].
Vậy tổng tất cả các phần tử của \(S\) là \(9 + 10 + 11 + 12 = 42\). Chọn D.
Câu 32:
 Xem đáp án
Xem đáp án
Ta có \(\sqrt {2{x^2} - 2x - m} = x + 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + 2 \ge 0}\\{2{x^2} - 2x - m = {{\left( {x + 2} \right)}^2}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge - 2}\\{2{x^2} - 2x - m = {x^2} + 4x + 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge - 2}\\{{x^2} - 6x - 4 = m}\end{array}} \right..\)
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số \(y = {x^2} - 6x - 4\) và đường thẳng \(y = m\) với \(x \ge - 2.\)
Xét hàm số \(y = {x^2} - 6x - 4\) ta có bảng biến thiên:
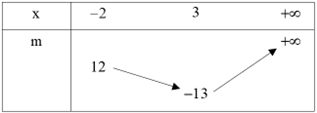
Từ bảng biến thiên suy ra để phương trình có nghiệm \(x \ge - 2\) thì \(m \ge - 13.\)
Lại có \(\left\{ {\begin{array}{*{20}{l}}{m \in \mathbb{Z}}\\{m < - 6}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{m \in \mathbb{Z}}\\{ - 13 \le m < - 6}\end{array}} \right. \Rightarrow m \in \left\{ { - 13\,;\,\,{\mkern 1mu} - 12\,;\,\, \ldots \,;\,\, - 7} \right\}\)
Do đó có 7 giá trị \(m\) thỏa mãn bài toán. Chọn C.
Câu 33:
 Xem đáp án
Xem đáp án
Ta có: \(\int\limits_1^3 {\left( {4 - x} \right)f\left( x \right)dx} = 4\int\limits_1^3 {f\left( x \right)dx} - \int\limits_1^3 {xf\left( x \right)dx} \)
Đặt \(t = 4 - x \Rightarrow dt = - dx\).
Đổi cận: \(\left\{ {\begin{array}{*{20}{l}}{x = 1 \Rightarrow t = 3}\\{x = 3 \Rightarrow t = 1}\end{array}} \right.\), khi đó ta có:
\(\int\limits_1^3 {\left( {4 - x} \right)f\left( x \right)dx} = - \int\limits_3^1 {tf\left( {4 - t} \right)dt} \)\( = \int\limits_1^3 {tf\left( {4 - t} \right)dt} = \int\limits_1^3 {tf\left( t \right)dt} \)
\( = \int\limits_1^3 {xf\left( x \right)dx} \) \( \Rightarrow \int\limits_1^3 {xf\left( x \right)dx} = 4\int\limits_1^3 {f\left( x \right)dx} - \int\limits_1^3 {xf\left( x \right)dx} \)
\( \Leftrightarrow 2\int\limits_1^3 {f\left( x \right)dx} = \int\limits_1^3 {xf\left( x \right)dx} = \left( { - 2} \right)\). Chọn C.
Câu 34:
 Xem đáp án
Xem đáp án
Gọi A là biến cố: “Xạ thủ đạt loại giỏi”
TH1: Xạ thủ được 30 điểm nên xạ thủ bắn trúng vòng 10 ba lần.
Do đó \[{P_1} = 0,{2^3} = 0,008\].
TH2: Xạ thủ được 29 điểm nên xạ thủ bắn trúng vòng 10 hai lần và vòng 9 một lần.
Do đó \[{P_2} = C_3^2 \cdot 0,{2^2} \cdot 0,25 = 0,03\]
TH3: Xạ thủ được 28 điểm nên xạ thủ bắn trúng vòng 10 hai lần và vòng 8 một lần hoặc Xạ thủ bắn trúng vòng 10 một lần, trúng vòng 9 hai lần
Do đó \({P_3} = C_3^2 \cdot 0,{2^2} \cdot 0,{15^1} + C_3^1 \cdot 0,{2^1} \cdot 0,{25^2} = 0,0555\).
Vậy \(P\left( A \right) = {P_1} + {P_2} + {P_3} = 0,0935\). Chọn C.
Câu 35:
 Xem đáp án
Xem đáp án
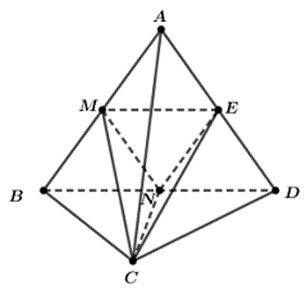
Ta có \({V_{ABCD}} = {V_{C.ABD}} = \frac{1}{3}{S_{ABD}} \cdot d\left( {C,\left( {ABD} \right)} \right)\)
\({V_{MNEC}} = {V_{C.MNE}} = \frac{1}{3}{S_{MNE}} \cdot d\left( {C,\left( {MNE} \right)} \right) = \frac{1}{3}{S_{MNE}} \cdot d\left( {C,\left( {ABD} \right)} \right)\)
\( \Rightarrow \frac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \frac{{\frac{1}{3}{S_{MNE}} \cdot d\left( {C,\left( {ABD} \right)} \right)}}{{\frac{1}{3}{S_{ABD}} \cdot d\left( {C,\left( {ABD} \right)} \right)}} = \frac{{{S_{MNE}}}}{{{S_{ABD}}}}\)
Dễ thấy \(\Delta MNE\) đồng dạng \(\Delta DAB\) theo tỉ số \(\frac{1}{2}\) nên \(\frac{{{S_{MNE}}}}{{{S_{ABD}}}} = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4}\).
Vậy \(\frac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \frac{{{S_{MNE}}}}{{{S_{ABD}}}} = \frac{1}{4}\). Chọn B.
Câu 36:
Hệ số góc của tiếp tuyến với đồ thị hàm số \(y = \ln \left( {x + 1} \right)\) tại điểm có hoành độ \(x = 2\) là
Đáp án: ……….
 Xem đáp án
Xem đáp án
Ta có \(y = \ln \left( {x + 1} \right) \Rightarrow y' = \frac{1}{{x + 1}} \Rightarrow y'\left( 2 \right) = \frac{1}{3}\).
Vậy hệ số góc của tiếp tuyến với đồ thị hàm số \(y = \ln \left( {x + 1} \right)\) tại điểm có hoành độ \(x = 2\) là \(\frac{1}{3}.\)
Đáp án: \[\frac{1}{3}.\]
Câu 37:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \[f'\left( x \right) = \left( {\ln x + 1} \right)\left( {{e^x} - 2019} \right)\left( {x + 1} \right)\] trên khoảng \[\left( {0\,;\,\, + \infty } \right)\]. Hỏi hàm số \[y = f\left( x \right)\] có bao nhiêu điểm cực trị?
Đáp án: ……….
 Xem đáp án
Xem đáp án
TXĐ: \(D = \left( {0\,;\,\, + \infty } \right)\).
Ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\ln x + 1 = 0}\\{{e^x} - 2019 = 0}\\{x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\ln x = - 1}\\{{e^x} = 2019}\\{x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{1}{e} \in \left( {0\,;\,\, + \infty } \right)}\\{x = \ln 2019 \in \left( {0\,;\,\, + \infty } \right)}\\{x = - 1 \notin \left( {0\,;\,\, + \infty } \right)}\end{array}} \right.\).
Vậy hàm số đã cho có 2 điểm cực trị.
Đáp án: 2.
Câu 38:
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} 2x - y - 2z - 9 = 0\) và \(\left( Q \right):{\mkern 1mu} 4x - 2y - 4z - 6 = 0\). Khoảng cách giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) bằng
Đáp án: ……….
 Xem đáp án
Xem đáp án
Vì \(\frac{2}{4} = \frac{{ - 1}}{{ - 2}} = \frac{{ - 2}}{{ - 4}} \ne \frac{{ - 9}}{{ - 6}}\) nên \(\left( P \right){\rm{//}}\left( Q \right)\).
Xét \(\left( P \right)\), cho \(x = z = 0 \Rightarrow y = - 9 \Rightarrow M\left( {0\,;\,\, - 9\,;\,\,0} \right) \in \left( P \right)\)
Vậy \(d\left( {\left( P \right),\left( Q \right)} \right) = d\left( {M,\left( Q \right)} \right) = \frac{{\left| { - 2 \cdot \left( { - 9} \right) - 6} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 4} \right)}^2}} }} = 2\).
Đáp án: 2.
Câu 39:
Lớp 11A có 15 học sinh nữ, 20 học sinh nam. Có bao nhiêu cách chọn 5 học sinh tham gia văn nghệ trong đó có ít nhất 3 học sinh nữ?
Đáp án: ……….
 Xem đáp án
Xem đáp án
Để chọn được 5 học sinh tham gia văn nghệ trong đó có ít nhất 3 học sinh nữ ta có các TH sau:
TH1: 3 học sinh nữ, 2 học sinh nam nên có \[C_{15}^3 \cdot C_{20}^2 = 86\,\,450\](cách).
TH2: 4 học sinh nữ, 1 học sinh nam nên có \(C_{15}^4 \cdot C_{20}^1 = 27\,\,300\) (cách).
TH3: 5 học sinh nữ nên có \(C_{15}^5 = 3003\) (cách).
Vậy có tất cả \(86\,\,450 + 27\,\,300 + 3\,\,003 = 116\,\,753\) (cách).
Đáp án: \[{\bf{116}}\,\,{\bf{753}}.\]
Câu 40:
Cho \(f\left( x \right)\) là một đa thức thỏa mãn \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{x - 2}} = 3\).
Tính \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{\left( {{x^2} - 4} \right)\left( {\sqrt {2f\left( x \right) + 6} + 3} \right)}}.\)
Đáp án: ……….
 Xem đáp án
Xem đáp án
Đặt \[g\left( x \right) = \frac{{f\left( x \right) - 15}}{{x - 2}}\]\[ \Rightarrow f\left( x \right) = \left( {x - 2} \right)g\left( x \right) + 15\]
\[ \Rightarrow \mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left[ {\left( {x - 2} \right)g\left( x \right) + 15} \right] = 15\].
Ta có: \[\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{\left( {{x^2} - 4} \right)\left( {\sqrt {2f\left( x \right) + 6} + 3} \right)}}\]\[ = \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 15}}{{\left( {x - 2} \right)\left( {x + 2} \right)\left( {\sqrt {2f\left( x \right) + 6} + 3} \right)}}\]
\[ = \mathop {\lim }\limits_{x \to 2} \left[ {\frac{{f\left( x \right) - 15}}{{x - 2}} \cdot \frac{1}{{\left( {x + 2} \right)\left( {\sqrt {2f\left( x \right) + 6} + 3} \right)}}} \right]\]\[ = 3 \cdot \frac{1}{{4 \cdot \left( {\sqrt {2 \cdot 15 + 6} + 3} \right)}} = 3 \cdot \frac{1}{{4 \cdot 9}} = \frac{1}{{12}}\].
Đáp án: \[\frac{1}{{12}}\].
Câu 41:
Ký hiệu \[M\] và \[m\] tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^2} - 2x + 5\) trên miền \[\left[ {2\,;\,\,7} \right].\] Khi đó \(M\) gấp \(m\) bao nhiêu lần?
Đáp án: ……….
 Xem đáp án
Xem đáp án
Xét hà\(y = {x^2} - 2x + 5\)m số \(y = {x^2} - 2x + 5\) trên \(\left[ {2\,;{\mkern 1mu} {\mkern 1mu} 7} \right]\) ta có bảng biến thiên:
Đỉnh của đồ thị hàm số là \(I\left( {1\,;{\mkern 1mu} {\mkern 1mu} \,4} \right)\).
![Ký hiệu \[M\] và \[m\] tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^2} - 2x + 5\) trên miền \[\left[ {2\,;\,\,7} \right].\] Khi đó \(M\) gấp \(m\) bao nhiêu lần? Đáp án: ………. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/08/blobid10-1722739571.png)
Dựa vào bảng biến thiên, ta có: \(M = \mathop {\max }\limits_{\left[ {2;{\kern 1pt} {\kern 1pt} 7} \right]} y = 40\) khi \(x = 7\) và \(m = \mathop {\min }\limits_{\left[ {2;{\kern 1pt} {\kern 1pt} 7} \right]} y = 5\) khi \(x = 2\).
Do đó \(M = 8m\).
Đáp án: 8.
Câu 42:
Cho hàm số \(y = m{x^4} + \left( {m - 1} \right){x^2} + 1 - 2m\). Tất cả giá trị nào của \(m\) thì hàm số đã cho chỉ có một cực trị thì \(m \le a\) và \(m \ge b\). Khi đó \(b - a\) bằng
Đáp án: ……….
 Xem đáp án
Xem đáp án
Ta có \(y' = 4m{x^3} + 2\left( {m - 1} \right)x = 2x\left( {2m{x^2} + m - 1} \right)\); \(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{2m{x^2} + m - 1 = 0{\mkern 1mu} {\mkern 1mu} \,\left( 1 \right)}\end{array}} \right.\)
Hàm số chỉ có 1 cực trị \( \Leftrightarrow \left( 1 \right)\) vô nghiệm hoặc có nghiệm kép
\( \Rightarrow \Delta \le 0 \Leftrightarrow - 2m\left( {m - 1} \right) \le 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \le 0}\\{m \ge 1}\end{array}} \right.\). Khi đó \(a = 0\,;\,\,b = 1\) nên \(b - a = 1.\)
Đáp án: 1.
Câu 43:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 4x + 3\), trục hoành và hai đường thẳng \(x = 1,{\mkern 1mu} {\mkern 1mu} \,x = 2\) bằng
Đáp án: ……….
 Xem đáp án
Xem đáp án
Diện tích cần tìm là: \(S = \int\limits_1^2 {\left| {{x^2} - 4x + 3} \right|dx} = \int\limits_1^2 {\left( { - {x^2} + 4x - 3} \right)dx} \)
\({\mkern 1mu} = \int\limits_1^2 { - {x^2}dx + \int\limits_1^2 {4xdx} } - \int\limits_1^2 {3dx} \)\( = \left. { - \frac{{{x^3}}}{3}} \right|_1^2 + \left. {2{x^2}} \right|_1^2 - \left. {3x} \right|_1^2\)\({\mkern 1mu} = - \frac{8}{3} + \frac{1}{3} + 8 - 2 - 6 + 3 = \frac{2}{3}\).
Đáp án: \(\frac{2}{3}\).
Câu 44:
![Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Giá trị của \[m\] để phương trình \[f\left( {\sin x} \right) = m\] có đúng hai nghiệm trên đoạn \[\left[ {0\,;\,\,\pi } \right]\] và \[m \in \left( {a\,;\,\,b} \right]\] thì \(a + b\) bằng Đáp án: ………. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/08/blobid11-1722739728.png)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Giá trị của \[m\] để phương trình \[f\left( {\sin x} \right) = m\] có đúng hai nghiệm trên đoạn \[\left[ {0\,;\,\,\pi } \right]\] và \[m \in \left( {a\,;\,\,b} \right]\] thì \(a + b\) bằng
Đáp án: ………. Xem đáp án
Xem đáp án
Đặt \[t = \sin x \in \left[ { - 1\,;\,1} \right]\].
Dễ thấy với mỗi \[t \in \left[ {0;1} \right)\] thì sẽ có 2 giá trị \[x \in \left[ {0;\pi } \right]\].
Do đó, để phương trình đã cho có đúng hai nghiệm trên đoạn \[\left[ {0;\pi } \right]\] thì phương trình \[f\left( t \right) = m\] có nghiệm duy nhất t \[t \in \left[ {0;1} \right)\]\[ \Leftrightarrow - 4 < m \le - 3\].
Đáp án: −7.
Câu 45:
Đáp án: ……….
 Xem đáp án
Xem đáp án
Đặt \(z = x + yi{\mkern 1mu} \,{\mkern 1mu} \left( {x,\,y \in \mathbb{R}} \right)\).
Theo bài ra ta có: \(\left| {x + yi - 2 + i} \right| = 4 \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 16\).
Vậy tập hợp các điểm biểu diễn các số phức \(z\) là một đường tròn có tâm \(I\left( {2;1} \right)\), bán kính \(R = 4\)Đáp án: 4.
Câu 46:
Cho lăng trụ đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \[a.\] Gọi \(\alpha \) là góc giữa mặt phẳng \(\left( {A'BC} \right)\) và mặt phẳng \(\left( {ABC} \right)\). Tính \(\tan \alpha \).
Đáp án: ……….
 Xem đáp án
Xem đáp án
![Cho lăng trụ đều \(ABC.A'B'C'\) có tất cả các cạnh bằng \[a.\] Gọi \(\alpha \) là góc giữa mặt phẳng \(\left( {A'BC} \right)\) và mặt phẳng \(\left( {ABC} \right)\). Tính \(\tan \alpha \). Đáp án: ………. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/08/blobid12-1722739823.png)
Gọi \(I\) là trung điểm của \(BC\).
Vì \(\Delta ABC\) đều nên \(AI \bot BC\) và \(AI = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{BC \bot AI}\\{BC \bot AA'}\end{array}} \right. \Rightarrow BC \bot \left( {AIA'} \right) \Rightarrow BC \bot A'I\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\left( {ABC} \right) \cap \left( {A'BC} \right) = BC}\\{AI \subset \left( {ABC} \right),{\mkern 1mu} \,AI \bot BC}\\{A'I \subset \left( {ABC} \right),{\mkern 1mu} \,A'I \bot BC}\end{array}} \right.\)\( \Rightarrow \alpha = \widehat {\left( {\left( {ABC} \right),\left( {A'BC} \right)} \right)} = \widehat {AIA'}\)
Xét tam giác vuông \(AIA'\) ta có: \(\tan \alpha = \frac{{AA'}}{{AI}} = \frac{a}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{2\sqrt 3 }}{3}\).
Đáp án: \(\frac{{2\sqrt 3 }}{3}\)
Câu 47:
Trong không gian với hệ tọa độ \[Oxyz,\] điểm \(A'\) đối xứng với điểm \(A\left( { - 1\,;\,\,0\,;\,\,3} \right)\) qua mặt phẳng \(\left( P \right):x + 3y - 2z - 7 = 0\). Khi đó, hoành độ của điểm \(A'\) là
Đáp án: ……….
 Xem đáp án
Xem đáp án
Giả sử \[A'\left( {a\,;\,\,b\,;\,\,c} \right)\] là điểm đối xứng với điểm \[A\left( { - 1\,;\,\,0\,;\,\,3} \right)\] qua mặt phẳng \[\left( P \right):x + 3y - 2z - 7 = 0\]
Khi đó, ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AA'} \,{\rm{//}}\,\overrightarrow {{n_{\left( P \right)}}} }\\{I \in \left( P \right)}\end{array}} \right.\), với \[I\] là trung điểm của \[{\rm{AA'}}\].
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{a + 1}}{1} = \frac{{b - 0}}{3} = \frac{{c - 3}}{{ - 2}}}\\{\left( {\frac{{a - 1}}{2}} \right) + 3.\frac{b}{2} - 2.\frac{{c + 3}}{2} - 7 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{a + 1}}{1} = \frac{b}{3} = \frac{{c - 3}}{{ - 2}}}\\{a + 3b - 2c = 21}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 6}\\{c = - 1}\end{array}} \right.\)\( \Rightarrow A'\left( {1;6; - 1} \right)\). Do đó, hoành độ của điểm \(A'\) là 1.
Đáp án: 1.
Câu 48:
Xét các số thực \(x,y\) thỏa mãn \({2^{{x^2} + {y^2} + 1}} \le \left( {{x^2} + {y^2} - 2x + 2} \right){4^x}\). Giá trị lớn nhất của biểu thức \(P = \frac{{8x + 4}}{{2x - y + 1}}\) gần nhất với số nào dưới đây?
Đáp án: ……….
 Xem đáp án
Xem đáp án
Nhận xét: \({x^2} + {y^2} - 2x + 2 = {\left( {x - 1} \right)^2} + {y^2} + 1 > 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x,y\)
Bpt \( \Leftrightarrow {2^{{x^2} + {y^2} - 2x + 1}} \le {x^2} + {y^2} - 2x + 2\)
Đặt \(t = {x^2} + {y^2} - 2x + 1\), bất phương trình trở thành \({2^t} \le t + 1 \Leftrightarrow {2^t} - t - 1 \le 0\)
Xét hàm số \(f\left( t \right) = {2^t} - t - 1\) có \(f'\left( t \right) = {2^t}\ln 2 - 1 = 0 \Leftrightarrow t = {\log _2}\left( {{{\log }_2}e} \right).\)
Ta có bảng biến thiên:
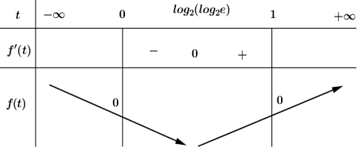
Suy ra ta có \(0 \le t \le 1 \Rightarrow {\left( {x - 1} \right)^2} + {y^2} \le 1\)
Ta có: \(P = \frac{{8x + 4}}{{2x - y + 1}}\)\[ \Leftrightarrow 2Px - Py + P = 8x + 4\]
\[ \Leftrightarrow P - 4 = \left( {8 - 2P} \right)x + Py\]\[ \Leftrightarrow 3P - 12 = \left( {8 - 2P} \right)\left( {x - 1} \right) + Py\]
\[ \Leftrightarrow {\left( {3P - 12} \right)^2} \le \left[ {{{\left( {8 - 2P} \right)}^2} + {P^2}} \right]\left[ {{{\left( {x - 1} \right)}^2} + {y^2}} \right]\]\[ \Rightarrow {\left( {3P - 12} \right)^2} \le {\left( {8 - 2P} \right)^2} + {P^2}\]
\[ \Leftrightarrow 4{P^2} - 40P + 80 \le 0\]\[ \Leftrightarrow 5 - \sqrt 5 \le P \le 5 + \sqrt 5 \approx 7,23\].
Dấu xảy ra \[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{8 - 2P}}{P} = \frac{{x - 1}}{y} = - \frac{2}{{\sqrt 5 }}}\\{{{\left( {x - 1} \right)}^2} + {y^2} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x - 1 = - \frac{2}{{\sqrt 5 }}y}\\{\frac{9}{5}{y^2} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1 \mp \frac{2}{3}}\\{y = \pm \frac{{\sqrt 5 }}{3}}\end{array}} \right.\].
Do đó \[\max P = 5 + \sqrt 5 \] đạt được khi \[x = \frac{1}{3}\,;\,\,y = \frac{{\sqrt 5 }}{3}\]. Đáp án: 7.
Câu 49:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh\(y = {x^2} - 2x + 5\)\(2a\), tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(\varphi \) và \(\sin \varphi = \frac{{\sqrt 5 }}{5}\). Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\) bằng
Đáp án: ……….
 Xem đáp án
Xem đáp án
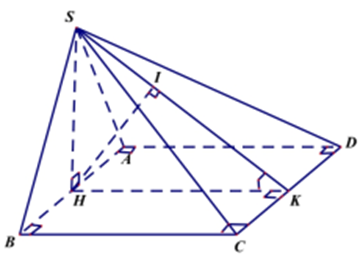
Gọi \(H\) là trung điểm của \(AB\). Vì tam giác \(SAB\) cân tại \(S\) nên \(SH \bot AB\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SAB} \right) \bot \left( {ABCD} \right) = AB}\\{SH \subset \left( {SAB} \right),{\mkern 1mu} {\mkern 1mu} SH \bot AB}\end{array}} \right. \Rightarrow SH \bot \left( {ABCD} \right)\)
Gọi \(K\) là trung điểm của \(CD\) ta có
\(\left\{ {\begin{array}{*{20}{l}}{CD \bot HK}\\{CD \bot SH}\end{array}} \right. \Rightarrow CD \bot \left( {SHK} \right) \Rightarrow CD \bot SK\)
\(\left\{ {\begin{array}{*{20}{l}}{\left( {SCD} \right) \cap \left( {ABCD} \right) = CD}\\{SK \subset \left( {SCD} \right),{\mkern 1mu} {\mkern 1mu} \,SK \bot CD}\\{HK \subset \left( {ABCD} \right),{\mkern 1mu} {\mkern 1mu} \,HK \bot CD}\end{array}} \right.\)\( \Rightarrow \widehat {\left( {\left( {SCD} \right),\left( {ABCD} \right)} \right)} = \widehat {\left( {SK,HK} \right)} = \widehat {SKH} = \varphi \)
Vì \(AH\,{\rm{//}}\,CD \Rightarrow AH\,{\rm{//}}\,\left( {SCD} \right) \Rightarrow d\left( {A,\left( {SCD} \right)} \right) = d\left( {H,\left( {SCD} \right)} \right)\)
Trong \(\left( {SHK} \right)\) kẻ \(HI \bot SK{\mkern 1mu} {\mkern 1mu} \left( {I \in SK} \right)\) ta có: \(\left\{ {\begin{array}{*{20}{l}}{HI \bot SK}\\{HI \bot CD{\mkern 1mu} {\mkern 1mu} \left( {CD \bot \left( {SHK} \right)} \right)}\end{array}} \right. \Rightarrow HI \bot \left( {SCD} \right)\)
\( \Rightarrow d\left( {H,\left( {SCD} \right)} \right) = HI\).
Xét tam giác vuông \(HIK\) ta có \(\sin \varphi = \sin \widehat {SKH} = \frac{{HI}}{{HK}}\) \( \Rightarrow HI = HK.\sin \varphi = 2a.\frac{{\sqrt 5 }}{5} = \frac{{2a\sqrt 5 }}{5}\)
Vậy \(d\left( {A,\left( {SCD} \right)} \right) = \frac{{2a\sqrt 5 }}{5}\). Đáp án: \(\frac{{2\sqrt 5 a}}{5}\).
Câu 50:
Ông \(A\) dự định sử dụng hết \(6,5\,\,{m^3}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Đáp án: ……….
 Xem đáp án
Xem đáp án
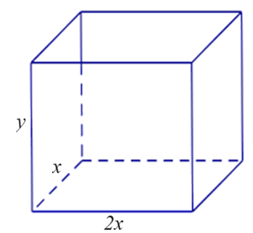
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,\,2x,\,\,y\,\,\left( {x,\,\,y > 0} \right)\).
Diện tích phần lắp kính là: \(2x.x + 2xy + 2.2x.y = 2{x^2} + 6xy = 6,5\)
\( \Leftrightarrow xy = \frac{{6,5 - 2{x^2}}}{6} > 0 \Rightarrow x < \sqrt {\frac{{6,5}}{2}} = \frac{{\sqrt {13} }}{2}.\)
Thể tích bể cá là: \(V = 2x \cdot x \cdot y = 2x \cdot \frac{{6,5 - 2{x^2}}}{6} = \frac{{ - 4{x^3} + 13x}}{6}\) với \(0 < x < \frac{{\sqrt {13} }}{2}\).
Ta có \(V' = \frac{{ - 12{x^2} + 13}}{6},V' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{\sqrt {39} }}{6}}\\{x = - \frac{{\sqrt {39} }}{6}\left( L \right)}\end{array}} \right.\)
Bảng biến thiên:
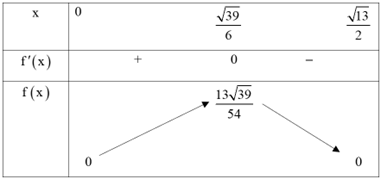
Vậy \[{V_{\max }} = \frac{{13\sqrt {39} }}{{54}} \approx 1,5\,{\mkern 1mu} \,\left( {{m^3}} \right)\].
Đáp án:\(1,5\).
Câu 51:
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Từ “bừng” trong câu thơ thứ (1) diễn tả cảm xúc ngỡ ngàng, bất ngờ. Chọn C.
Câu 52:
 Xem đáp án
Xem đáp án
Nếu cảnh một đêm liên hoan đem đến cho người đọc không khí mê say, ngây ngất, thì cảnh sông nước miền Tây lại gợi lên được cảm giác mênh mang, mờ ảo. Chọn C.
Câu 53:
 Xem đáp án
Xem đáp án
Nội dung chính: Nỗi nhớ những kỉ niệm đẹp về tình quân dân trong đêm liên hoan văn nghệ và cảnh sông nước miền Tây. Chọn A.
Câu 54:
 Xem đáp án
Xem đáp án
Trong đoạn trích có 2 từ láy là: “e ấp” và “đong đưa”. Chọn B.
Câu 55:
 Xem đáp án
Xem đáp án
Câu 56:
 Xem đáp án
Xem đáp án
Phương thức biểu đạt chính: Tự sự. Chọn B.
Câu 57:
 Xem đáp án
Xem đáp án
Tâm trạng của bà cụ Tứ trong đoạn trích trên là tâm trạng xót thương, ai oán. Để lí giải điều này có thể căn cứ vào câu văn thứ 3 của đoạn trích: Lòng người mẹ nghèo khổ ấy còn hiểu ra biết bao nhiêu cơ sự, vừa ai oán vừa xót thương cho số kiếp đứa con mình. Chọn A.
Câu 58:
 Xem đáp án
Xem đáp án
Từ “cơ sự” gần nghĩa hơn cả với từ “sự tình”. Chọn B.
Câu 59:
 Xem đáp án
Xem đáp án
Nhân vật bà cụ Tứ trong đoạn trích là người mẹ thương con và giàu lòng nhân ái. Chọn B.
Câu 60:
 Xem đáp án
Xem đáp án
Dấu ba chấm được tác giả sử dụng trong câu văn “Còn mình thì...” thể hiện sự ngừng lặng trong lời độc thoại nội tâm của nhân vật bà cụ Tứ khi bà so sánh hoàn cảnh gia đình mình và hoàn cảnh gia đình người ta. Để lí giải cho lựa chọn này có thể xuất phát từ một trong những chức năng của dấu ba chấm là dùng để thể hiện chỗ lời nói còn bỏ dở hay ngập ngừng, ngắt quãng. Chọn C.
Câu 61:
 Xem đáp án
Xem đáp án
Phương thức biểu đạt chính: tự sự. Chọn C.
Câu 62:
 Xem đáp án
Xem đáp án
Nhan đề “Hai hạt lúa” là bao quát nhất cho văn bản trên. Chọn A.
Câu 63:
 Xem đáp án
Xem đáp án
Hạt lúa thứ hai thật sự sung sướng khi được bắt đầu một cuộc đời mới. Chọn B.
Câu 64:
 Xem đáp án
Xem đáp án
Đoạn trích sử dụng biện pháp tu từ nhân hóa – hạt lúa có suy nghĩ, tiếng nói giống như con người. Chọn D.
Câu 65:
 Xem đáp án
Xem đáp án
Văn bản mượn hình ảnh hai hạt lúa để nói về lối sống của con người. Từ đó rút ra thông điệp cần biết chấp nhận thử thách để sống ý nghĩa. Chọn B.
Câu 66:
 Xem đáp án
Xem đáp án
Câu 67:
 Xem đáp án
Xem đáp án
Dựa vào câu văn: Với một đứa trẻ, để dạy chúng “tự lái”, cha mẹ nên biết tạo áp lực vừa phải, đủ giúp chúng kiểm soát tốt bản thân và để cha mẹ hiểu tâm sinh lí, khả năng của con nhằm đồng hành với chúng. Cha mẹ cần tạo áp lực vừa phải để trẻ có khả năng kiểm soát bản thân. Chọn D.
Câu 68:
 Xem đáp án
Xem đáp án
Áp lực độc lại là áp lực vượt quá khả năng chịu đựng của con người gây nên những tổn thương về mặt tâm lí. Chọn B.
Câu 69:
 Xem đáp án
Xem đáp án
Từ “tự lái” ẩn ý nói đến việc đứa trẻ biết tự giải quyết những khó khăn, áp lực xảy ra trong cuộc sống. Chọn B.
Câu 70:
 Xem đáp án
Xem đáp án
Dựa vào câu văn cuối cùng: Với một đứa trẻ, để dạy chúng “tự lái”, cha mẹ nên biết tạo áp lực vừa phải, đủ giúp chúng kiểm soát tốt bản thân và để cha mẹ hiểu tâm sinh lí, khả năng của con nhằm đồng hành với chúng. Chọn D.
Câu 71:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Anh Hoàng là người cán bộ độc nhất mà ông tin cậy.
 Xem đáp án
Xem đáp án
Từ “độc nhất” dùng sai về ngữ nghĩa. Từ đúng là “duy nhất”. Chọn C.
Câu 72:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Lan chăm chú nghe ngóng ý kiến của thẩm phán và các luật sư bào chữa.
 Xem đáp án
Xem đáp án
Từ dùng sai là “nghe ngóng”: lắng nghe (tin tức, dư luận) xem sao (để qua đó quyết định hành động của mình). Nên thay bằng “lắng nghe”. Chọn B.
Câu 73:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Tìm thêm các ví dụ trong thơ Nôm của Nguyễn Trãi, Hồ Xuân Hương, Truyện Kiều... để chứng minh rằng: từ thế kỉ XV trở đi, tiếng Việt đã đạt đến mức độ tinh tế, uyển chuyển.
 Xem đáp án
Xem đáp án
“Truyện Kiều” là tên tác phẩm, không tương hợp với các tên riêng chỉ tác giả trong câu. Chọn C.
Câu 74:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Trong hoàn cảnh éo le ấy, chị cảm thấy bất lực và kiệt sức, định buông thả cho số phận.
 Xem đáp án
Xem đáp án
Từ dùng sai là “buông thả” (thả lỏng hoàn toàn, để cho tự do, không giữ gìn, hạn chế). Nên thay bằng “buông xuôi” (bỏ mặc không can thiệp đến, để cho sự việc tiếp tục diễn biến theo chiều hướng xấu). Chọn D.
Câu 75:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Những lời nói chân tình từ đáy lòng khiến mọi người rất cảm xúc.
 Xem đáp án
Xem đáp án
Sau từ “rất” thường là tính từ. Từ “cảm xúc” dùng sai. Nên thay bằng “xúc động”. Chọn D.
Câu 76:
 Xem đáp án
Xem đáp án
“Tàu thuyền” chỉ các loại phương tiện giao thông đường thủy nói chung. Các từ còn lại chỉ các loại thuyền cụ thể. Chọn B.
Câu 77:
 Xem đáp án
Xem đáp án
Từ “lưỡi” trong “tặc lưỡi” dùng với nghĩa gốc, các từ còn lại dùng với nghĩa chuyển. Chọn A.
Câu 78:
 Xem đáp án
Xem đáp án
“Lèm nhèm” chỉ đặc điểm không được sạch sẽ, rõ ràng, minh bạch của hành động. Các từ còn lại chỉ lời nói của con người. Chọn C.
Câu 79:
 Xem đáp án
Xem đáp án
Từ “gia” trong “gia vị” là thêm vào, trong các từ còn lại (gia súc, gia dụng, gia chủ) lại có nghĩa là nhà. Chọn D.
Câu 80:
 Xem đáp án
Xem đáp án
Từ “học tập” là động từ, các từ còn lại đều là danh từ. Chọn D.
Câu 81:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Nghe bệnh, bắt mạch xong, ông _________ kê đơn bốc thuốc.
 Xem đáp án
Xem đáp án
Nghe bệnh, bắt mạch xong, ông thận trọng kê đơn bốc thuốc. Chọn C.
Câu 82:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Văn bản mới của Bộ Giáo dục và Đào tạo cho thấy ________ tuyển sinh năm nay đã tăng đáng kể.
 Xem đáp án
Xem đáp án
Văn bản mới của Bộ Giáo dục và Đào tạo cho thấy chỉ tiêu tuyển sinh năm nay đã tăng đáng kể. Chọn B.
Câu 83:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Dù nhảy xuống sông cũng cứ phải bám chặt vào phao thì mới mong ________ mạng sống.
 Xem đáp án
Xem đáp án
“Bảo toàn” là giữ cho nguyên vẹn, “bảo tồn” là giữ cho không bị mất đi, “bảo vệ” là chống lại mọi sự xâm phạm và bênh vực bằng lí lẽ, “bảo đảm” là làm cho chắc chắn thực hiện được, chịu trách nhiệm về lời nói của mình. Từ thích hợp nhất với “mạng sống” là “bảo toàn”. Chọn C.
Câu 84:
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Đà Lạt là điểm du lịch tuyệt vời và là nơi lí tưởng để _________ tinh thần sau thời gian làm việc căng thẳng.
 Xem đáp án
Xem đáp án
“Di dưỡng”: bồi bổ, tạo điều kiện cho có được sự phát triển tốt, khắc phục sự suy sút có thể có (thường nói về mặt tinh thần). Chọn B.
Câu 85:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Cơ quan anh Hoàng vừa ________ 2 phòng ấy thành “Phòng tổng hợp”.
 Xem đáp án
Xem đáp án
“sáp nhập”: nhập vào với nhau làm một (thường nói về các tổ chức, đơn vị hành chính). Chọn B.
Câu 86:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Mỗi tháng, y vẫn cho nó dăm hào. Khi sai nó trả tiền giặt hay mua thức gì, còn năm ba xu, một vài hào, y thường cho nốt nó luôn. Nhưng cho rồi, y vẫn thường tiếc ngấm ngầm. Bởi vì những số tiền cho lặt vặt ấy, góp lại, trong một tháng, có thể thành đến hàng đồng.
(Sống mòn – Nam Cao)
 Xem đáp án
Xem đáp án
Câu 87:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tại cuộc họp nóng chiều 31/1, trước cơn sốt khẩu trang y tế tăng giá gấp nhiều lần, khan hiếm hàng, Bộ Y tế cho biết: Hiện dịch chưa lây lan mạnh mẽ trong cộng đồng thì khi đến những chỗ nguy cơ cao như đi phương tiện công cộng, đến bệnh viện có thể dùng khẩu trang y tế thông thường, thậm chí có thể dùng khẩu trang vải.
(Sưu tầm)
 Xem đáp án
Xem đáp án
“Cơn sốt” có ý nghĩa chỉ quá trình tăng mạnh một cách đột biến, nhất thời về giá cả hoặc nhu cầu nào đó trong xã hội. Chọn A.
Câu 88:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Biết quý công cầm vàng những ngày lặn lội
Biết trồng tre đợi ngày thành gậy
Đi trả thù mà không sợ dài lâu
Ôi những dòng sông bắt nước từ đâu
Mà khi về Đất Nước mình thì bắt lên câu hát
Người đến hát khi chèo đò, kéo thuyền vượt thác
Gợi trăm màu trên trăm dáng sông xuôi.
(Đất nước – Nguyễn Khoa Điềm)
 Xem đáp án
Xem đáp án
Câu “Biết quý công cầm vàng những ngày lặn lội” lấy ý từ câu ca dao: “Cầm vàng mà lội qua sông/ Vàng rơi không tiếc, tiếc công cầm vàng”. Chọn B.
Câu 89:
Đọc đoạn trích sau và trả lời câu hỏi:
Hồn Trương Ba: Sống nhờ vào đồ đạc, của cải người khác, đã là chuyện không nên, đằng này đến cái thân tôi cũng phải sống nhờ anh hàng thịt. Ông chỉ nghĩ đơn giản là cho tôi sống, nhưng sống như thế nào thì ông chẳng cần biết.
Đế Thích (không hiểu): Nhưng mà ông muốn gì?
(Hồn Trương Ba da hàng thịt – Lưu Quang Vũ)
 Xem đáp án
Xem đáp án
Đoạn trích thể hiện ý thức sâu sắc của Trương Ba: Khi phải sống nhờ, sống gửi, sống chắp vá, không được là mình thì cuộc sống thật vô nghĩa. Chọn D.
Câu 90:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Làm trai cho đáng nên trai,
Kéo đũa cho dài ăn vụng cơm con.
(Ca dao)
 Xem đáp án
Xem đáp án
Bài ca dao trên mang giọng điệu giễu cợt, châm chọc người đàn ông lười biếng, ham ăn. Chọn D.
Câu 91:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Chị Hai là con nuôi của má. Cha mẹ chị cũng vì một tay thằng Tây mà chết. Hồi ba dắt về trao cho má, chị mới chín tuổi, ốm nhom, một mảng tóc bị bom xăng làm cháy còn sém như đuôi bò. Chị lớn tuổi hơn chị Chiến nên má đặt chị là chị thứ hai... Rồi chị lớn lên, lấy chồng, công tác luôn dưới đó. Sau này, mỗi năm đôi ba lần, chị lại vượt cánh đồng mấy chục cây số, lội qua mấy chục đồn bót giặc về thăm má, thăm em. Trừ mắc công tác thì thôi, còn thì trời sập chị cũng về. Cứ một mình ôm nón mà đi.
(Những đứa con trong gia đình – Nguyễn Thi)
 Xem đáp án
Xem đáp án
Dựa vào chi tiết: Sau này, mỗi năm đôi ba lần, chị lại vượt cánh đồng mấy chục cây số, lội qua mấy chục đồn bót giặc về thăm má, thăm em. Trừ mắc công tác thì thôi, còn thì trời sập chị cũng về. Cứ một mình ôm nón mà đi,… cho thấy nhân vật “chị Hai” rất hiếu thảo, dũng cảm. Chọn D.
Câu 92:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Gió theo lối gió mây đường mây
Dòng nước buồn thiu hoa bắp lay
Thuyền ai đậu bến sông trăng đó
Có chở trăng về kịp tối nay?
(Đây thôn Vĩ Dạ – Hàn Mặc Tử)
 Xem đáp án
Xem đáp án
Đoạn thơ gợi nỗi buồn chia lìa, xa cách: Gió theo lối gió mây đường mây, Dòng nước buồn thiu hoa bắp lay. Chọn B.
Câu 93:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Nhiều đồng bào chúng ta, để biện minh cho việc từ bỏ tiếng mẹ đẻ, đã than phiền rằng tiếng nước mình nghèo nàn. Lời trách cứ này không có cơ sở nào cả. Họ chỉ biết những từ thông dụng của ngôn ngữ và còn nghèo những từ An Nam hơn bất cứ người phụ nữ và nông dân An Nam nào. Ngôn ngữ của Nguyễn Du nghèo hay giàu?
Vì sao người An Nam có thể dịch những tác phẩm của Trung Quốc sang nước mình, mà lại không thể viết những tác phẩm tương tự?
Phải quy lỗi cho sự nghèo nàn của ngôn ngữ hay sự bất tài của con người?
(Tiếng mẹ đẻ - nguồn giải phóng các dân tộc bị áp bức – Nguyễn An Ninh)
 Xem đáp án
Xem đáp án
Nội dung chính: Khẳng định tiếng mẹ đẻ giàu có. Chọn B.
Câu 94:
Đọc đoạn trích sau và trả lời câu hỏi:
Người đàn bà như cũng biết xung quanh người ta đang nhìn dồn cả về phía mình, thị càng ngượng nghịu, chân nọ bước díu cả vào chân kia.
(Vợ nhặt – Kim Lân)
 Xem đáp án
Xem đáp án
Câu văn khắc họa tâm trạng xấu hổ của thị trên đường về nhà Tràng. Chọn B.
Câu 95:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Cái đẹp vừa là xinh, là khéo. Ta không háo hức cái tráng lệ, huy hoàng, không say mê cái huyền ảo, kì vĩ. Màu sắc chuộng cái dịu dàng, thanh nhã, ghét sặc sỡ. Quy mô chuộng sự vừa khéo vừa xinh, phải khoảng. Giao tiếp ứng xử chuộng hợp tình, hợp lí, áo quần, trang sức, món ăn đều không chuộng sự cầu kì. Tất cả đều hướng vào cái đẹp dịu dàng, thanh lịch, duyên dáng có quy mô vừa phải.
(Nhìn về văn hóa dân tộc – Trần Đình Hượu)
 Xem đáp án
Xem đáp án
Nội dung chính: Cái đẹp là cái có chừng mực và quy mô vừa phải. Chọn C.
Câu 96:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Vũ Như Tô – Có việc gì mà bà chạy hớt hơ hớt hải? Mặt bà cắt không còn hột máu.
Đan Thiềm (thở hổn hển) – Nguy đến nơi rồi... Ông Cả!
Vũ Như Tô – Lạ chưa, nguy làm sao? Đài Cửu Trùng chia năm đã được một phần.
Đan Thiềm – Ông trốn đi, mau lên không thì không kịp.
Vũ Như Tô – Sao bà nói lạ? Đài Cửu Trùng chưa xong, tôi trốn đi đâu. Làm gì phải trốn?
Đan Thiềm – Ông nghe tôi! Ông trốn đi! Ông nghe tôi! Ông phải trốn đi mới được!
Vũ Như Tô – Làm sao tôi cần phải trốn? Bà nói rõ cho là vì sao? Khi trước tôi nhờ bà mách đường chạy trốn, bà khuyên không nên, bây giờ bà bảo tôi đi trốn, thế là nghĩa gì?
Đan Thiềm – Có nghĩa lắm. Tôi không làm một việc gì vô lí cả. Khi trước trốn đi thì ông nguy, bây giờ trốn đi thì ông thoát chết.
(Vĩnh biệt Cửu Trùng Đài, Trích Vũ Như Tô – Nguyễn Huy Tưởng)
 Xem đáp án
Xem đáp án
Lời thoại của nhân vật gây kịch tính, căng thẳng. Chọn D.
Câu 97:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Đất nước
Của những dòng sông
Gọi tên nghe mát rượi tâm hồn
Ngọt lịm, những giọng hò xứ sở
Trong sáng như trời xanh, mượt mà như nhung lụa.
(Chúng con chiến đấu, Nam Hà)
 Xem đáp án
Xem đáp án
Đoạn thơ viết theo thể tự do. Số câu, số chữ, ngắt nhịp,… linh hoạt. Chọn B.
Câu 98:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Ngày thứ nhất – ai biết đích ngày nào – chữ tôi xuất hiện trên thi đàn Việt Nam, nó thực bỡ ngỡ. Nó như lạc loài nơi đất khách. Bởi nó mang theo một quan niệm chưa từng thấy ở xứ này: quan niệm cá nhân. Xã hội Việt Nam từ xưa không có cá nhân. Chỉ có đoàn thể: lớn thì quốc gia, nhỏ thì gia đình. Còn cá nhân, cái bản sắc của cá nhân chìm đắm trong gia đình, trong quốc gia như giọt nước trong biển cả. Cũng có những bậc kì tài xuất đầu lộ diện. Thảng hoặc họ cũng ghi hình ảnh họ trong văn thơ. Và thảng hoặc trong văn thơ họ cũng dùng đến chữ tôi để nói chuyện với người khác. Song dầu táo bạo đến đâu họ cũng không một lần nào dám dùng chữ tôi để nói chuyện với mình, hay – thì cũng thế – với tất cả mọi người.
(Một thời đại trong thi ca – Hoài Thanh)
 Xem đáp án
Xem đáp án
Thao tác lập luận chính của đoạn trích là chứng minh. Hoài Thanh đưa ra luận điểm trong câu văn đầu tiên: Ngày thứ nhất - ai biết đích ngày nào - chữ tôi xuất hiện trên thi đàn Việt Nam, nó thực bỡ ngỡ. Sau đó, tác giả dùng các lí lẽ (Nó như lạc loài nơi đất khách. Bởi nó mang theo một quan niệm chưa từng thấy ở xứ này: quan niệm cá nhân. Xã hội Việt Nam từ xưa không có cá nhân. Chỉ có đoàn thể: lớn thì quốc gia, nhỏ thì gia đình. Còn cá nhân, cái bản sắc của cá nhân chìm đắm trong gia đình, trong quốc gia như giọt nước trong biển cả, ...) để chứng minh cho luận điểm đó. Chọn B.
Câu 99:
Đọc đoạn trích sau và trả lời câu hỏi:
Chớ tự kiêu, tự đại. Tự kiêu, tự đại là khờ dại. Vì mình hay, còn nhiều người hay hơn mình. Mình giỏi, còn nhiều người giỏi hơn mình. Tự kiêu, tự đại tức là thoái bộ. Sông to, biển rộng, thì bao nhiêu nước cũng chứa được, vì độ lượng nó rộng và sâu. Cái chén nhỏ, cái đĩa cạn, thì một chút nước cũng đầy tràn, vì độ lượng nó hẹp nhỏ. Người mà tự kiêu, tự mãn, cũng như cái chén, cái đĩa cạn…
(Trích Cần kiệm liêm chính, Hồ Chí Minh, tháng 6-1949)
 Xem đáp án
Xem đáp án
Đoạn trích trên mang đầy đủ đặc điểm của phong cách chính luận:
- Tính công khai về quan điểm chính trị: Tác giả bày tỏ quan điểm của mình về tính tự kiêu, tự đại và tác hại của nó đối với con người.
- Tính chặt chẽ trong diễn đạt và suy luận: Tác giả đưa ra tác hại của tính tự kiêu và lấy ví dụ so sánh để người đọc có thể hình dung một cách cụ thể. Các câu văn ngắn liên tiếp được nối với nhau bằng các phép liên kết câu làm cho đoạn văn trở nên chặt chẽ.
- Tính truyền cảm và thuyết phục: Giọng điệu hùng hồn, ngôn từ sáng rõ.
→ Chọn C.
Câu 100:
Đọc đoạn trích sau đây và trả lời câu hỏi:
đường chỉ tay đã đứt
dòng sông rộng vô cùng
Lor-ca bơi sang ngang
trên chiếc ghi ta màu bạc
chàng ném lá bùa cô gái Di-gan
vào xoáy nước
chàng ném trái tim mình
vào lặng yên bất chợt
li-la li-la li-la...
(Đàn ghi ta của Lor-ca – Thanh Thảo)
 Xem đáp án
Xem đáp án
Cả đoạn trích là nối tiếp những câu thơ không viết hoa các chữ cái đầu câu, có thể coi đó là những cảm nhận mơ hồ, những liên tưởng đột ngột, những ấn tượng bất chợt của phong cách thơ siêu thực, tượng trưng của cả bài thơ. Chọn C.
Câu 101:
PHẦN 3: KHOA HỌC
Lĩnh vực: Khoa học tự nhiên và xã hội (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Chiến tranh đặc biệt không có sự tham gia của quân Mĩ và quân đồng minh Mĩ. Đến Chiến tranh cục bộ quân viễn chinh Mĩ và quân đồng minh Mĩ đã trực tiếp tham chiến và giữ vai trò quan trọng và không ngừng tăng lên về số lượng. Chọn A.
Câu 102:
 Xem đáp án
Xem đáp án
Đặc điểm của chủ nghĩa đế quốc Nhật cuối thế kỷ XIX đầu thế kỷ XX chủ nghĩa đế quốc phong kiến quân phiệt. Chọn D.
Câu 103:
 Xem đáp án
Xem đáp án
Duy trì hòa bình và an ninh thế giới là mục đích hoạt động chứ không phải nguyên tắc hoạt động của Liên hợp quốc. Chọn C.
Câu 104:
 Xem đáp án
Xem đáp án
Dựa vào sức mạnh quân sự, kinh tế để triển khai chiến lược toàn cầu với tham vọng làm bá chủ thế giới. Tháng 3-1947, trong diễn văn đọc trước Quốc hội Mĩ, Tổng thống Truman công khai tuyên bố: "Sứ mệnh lãnh đạo thế giới tự do chống lại sự bành trướng của chủ nghĩa cộng sản".
- Mục tiêu của "Chiến lược toàn cầu":
+ Ngăn chặn, đẩy lùi và tiến tới tiêu diệt hoàn toàn CNXH.
+ Đàn áp phong trào GPDT, phong trào cộng sản và công nhân quốc tế, phong trào chống chiến tranh, vì hòa bình, dân chủ trên thế giới.
+ Khống chế, chi phối các nước đồng minh.
Chọn D.
Câu 105:
 Xem đáp án
Xem đáp án
Năm 1960 lịch sử ghi nhận là “Năm châu Phi" vì có 17 nước châu Phi giành độc lập. Chọn D.
Câu 106:
 Xem đáp án
Xem đáp án
Một yếu tố quan trọng tác động đến mức độ giành độc lập của các nước trong khu vực Đông Nam Á vào năm 1945 là nhận thức về vấn đề thời cơ của các nước khác nhau. Các nước chớp được thời cơ, có sự chuẩn bị lâu dài như Việt Nam sẽ có được mức độ độc lập cao, đã giành được chính quyền, còn ở Inđônêxia thi mới tuyên bố độc lập mà chưa giành được chính quyền. Chọn B.
Câu 107:
 Xem đáp án
Xem đáp án
Sự phát triển vượt bậc của kinh tế Mĩ và sự hồi phục nhanh chóng của kinh tế Nhật Bản, Tây Âu sau Chiến tranh thế giới thứ hai là do biết tận dụng những cơ hội thuận lợi từ bên ngoài. Nếu Mĩ lợi dụng chiến tranh để làm giàu từ bán vũ khí, trong khi đó Nhật Bản và Tây Âu đều tập dụng tốt vào nguồn viện trợ của Mĩ. Chọn A.
Câu 108:
 Xem đáp án
Xem đáp án
Thời cơ của cách mạng tháng Tám bao gồm nguyên nhân chủ quan và nguyên nhân khách quan. Trong đó, nội dung của các phương án A, C, D là nguyên nhân chủ quan quyết định sự thắng lợi của cách mạng tháng Tám. Còn nội dung của phương án B là nguyên nhân khách quan giúp cho cuộc cách mạng tháng Tám diễn ra nhanh chóng và ít đổ máu vì kẻ thù của ta đã suy yếu nghiêm trọng. Chọn B.
Câu 109:
 Xem đáp án
Xem đáp án
Theo yêu cầu của Mặt trận đoàn kết dân tộc cứu nước Campuchia, quân đội Việt Nam cùng với lực lượng cách mạng Campuchia tiến công, xoá bỏ chế độ diệt chủng PônPốt. Ngày 7-1-1979, Thủ đô PhnômPênh được giải phóng. Chọn B.
Câu 110:
 Xem đáp án
Xem đáp án
A loại vì cuộc kháng chiến chống Mĩ, cứu nước đã kết thúc năm 1975.
B loại vì cuộc kháng chiến chống Pháp kết thúc năm 1954.
C loại vì ta đã giành chính quyền từ năm 1945.
Chọn D vì trong những năm 1976-1986, chúng ta phải đấu tranh bảo vệ độc lập với chiến tranh bảo vệ biên giới phía Bắc và chiến tranh bảo vệ biên giới Tây Nam.
Câu 111:
 Xem đáp án
Xem đáp án
Chính sách dân số 1 con đã kiềm chế tốc độ gia tăng dân số của Trung Quốc song để lại nhiều hậu quả không mong muốn, trong đó có tình trạng mất cân bằng giới tính nghiêm trọng do tâm lí và tư tưởng của người dân Trung Quốc muốn sinh bé trai hơn bé gái. (Kiến thức lớp 11 bài 10). Chọn B.
Câu 112:
 Xem đáp án
Xem đáp án
Mục tiêu tổng quát của ASEAN là đoàn kết và hợp tác vì một ASEAN hòa bình, ổn định cùng phát triển (SGK Địa 11, bài 11, tiết 3). Chọn B.
Câu 113:
 Xem đáp án
Xem đáp án
Sự phong phú về thành phần loài được quyết định bởi nước ta nằm trên đường di cư và di lưu của nhiều loài thực vật. Chọn D.
Câu 114:
 Xem đáp án
Xem đáp án
Vùng đồi núi nằm ở phía tây, cách xa biển nên không thể xảy ra triều cường và xâm nhập mặn. Chọn B.
Câu 115:
 Xem đáp án
Xem đáp án
Căn cứ vào Atlat địa lí Việt Nam trang 15, tỉ trọng dân số nông thôn ngày càng giảm (từ 84,3% năm 1960 xuống 72,6% năm 2007) → do vậy nhận xét C tỉ trọng dân nông thôn ngày càng tăng là sai. Chọn C.
Câu 116:
Cho bảng số liệu sau:
ĐẦU TƯ TRỰC TIẾP CỦA NƯỚC NGOÀI ĐƯỢC CẤP GIẤY PHÉP
PHÂN THEO VÙNG NƯỚC TA NĂM 2021
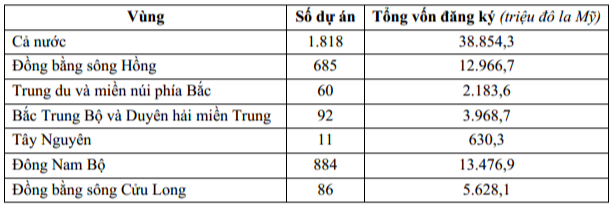
(Nguồn: gso.gov.vn)
Để thể hiện số dự án và tổng vốn đăng ký được cấp giấy phép phân chia theo vùng của nước ta năm 2021, dạng biểu đồ nào sau đây là phù hợp?
 Xem đáp án
Xem đáp án
Để thể hiện số dự án và tổng vốn đăng ký → 2 loại đơn vị nhưng chỉ có 1 năm, biểu đồ cột là phù hợp nhất (không vẽ được kết hợp vì kết hợp cần nhiều năm). Chọn A.
Câu 117:
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
A. Cơ sở vật chất hiện đại hóa nhanh chóng. → đúng
B. Ngành non trẻ nhưng phát triển rất nhanh. »→ đúng.
C. Mở nhiều đường bay thẳng đến các nước. → đúng.
D. Vận chuyển khối lượng hàng hóa lớn nhất. → Sai, đường hàng không không có khối lượng vận chuyển lớn nhất, đường hàng không chủ yếu vận chuyển người. Chọn D.
Câu 118:
 Xem đáp án
Xem đáp án
Ngành công nghiệp năng lượng của nước ta cần phát triển đi trước một bước. Từ đó các ngành khác mới có thể phát triển. Chọn D.
Câu 119:
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
A. Thường xuyên bị khô hạn. → Sai, đất ở đây không thường xuyên khô hạn.
B. Sử dụng chưa hợp lí, hệ số sử dụng cao. → đúng. Chọn B.
C. Bón quá nhiều phân hữu cơ. → không phải nguyên nhân chủ yếu.
D. Xói mòn, rửa trôi diễn ra mạnh. → xói mòn chủ yếu ở miền núi.
Đất ở ĐBSH đang bị xuống cấp do sử dụng chưa hợp lý, hệ số sử dụng cao.
Câu 120:
 Xem đáp án
Xem đáp án
Giá trị nông sản nói chung, thuỷ sản nói riêng được nâng cao khi làm chủ được khâu chế biến. Mặt khác, việc xuất khẩu thuỷ sản thu lại lợi nhuận lớn. Chọn A.
Câu 121:
 Xem đáp án
Xem đáp án
\(\vec F = q\vec E\), nếu \({\rm{q}} > 0\) thì cường độ điện trường \({\rm{E}}\) cùng chiều với lực điện \({\rm{F}}\), nếu \({\rm{q}} < 0\) thì cường độ điện trường E ngược chiều với lực điện F. Chọn D.
Câu 122:
 Xem đáp án
Xem đáp án
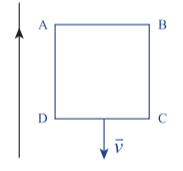
Ta có khung dây chuyển động song song với dòng điện thẳng dài \( \to \) Cảm ứng từ qua khung dây không thay đổi \( \to \) Từ thông qua khung dây không biến thiên hay nói cách khác không có dòng điện cảm ứng trong khung. Chọn B.
Câu 123:
 Xem đáp án
Xem đáp án
Ta có góc i = i' mà i’ + r = 90o \( \to i + r = 90^\circ \to \cos i = \sin r\)
Công thức khúc xạ: \(\sin i = n \cdot \sin r \to \sin i = n \cdot \cos i \to \tan i = n = \frac{4}{3} \to i = 53^\circ \)
Chọn C.
Câu 124:
Tháng 4/1983, một lữ đoàn lính diễu hành bước đều qua cầu treo Broughton của Anh. Theo các ghi chép vào thời điểm đó, cây cầu đã bị đổ gãy dưới chân các binh sĩ, hàng chục người rơi xuống nước. Sau khi điều này xảy ra, quân đội Anh đã ban hành quy định mới: binh lính khi đi qua một cây cầu dài không được đi bước đều hoặc diễu hành nhịp nhàng, để đề phòng sự cố tái diễn. Sự kiện trên đề cập đến vấn đề trong vật lí nào dưới đây?

 Xem đáp án
Xem đáp án
Sự kiện trên đề cập đến vấn đề cộng hưởng cơ. Chọn C.
Câu 125:
 Xem đáp án
Xem đáp án
Câu 126:
 Xem đáp án
Xem đáp án
Trong sơ đồ khối của máy phát thanh vô tuyến đơn giản không có bộ phận mạch tách sóng.
Chọn A.
Câu 127:
Ngày nay, trong các phòng thí nghiệm vật lý, người ta hay dùng tia laze để thực nghiệm giao thoa khe Y-âng bởi vì tính chất nổi bật nào dưới đây của tia laze?
 Xem đáp án
Xem đáp án
Ngày nay, trong các phòng thí nghiệm vật lý, người ta hay dùng tia laze để thực nghiệm giao thoa khe Y-âng bởi vì tính đơn sắc cao. Chọn C.
Câu 128:
 Xem đáp án
Xem đáp án
Ta có \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = 50\;{\rm{V}}\). Chọn C.
Câu 129:
 Xem đáp án
Xem đáp án
Gọi n1 và n2 lần lượt là số vân sáng quan sát được trên màn của hai bức xạ
Ta có: \[\left\{ \begin{array}{l}{n_1} + {n_2} = 13\\{n_2} - {n_1} = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{n_1} = 5\\{n_2} = 8\end{array} \right.\]
Vậy vị trí trùng nhau gần nhất với vân trung tâm ứng với vân sáng bậc 6 của bức xạ λ1 và vân sáng bậc 9 của bức xạ λ2.
Ta có: \[\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} \Rightarrow \frac{6}{9} = \frac{{{\lambda _2}}}{{0,6}} \Rightarrow {\lambda _2} = 0,4\,\mu m\]
Chọn A.
Câu 130:
Một sợi dây đàn hồi dài 1 m, có hai đầu cố định được căng ngang. Kích thích cho đầu A của dây dao động với tần số 680 Hz thì trên dây có sóng dừng ổn định với A và B là hai nút sóng. Tốc độ truyền sóng trên dây là \(340\;{\rm{m}}/{\rm{s}}.\) Trên dây, số điểm dao động với biên độ bằng một nửa biên độ dao động của một bụng sóng là
Đáp án: ……….
 Xem đáp án
Xem đáp án
Bước sóng: \(\lambda = \frac{v}{f} = \frac{{340}}{{680}} = 0,5\;{\rm{m}}\)
Điều kiện có sóng dừng trên dây hai đầu cố định: \(\ell = k\frac{\lambda }{2} \Rightarrow k = \frac{{2\ell }}{\lambda } = \frac{{2.1}}{{0,5}} = 4\)
Vậy sóng dừng trên dây với 4 bó sóng.
Mỗi bó sóng có 2 điểm dao động với biên độ bằng một nửa biên độ dao động của một bụng sóng.
\( \Rightarrow 4\) bó sóng có 8 điểm dao động với biên độ bằng một nửa biên độ dao động của một bụng sóng.
Đáp án: 8
Câu 131:
 Xem đáp án
Xem đáp án
Malic acid có công thức cấu tạo: \({\rm{HOOC}} - {\rm{CH}}({\rm{OH}}) - {\rm{C}}{{\rm{H}}_2} - {\rm{COOH}}\)
\(\begin{array}{l}{\rm{HOOC}} - {\rm{CH}}({\rm{OH}}) - {\rm{C}}{{\rm{H}}_2} - {\rm{COOH}} + 3{\rm{Na}} \to {\rm{NaOOC}} - {\rm{CH}}({\rm{ONa}}) - {\rm{C}}{{\rm{H}}_2} - {\rm{COONa}} + 1,5{{\rm{H}}_2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1,5a\,\,mol\end{array}\)
\(\begin{array}{l}{\rm{HOOC}} - \mathop {\rm{C}}\limits_{|\,} {\rm{H}} - {\rm{C}}{{\rm{H}}_2} - {\rm{COOH}} + 2{\rm{NaHC}}{{\rm{O}}_3} \to {\rm{NaOOC}} - \mathop {\rm{C}}\limits_| {\rm{H}} - {\rm{C}}{{\rm{H}}_2} - {\rm{COONa}} + 2{\rm{C}}{{\rm{O}}_2} + 2{{\rm{H}}_2}{\rm{O}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,OH\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,OH\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{a}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{2a}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{mol}}\end{array}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{\rm{n}}_{{{\rm{H}}_2}}} = 1,5{\rm{a}}}\\{{{\rm{n}}_{{\rm{C}}{{\rm{O}}_2}}} = 2{\rm{a}}}\end{array} \Rightarrow \frac{{{{\rm{V}}_1}}}{{\;{{\rm{V}}_2}}} = \frac{{1,5}}{2} \Rightarrow 4\;{{\rm{V}}_1} = 3\;{{\rm{V}}_2}} \right.\).
Chọn B.
Câu 132:
Cho hai bình như nhau, bình A chứa 0,5 lít hydrochloric acid 2M; bình B chứa 0,5 lít acetic acid 2M được bịt kín bởi hai bóng cao su như nhau. Hai mẫu Mg khối lượng như nhau được thả xuống cùng một lúc. Kết quả sau 1 phút và sau 10 phút (phản ứng đã kết thúc) được thể hiện ở bình dưới đây?
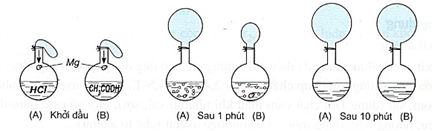
Nhận định nào sau đây không đúng?
 Xem đáp án
Xem đáp án
Nhận định không đúng là: "Acetic acid có phân tử khối lớn hơn nên tại thời điểm 1 phút, tốc độ thoát khí chậm hơn" vì tốc độ phản ứng hoá học phụ thuộc vào nhiệt độ, nồng độ, áp suất, chất xúc tác, diện tích bề mặt; tốc độ phản ứng không ảnh hưởng bởi phân tử khối.
Chọn C.
Câu 133:
 Xem đáp án
Xem đáp án
Các phương trình hóa học:
Hòa tan X trong HCl dư:
\(2{\rm{Al}} + 6{\rm{HCl}} \to 2{\rm{AlC}}{{\rm{l}}_3} + 3{{\rm{H}}_2}\)
\({\rm{Fe}} + 2{\rm{HCl}} \to {\rm{FeC}}{{\rm{l}}_2} + {{\rm{H}}_2}\)
\({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3} + 6{\rm{HCl}} \to 2{\rm{AlC}}{{\rm{l}}_3} + 3{{\rm{H}}_2}{\rm{O}}\)
\({\rm{F}}{{\rm{e}}_3}{{\rm{O}}_4} + 8{\rm{HCl}} \to {\rm{FeC}}{{\rm{l}}_2} + 2{\rm{FeC}}{{\rm{l}}_3} + 4{{\rm{H}}_2}{\rm{O}}\)
Bảo toàn O: \[{{\rm{n}}_{{H_2}O}} = {{\rm{n}}_{{\rm{O}}\,\,{\rm{(ox}}ide{\rm{) }}}} = 0,04 \cdot 4 = 0,16\]mol
Bảo toàn H: \({{\rm{n}}_{{\rm{HCl}}}} = 2{{\rm{n}}_{{{\rm{H}}_2}}} + 2{{\rm{n}}_{{{\rm{H}}_2}{\rm{O}}}} = 2 \cdot 0,15 + 2 \cdot 0,16 = 0,62\;\)mol
Bảo toàn khối lượng ta có:
\({{\rm{m}}_{\rm{x}}} + {{\rm{m}}_{{\rm{HCl}}}} = {\rm{m}} + {{\rm{m}}_{{{\rm{H}}_2}}} + {{\rm{m}}_{{{\rm{H}}_2}{\rm{O}}}}\)
\( \Rightarrow {\rm{m}} = 0,12 \cdot 27 + 0,04 \cdot 232 + 0,62 \cdot 36,5 - 0,15 \cdot 2 - 0,16 \cdot 18 = 31,97{\rm{ }}\)gam.
Chọn D.
Câu 134:
 Xem đáp án
Xem đáp án
\({{\rm{n}}_{\rm{x}}} = \frac{{13,35}}{{89}} = 0,15\;{\rm{mol}}\).
Ta có: \({{\rm{n}}_{\rm{x}}} + {{\rm{n}}_{{\rm{NaOH}}}} = {{\rm{n}}_{{\rm{HCl}}}} \Rightarrow {{\rm{n}}_{{\rm{NaOH}}}} = 0,25 \cdot 1 - 0,15 = 0,1\;{\rm{mol}} \Rightarrow {\rm{V}} = 0,1\)lít = 100 mL.
Chọn A.
Câu 135:
Công thức Lewis của ion oxalate được cho như hình bên dưới. Mỗi nguyên tử carbon dùng bao nhiêu electron để tham gia tạo liên kết?
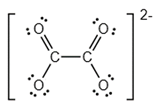
 Xem đáp án
Xem đáp án
Dựa vào công thức Lewis của ion oxalate thấy rằng mỗi nguyên tử carbon đã sử dụng 4 electron để tham gia tạo liên kết.
Chọn C.
Câu 136:
Nitrogen dioxide \(\left( {{\rm{N}}{{\rm{O}}_2}} \right)\) là nguyên liệu điều chế nhiều chất vô cơ. Sơ đồ hình dưới đây biểu diễn quá trình điều chế một số chất vô cơ từ nitrogen dioxide:
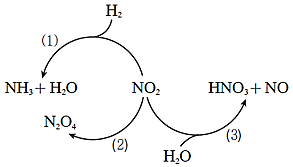
Quá trình điều chế một số chất vô cơ từ nitrogen dioxide
Cho các phát biểu sau:
(a) Trong phản ứng (1), \({{\rm{H}}_2}\) là chất khử.
(b) Trong phản ứng (2), \({\rm{N}}{{\rm{O}}_2}\) bị oxi hóa.
(c) Trong quá trình trên, hợp chất chứa nguyên tử \({\rm{N}}\) có số oxi hóa cao nhất là \({\rm{HN}}{{\rm{O}}_3}.\)
(d) Trong phản ứng (3), \({{\rm{H}}_2}{\rm{O}}\) là chất oxi hóa.
Số phát biểu đúng với sơ đồ trên là
 Xem đáp án
Xem đáp án
Phát biểu đúng: (a), (c)
Phát biểu (b) sai vì: Trong phản ứng (2), N không thay đổi số oxi hóa.
Phát biểu (d) sai vì: \(3\mathop {\;{\rm{N}}}\limits^{ + 4} {{\rm{O}}_2} + {{\rm{H}}_2}{\rm{O}} \to 2H\mathop N\limits^{ + 5} {{\rm{O}}_3} + \mathop {\;{\rm{N}}}\limits^{ + 2} {\rm{O}}\)
\({\rm{N}}{{\rm{O}}_2}\) vừa đóng vai trò là chất oxi hóa, vừa đóng vai trò là chất khử.
Chọn B.
Câu 137:
\({\rm{MgC}}{{\rm{l}}_2}\) nóng chảy có thể bị phân hủy thành các nguyên tố nếu như đặt một điện áp đủ lớn vào hai điện cực trơ. Sản phẩm của phản ứng là \({\rm{Mg}}\) nóng chảy (ở cực âm) và khí \({\rm{C}}{{\rm{l}}_2}\) (ở cực dương). Dưới đây là một sơ đồ đơn giản của quá trình điện phân nóng chảy \({\rm{MgC}}{{\rm{l}}_2}.\)
Nếu dòng điện trong bình được giữ ở mức không đổi \(5\;{\rm{A}}\), giả sử hằng số Faraday bằng \(96485{\rm{C}}\) thì mất bao nhiêu giây để tạo ra 2,00 gam Mg (l) ở cực âm?
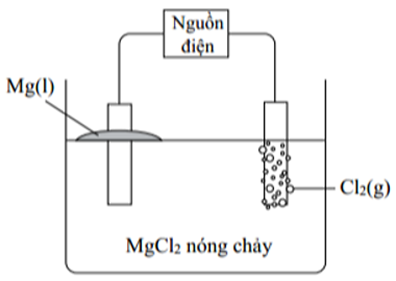
 Xem đáp án
Xem đáp án
\({n_{Mg}} = \frac{2}{{24}} = \frac{1}{{12}}\,(\;{\rm{mol}})\)
Ta có phương trình điện phân nóng chảy:
Quá trình oxi hóa:
\(\begin{array}{*{20}{c}}{Mg \to M{g^{2 + }} + 2e}&{}\\{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{{12}} \to \,\,\,\frac{1}{6}\,}&{mol}\end{array}\)
\({n_e} = \frac{{It}}{F} \Rightarrow \frac{1}{6} = \frac{{5t}}{{96485}} \Rightarrow t = 3216\;{\rm{s}}\)
Chọn C.
Câu 138:
 Xem đáp án
Xem đáp án
Chất điện li là chất khi tan trong nước (hoặc ở trạng thái nóng chảy) có khả năng phân li thành các ion Þ chất phải ở trạng thái nóng chảy hoặc trong nước.
Chọn A.
Câu 139:
Muối tiêu Chile là một loại muối có chứa \({\rm{NaN}}{{\rm{O}}_3}\)và một lượng nhỏ \({\rm{NaI}}{{\rm{O}}_3}{\rm{.}}\)\({\rm{NaI}}{{\rm{O}}_3}\) có thể được sử dụng làm nguồn cung cấp iodine cực kì tốt cho cơ thể và nó được tạo ra trong các phản ứng như sau:
\({\rm{IO}}_3^ - + 3{\rm{HSO}}_3^ - \to {{\rm{I}}^ - } + 3{{\rm{H}}^ + } + 3{\rm{SO}}_4^{2 - }\,\,\,\,\,\,\,\,\,\,(1)\)
\(5{{\rm{I}}^ - } + {\rm{IO}}_3^ - + 6{{\rm{H}}^ + } \to 3{{\rm{I}}_2} + 3{{\rm{H}}_2}{\rm{O }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{(2) }}\)
Một lít dung dịch muối tiêu Chile có chứa 5,94 gam \({\rm{NaI}}{{\rm{O}}_3}\) được xử lý bằng dung dịch \({\rm{NaHS}}{{\rm{O}}_3}\) dư theo phản ứng (1). Tiếp theo, một lượng dung dịch cùng khối lượng \({\rm{NaI}}{{\rm{O}}_3}\) với ban đầu được thêm tiếp vào hỗn hợp phản ứng để tiếp tục thực hiện phản ứng (2). Biết nguyên tử khối của I là 127. Mỗi lít muối Chile có thể tạo ra bao nhiêu gam \({{\rm{I}}_2}\)?
 Xem đáp án
Xem đáp án
\({n_{{\rm{NaI}}{{\rm{O}}_3}}} = \frac{{5,94}}{{23 + 127 + 16 \cdot 3}} = 0,03\;{\rm{mol}}\)
\(\begin{array}{l}{\rm{IO}}_3^ - + 3{\rm{HSO}}_3^ - \to {{\rm{I}}^ - } + 3{{\rm{H}}^ + } + 3{\rm{SO}}_4^{2 - }\\0,03\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0,03\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,mol\end{array}\)
\(\begin{array}{l}5{{\rm{I}}^ - } + {\rm{IO}}_3^ - + 6{{\rm{H}}^ + } \to 3{{\rm{I}}_2} + 3{{\rm{H}}_2}{{\rm{O}}_{}}\\0,03\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0,018\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{mol}}\end{array}\)
Vậy \({m_{{{\rm{I}}_2}}} = 0,018 \cdot 127 \cdot 2 = 4,572\) gam.
Chọn A.
Câu 140:
Hỗn hợp T gồm ba ester X, Y, Z mạch hở \(\left( {{M_X} < {M_Y} < {M_Z}} \right).\) Cho 48,28 gam T tác dụng vừa đủ với dung dịch chứa \(0,47\;{\rm{mol}}\,\,{\rm{NaOH,}}\) thu được một muối duy nhất của carboxylic acid đơn chức và hỗn hợp Q gồm các alcohol no, mạch hở, có cùng số nguyên tử carbon trong phân tử. Đốt cháy hoàn toàn Q thu được 14,874 lít khí \({\rm{C}}{{\rm{O}}_2}\) (đkc) và 14,4 gam \({{\rm{H}}_2}{\rm{O}}.\) Số nguyên tử \({\rm{H}}\) có trong công thức phân tử của Y là
Đáp án: ……….
 Xem đáp án
Xem đáp án
* Khi đốt cháy hỗn hợp Q (các alcohol no, mạch hở):
\({n_{C{O_2}}} = 0,6\,mol;\,{n_{{H_2}O}} = 0,8\,mol\)
\( \Rightarrow {{\rm{n}}_{\rm{Q}}} = {{\rm{n}}_{{{\rm{H}}_2}{\rm{O}}}} - {{\rm{n}}_{{\rm{C}}{{\rm{O}}_2}}} = 0,2\;{\rm{mol}}\)
Þ Số C của alcohol = \(\frac{{0,6}}{{0,2}} = 3\)
Kết hợp với sau khi thủy phân trong môi trường base thu được một muối + các alcohol; \({M_X} < {M_Y} < {M_Z}\)
Þ Q gồm 3 alcohol là \({{\rm{C}}_3}{{\rm{H}}_8}{\rm{O}};{{\rm{C}}_3}{{\rm{H}}_8}{{\rm{O}}_2}\) và \({{\rm{C}}_3}{{\rm{H}}_8}{{\rm{O}}_3}.\)
\({n_{ - COO - }} = {n_{ - OH\,(alcohol)}} = {n_{NaOH}} = 0,47\,mol\)
Theo đó, \({m_Q} = {m_C} + {m_H} + {m_O} \Rightarrow {m_Q} = 0,6 \cdot 12 + 0,8 \cdot 2 + 0,47 \cdot 16 = 16,32\) gam.
* Thủy phân:
48,28 gam T + 0,47 mol NaOH \( \to 0,47\) mol RCOONa + 16,32 gam hỗn hợp alcohol Q.
Bảo toàn khối lượng, ta có \({m_{RCOONa}} = 50,76\) gam
\(\begin{array}{l} \Rightarrow R + 44 + 23 = \frac{{50,76}}{{0,47}}\\ \Rightarrow R = 41\,\,\,({C_3}{H_5} - )\end{array}\)
Vậy ester \({\rm{Y}}\) tương ứng là \({\left( {{{\rm{C}}_3}{{\rm{H}}_5}{\rm{COO}}} \right)_2}{{\rm{C}}_3}{{\rm{H}}_6},\) có công thức phân tử: \({{\rm{C}}_{11}}{{\rm{H}}_{16}}{{\rm{O}}_4}.\)
Số nguyên tử \({\rm{H}}\) có trong công thức phân tử của Y là 16.
Đáp án: 16
Câu 141:
 Xem đáp án
Xem đáp án
Ở động vật, quá trình tiêu hóa hóa học diễn ra chủ yếu ở ruột non, ở đây có các enzim tiêu hóa để tiêu hóa thức ăn thành các chất dinh dưỡng. Chọn B.
Câu 142:
Người ta phân biệt nhóm thực vật C3, C4 chủ yếu dựa vào
 Xem đáp án
Xem đáp án
Người ta phân biệt nhóm thực vật C3, C4 chủ yếu dựa vào sản phẩm cố định CO2 đầu tiên: Sản phẩm cố định CO2 đầu tiên của thực vật C3 là APG (hợp chất 3C), sản phẩm cố định CO2 đầu tiên của thực vật C4 là một hợp chất 4C. Chọn D.
Câu 143:
 Xem đáp án
Xem đáp án
Sự biến động nồng độ của hoocmôn sinh dục gồm prôgestêrôn và ơstrôgen theo chu kì chính là nguyên nhân dẫn tới trứng được rụng theo chu kì ở người phụ nữ. Chọn B.
Câu 144:
 Xem đáp án
Xem đáp án
Vùng vận hành là nơi gắn với prôtêin ức chế ngăn cản quá trình phiên mã diễn ra khi môi trường không có lactôzơ. Do đó, nếu đột biến xảy ra ở vùng vận hành khiến cho prôtêin ức chế không thể gắn vào vùng vận hành sẽ có thể làm cho các gen cấu trúc Z, Y, A phiên mã ngay cả khi môi trường không có lactôzơ. Chọn A.
Câu 145:
 Xem đáp án
Xem đáp án
Tính trạng màu hoa do gen ngoài nhân quy định, nên F1 mang kiểu hình giống mẹ. Mà trong phép lai này, mẹ (cơ thể cái) có kiểu hình hoa đỏ nên đời con 100% hoa đỏ. Chọn B.
Câu 146:
 Xem đáp án
Xem đáp án
Tần số kiểu gen aa trong quần thể \[ = \frac{{40}}{{960 + 40}} = 0,04\].
Vì quần thể đang ở trạng thái cân bằng di truyền nên tần số alen \(a = \sqrt {aa} = \sqrt {0,04} = 0,2.\)
\( \to A = 1 - 0,2 = 0,8\).
Vậy A = 0,8; a = 0,2. Chọn C.
Câu 147:
 Xem đáp án
Xem đáp án
Trong hệ sinh thái, quá trình sử dụng năng lượng Mặt trời để tổng hợp các chất hữu cơ được thực hiện bởi nhóm sinh vật sản xuất, trong đó chủ yếu là thực vật. Chọn A.
Câu 148:
 Xem đáp án
Xem đáp án
Hiện tượng kháng thuốc ở vi khuẩn tụ cầu vàng trong trường hợp này là một ví dụ cho quá trình hình thành quần thể thích nghi. Quá trình này xảy ra nhanh hay chậm phụ thuộc vào 3 yếu tố: quá trình phát sinh và tích lũy các gen đột biến ở mỗi loài, tốc độ sinh sản của loài, áp lực chọn lọc tự nhiên (việc sử dụng các loại thuốc). Vậy A, B, C đúng. Chọn D.
Câu 149:
Một tế bào sinh tinh có kiểu gen \(\frac{{AB}}{{ab}}Dd\) đang giảm phân, trong đó cặp NST chứa hai cặp gen A, a và B, b không phân li ở giảm phân I, giảm phân II diễn ra bình thường; cặp D, d và các cặp NST khác phân li bình thường. Biết các gen không xảy ra hoán vị. Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
I. Kết thúc quá trình giảm phân tạo ra 4 giao tử đột biến.
II. Giao tử được tạo ra có thể có kiểu gen AB hoặc abDd.
III. Các giao tử được tạo ra có bộ NST là (n + 1) và (n - 1).
IV. Số loại giao tử tối đa được tạo ra là 2.
 Xem đáp án
Xem đáp án
Tế bào có kiểu gen \(\frac{{AB}}{{ab}}Dd\) giảm phân không xảy ra hoán vị có:
+ Cặp \(\frac{{AB}}{{ab}}\) không phân li trong giảm phân I cho 2 loại giao tử: \(2\frac{{AB}}{{ab}}:2O.\)
+ Cặp Dd giảm phân bình thường cho 2 loại giao tử: 2D : 2d.
Vậy tế bào này cho 2 loại giao tử với 2 trường hợp: \(2\frac{{AB}}{{ab}}D:2d\) hoặc \(2\frac{{AB}}{{ab}}d:2D.\)
Xét sự đúng – sai của các phát biểu:
I. Đúng. Kết thúc quá trình giảm phân cho 4 giao tử đột biến với 2 loại: \(2\frac{{AB}}{{ab}}D:2d\) hoặc \(2\frac{{AB}}{{ab}}d:2D\).
II. Sai. Hai cặp gen A, a và B, b không phân li ở giảm phân I, giảm phân II diễn ra bình thường; cặp D, d và các cặp NST khác phân li bình thường nên giao tử được tạo ra không thể có kiểu gen AB hoặc abDd.
III. Đúng. Ví dụ \(\frac{{AB}}{{ab}}D\) là giao tử (n + 1), giao tử d là giao tử (n – 1).
IV. Đúng. Tế bào này không xảy ra hoán vị gen sẽ cho tối đa 2 loại giao tử với 2 trường hợp: \(2\frac{{AB}}{{ab}}D:2d\) hoặc \(2\frac{{AB}}{{ab}}d:2D\).
Chọn D.
