Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 17)
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 17)
-
383 lượt thi
-
150 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Hình vẽ dưới đây là báo cáo phân tích tài chính, tổng sản phẩm nội địa, tức tổng sản phẩm quốc nội hay GDP (viết tắt của Gross Domestic Product) của Việt Nam trong giai đoạn từ 2010-2021. Tuy dịch bệnh khó khăn nhưng theo ADB, kinh tế nước ta sẽ sớm phục hồi trong tương lai nhờ các nền tảng tốt.
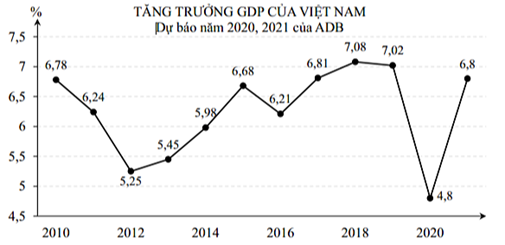
Trong những giai đoạn sau, giai đoạn nào GDP Việt Nam có sự tăng trưởng liên tục?
 Xem đáp án
Xem đáp án
Câu 2:
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho hình thang \[ABCD\] vuông tại \[A\] và \[B.\] Ba đỉnh \[A\left( {1\,;\,\,2\,;\,\,1} \right),\,\,B\left( {2\,;\,\,0\,;\,\, - 1} \right),\,\,C\left( {6\,;\,\,1\,;\,\,0} \right).\] Hình thang có diện tích bằng \(6\sqrt 2 .\) Giả sử \(D\left( {a\,;\,\,b\,;\,\,c} \right)\), tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Ta có \(\overrightarrow {AB} = \left( {1\,;\,\, - 2\,;\,\, - 2} \right) \Rightarrow \left| {\overrightarrow {AB} } \right| = 3\,;\,\,\overrightarrow {BC} = \left( {4\,;\,\,1\,;\,\,1} \right) \Rightarrow \left| {\overrightarrow {BC} } \right| = 3\sqrt 2 .\)
Theo giả thiết ABCD là hình thang vuông tại \(A\) và \(B\) và có diện tích bằng \(6\sqrt 2 \) nên
\(\frac{1}{2}AB\left( {AD + BC} \right) = 6\sqrt 2 \Leftrightarrow \frac{1}{2} \cdot 3 \cdot \left( {AD + 3\sqrt 2 } \right) = 6\sqrt 2 \Rightarrow AD = \sqrt 2 \Rightarrow AD = \frac{1}{3}BC.\)
Do \[ABCD\] là hình thang vuông tại \(A\) và \(B\) nên \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {BC} .\)
Giả sử \[D\left( {a\,;\,\,b\,;\,\,c} \right)\] khi đó ta có \(\left\{ {\begin{array}{*{20}{l}}{a - 1 = \frac{4}{3}}\\{b - 2 = \frac{1}{3}}\\{c - 1 = \frac{1}{3}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{7}{3}}\\{b = \frac{7}{3}}\\{c = \frac{4}{3}}\end{array} \Rightarrow a + b + c = 6} \right.} \right..\)
Chọn A.
Câu 3:
Một ô tô đang chạy với vận tốc \(15\,\,\;{\rm{m}}/{\rm{s}}\) thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển động chậm dần đều với vận tốc \(v(t) = - 5t + 15\,\,(\;{\rm{m}}/{\rm{s}})\) trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét?
 Xem đáp án
Xem đáp án
Khi ô tô dừng hẳn thì \(V\left( t \right) = 0 \Leftrightarrow - 5t + 15 = 0 \Leftrightarrow t = 3\).
Quãng đường di chuyển của ô tô từ lúc hãm phanh đến khi dừng hẳn là
\(S = \int\limits_0^3 {\left( { - 5t + 15} \right)dt} = \left. {\left( { - \frac{{5{t^2}}}{2} + 15t} \right)} \right|_0^3 = 22,5\;\,({\rm{m)}}{\rm{. }}\)Chọn A.
Câu 4:
 Xem đáp án
Xem đáp án
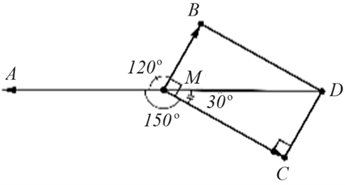
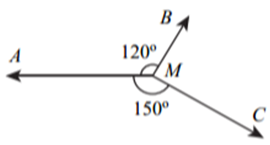
Ta có \(\widehat {AMB} = 120^\circ ,\,\,\widehat {AMC} = 150^\circ \)
\( \Rightarrow \widehat {BMC} = 360^\circ - 120^\circ - 150^\circ = 90^\circ \)
\(\widehat {CMD} = 180^\circ - \widehat {AMC} = 180^\circ - 150^\circ = 30^\circ \)
Vì vật đứng yên nên tổng hợp lực tác động vào vật bằng \(0\) nên \(MD = MA = 50\)\(\cos \widehat {CMD} = \frac{{MC}}{{MD}} \Rightarrow MC = MD \cdot \cos 30^\circ = 50 \cdot \frac{{\sqrt 3 }}{2} = 25\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = {F_3} = MC = 25\sqrt 3 .\) Chọn B.
Câu 5:
Cho số phức \(z\) thỏa mãn \(\left( {3 + 2i} \right)z + {\left( {2 - i} \right)^2} = 4 + i.\) Mô đun của số phức \({\rm{w}} = \left( {z + 1} \right)\bar z\) bằng
 Xem đáp án
Xem đáp án
Ta có: \(\left( {3 + 2i} \right)z + {\left( {2 - i} \right)^2} = 4 + i \Leftrightarrow \left( {3 + 2i} \right)z = 1 + 5i \Leftrightarrow z = 1 + i.\)
Do đó: \[w = \left( {z + 1} \right)\bar z = z \cdot \bar z + \bar z = \left( {1 + i} \right)\left( {1 - i} \right) + 1 - i = 2 + 1 - i = 3 - i.\]
Do đó \(\left| w \right| = \sqrt {{3^2} + 1} = \sqrt {10} .\) Chọn B.
Câu 6:
 Xem đáp án
Xem đáp án
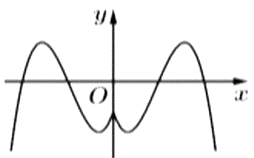
Từ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) suy ra đồ thị hàm số \(y = f\left( x \right)\) gồm:
- Nét cuối hướng xuống \( \Rightarrow a < 0\)
- Cắt trục tung tại điểm có tung độ âm \( \Rightarrow d < 0\)
- Hai điểm cực trị dương \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - \frac{{2b}}{{3a}} > 0}\\{{x_1}{x_2} = \frac{c}{{3a}} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b > 0}\\{c < 0}\end{array}} \right.} \right..\)
Vậy \(a < 0\,,\,\,b > 0\,,\,\,c < 0\,,\,\,d < 0.\) Chọn A.
Câu 7:
Thể tích \(V\) cầu khối nội tiếp hình lập phương cạnh \(a\) là
 Xem đáp án
Xem đáp án
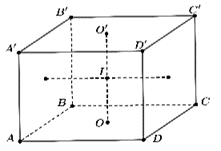
Dựa vào hình vẽ dễ nhận thấy bán kính mặt cầu nội tiếp hình lập phương là tâm \(I\), bán kính \(r = IO = \frac{a}{2}.\)
Thể tích của mặt cầu nội tiếp hình lập phương là:
\(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi \cdot {\left( {\frac{a}{2}} \right)^3} = \frac{{\pi {a^3}}}{6}{\rm{ (dvdt)}}{\rm{.}}\) Chọn A.Câu 8:
Phương trình \({x^3} - 6mx + 5 = 5{m^2}\) có 3 nghiệm phân biệt lập thành cấp số cộng khi
 Xem đáp án
Xem đáp án
Đặt \(y = f(x) = {x^3} - 6mx + 5 - 5{m^2}\) có \(f'(x) = 3{x^2} - 6m\,;\,\,f''(x) = 6x.\)
Phương trình đã cho có 3 nghiệm phân biệt
\( \Leftrightarrow \) Hàm số \(y = f(x)\) cắt trục hoành tại 3 điểm phân biệt
\( \Leftrightarrow f'(x) = 0\) có 2 nghiệm phân biệt \({x_1},{x_2}\) thoả mãn \(f\left( {{x_1}} \right).f\left( {{x_2}} \right) < 0.\)
Vì 3 nghiệm đó lập thành cấp số cộng nên \({x_2} - {x_1} = {x_3} - {x_2}.\)
Suy ra \({x_2}\) là hoành độ của tâm đối xứng hay là nghiệm của \(f''(x) = 0.\)
Cho \(f''(x) = 0 \Rightarrow 6x = 0 \Leftrightarrow x = 0.\)
Với \(x = 0\) ta có: \(5 - 5{m^2} = 0 \Leftrightarrow m = \pm 1.\)
Thử lại:
• Với \(m = 1\) thì ta có \({x^3} - 6x + 5 = 5 \Leftrightarrow x\left( {{x^2} - 6} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm \sqrt 6 }\end{array}} \right.\)
• Với \(m = - 1\) thì ta có \({x^3} + 6x + 5 = 5 \Leftrightarrow x\left( {{x^2} + 6} \right) = 0 \Leftrightarrow x = 0.\)
Chọn B.
Câu 9:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(f\left( 4 \right) = 2023,\,\,\int\limits_0^4 {f\left( x \right)dx} = 4.\) Tích phân \(\int\limits_0^2 {xf'\left( {2x} \right)dx} \) bằng
 Xem đáp án
Xem đáp án
Ta có \(\int\limits_0^2 {xf'\left( {2x} \right)dx} = \frac{1}{4}\int\limits_0^4 {tf'\left( t \right)dt} \)\( = \frac{1}{4}\int\limits_0^4 {xf'\left( x \right)dx} = \frac{1}{4}\left[ {\left. {xf\left( x \right)} \right|_0^4 - \int\limits_0^4 {f\left( x \right)dx} } \right]\)
\( = \frac{1}{4}\left[ {4 \cdot f\left( 4 \right) - \int\limits_0^4 {f\left( x \right)dx} } \right] = \frac{1}{4}\left( {4 \cdot 2023 - 4} \right) = 2022.\) Chọn A.
Câu 10:
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông cân tại \(A,\,\,AB = 2a,\,\,SA\) vuông góc với mặt đáy và góc giữa \[SB\] và mặt đáy bằng \(60^\circ .\) Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right).\) Giá trị \(\cos \alpha \) bằng
 Xem đáp án
Xem đáp án
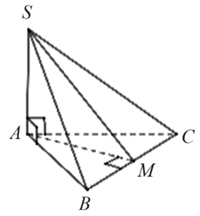
Gọi \(M\) là trung điểm \(BC \Rightarrow AM \bot BC\) (1)
Có \(\left\{ {\begin{array}{*{20}{l}}{BC \bot SA}\\{BC \bot AM}\end{array} \Rightarrow BC \bot SM} \right.\)
Từ (1) và \((2)\) suy ra \(\left( {\widehat {\left( {SBC} \right),\left( {ABC} \right)}} \right) = \widehat {SMA} = \alpha .\)
Do \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB\) và \[AB\] là hình chiếu vuông góc của \[SB\] lên \(\left( {ABC} \right) \Rightarrow \widehat {SBA} = 60^\circ .\)• Xét \(\Delta SAB\) có \(SA = AB \cdot \tan \widehat {SBA} = 2a \cdot \tan 60^\circ = 2\sqrt 3 a.\)
• Xét \(\Delta ABC\) có \(AM = \frac{1}{2}BC = \frac{1}{2}\sqrt {A{B^2} + A{C^2}} = \frac{1}{2}\sqrt {{{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} = a\sqrt 2 .\)
• Xét \(\Delta SAM\) vuông tại \(A\) có:
\(\cos \alpha = \frac{{AM}}{{SM}} = \frac{{AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \frac{{a\sqrt 2 }}{{\sqrt {{{\left( {2\sqrt 3 a} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} }} = \frac{1}{{\sqrt 7 }}.\) Chọn C.
Câu 11:
Số nghiệm nguyên của bất phương trình \(6\sqrt {\left( {x - 2} \right)\left( {x - 32} \right)} \ge {x^2} - 34x + 48\) là
 Xem đáp án
Xem đáp án
Ta có \(6\sqrt {\left( {x - 2} \right)\left( {x - 32} \right)} \ge {x^2} - 34x + 48 \Leftrightarrow 6\sqrt {{x^2} - 34x + 64} \ge {x^2} - 34x + 48\)
Đặt \(t = \sqrt {{x^2} - 34x + 64} \,\,\left( {t \ge 0} \right)\), suy ra \({x^2} - 34x + 48 = {t^2} - 16\).
Bất phương trình trở thành: \(6t \ge {t^2} - 16 \Leftrightarrow {t^2} - 6t - 16 \le 0 \Leftrightarrow - 2 \le t \le 8\)
Kết hợp điều kiện, suy ra \(0 \le t \le 8 \Leftrightarrow \sqrt {{x^2} - 34x + 64} \le 8 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - 34x + 64 \ge 0}\\{{x^2} - 34x + 64 \le 64}\end{array}} \right.\)
Vậy bất phương trình có 6 nghiệm nguyên \(x \in \left\{ {0\,;\,\,1\,;\,\,2\,;\,\,32\,;\,\,33\,;\,\,34} \right\}.\) Chọn B.
Câu 12:
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho tứ diện \[ABCD\] có \(A\left( {2\,;\,\, - 1\,;\,\,1} \right),\)\(B\left( {3\,;\,\,0\,;\,\, - 1} \right),\)\(C\left( {2\,;\,\, - 1\,;\,\,3} \right),\,\,D \in Oy\) và có thể tích bằng 5. Tổng tung độ của các điểm \(D\) là
 Xem đáp án
Xem đáp án
Do \(D \in Oy\) nên \(D\left( {0\,;\,\,y\,;\,\,0} \right)\).
Khi đó \[\overrightarrow {DA} = \left( {2\,;\, - 1 - y\,;\,1} \right),\,\,\overrightarrow {DB} = \left( {3\,;\, - y\,;\, - 1} \right),\,\,\overrightarrow {DC} = \left( {2\,;\, - 1 - y\,;\,3} \right).\]
Khi đó \(\left[ {\overrightarrow {DA} ,\,\,\overrightarrow {DB} } \right] = \left( {1 + 2y\,;\,\,5\,;\,y + 3} \right)\)
Và \[{V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {DA} ,\,\,\overrightarrow {DB} } \right] \cdot \overrightarrow {DC} } \right|{\rm{ }}{\mkern 1mu} = 5 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2y + 6 = 30}\\{2y + 6 = - 30}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 12}\\{y = - 18}\end{array}} \right.} \right..\]
Vậy \({y_1} + {y_2} = 12 - 18 = - 6.\) Chọn A.
Câu 13:
Một vật chuyển động với vận tốc thay đổi \(v(t) = 3k{t^2} + nt\,\,\left( {k,\,\,n \in \mathbb{R}} \right).\) Gọi \(S(t)\) là quãng đường đi được sau \(t\) giây. Biết rằng sau 5 giây thì quãng đường đi được là \[150{\rm{ }}m,\] sau 10 giây quãng đường đi được là \[1\,\,100{\rm{ }}m.\] Quãng đường vật đi được sau 30 giây bằng
 Xem đáp án
Xem đáp án
Ta có \(s\left( t \right) = \int v \left( t \right){\rm{d}}x = k{t^3} + \frac{1}{2}n{t^2}\)
Sau 5 giây, quãng đường đi được là \(s\left( 5 \right) = 150 \Leftrightarrow 125k + 12,5n = 150.\)
Sau 10 giây, quãng đường đi được là \(s\left( {10} \right) = 1100 \Leftrightarrow 1\,\,000k + 50n = 1100.\)
Suy ra \(k = 1,\,\,n = 2\) nên \(s(t) = {t^3} + {t^2}.\)
Vậy quãng đường cần tính là \(s(30) = {30^3} + {30^2} = 27\,\,900\;\,\,({\rm{m)}}.\)
Chọn A.
Câu 14:
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - \left( {m + 1} \right)y = m - 2}\\{2mx + \left( {m - 2} \right)y = 4}\end{array}} \right..\) Biết rằng có hai giá trị của tham số \(m\) là \({m_1},\,\,{m_2}\) để hệ phương trình có nghiệm \(\left( {{x_0};\,\,2} \right).\) Tính \({m_1} + {m_2}\).
 Xem đáp án
Xem đáp án
Vì hệ đã cho có nghiệm \(\left( {{x_0};\,\,2} \right)\) nên ta có \(\left\{ {\begin{array}{*{20}{l}}{{x_0} - \left( {m + 1} \right) \cdot 2 = m - 2}\\{2m{x_0} + \left( {m - 2} \right) \cdot 2 = 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 3m}\\{m{x_0} + m - 2 = 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 3m}\\{3{m^2} + m - 4 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_0} = 3m}\\{\left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = - \frac{4}{3}}\end{array}} \right.}\end{array}} \right.} \right.} \right.\)
Vậy có hai giá trị của \(m\) là \({m_1} = 1,{m_2} = - \frac{4}{3}\) nên ta có \({m_1} + {m_2} = - \frac{1}{3}.\) Chọn A.
Câu 15:
Ông Hưng gửi 320 triệu đồng ở hai ngân hàng X và Y theo phương thức lãi kép. Số tiền thứ nhất gửi ở ngân hàng X với lãi suất 2,1 một quý trong thời gian 15 tháng. Số tiền còn lại gửi ở ngân hàng Y với lãi suất \[0,73\% \] một tháng trong thời gian 9 tháng. Tổng lợi tức đạt được ở hai ngân hàng là \[27\,\,507\,\,768,13\] đồng (chưa làm tròn). Hỏi số tiền ông Hưng lần lượt gửi ở hai ngân hàng X và Y là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi số tiền ông Hưng gửi ở hai ngân hàng X và Y lần lượt là \(x\) và \(y\) triệu đồng.
Khi đó ta có \[\left\{ {\begin{array}{*{20}{l}}{x + y = 320}\\{x{{\left( {1 + 0,021} \right)}^5} + y{{\left( {1 + 0,0073} \right)}^9} = 27,507\,\,768\,\,13 + 320}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 140}\\{y = 180}\end{array}} \right.} \right..\]
Chọn A.
Câu 16:
Có bao nhiêu số nguyên dương \(a\) sao cho tồn tại số thực \(b\) thoả mãn \({2^a} = {3^b}\) và \(a - b < 4\,?\)
 Xem đáp án
Xem đáp án
Ta có \({2^a} = {3^b} \Rightarrow b = a \cdot {\log _3}2\)
\( \Rightarrow a - b < 4 \Leftrightarrow a - a \cdot {\log _3}2 < 4\)\( \Leftrightarrow a\left( {1 - {{\log }_3}2} \right) < 4\)
\( \Leftrightarrow a < {\log _3}\frac{3}{2} < 4 \Leftrightarrow a < \frac{4}{{{{\log }_3}\frac{3}{2}}}\). Do đó \(a \in \left( {0;\frac{4}{{{{\log }_3}\frac{3}{2}}}} \right).\)
Kết hợp điều kiện \(a \in \mathbb{Z} \Rightarrow a \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\, \ldots \,;\,\,10} \right\}.\)
Vậy có 10 giá trị của \(a\) thoả mãn. Chọn B.
Câu 17:
Có bao nhiêu số nguyên \(m\) để hàm số \(f(x) = {x^4} - 2\left( {{m^2} - 3m} \right){x^2} + 3\) đồng biến trên khoảng \(\left( {2\,;\,\, + \infty } \right)?\)
 Xem đáp án
Xem đáp án
Yêu cầu bài toán \( \Leftrightarrow f'\left( x \right) = 4{x^3} - 4\left( {{m^2} - 3m} \right)x \ge 0\,;\,\,\forall x \in \left( {2\,;\,\, + \infty } \right)\)
\( \Leftrightarrow 4x\left( {{x^2} - {m^2} + 3m} \right) \ge 0\,;\,\,\forall x \in \left( {2\,;\,\, + \infty } \right)\)
\( \Leftrightarrow {x^2} - {m^2} + 3m \ge 0 \Leftrightarrow {m^2} - 3m \le {x^2}\,;\,\,\forall x \in \left( {2\,;\,\, + \infty } \right)\)
\( \Rightarrow m \in \left[ { - 1\,;\,\,4} \right].\) Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4} \right\}.\)
Vậy có 6 giá trị của \(m\) thoả mãn yêu cầu bài toán. Chọn B.
Câu 18:
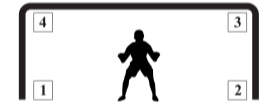
Trong trận đấu bóng đá giữa hai đội U23 Việt Nam và U23 Iraq, trọng tài cho đội Iraq được hưởng một quả đá phạt 11 m. Cầu thủ sút phạt ngẫu nhiên vào một trong bốn vị trí \[1\,;\,\,2\,;\,\,3\,;\,\,4\] và thủ môn bay người cản phá ngẫu nhiên đến một trong bốn vị trí đó với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 hoặc 2 thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 hoặc 4 thì xác suất cản phá thành công là \[50\% .\] Xác suất để cú sút đó không vào lưới là
 Xem đáp án
Xem đáp án
Xét tại vị trí 3: xác suất để cầu thủ đá đúng vị trí 3 là \(\frac{1}{4}.\)
Đây cũng là xác suất thủ môn lao đến vị trị 3 và xác suất để thủ môn bắt được bóng ở vị trí này là \(\frac{1}{2}\), do đó xác suất để bóng không vào lưới là \(\frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{2} = \frac{1}{{32}}.\) Tương tự với vị trí 3.
Xét tại vị trí 1: cũng tương tự tuy nhiên khi cầu thủ sút bóng và thủ môn cùng lao về vị trí này thì thủ môn chắc chắn bắt được bóng, do đó xác suất là \(\frac{1}{4} \cdot \frac{1}{4} = \frac{1}{{16}}.\) Tương tự với vị trí 2.
Vậy xác suất cần tính là \(P = \frac{1}{{32}} \cdot 2 + \frac{1}{{16}} \cdot 2 = \frac{3}{{16}}.\) Chọn B.
Câu 19:
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng \(d:3x - 4y - 1 = 0\) và điểm \(I\left( {1\,;\,\, - 2} \right).\) Gọi \((C)\) là đường tròn có tâm I và cắt đường thẳng \(d\) tại hai điểm \[A\] và \[B\] sao cho tam giác \[IAB\] có diện tích bằng 4. Phương trình đường tròn \((C)\) là
 Xem đáp án
Xem đáp án
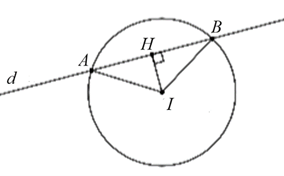
Ta có: \(IH = d\left( {I\,;\,\,d} \right) = 2.\)
\({S_{IAB}} = \frac{1}{2}IH \cdot AB \Rightarrow AB = \frac{{2 \cdot {S_{IAB}}}}{{IH}} = \frac{{2 \cdot 4}}{2} = 4 \Rightarrow AH = 2.\)
\( \Rightarrow R = IA = \sqrt {A{H^2} + I{H^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 .\)
\[ \Rightarrow \left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 8.\] Chọn A.Câu 20:
Cho hình chóp \[S.ABCD\] có đáy \[ABC\] là tam giác vuông tại \(B,\,\,BC = a,\,\,AC = 2a.\) Mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng đáy, \[SAB\] là tam giác đều có trọng tâm \[G.\] Thể tích của khối chóp S.GBC bằng
 Xem đáp án
Xem đáp án
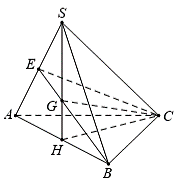
Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot AB\)
Mà \((SAB) \bot (ABC);(SAB) \cap (ABC) = AB \Rightarrow SH \bot (ABC)\)
Ta có \(\frac{{{V_{S.GBC}}}}{{{V_{S.HBC}}}} = \frac{{SG}}{{SH}} = \frac{2}{3} \Rightarrow {V_{S.GBC}} = \frac{2}{3} \cdot \frac{1}{2}{V_{S.ABC}} = \frac{1}{3}{V_{S.ABC}}\)
Lai có \(AB = \sqrt {A{C^2} - B{C^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = \sqrt 3 a\)
Do đó \(SH = AB \cdot \frac{{\sqrt 3 }}{2} = \sqrt 3 a \cdot frac{{\sqrt 3 }}{2} = \frac{{3a}}{2}\)Suy ra \[{V_{S.ABC}} = \frac{1}{3}SH \cdot {S_{ABC}} = \frac{1}{3} \cdot \frac{{3a}}{2} \cdot \frac{{\sqrt 3 a \cdot a}}{2} = \frac{{\sqrt 3 {a^3}}}{4}\]
Vậy thể tích cần tính là \({V_{S.GBC}} = \frac{1}{3} \cdot \frac{{\sqrt 3 {a^3}}}{4} = \frac{{\sqrt 3 }}{{12}}{a^3}.\) Chọn C.
Câu 21:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) là \(f'\left( x \right) = x{\left( {x - 1} \right)^2}\left( {x + 2} \right).\) Khi đó, hàm số \(y = f\left( { - 2x} \right)\) đạt cực đại tại
 Xem đáp án
Xem đáp án
Xét \(f'\left( x \right) = 0 \Leftrightarrow x{\left( {x - 1} \right)^2}\left( {x + 2} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\\{x = - 2}\end{array}} \right..\)
Khi đó, ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau
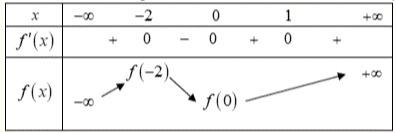
Xét \(y = f\left( { - 2x} \right)\), ta có \(y' = - 2f'\left( { - 2x} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 2x = - 2}\\{ - 2x = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 0}\end{array}} \right.} \right..\)
Khi đó, ta có bảng biến thiên của hàm số \(y = f\left( { - 2x} \right)\) như sau
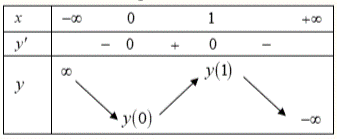
Vậy hàm số \(y = f\left( { - 2x} \right)\) đạt cực đại tại \(x = 1.\) Chọn C.
Câu 22:
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \(x = 2\cos \left( {5t - \frac{\pi }{6}} \right).\) Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimét. Hỏi trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
 Xem đáp án
Xem đáp án
Vị trí cân bằng của vật dao động điều hoà là vị trí vật đứng yên, khi đó \(x = 0.\)
Ta có \(2\cos \left( {5t - \frac{\pi }{6}} \right) = 0\)\( \Leftrightarrow \cos \left( {5t - \frac{\pi }{6}} \right) = 0\)
\( \Leftrightarrow 5t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}\)\( \Leftrightarrow t = \frac{{2\pi }}{{15}} + k\frac{\pi }{5},\,\,k \in \mathbb{Z}\)
Trong khoảng thời gian từ 0 đến 6 giây, tức là \(0 \le t \le 6\)
Hay \(0 \le \frac{{2\pi }}{{15}} + k\frac{\pi }{5} \le 6 \Leftrightarrow - \frac{2}{3} \le k \le \frac{{90 - 2\pi }}{{3\pi }}.\)
Vì \(k \in \mathbb{Z}\) nên \(k \in \left\{ {0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6\,;\,\,7\,;\,\,8} \right\}.\)
Vậy trong khoảng thò̀i gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.
Chọn D.
Câu 23:
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(y' = x{y^2}\) và \(f\left( { - 1} \right) = 1\) thì giá trị \(f\left( 2 \right)\) là
 Xem đáp án
Xem đáp án
Ta có \(f\left( x \right) + x \cdot f'\left( x \right) = 4{x^3} + 4x + 2\)\( \Leftrightarrow x' \cdot f\left( x \right) + x \cdot f'\left( x \right) = 4{x^3} + 4x + 2\)
\( \Leftrightarrow {\left( {x \cdot f'\left( x \right)} \right)^\prime } = 4{x^3} + 4x + 2 \Leftrightarrow x \cdot f\left( x \right) = \int {\left( {4{x^3} + 4x + 2} \right){\rm{d}}x} \)
\[ \Leftrightarrow x \cdot f\left( x \right) = {x^4} + 2{x^2} + 2x + C\,\,\,(*)\]
Thay \(x = 0\) vào (*), ta được \(C = 0 \Rightarrow f\left( x \right) = {x^3} + 2x + 2.\)
Suy ra \(f'\left( x \right) = 3{x^2} + 2\), do đó \(f\left( x \right) = f'\left( x \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1.{\rm{ }}}\\{x = 2}\end{array}} \right.\)
Vậy diện tích cần tính là \(S = \int\limits_0^2 {\left| {{x^3} - 3{x^2} + 2x} \right|{\rm{d}}x} = \frac{1}{2}.\) Chọn C.
Câu 24:
Cho hình lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\), các cạnh bên tạo với đáy góc \(60^\circ .\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
 Xem đáp án
Xem đáp án
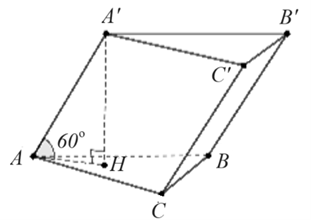
Kẻ \[A'H \bot \left( {ABC} \right)\]
\[ \Rightarrow \left( {A'A,\,\,\left( {ABC} \right)} \right) = \widehat {A'AH} = 60^\circ \]
Xét \(\Delta AHA'\) có \(\sin 60^\circ = \frac{{A'H}}{{AA'}}\)
\( \Leftrightarrow A'H = AA' \cdot \sin 60^\circ = \frac{{a\sqrt 3 }}{2}.\)
Thể tích khối lăng trụ \(ABC.A'B'C'\) là:
\[V = {S_{ABC}} \cdot A'H = \frac{{{a^2}\sqrt 3 }}{4} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{3{a^3}}}{8}.\] Chọn B.Câu 25:
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho ba điểm \(A\left( {1\,;\,\,0\,;\,\,0} \right),\,\,C\left( {0\,;\,\,0\,;\,\,3} \right),\)\(B\left( {0\,;\,\,2\,;\,\,0} \right).\) Tập hợp các điểm \(M\) thỏa mãn MA2 = MB2 + MC2 là mặt cầu có bán kính là
 Xem đáp án
Xem đáp án
Giả sử \(M\left( {x\,;\,\,y\,;\,\,z} \right).\)
Ta có: \(M{A^2} = {\left( {x - 1} \right)^2} + {y^2} + {z^2};\,\,M{B^2} = {x^2} + {\left( {y - 2} \right)^2} + {z^2};\,\,M{C^2} = {x^2} + {y^2} + {\left( {z - 3} \right)^2}.\)
\(M{A^2} = M{B^2} + M{C^2} \Leftrightarrow {\left( {x - 1} \right)^2} + {y^2} + {z^2} = {x^2} + {\left( {y - 2} \right)^2} + {z^2} + {x^2} + {y^2} + {\left( {z - 3} \right)^2}\)\( \Leftrightarrow - 2x + 1 = {\left( {y - 2} \right)^2} + {x^2} + {\left( {z - 3} \right)^2} \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 2.{\rm{ }}\)
Vậy tập hợp các điểm \(M\) thoả mãn \(M{A^2} = M{B^2} + M{C^2}\) là mặt cầu có bán kính là \(R = \sqrt 2 .\)
Chọn D.
Câu 26:
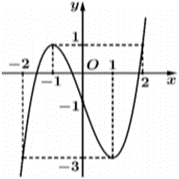
Cho hàm số \(f\left( x \right)\) có đồ thị của \(y = f'\left( x \right)\) là đường cong trong hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {2x - 1} \right) + mx + 3\) có ba điểm cực trị?
 Xem đáp án
Xem đáp án
Xấp xỉ hàm, coi hàm số \(f\left( {2x - 1} \right) \approx f\left( x \right)\).
Khi đó \(g\left( x \right) = f\left( x \right) + mx + 3\), có \[g'\left( x \right) = f'\left( x \right) + m = 0 \Leftrightarrow - m = f'\left( x \right)\].
Yêu cầu bài toán \[ \Leftrightarrow - m = f'\left( x \right)\] có ba nghiệm đơn phân biệt
Dựa vào hình vẽ, ta được \( - 3 < - m < 1 \Leftrightarrow - 1 < m < 3\).
Mà \(m \in \mathbb{Z}\) nên suy ra \(m \in \left\{ {0\,;\,\,1\,;\,\,2} \right\}.\) Chọn B.
Câu 27:
Số nghiệm nguyên của bất phương trình \(\left( {4 \cdot {3^x} + {2^x} - {6^x} - 4} \right)\left[ {\log \left( {x + 2} \right) - 2} \right] \ge 0\) là
 Xem đáp án
Xem đáp án
Điều kiện: \(x > - 2.\)
\(\left( {4 \cdot {3^x} + {2^x} - {6^x} - 4} \right)\left[ {\log \left( {x + 2} \right) - 2} \right] \ge 0\)
\( \Leftrightarrow \left[ {4\left( {{3^x} - 1} \right) - {2^x}\left( {{3^x} - 1} \right)} \right]\left[ {\log \left( {x + 2} \right) - 2} \right] \ge 0\)
\( \Leftrightarrow \left( {{3^x} - 1} \right)\left( {4 - {2^x}} \right)\left[ {\log \left( {x + 2} \right) - 2} \right] \ge 0\)
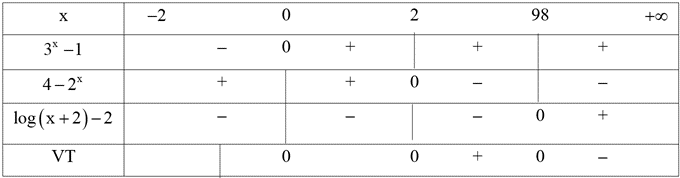
Từ bảng xét dấu ta có: \(\left( {{3^x} - 1} \right)\left( {4 - {2^x}} \right)\left[ {\log \left( {x + 2} \right) - 2} \right] \ge 0 \Leftrightarrow x \in \left( { - 2\,;\,\,0} \right] \cup \left[ {2\,;\,\,98} \right].\)
Mà \[x \in \mathbb{Z} \Rightarrow x \in \left\{ { - 1\,;\,\,0\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\, \ldots \,;\,\,97\,;\,\,98} \right\}.\]
Vậy số nghiệm nguyên của bất phương trình đã cho là 99. Chọn B.
Câu 28:
Cho hàm số \(f\left( x \right) = m\sqrt {x - 1} \) (\(m\) là tham số thực khác 0). Gọi \({m_1},\,\,{m_2}\) là hai giá trị của \(m\) thỏa mãn \[{\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10.\] Giá trị của \({m_1} + {m_2}\) bằng
 Xem đáp án
Xem đáp án
Ta có \(f'\left( x \right) = m \cdot \frac{1}{{2\sqrt {x - 1} }}\).
Do \(m \ne 0\) nên \(f'\left( x \right) \ne 0\) và có dấu không thay đổi \(\forall x \in \left( {1\,;\,\, + \infty } \right).\)
TH1: Nếu \(m > 0\) thì \(f'\left( x \right) > 0\,,\,\,\forall x \in \left[ {2;\,\,5} \right].\)
Do đó \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(2) = m\,;\,\,{\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(5) = 2m.\)
Suy ra \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10\)
\( \Leftrightarrow m + 2m = {m^2} - 10\)\( \Leftrightarrow {m^2} - 3m - 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m_1} = - 2}\\{{m_2} = 5}\end{array}} \right.\).
Do \(m > 0\) nên nhận \({m_2} = 5.\)
TH2: Nếu \(m < 0\) thì \(f'\left( x \right) < 0\,,\,\,\forall x \in \left[ {2;\,\,5} \right].\)
Do đó \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(5) = 2m\,;\,\,{\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(2) = m.\)
Suy ra \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10\)
\( \Leftrightarrow 2m + m = {m^2} - 10\)\( \Leftrightarrow {m^2} - 3m - 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m_1} = - 2}\\{{m_2} = 5}\end{array}} \right.\).
Do \(m < 0\) nên nhận \({m_1} = - 2.\)
Vậy \({m_1} + {m_2} = 3.\) Chọn A.
Câu 29:
Trong không gian \[Oxyz,\] cho mặt phẳng \(\left( Q \right)\) song song với mặt phẳng \(\left( P \right):2x - 2y + z - 7 = 0.\) Biết mặt phẳng \(\left( Q \right)\) cắt mặt cầu \(\left( S \right):{x^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 25\) theo một đường tròn có bán kính \(r = 3.\) Khi đó mặt phẳng \(\left( Q \right)\) có phương trình là
 Xem đáp án
Xem đáp án
Do \(\left( Q \right)\,{\rm{//}}\,\left( P \right):2x - 2y + z - 7 = 0\), suy ra \(\left( Q \right):2x - 2y + z + m = 0,\,\,\left( {m \ne - 7} \right).\)
Ta có \(\left( S \right):{x^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 25\) có tâm \(I\left( {0\,;\,\,2\,;\,\, - 1} \right)\) bán kính \(R = 5.\)
Gọi \(h = d\left( {I;\,\,\left( Q \right)} \right) = \frac{{\left| {2 \cdot 0 - 2 \cdot 2 - 1 + m} \right|}}{{\sqrt {4 + 4 + 1} }} = \frac{{\left| {m - 5} \right|}}{3}.\)
Do \((Q)\) cắt mặt cầu \((S)\) theo một đường tròn có bán kính \(r = 3\), suy ra \({R^2} = {r^2} + {h^2}\)
\( \Leftrightarrow 25 = 9 + \frac{{{{\left( {m - 5} \right)}^2}}}{9} \Leftrightarrow {\left( {m - 5} \right)^2} = 144 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m - 5 = 12}\\{m - 5 = - 12}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 17}\\{m = - 7{\rm{ (loai) }}}\end{array}} \right.} \right.\)
Vậy mặt phẳng \(\left( Q \right)\) có phương trình là \(2x - 2y + z + 17 = 0.\) Chọn D.
Câu 30:
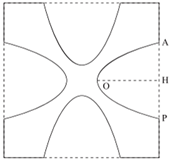
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng \(10\;\,{\rm{cm}}\) bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình vẽ. Biết \(AB = 5\;{\rm{cm}}\,,\,\,OH = 4\;{\rm{cm}}.\) Diện tích bề mặt hoa văn đó là
 Xem đáp án
Xem đáp án
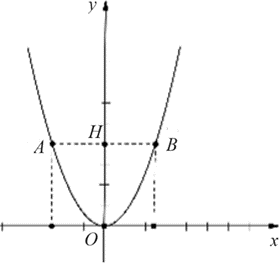
Chọn hệ trục tọa độ sao cho \(O\) là gốc tọa độ.
\(OH \in Oy\,;\,\,Ox \bot OH = O\) chiều dương hướng từ \(A\) đến \(B\) nên \(B\left( {\frac{5}{2};4} \right).\)
Giả sử parabol \(\left( P \right)\) đi qua \(O\) có dạng \(y = a{x^2} + bx + c\)
Ta có hệ phương trình
\(\left\{ {\begin{array}{*{20}{l}}{O \in \left( P \right)}\\{\frac{{ - b}}{{2a}} = 0}\\{B \in \left( P \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{c = 0;b = 0}\\{a = \frac{{16}}{{25}}}\end{array} \Rightarrow y = \frac{{16}}{{25}}{x^2}} \right.} \right..\)Gọi diện tích hình phẳng giới hạn các đường \(y = \frac{{16}}{{25}}{x^2},\,\,y = 4,\,\,x = - \frac{5}{2};\,\,x = \frac{5}{2}\) là \({S_1}.\)
Ta có \[{S_1} = \int\limits_{ - 2,5}^{2,5} {\left( {4 - \frac{{16}}{{25}}{x^2}} \right)dx} = \frac{{40}}{3}\;\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\]
Diện tích hoa văn là \(S = {10^2} - \frac{{40}}{3} \cdot 4 = \frac{{140}}{3}\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\). Chọn B.
Câu 31:
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở \[A,\,\,B\] khác tiếp điểm. Độ dài đoạn thẳng \[AB\] là
 Xem đáp án
Xem đáp án
Ta có \(y' = - {x^3} + 4x\,;\,\,y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm \,2}\end{array}} \right.\).
Bảng biến thiên:
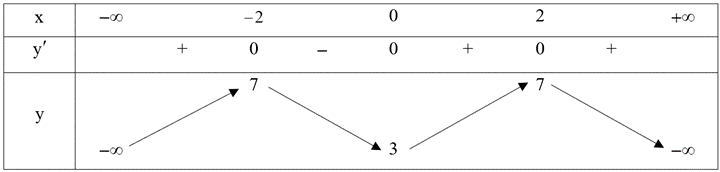
Từ bảng biến thiên suy ra điểm cực tiểu của đồ thị hàm số là \(M\left( {0\,;\,\,3} \right).\)
Tiếp tuyến của đồ thị tại điểm cực tiểu là đường thẳng \(y = 3.\)
Phương trình hoành độ giao điểm của đồ thị và tiếp tuyến là:
\( - \frac{1}{4}{x^4} + 2{x^2} + 3 = 3 \Leftrightarrow - \frac{1}{4}{x^4} + 2{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm 2\sqrt 2 }\end{array}} \right.\)
\( \Rightarrow A\left( { - 2\sqrt 2 \,;\,\,3} \right)\,;\,\,B\left( {2\sqrt 2 \,;\,\,3} \right) \Rightarrow AB = 4\sqrt 2 .\) Chọn D.
Câu 32:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a,\,\,SA\] vuông góc với đáy và \(SA = a.\) Điểm \(M\) nằm trên cạnh \[SA\] sao cho \(\frac{{SM}}{{SA}} = k.\) Khi mặt phẳng \(\left( {BMC} \right)\) chia khối chóp \[S.ABCD\] thành hai phần có thể tích bằng nhau thì giá trị của \(k\) bằng
 Xem đáp án
Xem đáp án
Vì \(BC\,{\rm{//}}\,AD\) nên mặt phẳng \(\left( {BMC} \right)\) cắt \((SAD)\) theo đoạn thẳng \(MN\,{\rm{//}}\,AD\,\,\left( {N \in SD} \right)\)
\(\frac{{{V_{S.BMC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}} = k\); \(\frac{{{V_{S.MNC}}}}{{{V_{S.ADC}}}} = \frac{{SM}}{{SA}} \cdot \frac{{SN}}{{SD}} = {k^2}\)
\( \Rightarrow {V_{S.MNC}} = {k^2} \cdot {V_{S.ADC}} = \frac{{{k^2}}}{2} \cdot {V_{S.ABCD}}\)\( \Rightarrow {V_{S.MBCN}} = \left( {\frac{k}{2} + \frac{{{k^2}}}{2}} \right) \cdot {V_{S.ABCD}}\).
Để \(\left( {BMC} \right)\) chia khối chóp \[S.ABCD\] thành hai phần có thể tích bằng nhau thì
\(\frac{k}{2} + \frac{{{k^2}}}{2} = \frac{1}{2} \Leftrightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \frac{{ - 1 + \sqrt 5 }}{2}\,\,\left( {k > 0} \right).\) Chọn B.
Câu 33:
Trong không gian \[Oxyz,\] cho đường thẳng \(d:\frac{{x + 1}}{{ - 2}} = \frac{y}{1} = \frac{{z - 1}}{1}\) và điểm \(A\left( {1\,;\,\,2\,;\,\,3} \right).\) Mặt phẳng \(\left( P \right)\) chứa \(d\) sao cho khoảng cách từ \(A\) đến \(\left( P \right)\) lớn nhất. Khi đó một vectơ pháp tuyến của \(\left( P \right)\) có toạ độ là
 Xem đáp án
Xem đáp án
Gọi \[H,\,\,K\] lần lượt là hình chiếu của \(A\) trên \(d\,,\,\,\left( P \right).\)
Khi đó \(d\left( {A;\,\,\left( P \right)} \right) = AK \le AH.\) Dấu xảy ra khi \(H \equiv K.\)
\(H \in d \Rightarrow H\left( { - 2t - 1\,;\,\,t\,;\,\,t + 1} \right) \Rightarrow \overrightarrow {AH} = \left( { - 2t - 2\,;\,\,t - 2\,;\,\,t - 2} \right)\)
\({\rm{M\`a }}\overrightarrow {AH} \bot {\vec u_d}{\rm{ n\^e n }} - 2\left( { - 2t - 2} \right) + 1\left( {t - 2} \right) + 1\left( {t - 2} \right) = 0\)
\( \Leftrightarrow 4t + 4 + 2t - 4 = 0 \Leftrightarrow t = 0 \Rightarrow H\left( { - 1\,;\,\,0\,;\,\,1} \right).\)
Do đó \[{\vec n_{\left( P \right)}} = k \cdot \overrightarrow {AH} = k \cdot \left( { - 2\,;\,\, - 2\,;\,\, - 2} \right) = \left( {1\,;\,\,1\,;\,\,1} \right).\] Chọn B.
Câu 34:
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1.\) Có bao nhiêu giá trị nguyên của \(m\) để giá trị nhỏ nhất của hàm số \[y = \left| {f\left( {2\sin x + 1} \right) + m} \right|\] không vượt quá 10?
 Xem đáp án
Xem đáp án
Đặt \(t = 2\sin x + 1\,,\,\,t \in \left[ { - 1\,;\,\,3} \right]\)
Xét hàm số \(g(t) = f(t) + m = {t^3} - 3t + 1 + m\,,\,\,t \in \left[ { - 1\,;\,\,3} \right]\)
\(g'(t) = 3{t^2} - 3 = 0 \Leftrightarrow t = \pm 1\)
Suy ra \({\max _{\left[ { - 1\,;\,\,3} \right]}}g(t) = g(3) = m + 19\,,\,\,{\min _{\left[ { - 1\,;\,\,3} \right]}}g(t) = g(1) = m - 1\)
TH1: Nếu \(m + 19 > m - 1 > 0\,\,\left( {m > 1} \right)\)
Để thoả mãn yêu cầu bài toán thì \(m - 1 \le 10 \Rightarrow m \le 11 \Rightarrow 1 < m \le 11\) (1)
TH2: Nếu \(0 > m + 19 > m - 1\,\,\left( {m < - 19} \right)\)
Để thoả mãn yêu cầu bài toán thì \(m + 19 \ge - 10 \Leftrightarrow m \ge - 29 \Rightarrow - 29 \le m < - 19\) (2)
TH3: Nếu \(m - 1 \le 0 \le m + 19 \Leftrightarrow - 19 \le m \le 1\) thì \(\min y = 0\) (hiển nhiên đúng) (3)
Từ (1), (2), (3) suy ra \( - 29 \le m \le 11\).
Vậy có 41 số nguyên thoả mãn. Chọn B.
Câu 35:
Một bình nước dạng hình nón (không có đáy) đựng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là \(18\pi \,\,d{m^3}.\) Biết khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa khối cầu chìm trong nước. Thể tích nước còn lại trong bình là
 Xem đáp án
Xem đáp án
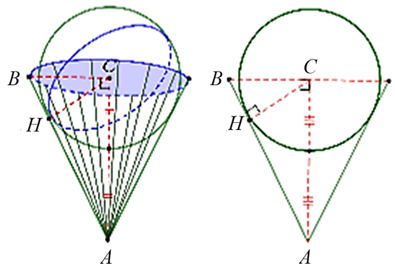
Vì đúng một nửa khối cầu chìm trong nước nên thể tích khối cầu gấp 2 lần thể tích nước tràn ra ngoài.
Gọi bán kính khối cầu là \(R,\) lúc đó: \(\frac{4}{3}\pi {R^3} = 36\pi \Leftrightarrow {R^3} = 27.\)
Xét tam giác \[ABC\] có \[AC\] là chiều cao bình nước nên \(AC = 2R\) (vì khối cầu có đường kính bằng chiều cao của bình nước).
Trong tam giác \[ABC\] có: \(\frac{1}{{C{H^2}}} = \frac{1}{{C{A^2}}} + \frac{1}{{C{B^2}}} \Leftrightarrow \frac{1}{{{R^2}}} = \frac{1}{{4{R^2}}} + \frac{1}{{C{B^2}}} \Leftrightarrow C{B^2} = \frac{{4{R^2}}}{3}.\)
Thể tích khối nón là: \({V_n} = \frac{1}{3}\pi \cdot C{B^2} \cdot AC = \frac{1}{3}\pi \cdot \frac{{4{R^2}}}{3} \cdot 2R = \frac{{8\pi }}{9} \cdot {R^3} = 24\pi \,\,\left( {d{m^3}} \right).\)
Chọn D.
Câu 36:
Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
 Xem đáp án
Xem đáp án
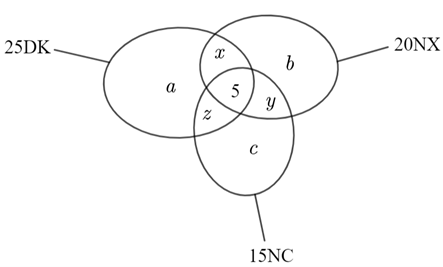
Gọi \[a,\,\,b,\,\,c\] theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao;
\[x\] là số học sinh chỉ thi hai môn điền kinh và nhảy xa;
\[y\] là số học sinh chỉ thi hai môn nhảy xa và nhảy cao;
\[z\] là số học sinh chỉ thi hai môn điền kinh và nhảy cao.
Số em thi ít nhất một môn là \(45 - 7 = 38\) (học sinh).
Dựa vào biểu đồ Ven ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + x + z + 5 = 25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)}\\{b + x + y + 5 = 20\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)}\\{c + y + z + 5 = 15\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)}\\{x + y + z + a + b + c + 5 = 38\,\,\,\,\,(4)}\end{array}} \right.\)
Cộng vế với vế của \[(1),\,\,(2),\,\,(3)\] ta được: \(a + b + c + 2\left( {x + y + z} \right) + 15 = 60\) (5)
Từ (4), (5) ta có: \(a + b + c + 2\left( {38 - 5 - a - b - c} \right) + 15 = 60 \Leftrightarrow a + b + c = 21.\)
Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.
Đáp án: 21.
Câu 37:
Cho dãy số \(\left( {{u_n}} \right),\,\,n \in \mathbb{N}*,\) thỏa mãn điều kiện \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 3}\\{{u_{n + 1}} = - \frac{{{u_n}}}{5}}\end{array}} \right..\) Gọi \(S = {u_1} + {u_2} + {u_3} + \ldots + {u_n}\) là tổng \(n\) số hạng đầu tiên của dãy số đã cho. Khi đó \(\lim {S_n}\) bằng
 Xem đáp án
Xem đáp án
Ta có \(\frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{ - \frac{{{u_n}}}{5}}}{{{u_n}}} = - \frac{1}{5}\) do đó dãy \(\left( {{u_n}} \right),\,\,n \in {\mathbb{N}^*}\) là một cấp số nhân lùi vô hạn có \({u_1} = 3,q = - \frac{1}{5}.\)
Suy ra \(\lim {S_n} = \frac{{{u_1}}}{{1 - q}} = \frac{3}{{1 + \frac{1}{5}}} = \frac{5}{2}.\)
Đáp án: \(\frac{5}{2}.\)
Câu 38:
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh a. Một khối nón có đỉnh là tâm của hình vuông \(ABCD\) và đáy là hình tròn nội tiếp hình vuông \(A'B'C'D'.\) Kết quả tính diện tích toàn phần \({S_{tp}}\) của khối nón đó có dạng bằng \(\frac{{\pi {a^2}}}{4}\left( {\sqrt b + c} \right)\) với \(b\) và \(c\) là hai số nguyên dương và \(b > 1.\) Tính \[bc.\]
 Xem đáp án
Xem đáp án
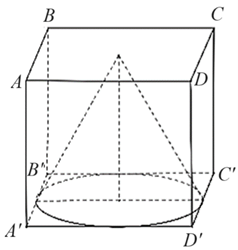
Ta có bán kính hình nón \(r = \frac{a}{2}\), đường cao \(h = a,\) đường sinh \(\ell = \frac{{a\sqrt 5 }}{2}.\)
Diện tích toàn phần là:
\({S_{tp}} = \pi r\ell + \pi {r^2} = \pi \frac{{{a^2}\sqrt 5 }}{4} + \pi \frac{{{a^2}}}{4} = \frac{{\pi {a^2}}}{4}\left( {\sqrt 5 + 1} \right) \Rightarrow b = 5\,,\,\,c = 1.\)Vậy \(bc = 5.\)
Đáp án: 5.Câu 39:
Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26. Bạn Hải rút ngẫu nhiên cùng một lúc ba tấm thẻ. Hỏi có bao nhiêu cách rút sao cho bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị?
 Xem đáp án
Xem đáp án
Số cách rút được 3 thẻ bất kì là \(C_{26}^3\).
Số cách rút được 3 thẻ có đúng 2 số tự nhiên liên tiếp:
Chọn 2 số tự nhiên liên tiếp: \[\left\{ {1\,;\,\,2} \right\}\,;\,\,\left\{ {2\,;\,\,3} \right\}\,;\,\, \ldots \,;\,\,\left\{ {25\,;\,\,26} \right\}\].
TH1: Chọn 2 thẻ là \[\left\{ {1\,;\,\,2} \right\}\] hoặc \[\left\{ {25\,;\,\,26} \right\}\], có 2 cách.
Thẻ còn lại không được là 3 (hoặc 24): \[26 - 3 = 23\] (cách) \( \Rightarrow 2 \cdot 23 = 46\) (cách).
TH2: Chọn 2 thẻ là \[\left\{ {2\,;\,\,3} \right\}\,;\,\,\left\{ {3\,;\,\,3} \right\}\,;\,\, \ldots ;\left\{ {24\,;\,\,25} \right\}\], có 23 cách.
Thẻ còn lại chỉ có: \[26 - 4 = 22\] (cách). Khi đó, \[23 \cdot 22 = 506\] (cách).
Số cách rút 3 thẻ trong đó có 3 số tự nhiên liên tiếp:
\[\left\{ {1\,;\,\,2\,;\,\,3} \right\}\,;\,\,\left\{ {2\,;\,\,3\,;\,\,4} \right\}\,;\,\, \ldots \,;\,\,\left\{ {24\,;\,\,25\,;\,\,26} \right\}\], có 24 cách.
Vậy có: \(C_{26}^3 - 46 - 506 - 24 = 2\,\,024\) (cách).
Đáp án: 2024.
Câu 40:
Một anh kỹ sư muốn tạo ra 1 cái lu hình trụ có diện tích bề mặt (không tính hai mặt đáy) là lớn nhất. Bề mặt lu được quấn bởi mảnh tôn hình chữ nhật có chu vi \(120\;\,\,{\rm{cm}}.\) Gọi chiều dài của hình chữ nhật là a, chiều rộng của hình chữ nhật là \[b.\] Tính \(P = {a^2} + 3b.\)
 Xem đáp án
Xem đáp án
Theo bài ra, ta có \(2a + 2b = 120 \Leftrightarrow a + b = 60.\)
Diện tích xung quanh của hình trụ chính là diện tích của hình chữ nhật.
Khi đó \({S_{xq}} = ab \le {\left( {\frac{{a + b}}{2}} \right)^2} = \frac{{{{60}^2}}}{4} = 900\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Dấu bằng xảy ra khi và chỉ khi: \(a = b = 30.\)
Đáp án: 990.
Câu 41:
Có bao nhiêu số nguyên của \(m\) thuộc đoạn \(\left[ { - 100\,;\,\,100} \right]\) để đồ thị hàm số \(y = \frac{1}{{\left( {x - m} \right)\sqrt {2x - {x^2}} }}\) có đúng hai đường tiệm cận?
 Xem đáp án
Xem đáp án
Ta có điều kiện xác định là \(\left\{ {\begin{array}{*{20}{l}}{x \ne m}\\{x \in \left( {0\,;\,\,2} \right)}\end{array}} \right.\), khi đó đồ thị hàm số sẽ không có tiệm cận ngang.
Ta có \(\mathop {\lim }\limits_{x \to {0^ + }} y = \infty \,,\,\,\mathop {\lim }\limits_{x \to {2^ - }} y = \infty \)
Suy ra \(x = 0\,,\,\,x = 2\) là hai đường tiệm cận đứng.
Vậy để đồ thị hàm số có đúng hai đường tiệm cận thì \(\left[ {\begin{array}{*{20}{l}}{m \le 0}\\{m \ge 2}\end{array}} \right.\), theo bài \(m\) thuộc đoạn \(\left[ { - 100\,;\,\,100} \right].\)
Vậy có 200 số nguyên \(m\) thoả mãn đầu bài.
Đáp án: 200.
Câu 42:
Cho \[x,\,\,y\] là các số thực dương thỏa mãn \({\log _5}x + {\log _5}y \ge {\log _5}\left( {{x^2} + y} \right).\) Biết giá trị nhỏ nhất của biểu thức \(P = 2x + y\) là \(a\sqrt b + c\), trong đó \[a,\,\,b,\,\,c\] là các số tự nhiên và \(a > 1.\) Giá trị biểu thức \(Q = abc\) là
 Xem đáp án
Xem đáp án
Ta có \({\log _5}x + {\log _5}y \ge {\log _5}\left( {{x^2} + y} \right) \Leftrightarrow {\log _5}(xy) \ge {\log _5}\left( {{x^2} + y} \right)\)
\( \Leftrightarrow xy \ge {x^2} + y \Leftrightarrow y\left( {x - 1} \right) \ge {x^2} \Leftrightarrow y \ge \frac{{{x^2}}}{{x - 1}}\) với \(x > 1.\)
Do đó \(P = 2x + y \ge 2x + \frac{{{x^2}}}{{x - 1}} = 2x + \frac{{{x^2} - 1 + 1}}{{x - 1}} = 2x + x + 1 + \frac{1}{{x - 1}}\)
\( = 3x + 1 + \frac{1}{{x - 1}} = 3\left( {x - 1} \right) + \frac{1}{{x - 1}} + 4 \ge 2\sqrt {3\left( {x - 1} \right) \cdot \frac{1}{{x - 1}}} + 4 = 2\sqrt 3 + 4.\)
Vậy \(\min P = 2\sqrt 3 + 4 \Rightarrow a = 2\,;\,\,b = 3\,;\,\,c = 4 \Rightarrow Q = abc = 24.\)
Đáp án: 24.
Câu 43:
Cho số phức \(z\) thỏa mãn \[\left| {\bar z} \right| = \left| {z + 2i} \right|.\] Giá trị nhỏ nhất của biểu thức \(P = \left| {z - i} \right| + \left| {z - 4} \right|\) là
 Xem đáp án
Xem đáp án
Gọi \(M\left( {x\,;\,\,y} \right)\) là điểm biểu diễn số phức \[z.\]
Ta có \(\left| {\bar z} \right| = \left| {z + 2i} \right| \Leftrightarrow y + 1 = 0\), tức biểu diễn hình học của số phức thoả mãn giả thiết là đường thẳng \(y + 1 = 0.\) Xét điểm \(A\left( {0\,;\,\,1} \right)\) và \(B\left( {4\,;\,\,0} \right)\) thì \(P = \left| {z - i} \right| + \left| {z - 4} \right| = MA + MB.\)
Dễ thấy \[A,\,\,B\] cùng phía với đường thẳng \(y + 1 = 0\) nên \(MA + MB\) nhỏ nhất bằng \(BA'\) trong đó \(A'\left( {0\,;\,\, - 3} \right)\) đối xứng với \(A\) qua đường thẳng \(y + 1 = 0.\)
Do đó \(MA + MB\) nhỏ nhất bằng \(BA' = 5.\)
Đáp án: 5.
Câu 44:
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - \ln 2\,;\,\,\ln 2} \right]\) và thỏa mãn \(f\left( x \right) + f\left( { - x} \right) = \frac{1}{{{e^x} + 1}}.\)
Biết \(\int\limits_{ - \ln 2}^{\ln 2} {f\left( x \right)dx} = a\ln 2 + b\ln 3\,\,\left( {a,\,\,b \in \mathbb{Q}} \right).\) Tính \(P = a + b\).
 Xem đáp án
Xem đáp án
Gọi \(I = \int\limits_{ - \ln 2}^{\ln 2} {f\left( x \right)dx} .\) Đặt \(t = - x \Rightarrow {\rm{d}}t = - {\rm{d}}x.\)
Đổi cận: \(\left\{ \begin{array}{l}x = - \ln 2 \Rightarrow t = \ln 2\\x = \ln 2 \Rightarrow t = - \ln 2.\end{array} \right.\)
Ta được \[I = - \int\limits_{\ln 2}^{ - \ln 2} {f\left( { - t} \right)dt} = - \int\limits_{ - \ln 2}^{\ln 2} {f\left( { - t} \right)dt} = \int\limits_{ - \ln 2}^{\ln 2} {f\left( { - x} \right)dx} .\]
Khi đó ta có: \[2I = - \int\limits_{ - \ln 2}^{\ln 2} {f\left( x \right)dx} {\rm{ + }}\int\limits_{ - \ln 2}^{\ln 2} {f\left( { - x} \right)dx} = \int\limits_{ - \ln 2}^{\ln 2} {\left[ {f\left( x \right) + f\left( { - x} \right)} \right]dx} = \int\limits_{ - \ln 2}^{\ln 2} {\frac{1}{{{e^x} + 1}}dx.} \]
Xét \(\int\limits_{ - \ln 2}^{\ln 2} {\frac{1}{{{e^x} + 1}}dx.} \) Đặt \(u = {e^x} \Rightarrow {\rm{d}}u = {e^x}\;{\rm{d}}x\)
Đổi cận: \(\left\{ \begin{array}{l}x = - \ln 2 \Rightarrow u = \frac{1}{2}\\x = \ln 2 \Rightarrow u = 2\end{array} \right.\).
Ta được \(\int\limits_{ - \ln 2}^{\ln 2} {\frac{1}{{{e^x} + 1}}dx} = \int\limits_{ - \ln 2}^{\ln 2} {\frac{{{e^x}}}{{{e^x}\left( {{e^x} + 1} \right)}}dx} = \int\limits_{\frac{1}{2}}^2 {\frac{1}{{u\left( {u + 1} \right)}}du} \)
\( = \int\limits_{\frac{1}{2}}^2 {\left( {\frac{1}{u} - \frac{1}{{u + 1}}} \right)du} = \left. {\left( {\ln \left| u \right| - \ln \left| {u + 1} \right|} \right)} \right|_{\frac{1}{2}}^2 = \ln 2\).
Vậy ta có \(a = \frac{1}{2},\,\,b = 0 \Rightarrow a + b = \frac{1}{2}.\)
Đáp án: \(\frac{1}{2}.\)
Câu 45:
Cường độ một trận động đất được cho bởi công thức \(M = \log A - \log {A_0},\) với \[A\] là biên độ rung chấn tối đa là \({A_0}\) là hằng số. Đầu thế kỷ XX, một trận động đất ở San Francisco có cường độ đo được là 8 độ Richter. Trong cùng năm đó, trận động đất khác ở Nhật Bản có cường độ đo được 6 độ Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần biên độ trận động đất ở Nhật Bản?
 Xem đáp án
Xem đáp án
Gọi \[A\] là biên độ trận động đất ở San Francisco và \[B\] là biên độ trận động đất ở Nhật Bản.
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\log A - \log {A_0} = 8 \Leftrightarrow \log \frac{A}{{{A_0}}} = 8}\\{\log B - \log {A_0} = 6 \Leftrightarrow \log \frac{B}{{{A_0}}} = 6}\end{array}} \right..\)
Suy ra \(\log \frac{A}{{{A_0}}} - \log \frac{B}{{{A_0}}} = 8 - 6 \Leftrightarrow \log \left( {\frac{A}{{{A_0}}}:\frac{B}{{{A_0}}}} \right) = 2 \Leftrightarrow \log \frac{A}{B} = 2 \Leftrightarrow \frac{A}{B} = {10^2} = 100.\)
Đáp án: 100.
Câu 46:
Trong tập các số phức, phương trình \({z^2} - 6z + m = 0,m \in \mathbb{R}.\) Gọi \({m_0}\) là một giá trị \(m\) để phương trình có hai nghiệm phân biệt \({z_1},\,\,{z_2}\) thỏa mãn \({z_1},\overline {{z_1}} = {z_2} \cdot \overline {{z_2}} .\) Hỏi trong khoảng \(\left( {0\,;\,\,20} \right)\) có bao nhiêu giá trị \({m_0} \in \mathbb{N}?\)
 Xem đáp án
Xem đáp án
Để phương trình \({z^2} - 6z + m = 0\) có hai nghiệm phân biệt \({z_1},\,\,{z_2}\) thỏa mãn \({z_1} \cdot \overline {{z_1}} = {z_2} \cdot \overline {{z_2}} \) thì
\[\left[ \begin{array}{l}\left\{ \begin{array}{l}\Delta < 0 \Leftrightarrow {6^2} - 4m < 0 \Leftrightarrow m > 9\\{z_1} \cdot \overline {{z_1}} = {z_2} \cdot \overline {{z_2}} \Leftrightarrow {z_1},\,\,{z_2} = {z_2} \cdot {z_1}\,\,({\rm{TM}})\end{array} \right.\\\left\{ \begin{array}{l}\Delta > 0 \Leftrightarrow {6^2} - 4m > 0 \Leftrightarrow m < 9 \Leftrightarrow m > 9\\{z_1} \cdot \overline {{z_1}} = {z_2} \cdot \overline {{z_2}} \Leftrightarrow z_1^2 = z_2^2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{z_1} = {z_2}\,\,(\;{\rm{L}})}\\{{z_1} = - {z_2} \Leftrightarrow {z_1} + {z_2} = 0 \Rightarrow 3 = 0\,\,(\;{\rm{L}})}\end{array}} \right.\end{array} \right.\end{array} \right.\]
Mà trong khoảng \(\left( {0\,;\,\,20} \right)\) và \({m_0} \in \mathbb{N}\) nên có 10 giá trị \({m_0}\) thoả mãn.
Đáp án: 10.
Câu 47:
Trong không gian \[Oxyz,\] cho đường thẳng \(d:\frac{{x + 1}}{2} = \frac{y}{{ - 1}} = \frac{{z - 1}}{1}\) cắt mặt phẳng \(\left( P \right):x - 2y - z - 1 = 0\) tại điểm \[M.\] Mặt cầu \(\left( S \right)\) có tâm \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) với \(a > 0\) thuộc đường thẳng \(d\) và tiếp xúc với mặt phẳng \(\left( P \right)\) tại điểm \[A.\] Biết rằng diện tích tam giác \[IAM\] bằng \(12\sqrt 3 .\) Tổng \(a + b + c\) bằng
 Xem đáp án
Xem đáp án
Đường thẳng \(d\) có vectơ chỉ phương là \(\vec u = \left( {2\,;\,\, - 1\,;\,\,1} \right)\) và mặt phẳng \((P)\) có vectơ pháp tuyến là \(\vec n = \left( {1\,;\,\, - 2\,;\,\, - 1} \right).\)
Gọi \(\alpha \) là góc giữa đường thẳng \(d\) và mặt phẳng \((P)\) ta có \(\sin \alpha = \frac{{\left| {\vec n \cdot \vec u} \right|}}{{\left| {\vec n} \right| \cdot \left| {\vec u} \right|}} = \frac{1}{2} \Rightarrow \alpha = 30^\circ .\)
Đặt \(IA = x\) thì ta sẽ có \(MA = IA \cdot \cot 30^\circ = x\sqrt 3 .\)
Diện tích của tam giác \[IAM\] bằng:
\({S_{IAM}} = \frac{1}{2}IA \cdot AM = \frac{1}{2} \cdot x \cdot x\sqrt 3 = 12\sqrt 3 \Rightarrow x = \sqrt {24} .\)Do \(I \in d \Rightarrow I\left( { - 1 + 2t\,;\,\, - t\,;\,\,1 + t} \right)\), điều kiện \( - 1 + 2t > 0 \Leftrightarrow t > \frac{1}{2}.\)
Khi đó \[d\left( {I;\,\,\left( P \right)} \right) = IA = \frac{{\left| { - 1 + 2t + 2t - \left( {1 + t} \right) - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\left| {3t - 3} \right|}}{{\sqrt 6 }} = 2\sqrt 6 \]
\[ \Leftrightarrow 3\left| {t - 1} \right| = 12 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t - 1 = 4}\\{t - 1 = - 4}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 5{\rm{ (TM) }}}\\{t = - 3{\rm{ (L) }}}\end{array}} \right.} \right.\].
Với \[t = 5 \Rightarrow I\left( {9\,;\,\, - 5\,;\,\,6} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 9}\\{b = - 5.}\\{c = 6}\end{array}} \right.\] Vậy \[a + b + c = 10.\]
Câu 48:
 Xem đáp án
Xem đáp án
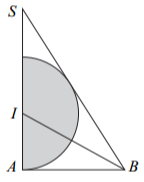
Đặt \(SA = h\).
\(\Delta SAB\) vuông tại \(A \Rightarrow AB = \frac{{SA}}{{\tan {{60}^0}}} = \frac{h}{{\sqrt 3 }}\).
\(\Delta IAB\) vuông tại \(A \Rightarrow \tan \widehat {IBA} = \frac{{IA}}{{AB}} \Rightarrow IA = \frac{h}{3}\).
Khi quay \(\Delta SAB\) quanh trục SA, ta được khối nón có chiều cao \(h,\,\,r = \frac{h}{{\sqrt 3 }}\) và quay nửa đường tròn quanh trục \[SA,\] ta được khối cầu có bán kính \(R = \frac{h}{3}\).
Ta có \({V_1} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {\left( {\frac{h}{{\sqrt 3 }}} \right)^2} \cdot h = \frac{{\pi {h^3}}}{9}\); \({V_2} = \frac{4}{3}\pi {R^2} = \frac{4}{3}\pi {\left( {\frac{h}{3}} \right)^3} = \frac{{4\pi {h^3}}}{{81}}\)
\( \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{9}{4}\).
Đáp án: \(\frac{9}{4}.\)
Câu 49:
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Gọi \(\alpha \) là góc giữa đường thẳng \(A'B\) và mặt phẳng \(\left( {BB'D'D} \right).\) Tính \(\sin \alpha \).
 Xem đáp án
Xem đáp án
Chọn hệ trục toạ độ Oxyz với \[A \equiv O\left( {0\,;\,\,0\,;\,\,0} \right),\,\,B\left( {a\,;\,\,0\,;\,\,0} \right),\,\,C\left( {a\,;\,\,a\,;\,\,0} \right),\,\,D\left( {0\,;\,\,a\,;\,\,0} \right),\]\[\,\,A'\left( {0\,;\,0\,;\,a} \right)\], \(B'\left( {a\,;\,0\,;\,a} \right),C'\left( {a\,;\,a\,;\,a} \right),D'\left( {0\,;\,a\,;\,a} \right).\)
Ta thấy \(OC \bot \left( {BB'D'D} \right)\) và \(\overrightarrow {OC} = (a;a;0)\) nên suy ra mặt phẳng \(\left( {BB'D'D} \right)\) có một vectơ pháp tuyến là \[\vec n = \left( {1\,;\,\,1\,;\,\,0} \right).\]+ Đường thẳng \(A'B\) có vectơ chỉ phương là \(\overrightarrow {A'B} = \left( {a\,;\,\,0\,;\,\, - a} \right)\) ta chọn \(\vec u = \left( {1\,;\,\,0\,;\,\, - 1} \right).\)
+ Ta có \(\sin \alpha = \frac{{\left| {\vec n \cdot \vec u} \right|}}{{\left| {\vec n} \right| \cdot \left| {\vec u} \right|}} = \frac{{\left| {1 \cdot 1 + 1 \cdot 0 + 0 \cdot \left( { - 1} \right)} \right|}}{{\sqrt {{1^2} + {1^2} + {0^2}} \cdot \sqrt {{1^2} + {0^2} + {{\left( { - 1} \right)}^2}} }} = \frac{1}{2}.\)
Đáp án: \(\frac{1}{2}.\)
Câu 50:
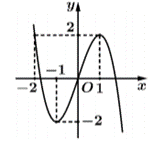
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Có tất cả bao nhiêu giá trị nguyên dương của tham số \(m\) để phương trình \({9^{f\left( x \right)}} + 9m = m \cdot {3^{f\left( x \right)}} + {3^{f\left( x \right) + 2}}\) có đúng 5 nghiệm thực phân biệt?
 Xem đáp án
Xem đáp án
Ta có \({9^{f\left( x \right)}} + 9m = m \cdot {3^{f\left( x \right)}} + {3^{f\left( x \right) + 2}}\)
\( \Leftrightarrow {3^{2f\left( x \right)}} - {3^{f\left( x \right) + 2}} = m\left( {{3^{f\left( x \right)}} - 9} \right)\)\( \Leftrightarrow {3^{f\left( x \right)}}\left( {{3^{f\left( x \right)}} - 9} \right) = m\left( {{3^{f\left( x \right)}} - 9} \right)\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{3^{f\left( x \right)}} = 9}\\{{3^{f\left( x \right)}} = m}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = 2\quad (1)}\\{f\left( x \right) = {{\log }_3}m}\end{array}} \right.} \right.\)
\((1) \Leftrightarrow f\left( x \right) = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = 1}\end{array}} \right.\)
Để phương trình có đúng 5 nghiệm thực phân biệt
\( \Leftrightarrow (2)\) có đúng 3 nghiệm thực khác \( - 2\,;\,\,1\)
\( \Leftrightarrow - 2 < {\log _3}m < 1 \Leftrightarrow \frac{1}{9} < m < 9\).
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6\,;\,\,7\,;\,\,8} \right\}\).
Đáp án: 8.
Câu 51:
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Bốn câu đầu là những cung bậc của sóng và cũng là những cung bậc trong tình yêu của người phụ nữ. Bốn câu sau nhà thơ khẳng định: Tình yêu mãi mãi là khát vọng của tuổi trẻ, nó làm bồi hồi, xao xuyến rung động trái tim của lứa đôi, của con trai con gái, của em và anh. Chọn D.
Câu 52:
 Xem đáp án
Xem đáp án
Câu 53:
 Xem đáp án
Xem đáp án
Hiệu quả nghệ thuật của cách ngắt nhịp, sự luân phiên bằng trắc trong hai câu thơ in đậm là: lời thơ ngắt nhịp 2/3, đồng thời có sự thay đổi tuần hoàn luân phiên các thanh bằng – trắc trong các nhịp ngắt và trong các tiếng cuối của các vế câu thơ (dội – ào – êm – lẽ). Tất cả những điều đó đã khiến cho hai câu thơ như trao đưa giữa những đối cực: dữ dội >< dịu êm, ồn ào >< lặng lẽ. Chọn B.
Câu 54:
 Xem đáp án
Xem đáp án
Những từ ngữ chỉ thời gian mang ý nghĩa tiếp nối, đối lập cùng ý nghĩa khẳng định của từ “vẫn thế” đem đến ý niệm về sự vĩnh hằng về sóng. Sự hòa nhập tinh tế giữa các nét nghĩa ẩn dụ khi tình yêu soi vào sóng để tự nhận thức mình đã đem đến những liên tưởng về tình yêu của em: Giống như những con sóng cứ mãi dào dạt, mãi cồn cào, mãnh liệt trong lòng biển thì những khát vọng tình yêu mãnh liệt trong trái tim em cũng là khát vọng muôn đời của nhân loại. Chọn C.
Câu 55:
 Xem đáp án
Xem đáp án
- Biện pháp tu từ được sử dụng trong hai câu thơ cuối: ẩn dụ (ngực trẻ). Chọn A.
Câu 56:
 Xem đáp án
Xem đáp án
Các thông tin trong đoạn trích cho thấy đoạn trích nói về thức ăn và nước uống của các phi hành gia. Chọn C.
Câu 57:
 Xem đáp án
Xem đáp án
Thông tin nằm ở đoạn 1: Có lẽ bạn đã từng nghe về những loại thức ăn khô thiếu hấp dẫn mà các nhà du hành vũ trụ ăn trong không gian như kem khô, súp đậu sấy khô dạng bột hay thức ăn dạng viên nén. Điều đó có nghĩa là nước bị loại bỏ khỏi những thức ăn đó. Chọn D.
Câu 58:
 Xem đáp án
Xem đáp án
Thông tin nằm ở đoạn 2: Nhiều loại thức ăn bị loại bỏ nước để ngăn ngừa vi khuẩn phát triển, nên cần phải thêm nước vào trước khi ăn. Như vậy việc loại bỏ nước khỏi thức ăn có tác dụng bảo quản thức ăn được lâu hơn. Chọn A.
Câu 59:
 Xem đáp án
Xem đáp án
Thông tin nằm ở đoạn 2: Các phi hành gia được lựa chọn các loại thức ăn yêu thích của mình ở Trái Đất và ăn thử chúng trước đó. Chọn D.
Câu 60:
 Xem đáp án
Xem đáp án
Thông tin nằm ở đoạn 3: Mặc dù, trong mỗi chuyến bay ra ngoài không gian, các phi hành gia mang theo rất nhiều nước nhưng đôi khi vẫn không đủ. Khi đó, họ phải sử dụng nước uống được tái chế từ nước thải của con người. Chọn B.
Câu 61:
 Xem đáp án
Xem đáp án
Các phép liên kết có trong đoạn:
+ Phép nối: Các từ nối: “Bởi thế cho nên”, “Vì những lẽ trên”,...
+ Phép lặp: Lặp lại các từ/ cụm từ: “tự do”, “độc lập”, “dân ta”,....
+ Phép thế: Dùng từ ngữ mang ý nghĩa thay thế “ấy”.
→ Chọn D.
Câu 62:
 Xem đáp án
Xem đáp án
Với câu hỏi này, học sinh tìm để loại những chi tiết có trong văn bản.
- “Pháp chạy, Nhật hàng, vua Bảo Đại thoái vị.” nên loại phương án A.
- “Dân ta đã đánh đổ các xiềng xích thực dân gần một trăm năm nay để gây dựng nên nước Việt Nam độc lập.” nên loại phương án B.
- “Dân ta lại đánh đổ chế độ quân chủ mấy mươi thế kỉ mà lập nên chế độ Dân chủ Cộng hòa.” nên loại phương án D.
→ Chọn C.
Câu 63:
 Xem đáp án
Xem đáp án
Học sinh đọc lại đoạn (5) và xác định được sự lặp đi lặp lại của “một dân tộc đã” + cụm động từ và “dân tộc đó phải được” + tính từ. Và cấu trúc câu từ/ cụm từ “một dân tộc”, “dân tộc”, từ đó xác định đây là 2 dạng của phép điệp ngữ bao gồm điệp từ và điệp cấu trúc. Chọn C.
Câu 64:
 Xem đáp án
Xem đáp án
Học sinh có thể thực hiện câu hỏi này theo 2 cách:
- Cách 1: Học sinh đọc câu hỏi và dựa vào kiến thức từ vựng của mình để xác định nghĩa của từ “thoát li” là tách rời khỏi cái đã có quan hệ gắn bó mật thiết với mình.
- Cách 2: Học sinh đọc câu hỏi, đọc lại đoạn (2) của văn bản, xác định các nội dung “xóa bỏ hết những hiệp ước mới mà Pháp đã kí về nước Việt Nam, xóa bỏ tất cả mọi đặc quyền của Pháp trên đất nước Việt Nam” để suy luận được nước ta tách rời hoàn toàn khỏi sự kiểm soát của Pháp.
→ Chọn A.
Câu 65:
 Xem đáp án
Xem đáp án
Xác định từ khóa “tuyên bố” và các thông tin liên quan: “Nước Việt Nam có quyền hưởng tự do và độc lập, và sự thật đã thành một nước tự do, độc lập. Toàn thể dân tộc Việt Nam quyết đem tất cả tinh thần và lực lượng, tính mạng và của cải để giữ vững quyền tự do, độc lập ấy.”. Chọn B.
Câu 66:
 Xem đáp án
Xem đáp án
Dựa theo hoàn cảnh ra đời của bài thơ và các cụm từ “nhớ, nhớ chơi vơi” đã cho thấy nỗi nhớ là mạch cảm xúc xuyên suốt bài thơ. Chọn A.
Câu 67:
Câu thơ dưới đây sử dụng biện pháp tu từ nào?
Chiều chiều oai linh thác gầm thét
Đêm đêm Mường Hịch cọp trêu người.
 Xem đáp án
Xem đáp án
Nhân hóa (thác gầm thét, cọp trêu người). Chọn B.
Câu 68:
 Xem đáp án
Xem đáp án
Vẻ thơ mộng, trữ tình: hoa về trong đêm hơi, nhà ai Pha Luông mưa xa khơi, Mai Châu mùa em thơm nếp xôi. Vẻ hoang sơ, dữ dội, hiểm trở: sương lấp, dốc lên khúc khuỷu, dốc thăm thẳm, heo hút cồn mây... Chọn D.
Câu 69:
 Xem đáp án
Xem đáp án
Câu 70:
 Xem đáp án
Xem đáp án
Trong cuộc chiến đấu gian khổ, hiện thực là các anh đang đứng ở đỉnh núi cao, với những “dốc thăm thẳm”, nhưng với sự tếu táo, hóm hỉnh đầy chất lính, trong mắt các anh, hiện thực gian khổ trở nên thi vị hóa “súng ngửi trời”. Chọn A.
Câu 71:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Đời Kiều là một tấm gương oan khổ, một câu chuyện thảm thiết về vận mệnh con người trong xã hội cũ.
 Xem đáp án
Xem đáp án
Từ “thảm thiết” có nghĩa hết sức thương tâm, thê thảm, đau xót, thường dùng với các động từ chỉ hành động như “kêu gào”, “khóc lóc”; từ đúng trong câu này là “thảm thương”. Chọn B.
Câu 72:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Chủ nghĩa hiện thực là trào lưu nghệ thuật lấy hiện thực văn học và những vấn đề có thực của con người làm đối tượng sáng tác. Chủ nghĩa hiện thực hướng tới cung cấp cho công chúng nghệ thuật những bức tranh chân thực, sống động, quen thuộc về cuộc sống, về môi trường xã hội xung quanh.
 Xem đáp án
Xem đáp án
Chủ nghĩa hiện thực là trào lưu nghệ thuật lấy hiện thực xã hội và những vấn đề có thực của con người làm đối tượng sáng tác. Chủ nghĩa hiện thực hướng tới cung cấp cho công chúng nghệ thuật những bức tranh chân thực, sống động, quen thuộc về cuộc sống, về môi trường xã hội xung quanh. Chọn B.
Câu 73:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Trong vũ trụ, nếu chỉ riêng loài người biết mình có đời sống tinh thần cao vượt lên trên hết vạn vật; có lí trí phân biệt thị phi thiện ác, quan niệm được tận thiện, tận mĩ để ngày ngày hướng về chỗ chí thiện ấy mà cố sức tiến lên.
 Xem đáp án
Xem đáp án
Chú ý vào từ “nếu” là một từ trong cặp quan hệ từ “nếu – thì” chỉ quan hệ giả thiết – kết quả, nhưng nội dung câu văn chỉ khẳng định sự khác biệt của con người: có đời sống tinh thần, phân biệt thị phi… vậy đây là từ sai, cần lược bỏ để đảm bảo tính mạch lạc trong câu văn. Chọn D.
Câu 74:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Có lẽ chúng ta cần một cái nhìn khác. Rằng chẳng có ước mơ nào tầm thường và chúng ta học không phải để thoát khỏi cái nghề rẻ mạt này, để được làm nghề danh giá kia. Mà học để có thể làm điều mình yêu thích một cách tốt nhất và từ đó mang về cho bản thân thu nhập cao nhất có thể, một cách xứng đáng và tự hào.
 Xem đáp án
Xem đáp án
Nội dung câu văn khẳng định không có công việc, nghề nghiệp nào cao quý hơn, mà con người cần học tập để được làm những điều mình thấy phù hợp.
- Xác định được từ “rẻ mạt” đang dùng sai ngữ nghĩa. Từ này mang nghĩa: không có giá trị, khi dùng sẽ sai với nội dung tổng thể của câu văn.
- Có thể thay từ “rẻ mạt” bằng “thấp hèn” để đảm bảo trái nghĩa với từ “danh giá” phía sau mà không làm thay đổi ý nghĩa câu văn.
→ Chọn B.
Câu 75:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Nếu không trang bị cho mình một vốn hiểu biết về văn học, nghệ thuật thì một tác phẩm hay cũng có giá trị rất ít đối với chúng ta.
 Xem đáp án
Xem đáp án
Từ “rất ít” sử dụng chưa hợp lí. Chọn D.
Câu 76:
 Xem đáp án
Xem đáp án
Từ “bồi hồi” là từ chỉ trạng thái cảm xúc bên trong cơ thể; các từ còn lại trong nhóm (lảo đảo, ngọ nguậy, động đậy) là những hoạt động thể hiện ra bên ngoài, có thể nhìn thấy bằng mắt. Chọn D.
Câu 77:
 Xem đáp án
Xem đáp án
Các từ “háo hức, hăm hở, hăng hái” là từ láy, còn từ “hoa hồng” là từ ghép. Chọn A.
Câu 78:
 Xem đáp án
Xem đáp án
Câu 79:
 Xem đáp án
Xem đáp án
Từ “sáng sủa” là từ láy, các từ còn lại là từ ghép. Chọn C.
Câu 80:
 Xem đáp án
Xem đáp án
Giải nghĩa từ:
- Bẻ: tác động lực từ tay vào vật khiến vật bị gập lại hoặc gãy.
- Nặn, bóp, nắn: tác động lực từ tay vào vật khiến vật bị co, nén lại.
→ Các từ đều miêu tả hành động của tay nhưng từ “bẻ” chỉ hành động gập một vật gì đó lại làm cho gãy. Ba từ còn lại không có nét nghĩa đó. Chọn A.
Câu 81:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Chủ nghĩa trong văn học trung đại rất phong phú, đa dạng, biểu hiện ở lòng thương người; lên án, tố cáo những thế lực tàn bạo chà đạp lên con người; khẳng định, đề cao các mặt phẩm chất, tài năng, những khát vọng chân chính và những quan hệ đạo đức đạo lí tốt đẹp giữa người với người.
 Xem đáp án
Xem đáp án
- Chủ nghĩa nhân đạo thường thể hiện tình yêu thương con người, sự đồng cảm; lên án, tố cáo những thế lực tàn bạo chà đạp lên con người; khẳng định, đề cao các mặt phẩm chất, tài năng, những khát vọng chân chính và những quan hệ đạo đức đạo lí tốt đẹp giữa người với người.
- Chủ nghĩa anh hùng là sự hoàn thành những hành vi xuất sắc có ý nghĩa xã hội tích cực, đòi hỏi sự căng thẳng tột độ của mọi năng lực tinh thần và thể chất, sự dũng cảm, bất khuất, sự sẵn sàng hi sinh của người anh hùng. Hành động anh hùng có tính đạo đức cao, người anh hùng ý thức sâu sắc về việc mình làm là vì điều thiện, vì lợi ích của nhân dân, của dân tộc.
- Chủ nghĩa lãng mạn là sự phản ứng chống lại xã hội đương thời, con người muốn thoát li thực tế tìm đến một thế giới khác giúp con người quên đi cuộc sống mà họ cảm thấy chán ghét, vẽ ra một cuộc sống làm thỏa mãn “cái tôi” bị tổn thương của con người, nên thế giới trong chủ nghĩa lãng mạn là thế giới mộng tưởng.
- Chủ nghĩa hiện sinh làm giảm khả năng lí trí của con người. Thể hiện sự thất vọng khi đi tìm ý nghĩa của cá nhân và ý nghĩa của cộng đồng trong mối tương quan vị trí hợp lí của cá nhân đó, và trật tự của vũ trụ.
→ Chọn C.
Câu 82:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Thói quen đi tìm cái xưa trong cái nay _______ Nguyễn Tuân luôn luôn quan tâm đến chiều thời gian, chiều lịch sử của các sự kiện, các hiện tượng _______ ông quan sát, mô tả.
 Xem đáp án
Xem đáp án
Thói quen đi tìm cái xưa trong cái nay khiến Nguyễn Tuân luôn luôn quan tâm đến chiều thời gian, chiều lịch sử của các sự kiện, các hiện tượng mà ông quan sát, mô tả. Chọn A.
Câu 83:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Bài thơ “Nhàn” (Nguyễn Bỉnh Khiêm) là lời tâm sự , sâu sắc, khẳng định quan niệm sống nhàn là hoà hợp với tự nhiên, giữ cốt cách thanh cao, vượt lên trên danh lợi.
 Xem đáp án
Xem đáp án
Bài thơ “Nhàn” (Nguyễn Bỉnh Khiêm) là lời tâm sự thâm trầm, sâu sắc, khẳng định quan niệm sống nhàn là hoà hợp với tự nhiên, giữ cốt cách thanh cao, vượt lên trên danh lợi. Chọn D.
Câu 84:
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Chế Lan Viên là một trong số những nhà thơ tiêu biểu của phong trào thơ Mới. Trước cách mạng, thơ ông thể hiện một nỗi cô đơn, một ______ bế tắc, tìm đến những “tinh cầu giá lạnh”.
 Xem đáp án
Xem đáp án
Chế Lan Viên là một trong số những nhà thơ tiêu biểu của phong trào thơ Mới. Trước cách mạng, thơ ông thể hiện một nỗi cô đơn, một tâm trạng bế tắc, tìm đến những “tinh cầu giá lạnh”. Chọn C.
Câu 85:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Bình Ngô đại cáo đã tố cáo tội ác kẻ thù xâm lược, ca ngợi cuộc khởi nghĩa Lam Sơn và được coi là bản tuyên ngôn độc lập, một áng của dân tộc ta.
 Xem đáp án
Xem đáp án
“thiên cổ hùng văn” nghĩa là áng văn hùng tráng được lưu truyền đến cả nghìn đời. Chọn B.
Câu 86:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Sớm hôm sau, lính tỉnh dẫn đến cửa ngục thất sáu tên tù mà công văn chiều hôm qua đã báo trước cho ngục quan biết rõ tên tuổi, làng xóm và tội hình. Sáu phạm nhân mang chung một chiếc gông dài tám thước. Cái thang dài ấy đặt ngang trên sáu bộ vai gầy. Cái thang gỗ lim nặng, đóng khung lấy sáu cái cổ phiến loạn, nếu đem bắc lên mỏ cân, có thể nặng đến bảy, tám tạ. Thật là một cái gông xứng đáng với tội án sáu người tử tù. Gỗ thân gông đã cũ và mồ hôi cổ, mồ hôi tay kẻ phải đeo nó đã phủ lên một nước quang dầu bóng loáng. Những đoạn gông đã bóng thì loáng như có người đánh lá chuối khô. Những đoạn không bóng thì lại xỉn lại những chất ghét đen sánh. Trong khi chờ đợi cửa ngục mở rộng, Huấn Cao, đứng đầu gông, quay cổ lại bảo mấy bạn đồng chí:
– Rệp cắn tôi, đỏ cả cổ lên rồi. Phải dỗ gông đi.
Sáu người đều qùy cả xuống đất, hai tay ôm lấy thành gông đầu cúi cả về phía trước. Một tên lính áp giải đùa một câu:
– Các người chả phải tập nữa. Mai mốt chi đây sẽ có người sành sỏi dẫn các người ra làm trò ở pháp trường. Bấy giờ tha hồ mà tập. Đứng dậy không ông lại phết cho mấy hèo bây giờ.
Huấn Cao, lạnh lùng, chúc mũi gông nặng, khom mình thúc mạnh đầu thang gông xuống thềm đá tảng đánh thuỳnh một cái. Then ngang chiếc gông bị giật mạnh, đập vào cổ năm người sau, làm họ nhăn mặt. Một trận mưa rệp đã làm nền đá xanh nhạt lấm tấm những điểm nâu đen.
(Chữ người tử tù – Nguyễn Tuân)
Đoạn trích trên thể hiện nét tính cách gì ở nhân vật Huấn Cao?
 Xem đáp án
Xem đáp án
Đoạn trích thể hiện khí phách hiên ngang của Huấn Cao bởi ông không sợ ngục tù, không sợ phải đối mặt với cái chết. Điều đó được thể hiện qua hành động “dỗ gông”, “chúc mũi gông nặng, khom mình thúc mạnh đầu thang gông xuống thềm đá đánh thuỳnh một cái....”. Chọn A.
Câu 87:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Xác hàng thịt: (bắt đầu) Vô ích, cái linh hồn mờ nhạt của ông Trương Ba khốn khổ kia ơi, ông không tách ra khỏi tôi được đâu, dù tôi chỉ là thân xác...
Hồn Trương Ba: A, mày cũng biết nói kia à? Vô lí, mày không thể biết nói! Mày không có tiếng nói, mà chỉ là xác thịt âm u đui mù...
Xác hàng thịt: Có đấy! Xác thịt có tiếng nói đấy! Ông đã biết tiếng nói của tôi rồi, đã luôn luôn bị tiếng nói ấy sai khiến. Chính vì âm u, đui mù mà tôi có sức mạnh ghê gớm, lắm khi át cả cái linh hồn cao khiết của ông đấy!
Hồn Trương Ba: Nói láo! Mày chỉ là cái vỏ bên ngoài, không có ý nghĩa gì hết, không có tư tưởng, không có cảm xúc!
(Hồn Trương Ba, da hàng thịt – Lưu Quang Vũ)
Đoạn trích thể hiện thái độ gì của nhân vật “hồn Trương Ba” với “xác hàng thịt”?
 Xem đáp án
Xem đáp án
Đoạn trích là cuộc đối thoại giữa “hồn Trương Ba” với “xác hàng thịt” trong đó hồn thể hiện thái độ tức giận, khinh bỉ với xác hàng thịt. Ông uất ức, tức giận vì phải chung sống với xác thô lỗ, tầm thường, dung tục, thể hiện thái độ khinh bỉ đối với xác hàng thịt: “Mày không có tiếng nói, mà chỉ là xác thịt âm u đui mù”. Chọn A.
Câu 88:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tiếng ai tha thiết bên cồn
Bâng khuâng trong dạ, bồn chồn bước đi
Áo chàm đưa buổi phân li
Cầm tay nhau biết nói gì hôm nay...
(Việt Bắc – Tố Hữu)
Âm hưởng chủ đạo của đoạn trích trên là gì?
 Xem đáp án
Xem đáp án
Đoạn thơ là buổi chia tay bịn rịn, lưu luyến giữa người dân Việt Bắc và chiến sĩ cách mạng, vì vậy âm hưởng chủ đạo của đoạn trích là nhớ nhung, lưu luyến. Chọn A.
Câu 89:
Đọc đoạn trích sau và trả lời câu hỏi:
Tỉnh dậy hắn thấy già mà vẫn còn cô độc. Buồn thay cho đời! Có lí nào như thế được? Hắn đã già rồi hay sao? Ngoài bốn mươi tuổi đầu... Dẫu sao, đó không phải tuổi mà người ta mới bắt đầu sửa soạn. Hắn đã tới cái dốc bên kia của đời. Ở những người như hắn, chịu đựng biết bao nhiêu là chất độc, đầy đọa cực nhọc mà chưa bao giờ ốm, một trận ốm có thể gọi là dấu hiệu báo rằng cơ thể đã hư hỏng nhiều. Nó là một cơn mưa gió cuối thu cho biết trời gió rét, nay mùa đông đã đến. Chí Phèo hình như đã trông thấy trước tuổi già của hắn, đói rét và ốm đau, và cô độc, cái này còn đáng sợ hơn đói rét và ốm đau.
(Chí Phèo – Nam Cao)
Xác định biện pháp tu từ được sử dụng trong câu in đậm.
 Xem đáp án
Xem đáp án
Câu 90:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Một người đàn bà đã xóa hết tên, tuổi trên mọi văn bản của mình
Rồi đến tìm tôi
Nàng rung quả chuông trong ngực tôi
Nàng thắp ngọn nến trong mắt tôi
Nàng mở cánh cửa trong tai tôi
Nàng thay chân tôi bằng chân ngựa hoang
Nàng thay tay tôi bằng cánh đại bàng.
(Nguyễn Quang Thiều, Đau gần lúc sáng, theo Nhật kí người xem đồng hồ,
NXB Hội Nhà văn, 2023)
Phong cách ngôn ngữ của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Phong cách ngôn ngữ của đoạn trích là nghệ thuật. Chọn A.
Câu 91:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Bạn bước vào rạp chiếu bóng cùng với vài người bạn […]. Có điều gì đó rất thần bí đang diễn ra. Bạn có ấn tượng tưởng như mình đang thấy một hình ảnh chuyển động, song nó chỉ là một ảo ảnh. Hình ảnh chuyển động liên tục mà bạn trông thấy đó bao gồm hàng ngàn những ảnh tĩnh có tên gọi là khuôn hình, giữa chúng khác nhau rất ít, được chiếu lên màn ảnh trong một chuỗi tiếp nối rất nhanh. Mắt chúng ta bỏ qua những khoảng cách mà chỉ nhìn thấy những ánh sáng liên tục từ một chuỗi những hình ảnh tĩnh […]. Vậy cái gì đã khiến một bộ phim chuyển động? Chẳng ai đưa ra được câu trả lời đầy đủ. Nhiều người suy đoán rằng sở dĩ có hiệu quả đó là do “sự đeo bám dai dẳng của thị giác” theo chiều hướng một hình ảnh lưu lại ngắn ngủi trên con ngươi mắt. Tuy nhiên, nếu đó đúng là nguyên nhân chính, thì chúng ta sẽ thấy nhòe nhoẹt rối mắt những tấm ảnh bất động, lộ sáng nhiều lần chứ không phải là hành động trôi chảy. Hiện thời các nhà nghiên cứu tin rằng đã có hai quá trình tâm lí tham dự vào chuyển động của phim ảnh: Sự hội tụ ánh sáng cực hạn và sự chuyển động rõ rệt.
(David Borwell & Kristin Thompson, Nghệ thuật điện ảnh, NXB Giáo dục, 2008)
Phong cách ngôn ngữ của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Đoạn trích sử dụng phong cách ngôn ngữ khoa học nhằm giải thích sự chuyển động của phim ảnh. Chọn B.
Câu 92:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Từ đây, như đã tìm đúng đường về, sông Hương vui tươi hẳn lên giữa những biền bãi xanh biếc của vùng ngoại ô Kim Long, kéo một nét thẳng thực yên tâm theo hướng tây nam - đông bắc, phía đó, nơi cuối đường, nó đã nhìn thấy chiếc cầu trắng của thành phố in ngần trên nền trời, nhỏ nhắn như những vành trăng non. Giáp mặt thành phố ở Cồn Giã Viên, sông Hương uốn một cánh cung rất nhẹ sang đến Cồn Hến; đường cong ấy làm cho dòng sông mềm hẳn đi, như một tiếng “vâng” không nói ra của tình yêu. Và như vậy, giống như sông Xen (Seine) của Pa-ri (Paris), sông Đa-nuýp (Danube) của Bu-đa-pét (Budapest); sông Hương nằm ngay giữa lòng thành phố yêu quý của mình; Huế trong tổng thể vẫn giữ nguyên dạng một đô thị cổ, trải dọc hai bờ sông. Đầu và cuối ngõ thành phố, những nhánh sông đào mang nước sông Hương toả đi khắp phố thị, với những cây đa, cây cừa cổ thụ toả vầng lá u sầm xuống những xóm thuyền xúm xít; từ những nơi ấy, vẫn lập loè trong đêm sương những ánh lửa thuyền chài của một linh hồn mô tê xưa cũ mà không một thành phố hiện đại nào còn nhìn thấy được.
(Ai đã đặt tên cho dòng sông? – Hoàng Phủ Ngọc Tường)
Đoạn trích trên miêu tả hình ảnh sông Hương ở không gian nào?
 Xem đáp án
Xem đáp án
Đoạn trích miêu tả hình ảnh sông Hương trong lòng thành phố Huế. Căn cứ vào các chi tiết được nhắc tới trong đoạn trích: nhìn thấy chiếc cầu trắng của thành phố, nhắc đến các địa danh trong thành phố Huế như Cồn Giã Viên, Cồn Hến, đặc biệt chú ý câu văn khẳng định sông Hương nằm ngay giữa lòng thành phố yêu quý của mình. Chọn C.
Câu 93:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trước cái xa xanh thanh khiết không lời
Cái hào hiệp ngang tàng của gió
Cái kiên nhẫn nghìn đời sóng vỗ
Cái nghiêm trang của đá đứng chen trời
Cái giản đơn sâu sắc như đời
Cái trời kia biển mãi gọi người đi
Bao khát vọng nửa chừng tan giữa sóng
Vầng trán mặt giọt mồ hôi cay đắng
Bao kiếp vùi trong đáy lạnh mù tăm
Nhưng muôn đời vẫn những cánh buồm căng
Bay trên biển như bồ câu trên đất
Biển dư sức và người không biết mệt
Mũi thuyền lao mặt sóng lại cày bừa
Những chân trời ta vẫn mãi tìm đi
(Trước biển, Vũ Quần Phương, Thơ Việt Nam 1945 – 1985, NXB Văn học, 1985, tr. 391)
Mối quan hệ giữa “biển” và “người” trong đoạn thơ là mối quan hệ như thế nào?
 Xem đáp án
Xem đáp án
Mối quan hệ giữa “biển” và “người” là mối quan hệ gắn bó khăng khít không thể tách rời: “…muôn đời vẫn những cánh buồm căng/ Bay trên biển như bồ câu trên đất/ Biển dư sức và người không biết mệt”. Chọn C.
Câu 94:
Đọc đoạn trích sau và trả lời câu hỏi:
Bà lão khẽ thở dài đứng lên, đăm đăm nhìn người đàn bà. Thị cúi mặt xuống, tay vân vê tà áo đã rách bợt. Bà lão nhìn thị và bà nghĩ: Người ta có gặp bước khó khăn, đói khổ này, người ta mới lấy đến con mình. Mà con mình mới có vợ được... Thôi thì bổn phận bà là mẹ, bà đã chẳng lo lắng được cho con... May ra mà qua khỏi được cái tao đoạn này thì thằng con bà cũng có vợ, nó yên bề nó, chẳng may ra ông giời bắt chết cũng phải chịu chứ biết thế nào mà lo cho hết được?
(Vợ nhặt – Kim Lân)
Đoạn trích trên thể hiện phẩm chất gì của bà cụ Tứ?
 Xem đáp án
Xem đáp án
Đoạn trích thể hiện phẩm chất tốt đẹp của bà cụ Tứ. Đó là một người mẹ yêu thương con. Bà thừa hiểu mục đích thị đồng ý lấy Tràng là để kiếm miếng ăn chứ không hề xuất phát từ tình yêu. Hơn nữa trong hoàn cảnh nạn đói bà hoàn toàn có thể không chấp nhận thị. Thế nhưng bà vẫn bằng lòng bởi bà nghĩ nhờ có thế mà con bà mới có vợ và bà cảm thấy vui vì điều này. Chọn A.
Câu 95:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tiếng Việt có những đặc sắc của một thứ tiếng đẹp, một thứ tiếng hay. Nói thế có nghĩa là nói rằng: tiếng Việt là một thứ tiếng hài hòa về mặt âm hưởng, thanh điệu mà cũng rất tế nhị, uyển chuyển trong cách đặt câu. Nói thế cũng có nghĩa là nói rằng: tiếng Việt có đầy đủ khả năng để diễn đạt tình cảm, tư tưởng của người Việt Nam và thỏa mãn cho yêu cầu của đời sống văn hóa nước nhà qua các thời kì lịch sử.
(Theo Đặng Thai Mai)
Xác định câu văn chứa luận điểm trong đoạn văn.
 Xem đáp án
Xem đáp án
“Tiếng Việt có những đặc sắc của một thứ tiếng đẹp, một thứ tiếng hay.” là câu văn mang luận điểm, khái quát nội dung chính mà tác giả sẽ triển khai sau đó. Chọn A.
Câu 96:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Nếu Tổ quốc neo mình đầu sóng cả
Những chàng trai ra đảo đã quên mình
Một sắc chỉ về Hoàng Sa thuở trước
Còn truyền đời con cháu mãi đinh ninh
Nếu Tổ quốc nhìn từ bao mất mát
Máu xương kia dằng dặc suốt ngàn đời
Hồn dân tộc ngàn năm không chịu khuất
Dáng con tàu vẫn hướng mãi ra khơi.
(Nguyễn Việt Chiến, Tổ quốc nhìn từ biển, NXB Phụ nữ, 2015)
Nhân vật trữ tình đã gửi gắm cảm xúc, tâm tư gì vào đoạn thơ?
 Xem đáp án
Xem đáp án
Học sinh đọc ngữ liệu, căn cứ vào các hình ảnh “chàng trai ra đảo đã quên mình, máu xương kia dằng dặc suốt ngàn đời, hồn dân tộc ngàn năm không chịu khuất” để thấy những suy ngẫm, chiêm nghiệm của tác giả, đồng thời cùng với đó là sự trân trọng, tự hào đối với lịch sử bảo vệ biển đảo, bảo vệ Tổ quốc. Học sinh căn cứ tiếp vào câu “Dáng con tàu vẫn hướng mãi ra khơi” để thấy sự tiến về phía trước của thế hệ tương lai, thể hiện trách nhiệm của thế hệ trẻ đối với công cuộc bảo vệ Tổ quốc. Chọn B.
Câu 97:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tiếng trống thu không trên cái chợ của huyện nhỏ; từng tiếng một vang xa để gọi buổi chiều. Phương tây đỏ rực như lửa cháy và những đám mây ánh hồng như hòn than sắp tàn. Dãy tre làng trước mặt đen lại và cắt hình rõ rệt trên nền trời.
Chiều, chiều rồi. Một chiều êm ả như ru, văng vẳng tiếng ếch nhái kêu ran ngoài đồng ruộng theo gió nhẹ đưa vào. Trong cửa hàng hơi tối, muỗi đã bắt đầu vo ve. Liên ngồi yên lặng bên mấy quả thuốc sơn đen; đôi mắt chị bóng tối ngập đầy dần và cái buồn của buổi chiều quê thấm thía vào tâm hồn ngây thơ của chị: Liên không hiểu sao, nhưng chị thấy lòng buồn man mác trước cái giờ khắc của ngày tàn.
(Hai đứa trẻ – Thạch Lam)
Màu sắc nào KHÔNG xuất hiện trong khung cảnh ở đoạn trích trên?
 Xem đáp án
Xem đáp án
Màu sắc không xuất hiện trong khung cảnh ở đoạn trích là: Vệt sáng của những con đom đóm bay là là trên mặt đất hay len vào những cành cây. Chọn C.
Câu 98:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Chưa chữ viết đã vẹn tròn tiếng nói
Vầng trăng cao đêm cá lặn sao mờ
Ôi tiếng Việt như đất cày, như lụa
Óng tre ngà và mềm mại như tơ
Tiếng tha thiết nói thường nghe như hát
Kể mọi điều bằng ríu rít âm thanh
Như gió nước không thể nào nắm bắt
Dấu huyền trầm, dấu ngã chênh vênh.
(trích “Tiếng Việt”- Lưu Quang Vũ)
Nội dung chính của đoạn trích là gì?
 Xem đáp án
Xem đáp án
Đoạn trích thể hiện tình cảm yêu mến, trân trọng và tự hào của tác giả dành cho vẻ đẹp và sự giàu có, phong phú của tiếng Việt. Chọn B.
Câu 99:
Đọc đoạn trích sau và trả lời câu hỏi:
Mỗi chiếc lá rụng là một cái biểu hiện cho một cảnh biệt ly. Vậy thì sự biệt ly không chỉ có một nghĩa buồn rầu, khổ sở. Sao ta không ngắm sự biệt ly theo tâm hồn một chiếc lá nhẹ nhàng rơi?
(Theo Khái Hưng)
Câu nghi vấn trong đoạn trên dùng để làm gì?
 Xem đáp án
Xem đáp án
Câu nghi vấn ngoài chức năng để hỏi còn được sử dụng với một số chức năng khác như để khẳng định, phủ định, cầu khiến, đe dọa, bộc lộ cảm xúc,… Câu nghi vấn trong đoạn văn được dùng để cầu khiến. Chọn B.
Câu 100:
Đọc đoạn trích sau đây và trả lời câu hỏi:
…Còn xa lắm mới đến cái thác dưới. Nhưng đã thấy tiếng nước réo gần mãi lại, réo to mãi lên. Tiếng nước thác nghe như là oán trách gì, rồi lại như là van xin, rồi lại như là khiêu khích, giọng gằn mà chế nhạo. Thế rồi nó rống lên như tiếng một ngàn con trâu mộng đang lồng lộn giữa rừng vầu, rừng tre nứa nổ lửa, đang phá tuông rừng lửa, rừng lửa cùng gầm thét với đàn trâu da cháy bùng bùng. Tới cái thác rồi. Ngoặt khúc sông lượn, thấy sóng bọt đã trắng xoá cả chân trời đá.
Đá ở đây từ ngàn năm vẫn mai phục hết trong lòng sông, hình như mỗi lần có chiếc thuyền nào xuất hiện ở quãng ầm ầm mà quạnh hiu này, mỗi lần có chiếc nào nhô vào đường ngoặt sông là một số hòn bèn nhổm cả dậy để vồ lấy thuyền. Mặt hòn đá nào trông cũng ngỗ ngược, hòn nào cũng nhăn nhúm méo mó hơn cả cái mặt nước chỗ này.
(Người lái đò Sông Đà – Nguyễn Tuân)
Đoạn văn bản trên Nguyễn Tuân đã sử dụng tổng hợp tri thức của những ngành nào?
 Xem đáp án
Xem đáp án
Trong đoạn trích, Nguyễn Tuân đã sử dụng tổng hợp tri thức của nhiều ngành. Cụ thể:
- Âm nhạc: tả âm thanh tiếng thác: nước réo gần mãi lại, réo to mãi lên…
- Hội hoạ: vẽ bộ mặt của Đá: nhăn nhúm méo mó
- Quân sự: mai phục.
Hiệu quả nghệ thuật của việc sử dụng đó là: thể hiện phong cách tài hoa, uyên bác của Nguyễn Tuân khi tả dòng sông Đà. Con sông được nhìn ở nhiều góc độ, trở nên sống động, mạnh mẽ, ấn tượng, thể hiện tình yêu thiên nhiên sâu đậm của nhà văn. Chọn A.
Câu 101:
PHẦN 3: KHOA HỌC
Lĩnh vực: Khoa học tự nhiên và xã hội (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Dưới tác động từ hai cuộc khai thác thuộc địa của thực dân Pháp, công nhân từng bước lớn mạnh và trở thành giai cấp lãnh đạo cách mạng giải phóng dân tộc Việt Nam. Năm 1930, Đảng Cộng sản Việt Nam được thành lập, đưa giai cấp công nhân thành giai cấp lãnh đạo cách mạng. Chọn C.
Câu 102:
 Xem đáp án
Xem đáp án
Để đưa nước Mỹ thoát khỏi khủng hoảng, Tổng thống Mỹ Ru-dơ-ven (Roosevelt) đã thực hiện Chính sách mới. Chọn D.
Câu 103:
 Xem đáp án
Xem đáp án
Phân tích các đáp án, ta thấy:
A loại vì nhiệm vụ được đề ra trong Cương lĩnh chính trị (đầu năm 1930) và Luận cương chính trị (10/1930) là khác nhau. Cụ thể:
- Nhiệm vụ cách mạng được nêu trong Cương lĩnh chính trị là tiến hành cách mạng tư sản dân quyền và thổ địa cách mạng để đi tới xã hội cộng sản, trong đó, đề cao vấn đề giải phóng dân tộc.
- Nhiệm vụ của Luận cương chính trị lại nêu nhiệm vụ của cách mạng là đánh đổ phong kiến và đánh đổ đế quốc, trong đó, vấn đề giai cấp được nêu cao hơn (đây là hạn chế của Luận cương).
B, C loại vì lực lượng cách mạng/động lực cách mạng được xác định trong Cương lĩnh là công nhân, nông dân, trí thức, tiểu tư sản (là các lực lượng nòng cốt) còn phú nông, trung tiểu địa chủ thì cần phải lợi dung hoặc trung lập. Luận cương chính trị chỉ xác định lực lượng/động lực cách mạng là công nhân và nông dân (hạn chế).
Chọn D.
Câu 104:
 Xem đáp án
Xem đáp án
Kế hoạch Đờ Lát đơ Tatxinhi ra đời là kết quả của sự cấu kết giữa Pháp và Mĩ trong việc đẩy mạnh cuộc chiến ở Đông Dương. Chọn A.
Câu 105:
 Xem đáp án
Xem đáp án
Mua bằng phát minh sáng chế của nước ngoài là điểm khác biệt trong phát triển khoa học-kĩ thuật của Nhật Bản so với các nước tư bản khác. Chọn C.
Câu 106:
 Xem đáp án
Xem đáp án
Nội dung nào sau đây không phải là nhiệm vụ chiến lược của cách mạng Việt Nam thời kỳ 1954-1975 là cả nước tiếp tục cuộc cách mạng dân tộc dân chủ nhân dân vì đến năm 1954 thì miền Bắc đã hoàn thành cách mạng dân tộc dân chủ nhân dân. Chọn D.
Câu 107:
 Xem đáp án
Xem đáp án
Những năm đầu sau Cách mạng tháng Tám (1945), nước Việt Nam Dân chủ Cộng hòa đang ở trong tình thế bị bao vây, cô lập vì chưa có nước nào công nhận nền độc lập, thiết lập quan hệ ngoại giao. Phải đến năm 1950 thì Trung Quốc là quốc gia đầu tiên thiết lập quan hệ ngoại giao với Việt Nam Dân chủ Cộng hòa. Chọn B.
Câu 108:
 Xem đáp án
Xem đáp án
Trong cuộc kháng chiến toàn quốc chống thực dân Pháp của nhân dân Việt Nam (1946 - 1954) chiến thắng Việt Bắc thu - đông năm 1947 đã làm phá sản "kế hoạch đánh nhanh thắng nhanh". Chọn C.
Câu 109:
 Xem đáp án
Xem đáp án
Phương án C sai vì phát xit Nhật đảo chính lật đổ Pháp ở Đông Dương từ tháng 3 năm 1945. Chọn C.
Câu 110:
 Xem đáp án
Xem đáp án
Để có được thắng lợi của Cách mạng tháng Tám năm 1945 ở Việt Nam thì quân và dân ta đã có quá trình chuẩn bị lâu dài trong suốt 15 năm với 3 cuộc tập dượt; cùng với đó là nghệ thuật chớp thời cơ "ngàn năm có một" để làm nên một thắng lợi nhanh chóng, it đổ máu.
Chọn C.
Câu 111:
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
A. Nhiều quốc gia thuộc vào nhóm nước phát triển. → đây không phải thành tựu.
B. Các quốc gia đều có trình độ phát triển giống nhau. → sai, không giống nhau.
C. Tình trạng đói nghèo của người dân đã được xóa bỏ. → sai, chưa được xóa bỏ.
D. Tốc độ tăng GDP của một số quốc gia đã khá cao. → đúng. Chọn D.
Câu 112:
 Xem đáp án
Xem đáp án
Miền Tây Trung Quốc là nơi có nhiều hoang mạc và bán hoang mạc rộng lớn. Chọn A.
Câu 113:
 Xem đáp án
Xem đáp án
Miền Bắc không có một mùa khô sâu sắc kéo dài. Chọn C.
Câu 114:
 Xem đáp án
Xem đáp án
Vai trò quan trọng nhất của rừng đầu nguồn là là điều hòa nguồn nước sông.
A. tạo sự đa dạng sinh học. → đây là vai trò của rừng đặc dụng.
B. điều hoà nguồn nước của các sông. → đúng. Chọn B.
C. điều hoà khí hậu, chắn gió bão. → → đây là vai trò của rừng đặc dụng.
D. cung cấp gỗ và lâm sản quý. → không phải vai trò của rừng đầu nguồn.
Câu 115:
 Xem đáp án
Xem đáp án
Dãy Hoàng Liên Sơn nằm gần thung lũng sông Hồng. Chọn A.
Câu 116:
Cho biểu đồ:
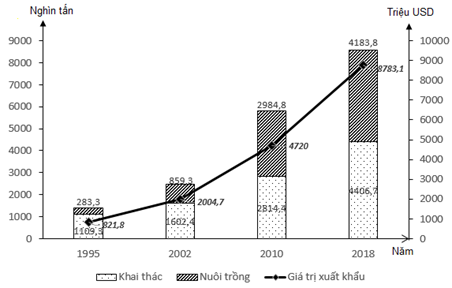
SẢN LƯỢNG THỦY SẢN VÀ GIÁ TRỊ THỦY SẢN XUẤT KHẨU
Từ biểu đồ trên, hãy cho biết đáp án nào sau đây là nhận xét không đúng?
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
- Chọn A. Sản lượng thủy sản khai thác tăng 3297,4 nghìn tấn → nhận xét A sai
- Chọn B: sản lượng thủy sản nuôi trồng tăng 14,8 lần, thủy sản khai thác tăng gần 4 lần → nuôi trồng tăng nhanh hơn khai thác → B đúng
- Chọn C: Nuôi trồng tăng 3900,5 nghìn tấn; khai thác tăng 3294,7 nghìn tấn → nuôi trồng tăng nhiều hơn → C đúng
- Chọn D: giá trị xuất khẩu tăng 10,7 lần; sản lượng thủy sản tăng 6,2 lần → giá trị xuất khẩu tăng nhanh hơn sản lượng thủy sản → D đúng
Câu 117:
 Xem đáp án
Xem đáp án
Đường dây 500 KV được xây dựng nhằm mục đích khắc phục tình trạng mất cân đối về điện năng của các vùng lãnh thổ, vì điện không lưu trữ được nên cần có đường dây truyền tải điện. Chọn D.
Câu 118:
 Xem đáp án
Xem đáp án
Sử dụng than trong sản xuất nhiệt điện ở nước ta gây ra nhiều vấn đề môi trường, nhưng chủ yếu nhất là ô nhiễm không khí. Chọn B.
Câu 119:
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
A. Đông dân, lao động dồi dào, kinh tế chậm chuyển dịch. → đúng, đủ. Chọn A.
B. Đông dân, lao động dồi dào và sự phân bố không đều. → phân bố không đều không quan trọng bằng kinh tế chậm chuyển dịch.
C. Lao động dồi dào và lao động có nhiều kinh nghiệm. → không gây ra thiếu việc làm.
D. Lao động dồi dào, tập trung chủ yếu ở ngành công nghiệp. → tập trung ở ngành công nghiệp không tạo ra thiếu việc làm.
Câu 120:
 Xem đáp án
Xem đáp án
Việc khai thác lãnh thổ theo chiều sâu trong công nghiệp ở Đông Nam Bộ đặt ra vấn đề cấp bách là tăng cường cơ sở năng lượng. Vấn đề này phải đi trước một bước để có thể phát triển các ngành sau. Chọn B.
Câu 121:
 Xem đáp án
Xem đáp án
Nguyên nhân gây ra điện trở của kim loại là sự va chạm của các electron tự do với nhau trong quá trình chuyển động nhiệt hỗn loạn. Chọn A.
Câu 122:
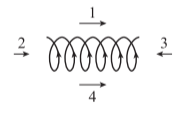
 Xem đáp án
Xem đáp án
Quy tắc nắm bàn tay phải xác định chiều của từ trường tạo bởi dòng điện trong ống dây. Chọn B.
Câu 123:
 Xem đáp án
Xem đáp án
Ta có:
\(\sin i = \frac{{{n_2}}}{{{n_1}}}\sin {r_{12}} = \frac{{{n_3}}}{{{n_1}}}\sin {r_{13}} \to \frac{{{n_3}}}{{{n_2}}} = \frac{{\sin {r_{12}}}}{{\sin {r_{13}}}} = \frac{{\sin 30^\circ }}{{\sin 45^\circ }} = \frac{{\sqrt 2 }}{2} = \sin {i_{gh}} \to {i_{gh}} = 45^\circ \approx 46^\circ \).
Chọn C.
Câu 124:

 Xem đáp án
Xem đáp án
Sự phát quang này kéo dài hàng giờ, rất thuận tiện cho việc tìm chỗ bật đèn trong đêm là hiện tượng lân quang. Chọn C.
Câu 125:
 Xem đáp án
Xem đáp án
Tần số của ngoại lực tăng dần từ \(0,5\;{\rm{Hz}}\) đến \(2,0\;{\rm{Hz}}\) thì biên độ của con lắc không thay đổi. Chọn B.
Câu 126:
Sự phụ thuộc của cảm kháng ZL của cuộn dây thuần cảm có độ tự cảm L không đổi vào tần số f của dòng điện xoay chiều hình sin chạy qua cuộn dây được diễn tả bởi đồ thị ở hình nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Ta có \({Z_L} = 2\pi fL \to \) đồ thị biểu diễn là hàm tuyến tính. Chọn A.
Câu 127:
 Xem đáp án
Xem đáp án
Số hạt nhân còn lại sau t = 1 năm là \(N = {N_0} \cdot {2^{ - \frac{t}{T}}} = \frac{{{N_0}}}{3} \Rightarrow {2^{ - \frac{t}{T}}} = \frac{1}{3}\)
Số hạt nhân còn lại sau t’ = 1 năm tiếp theo là
Chọn C.
Câu 128:
 Xem đáp án
Xem đáp án
Biên độ của điểm M và N là: \[\left\{ {\begin{array}{*{20}{c}}{{A_M} = {A_{bung}}.\left| {\sin \frac{{2\pi {x_M}}}{\lambda }} \right| = {A_{bung}}.\left| {\sin \frac{{2\pi .16}}{{24}}} \right| = {A_{bung}}.\frac{{\sqrt 3 }}{2}}\\{{A_N} = {A_{bung}}.\left| {\sin \frac{{2\pi {x_N}}}{\lambda }} \right| = {A_{bung}}.\left| {\sin \frac{{2\pi .27}}{{24}}} \right| = {A_{bung}}.\frac{{\sqrt 2 }}{2}}\end{array}} \right.\]
Tỉ số giữa biên độ dao động của M và N là: \[\frac{{{A_M}}}{{{A_N}}} = \frac{{{A_{bung}}.\frac{{\sqrt 3 }}{2}}}{{{A_{bung}}.\frac{{\sqrt 2 }}{2}}} = \frac{{\sqrt 3 }}{{\sqrt 2 }} = \frac{{\sqrt 6 }}{2}\]
Chọn D.
Câu 129:
Trong các hình sau, hình nào diễn tả đúng mối quan hệ giữa các thành phần trong sóng điện từ?
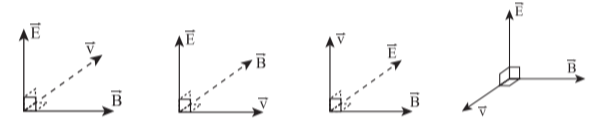
 Xem đáp án
Xem đáp án
Quy tắc bàn tay trái xác định mỗi quan hệ giữa thành phần trong sóng điện từ.
Chọn A.
Câu 130:
Cho đoạn mạch xoay chiều như hình vẽ:
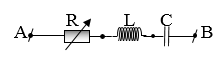
Biết \(L = \frac{1}{\pi }H;C = \frac{{{{10}^{ - 3}}}}{{4\pi }}F\). Đặt vào hai đầu đoạn mạch một hiệu điện thế: \({U_{AB}} = 75\sqrt 2 \cos \left( {100\pi } \right)\left( V \right)\). Công suất trên toàn mạch là \(P = 45\left( {\rm{W}} \right)\). Tính giá trị R (tính theo đơn vị Ω)?
 Xem đáp án
Xem đáp án
\({Z_L} = \omega L = 100\Omega \)
\({Z_C} = \frac{1}{{\omega C}} = 40\Omega \)
\(U = 75V\)
\(P = 45\left( {\rm{W}} \right)\)
Công suất tiêu thụ toàn mạch là: \(P = \frac{{{U^2}R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \frac{{{U^2}R}}{{{R^2} + {{60}^2}}}\)
\( \Leftrightarrow 45 = \frac{{{{75}^2}.R}}{{{R^2} + {{60}^2}}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{R = 45\Omega }\\{R = 80\Omega }\end{array}} \right.\)
Đáp án: 45 hoặc 80.
Câu 131:
 Xem đáp án
Xem đáp án
Bình \[{H_2}S{O_4}\]đặc hấp thụ \[{H_2}O\]⟹ \[{m_{{H_2}O}} = 21,6\left( g \right) \to {n_{{H_2}O}} = \frac{{21,6}}{{18}} = 1,2\left( {mol} \right)\]
Bảo toàn nguyên tố H ⟹ \[{n_H} = 2{n_{{H_2}O}} = 2 \cdot 1,2 = 2,4\left( {mol} \right)\]
Bảo toàn khối lượng ⟹ \[{m_C} = {m_{hh}} - {m_H} = 12 - 2,4 \cdot 1 = 9,6\left( g \right) \to {n_C} = \frac{{9,6}}{{12}} = 0,8\left( {mol} \right)\]
Bảo toàn nguyên tố C ⟹ \[{n_{C{O_2}}} = {n_C} = 0,8\left( {mol} \right) \to {V_{C{O_2}\left( {dktc} \right)}} = 0,8 \cdot 22,4 = 17,92\left( l \right)\].
Tỷ lệ: 12 gam hỗn hợp sinh ra 17,92 lít khí \[C{O_2}.\]
⟹ 100 gam hỗn hợp sinh ra 149,33 lít khí \[C{O_2}.\]
Chọn A.
Câu 132:
 Xem đáp án
Xem đáp án
Phương trình hóa học:
\[{M_2}{O_m}\;{\rm{ }} + \;{\rm{ }}m{H_2}S{O_4}\; \to \;{\rm{ }}{M_2}{\left( {S{O_4}} \right)_m}\;{\rm{ }} + \;{\rm{ }}m{H_2}O\]
Giả sử có 1 mol \[{M_2}{O_m}\] phản ứng thì số gam dung dịch \[{H_2}S{O_4}\;10\% \] là 980m (g)
Khối lượng dung dịch thu được là: (2M + 16m) + 980m = 2M + 996m (g)
Số gam muối là: 2M + 96m (g)
Ta có C% = \(\frac{{2M + 96m}}{{2M + 996m}}.100\% \) = 12,9% ⟹ M = 18,65m
Nghiệm phù hợp là m = 3 và M = 56 (Fe).
Vậy oxide là \[F{e_2}{O_3}.\]
\[F{e_2}{O_3}\; + {\rm{ }}\;3{H_2}S{O_4}\; \to \;{\rm{ }}F{e_2}{\left( {S{O_4}} \right)_3}\;{\rm{ }} + \;{\rm{ }}3{H_2}O\]
\( \Rightarrow {n_{F{e_2}{O_3}}} = \frac{{3,2}}{{160}} = 0,02\,\,mol\)
Vì hiệu suất là 70% nên số mol \[F{e_2}{\left( {S{O_4}} \right)_3}\;\]tham gia kết tinh là: 0,02.70% = 0,014 mol
Nhận thấy số gam \[F{e_2}{\left( {S{O_4}} \right)_3}\;\]= 0,014.400 = 5,6 gam < 7,868 gam nên tinh thể là muối ngậm nước.
Đặt công thức của muối tinh thể là \[F{e_2}{\left( {S{O_4}} \right)_3}.n{H_2}O.\]
Ta có: 0,014.(400 + 18n) = 7,868 ⟹ n = 9.
Công thức của tinh thể là \[F{e_2}{\left( {S{O_4}} \right)_3}.9{H_2}O.\]
Chọn A.
Câu 133:
 Xem đáp án
Xem đáp án
\(Ta\,c\'o :\,\,{n_{KMn{O_4}}} = 0,01 \cdot 0,1 = 0,001\,mol\)
\[\begin{array}{*{20}{l}}{5{H_2}{O_2} + {\rm{ }}2KMn{O_4} + {\rm{ }}3{H_2}S{O_4} \to {K_2}S{O_4} + {\rm{ }}2MnS{O_4} + {\rm{ }}5{O_2} + {\rm{ }}8{H_2}O}\\{\;0,0025 \leftarrow \;0,001\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(mol)\,\,}\end{array}\]
⟹![]()
⟹ Hàm lượng \[{H_2}{O_2}\]trong nước oxy già là
![Để xác định nồng độ dung dịch \[{H_2}{O_2},\]người ta hòa tan 0,5 gam nước oxy già vào nước, thêm \[{H_2}S{O_4}\]tạo môi trường acid. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid6-1721823935.png)
Chọn B.
Câu 134:
 Xem đáp án
Xem đáp án
Muối \[{C_2}{H_8}{O_3}{N_2}\]có chứa 3O nên có thể là muối \(NO_3^ - ,\,CO_3^{2 - },\,HCO_3^ - \).
⟹ CTCT là \[{C_2}{H_5}N{H_3}N{O_3}\]hoặc \[{\left( {C{H_3}} \right)_2}N{H_2}N{O_3}\](do khí sinh ra làm xanh giấy quỳ tím ẩm)
Ta thấy:
\[\begin{array}{*{20}{l}}{X{\rm{ }} + {\rm{ }}NaOH{\rm{ }} \to {\rm{ }}NaN{O_3} + {\rm{ }}Amine + {\rm{ }}{H_2}O}\\{0,1{\rm{ }} \to {\rm{ }}0,1{\rm{ }} \to \;\;\;\;\;{\rm{ }}0,1}\end{array}\]
Vậy chất rắn chứa: \[NaN{O_3}\](0,1 mol) và NaOH dư (0,2 - 0,1 = 0,1 mol)
⟹ m = 0,1.85 + 0,1.40 = 12,5 gam.
Chọn C.
Câu 135:
 Xem đáp án
Xem đáp án
Phản ứng:\[2Fe{\rm{ }} + {\rm{ }}6{H_2}S{O_4} \to F{e_2}{\left( {S{O_4}} \right)_3} + {\rm{ }}3S{O_2} \uparrow + {\rm{ }}6{H_2}O\]
Ta có: \[{n_{Fe}} = 0,12{\rm{ }}mol;{\rm{ }}{n_{{H_2}S{O_4}}} = 0,3{\rm{ }}mol\]
Nhận thấy: \(\frac{{0,12}}{2} > \frac{{0,3}}{6}\)→ Khi phản ứng với \({H_2}S{O_4}\)thì Fe dư và \({H_2}S{O_4}\)hết. Sau đó Fe dư lại phản ứng tiếp với muối \(F{e^{3 + }}\).
\( \Rightarrow {n_{S{O_2}}} = 0,15\,mol\)
\[Fe + F{e_2}{\left( {S{O_4}} \right)_3} \to 3FeS{O_4}\]
Theo đó, muối thu được gồm \(\left\{ \begin{array}{l}FeS{O_4}:a\,mol\\F{e_2}{(S{O_4})_3}:\,b\,mol\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}a + 2b = 0,12\\2a + 2 \cdot 3b = 0,15 \cdot 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 0,06\\b = 0,03\end{array} \right.(mol)\)
Khi hòa tan Cu vào dung dịch X
\(2F{e^{3 + }} + Cu \to C{u^{2 + }} + 2F{e^{2 + }}\)
\(\begin{array}{l} \Rightarrow {n_{Cu}} = \frac{1}{2}{n_{F{e^{3 + }}}} = \frac{1}{2} \cdot 2 \cdot 0,03 = 0,03\,mol\\ \Rightarrow {m_{Cu}} = 0,03 \cdot 64 = 1,92\,gam\end{array}\)
Chọn C.
Câu 136:
Cho các phát biểu sau: Các polymer đều có nhiệt độ nóng chảy xác định (1); đa số polymer không tan trong các dung môi thông thường (2); cao su là vật liệu polymer có tính đàn hồi (3); tơ polyamide bền trong môi trường acid và môi trường base (4); tơ visco và tơ acetate thuộc loại tơ hóa học (5). Số phát biểu đúng là
 Xem đáp án
Xem đáp án
(1) sai, chúng không có nhiệt độ nóng chảy xác định.
(2) đúng.
(3) đúng.
(4) sai, tơ poliamit là tơ có chức -CONH- nên kém bền trong cả acid và base.
(5) đúng, tơ hóa học gồm có tơ tổng hợp và bán tổng hợp.
Vậy có 3 phát biểu đúng.
Chọn B.
Câu 137:
Đồ thị sau biểu diễn thể tích khí nitrogen thu được theo thời gian bằng phản ứng phân huỷ chất chứa nitrogen (hình bên). Dựa vào đồ thị ta thấy từ thời gian x (giây) đến y (giây) phản ứng xảy ra nhanh nhất, khi phản ứng kết thúc thì thu được z (\[c{m^3}\]) khí \({N_2}\). Các giá trị của x, y, z lần lượt là:
![Đồ thị sau biểu diễn thể tích khí nitrogen thu được theo thời gian bằng phản ứng phân huỷ chất chứa nitrogen (hình bên). Dựa vào đồ thị ta thấy từ thời gian x (giây) đến y (giây) phản ứng xảy ra nhanh nhất, khi phản ứng kết thúc thì thu được z (\[c{m^3}\]) khí \({N_2}\). Các giá trị của x, y, z lần lượt là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid7-1721824237.png)
 Xem đáp án
Xem đáp án
- Quan sát đồ thị ta thấy, ở thời điểm từ 20 giây đến 30 giây đường biểu diễn sự phụ thuộc của thể tích khí \[{N_2}\]vào thời gian có độ dốc lớn nhất tức lượng khí \[{N_2}\] được tạo ra là nhiều nhất.
- Quan sát đồ thị ta thấy, từ thời điểm 60 giây trở về sau đường biểu diễn thể tích khí \[{N_2}\] theo thời gian có dạng nằm ngang tức thể tích khí \[{N_2}\] từ thời điểm 60 giây trở đi không có sự tăng thêm thể tích khí \[{N_2}\].
→ Sau thời gian 60 giây thì phản ứng kết thúc và ở thời điểm này thể tích khí \[{N_2}\] là \[90c{m^3}.\]
→ Các giá trị của x, y, z lần lượt là 20, 30, 90.
Chọn B.
Câu 138:
Tiến hành 3 thí nghiệm a, b, c hòa tan cùng lượng m gam Zn vào dung dịch \[{H_2}S{O_4}.\]Khí hydrogen thu được trong mỗi thí nghiệm được biểu diễn bằng đồ thị bên. Phát biểu nào sau đây là đúng?
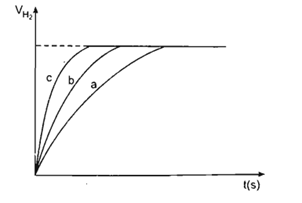
 Xem đáp án
Xem đáp án
- Đường cong c có độ dốc lớn nhất, biểu thị phản ứng xảy ra là nhanh nhất.
- Đường cong b có độ dốc trung bình, biểu thị phản ứng xảy ra trung bình.
- Đường cong a có độ dốc nhỏ nhất, biểu thị phản ứng xảy ra là chậm nhất.
→ Phát biểu đúng: Tiến hành thí nghiệm c và thí nghiệm b ở cùng 1 nhiệt độ, thì zinc ở thí nghiệm c có dạng bột, còn zinc ở thí nghiệm b có dạng lá. Vì zinc ở dạng bột có tốc độ phản ứng xảy ra nhanh hơn zinc ở dạng lá.
Chọn B.
Câu 139:
 Xem đáp án
Xem đáp án
Đề bài cho hỗn hợp \[NaHC{O_3}\]và \[N{a_2}C{O_3}\]tham gia vào 2 quá trình phản ứng sau:
TN1:
TN2:
Đặt số mol \[NaHC{O_3}\]và \[N{a_2}C{O_3}\]trong 25 ml dung dịch A lần lượt là x, y mol.
Thí nghiệm 1:
\({\rm{N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3} + 2{\rm{HCl}} \to 2{\rm{NaCl}} + {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2}{\rm{O}}\) (1)
\({\rm{NaHC}}{{\rm{O}}_3} + {\rm{HCl}} \to {\rm{NaCl}} + {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2}{\rm{O}}\) (2)
\({\rm{HCl}} + {\rm{NaOH}} \to {\rm{NaCl}} + {{\rm{H}}_2}{\rm{O}}\) (3)
→ \[x + 2y = 0,1 - 0,028 = 0,072{\rm{ }}mol\] (4).
Thí nghiệm 2:
\({\rm{BaC}}{{\rm{l}}_2} + {\rm{N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3} \to {\rm{BaC}}{{\rm{O}}_3} + 2{\rm{NaCl}}\) (5)
Sau khi lọc bỏ kết tủa, lấy nước lọc, nước rửa chứa \[NaHC{O_3}\]cho tác dụng với dung dịch HCl:
\({\rm{NaHC}}{{\rm{O}}_3} + {\rm{HCl}} \to {\rm{NaCl}} + {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2}{\rm{O}}\) (6)
→ \[x = 0,026 \cdot 1,0 = 0,026{\rm{ }}mol\]
Thay x vào (4) ta có \[y = 0,023{\rm{ }}mol\]
Vậy nồng độ mol của \[N{a_2}C{O_3}\]là: \({C_{{\rm{M}}\,\,{\rm{(N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3})}} = \frac{{0,023}}{{0,025}} = 0,92{\rm{M}}\)
Nồng độ mol của \[NaHC{O_3}\]là: \({C_{{\rm{M}}\,\,{\rm{(NaHC}}{{\rm{O}}_3})}} = \frac{{0,026}}{{0,025}} = 1,04M\)
Chọn A.
Câu 140:
Hỗn hợp E chứa ba ester mạch hở (không chứa chức khác). Đốt cháy hoàn toàn m gam E cần dùng vừa đủ 1,165 mol \[{O_2}.\]Mặt khác, thủy phân hoàn toàn lượng E trên bằng NaOH thu được hỗn hợp các muối và alcohol. Đốt cháy hoàn toàn lượng muối thu được 11,66 gam \[N{a_2}C{O_3}\]thu được 0,31 mol \[C{O_2},\]còn nếu đốt cháy hoàn toàn lượng alcohol thu được thì cần vừa đủ 0,785 mol \[{O_2}\]thu được 0,71 mol \[{H_2}O.\] Giá trị của m là:
 Xem đáp án
Xem đáp án
Đề bài cho hỗn hợp ester E mạch hở tham gia các phản ứng theo sơ đồ sau:
![Hỗn hợp E chứa ba ester mạch hở (không chứa chức khác). Đốt cháy hoàn toàn m gam E cần dùng vừa đủ 1,165 mol \[{O_2}.\]Mặt khác, thủy phân hoàn toàn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid10-1721824574.png)
- Khi đốt hỗn hợp muối ta có: \({n_{ - {\rm{OH}}}} = {n_{ - {\rm{COO}}}} = {n_{{\rm{NaOH}}}} = 2{n_{{\rm{N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3}}} = 0,22mol\)
- Xét quá trình đốt hoàn toàn lượng alcohol có :
(với \[{n_{ - {\rm{OH}}}} = {n_{ - {\rm{COO}}}} = 0,22\;{\rm{mol}}\])
- Xét quá trình đốt cháy E có:
![Hỗn hợp E chứa ba ester mạch hở (không chứa chức khác). Đốt cháy hoàn toàn m gam E cần dùng vừa đủ 1,165 mol \[{O_2}.\]Mặt khác, thủy phân hoàn toàn (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid9-1721824558.png)
Bảo toàn nguyên tố O ta có:
\(\begin{array}{l}2{n_{ - COO}} + 2{n_{{O_2}}} = 2{n_{C{O_2}}} + {n_{{H_2}O}}\\ \Rightarrow {n_{{H_2}O}} = 2{n_{ - COO}} + 2{n_{{O_2}}} - 2{n_{C{O_2}}} = 2 \cdot 0,22 + 2 \cdot 1,165 - 2 \cdot 0,96 = 0,85\,mol\end{array}\)
Bảo toàn khối lượng ta có:
\({m_E} = {m_{C{O_2}}} + {m_{{H_2}O}} - {m_{{O_2}}} = 0,96 \cdot 44 + 0,85 \cdot 18 - 1,165 \cdot 32 = 20,26\,gam\)
(Ngoài ra: \({m_E} = {m_C} + {m_H} + {m_{O\,\,( - COO)}}\))
Đáp án: 20,26
Câu 141:
 Xem đáp án
Xem đáp án
Sinh sản bằng hình thức trinh sinh ở động vật không xương sống như ong, kiến, rệp... và ở động vật có xương sống ở một số loài cá, lưỡng cư, bò sát… Chọn A.
Câu 142:
 Xem đáp án
Xem đáp án
Dựa vào tính toàn năng của tế bào thực vật, từ một tế bào hoặc một mô thực vật có thể nuôi cấy để phát triển thành một cây hoàn chỉnh thông qua quá trình nguyên phân. Chọn A.
Câu 143:
 Xem đáp án
Xem đáp án
Gia súc là sinh vật hằng nhiệt, cơ thể có cơ chế tự điều hòa để ổn định thân nhiệt duy trì hoạt động sinh lí bình thường của cơ thể. Khi đến mùa rét nhiệt độ môi trường thấp, cơ thể mất nhiều nhiệt vào môi trường và để bù lại lượng nhiệt bị mất cơ thể phải tăng cường chuyển hóa cung cấp thêm năng lượng. Chọn C.
Câu 144:
 Xem đáp án
Xem đáp án
Hai chuỗi pôlynuclêôtit trong phân tử ADN liên kết với nhau bằng liên kết hiđrô giữa A – T; G – X. Chọn D.
Câu 145:
 Xem đáp án
Xem đáp án
Người ta thường áp dụng phương pháp tạo giống cây trồng tam bội để tăng năng suất cho những cây trồng thu hoạch cơ quan sinh dưỡng như: dưa hấu, nho, củ cải đường. Ngược lại, đối với những cây trồng thu hoạch hạt như đậu tương thì không được áp dụng phương pháp này do thể tam bội bất thụ (giảm năng suất hạt). Chọn D.
Câu 146:
 Xem đáp án
Xem đáp án
A, C. Sai. Nếu là đột biến thì sẽ xảy ra cách đơn lẻ và ngẫu nhiên nhưng trong trường hợp này, các cá thể thỏ thuộc giống thỏ Himalaya đều có kiểu hình này nên đây không phải là đột biến.
B. Sai. Trong thí nghiệm buộc cục nước đá vào cơ thể thỏ, không hề có sự xuất hiện của kẻ thù, vật ăn thịt nhưng màu lông vẫn thay đổi. Đồng thời, thỏ không thể tự đổi màu lông theo ý.
D. Đúng. Gen quy định tổng hợp sắc tố lông bị ảnh hưởng bởi nhiệt độ vì trong thí nghiệm, khi cạo phần lông màu trắng đi và áp cục nước đá vào vị trí bị cạo, lông mọc ra có màu đen.
Chọn D.
Câu 147:
 Xem đáp án
Xem đáp án
Di – nhập gen là nhân tố tiến hóa có thể mang đến quần thể những alen mới làm phong phú thêm vốn gen của quần thể trong trường hợp những cá thể nhập cư vào quần thể mang những alen chưa có trong quần thể ban đầu. Chọn B.
Câu 148:
 Xem đáp án
Xem đáp án
Nhờ điều kiện khí hậu thích hợp, rừng nhiệt đới có độ đa dạng về thành phần loài và số lượng cá thể trong loài. Do đó, khu sinh học có độ đa dạng sinh học cao nhất là rừng mưa nhiệt đới. Chọn A.
Câu 149:
Phả hệ sau đây mô tả sự di truyền bệnh phêninkêtô niệu ở người do một trong hai alen của một gen quy định. Theo lí thuyết, có tối đa bao nhiêu người trong phả hệ sau xác định được chính xác kiểu gen?
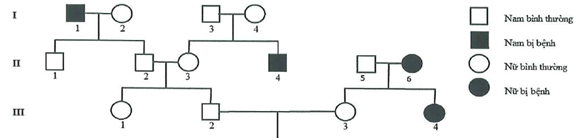
 Xem đáp án
Xem đáp án
Bệnh phêninkêtô niệu ở người do gen lặn quy định. Quy ước gen: A – bình thường; a – bị bệnh.
→ Tất cả những người bị bệnh (I.1, II.4, II.6, III.4) đều có kiểu gen đồng hợp lặn (aa).
I.3 × I.4 đều bình thường nhưng sinh ra con bị bệnh → Cơ thể I.3; I.4 có mang alen gây bệnh (Aa).
I.1 có kiểu gen đồng hợp lặn aa → Các con của I.1 dù bình thường nhưng vẫn mang gen lặn a do nhận 1 giao tử (a) từ bố → II.1; II.2 có kiểu gen dị hợp Aa.
II.6 có kiểu gen đồng hợp lặn aa → Các con của II.6 dù bình thường nhưng vẫn mang gen lặn a do nhận 1 giao tử (a) từ mẹ → III.3 có kiểu gen dị hợp Aa.
II.5 × II.6 sinh ra con bị bệnh → Cơ thể II.5 có mang alen gây bệnh (Aa).
Vậy có tối đa 10 người trong phả hệ sau xác định được chính xác kiểu gen. Chọn A.
Câu 150:
Xét 4 tế bào sinh tinh ở cơ thể có kiểu gen \[{\rm{Aa}}\frac{{{\rm{BD}}}}{{{\rm{bd}}}}\] giảm phân tạo giao tử. Cho biết các gen liên kết hoàn toàn, trong quá trình giảm phân chỉ có 1 tế bào có cặp NST mang 2 cặp gen B, b và D, d không phân li trong giảm phân I, phân li bình thường trong giảm phân II; cặp NST mang cặp gen A, a phân li bình thường. Kết thúc quá trình giảm phân đã tạo ra 6 loại giao tử, trong đó có 37,5% loại giao tử mang 2 alen trội. Theo lí thuyết, loại giao tử mang 1 alen trội chiếm tỉ lệ là bao nhiêu?
 Xem đáp án
Xem đáp án
Kiểu gen \[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\] giảm phân không phân li ở giảm phân I, giảm phân II bình thường sẽ tạo giao tử (\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\]) và giao tử (O). Vậy tế bào sinh tinh giảm phân bị rối loạn sẽ tạo giao tử:
(A, a)(\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\], O) = 2 A\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\] và 2 a hoặc 2 A và 2 a\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\].
Tế bào sinh tinh bình thường tạo giao tử (A, a)(BD, bd) = 2 ABD và 2 abd (kiểu 1) hoặc 2 Abd và 2 aBD (kiểu 2).
Mà 4 tế bào sinh tinh giảm phân được 6 loại giao tử, tức là 4 (bình thường) + 2 (đột biến). Như vậy, với 3 tế bào sinh tinh giảm phân bình thường ta có 2 trường hợp là: 2 tế bào kiểu 1, 1 tế bào kiểu 2 hoặc 1 tế bào kiểu 1, 2 tế bào kiểu 2.
Theo bài ra, 4 tế bào giảm phân thu được 16 giao tử, giao tử 2 alen trội chiếm 3/8 = 6/16.
|
Trường hợp |
ABD |
abd |
aBD |
Abd |
Tỉ lệ 2 trội thiếu |
|
1 tế bào kiểu 1, 2 tế bào kiểu 2 |
2 |
2 |
4 |
4 |
2 |
|
2 tế bào kiểu 1, 1 tế bào kiểu 2 |
4 |
4 |
2 |
2 |
4 (loại) |
Vậy có 1 tế bào giảm phân bình thường kiểu 1, 2 tế bào giảm phân bình thường kiểu 2 và tế bào rối loạn tạo giao tử 2 A và 2 a\[\frac{{B{\rm{D}}}}{{b{\rm{d}}}}\].
Vậy tỉ lệ giao tử mang 1 alen trội là (4 Abd + 2A)/16 = 6/16 = 37,5%. Đáp án: 37,5%.
