Phóng xạ
-
973 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm phát biểu sai về hiện tượng phóng xạ
Xem đáp án
A, B, C - đúng
D -sai vì: Hằng số phóng xạ \[\lambda = \frac{{\ln 2}}{T}\]
Đáp án cần chọn là: D
Câu 2:
Đại lượng nào của chất phóng xạ không biến thiên cùng quy luật với các đại lượng còn lại nêu sau đây
Xem đáp án
Ta có:
+ Số hạt nhân phóng xạ còn lại: \[N = {N_0}{2^{ - \frac{t}{T}}}\]
+ Số mol chất phóng xạ còn lại: \[{n_{(t)}} = \frac{{{m_{(t)}}}}{A} = \frac{{{m_0}{{.2}^{ - \frac{t}{T}}}}}{A}\]
+ Khối lượng của chất đã phân rã: \[{\rm{\Delta }}m = {m_0}(1 - {2^{ - \frac{t}{T}}})\]
+ Độ phóng xạ của lượng chất còn lại: \[H = \frac{{{H_0}}}{{{2^{\frac{t}{T}}}}} = {H_0}{.2^{ - \frac{t}{T}}}\]
=>Khối lượng của lượng chất đã phân rã không biến thiên cùng quy luật với các đại lượng còn lại
Đáp án cần chọn là: C
Câu 3:
Coban \[{}_{27}^{60}Co\] là chất phóng xạ có chu kì bán rã T = 5,33 năm. Lúc đầu có 1000g Co thì sau 10,66 năm số nguyên tử coban còn tại là?
Xem đáp án
Khối lượng Co còn lại sau 10,66 năm là:
\[m = {m_0}{.2^{ - \frac{t}{T}}} = {1000.2^{ - \frac{{10,66}}{{5,33}}}} = 250g\]
Số nguyên tử Coban còn lại là:
\[N = \frac{m}{A}.{N_A} = \frac{{250}}{{60}}{.6,02.10^{23}} = {2,51.10^{24}}\]
Đáp án cần chọn là: A
Câu 4:
Một chất phóng xạ có chu kì bán rã là 3,8 ngày. Số hạt nhân sẽ bị phân rã hết 70% sau thời gian là
Xem đáp án
Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \[N = {N_0}{.2^{\frac{{ - t}}{T}}}\]
Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:
\[\begin{array}{*{20}{l}}{N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}}) = 70{\rm{\% }}{N_0}}\\{ \Rightarrow (1 - {2^{\frac{{ - t}}{T}}}) = 70{\rm{\% }} = 0,7 \Rightarrow {2^{\frac{{ - t}}{T}}} = 0,3}\\{ \Rightarrow t = - T.{{\log }_2}(0,3) = 1,74T = 1,74.3,8 = 6,6}\end{array}\]
Vậy thời gian là 6,6 ngày.
Đáp án cần chọn là: A
Câu 5:
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã T của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \[\Delta N\] và số hạt ban đầu N0. Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?
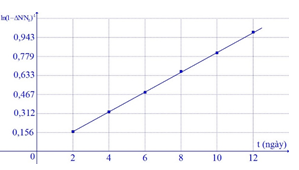
Xem đáp án
Ta có: \[N = {N_0}{e^{ - \lambda t}} \Rightarrow \] Số hạt bị phân rã là:
\[{\rm{\Delta }}N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}(1 - {e^{ - \lambda t}})\]
\[ \Rightarrow \frac{{{\rm{\Delta }}N}}{{{N_0}}} = 1 - {e^{ - \lambda t}} \Rightarrow 1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}} = {e^{ - \lambda t}}\]
\[ \Rightarrow \frac{1}{{\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)}} = {e^{\lambda t}} \Rightarrow \ln {\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\]
Từ đồ thị ta thấy \[\lambda \approx 0,078\]
\[ \Rightarrow T = \frac{{\ln 2}}{\lambda } \approx 8,9\]Đáp án cần chọn là: B
Câu 6:
Một lượng chất phóng xạ sau 12 năm thì còn lại 1/16 khối lượng ban đầu của nó. Chu kì bán rã của chất đó là
Xem đáp án
Ta có \[\frac{m}{{{m_0}}} = \frac{1}{{{2^{\frac{t}{T}}}}} = \frac{1}{{16}} = \frac{1}{{{2^4}}}\]
\[ \to \frac{t}{T} = 4 \Rightarrow T = \frac{t}{4} = \frac{{12}}{4} = 3\] năm
Đáp án cần chọn là: A
Câu 7:
Một chất phóng xạ có chu kỳ bán rã là 3,8 ngày. Sau thời gian 11,4 ngày thì độ phóng xạ (hoạt độ phóng xạ) của lượng chất phóng xạ còn lại bằng bao nhiêu phần trăm so với độ phóng xạ của lượng chất phóng xạ ban đầu?
Xem đáp án
T = 3,8 ngày ; t = 11,4 = 3T ngày. Do đó ta đưa về hàm mũ để giải nhanh như sau :
\[H = {H_0}{.2^{ - \frac{t}{T}}} \Leftrightarrow \frac{H}{{{H_0}}} = {2^{ - \frac{t}{T}}} \Leftrightarrow \frac{H}{{{H_0}}} = {2^{ - 3}} = \frac{1}{8} = {\rm{ }}12,5\% \]
Đáp án cần chọn là: C