Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
-
388 lượt thi
-
150 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Một nhóm học sinh lớp 10 trả lời một cuộc khảo sát về khoá học toán mà họ đang theo học. Dữ liệu khảo sát được chia nhỏ như trong bảng sau:
|
|
Môn học |
Tổng |
|||
|
Đại số I |
Hình học |
Đại số II |
|||
|
Giới tính |
Nữ |
35 |
53 |
62 |
150 |
|
Nam |
44 |
59 |
57 |
160 |
|
|
Tổng cộng |
79 |
112 |
119 |
310 |
|
Đáp án nào dưới đây chiếm khoảng 19% tổng số người trả lời khảo sát?
 Xem đáp án
Xem đáp án
Câu 2:
Trong không gian \[Oxyz,\] gọi \[a,\,\,b,\,\,c\] lần lượt là khoảng cách từ điểm đến các mặt phẳng tọa độ là Giá trị biểu thức bằng\(M\left( {1\,;\,\,3\,;\,\,2} \right)\)
 Xem đáp án
Xem đáp án
Với \(A\left( {{x_0}\,;\,\,{y_0}\,;\,\,{z_0}} \right) \in \left( {Oxyz} \right)\).
Khi đó \(d\left( {A,\,\,\left( {Oxy} \right)} \right) = {z_0}\,,\,\,d\left( {A,\,\,\left( {Oxz} \right)} \right) = {y_0}\,,\,\,d\left( {A,\,\,\left( {Oyz} \right)} \right) = {x_0}.\)
Theo bài ra ta có: \(a = d\left( {M,\,\,\left( {Oxy} \right)} \right) = 2\,;\,\,b = d\left( {M,\,\,\left( {Oyz} \right)} \right) = 1\,;\,\,c = d\left( {M,\,\,\left( {Oxz} \right)} \right) = 3.\)
Suy ra \(P = a + {b^2} + {c^3} = 2 + {1^2} + {3^3} = 30.\) Chọn C.
Câu 3:
Cho số phức \(z\) thỏa mãn \(2z - i \cdot \bar z = 3i.\) Môđun của \(z\) bằng
 Xem đáp án
Xem đáp án
Ta đặt \(z = a + bi.\)
\(2z - i \cdot \bar z = 3i \Leftrightarrow 2\left( {a + bi} \right) - i\left( {a - bi} \right) = 3i\)
\( \Leftrightarrow 2a - b + i\left( {2b - a} \right) = 3i \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2a - b = 0}\\{2b - a = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 2}\end{array}} \right.} \right.\).
Từ đó ta suy ra: \(\left| z \right| = \sqrt {{a^2} + {b^2}} = \sqrt 5 .\) Chọn A.
Câu 4:
Một chất điểm chuyển động có phương trình \(s = f\left( t \right) = \frac{1}{3}{t^3} - {t^2} + 4t + 5\) (\(s\) được tính bằng mét, \(t\) được tính bằng giây). Gia tốc chuyển động của chất điểm tại thời điểm \(t = 2\) giây là
 Xem đáp án
Xem đáp án
Phương trình gia tốc: \(a = s'' = f''\left( t \right) = 2t - 2\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\)
Tại \(t = 2\) thì \(a\left( 2 \right) = 2 \cdot 2 - 2 = 2\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\). Chọn D.
Câu 5:
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = AA' = a\,,\,\,AC = 2a.\) Khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ACD'} \right)\) bằng
 Xem đáp án
Xem đáp án
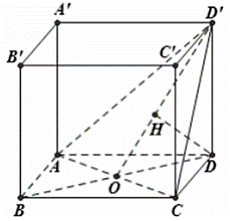
Kẻ \(DH \bot OD'\).
Ta có \[\left\{ \begin{array}{l}AC \bot OD\\AC \bot DD'\end{array} \right. \Rightarrow AC \bot \left( {DOD'} \right) \Rightarrow AC \bot DH\].
Mà \(DH \bot OD'\) nên \(DH \bot \left( {ACD'} \right) \Rightarrow DH = d\left( {D,\,\,\left( {ACD'} \right)} \right)\).
Ta có \(OD = \frac{1}{2}BD = \frac{1}{2}AC = a\) nên
\(\frac{1}{{D{H^2}}} = \frac{1}{{D{{D'}^2}}} + \frac{1}{{O{D^2}}} = \frac{2}{{{a^2}}} \Rightarrow DH = \frac{{a\sqrt 2 }}{2}{\rm{. }}\)Chọn D.Câu 6:
Trong không gian \[Oxyz,\] phương trình của đường thẳng \(d\) đi qua điểm \(A\left( {1\,;\,\,2\,;\,\, - 5} \right)\) và vuông góc với mặt phẳng \((P):2x + 3y - 4z + 5 = 0\) là
 Xem đáp án
Xem đáp án
Đường thẳng \(d\) đi qua điểm \(A\left( {1\,;\,\,2\,;\,\, - 5} \right)\) và vuông góc với mặt phẳng \((P):2x + 3y - 4z + 5 = 0\) nên nhận \(\vec u = \left( {2\,;\,\,3\,;\,\, - 4} \right)\) là vectơ chỉ phương.
Phương trình đường thẳng \(d\) là \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 2 + 3t}\\{z = - 5 - 4t}\end{array}} \right..\) Chọn C.
Câu 7:
Gọi \[M,\,\,N\] lần lượt là giao điểm của đường thẳng \(y = x + 1\) và đường cong \(y = \frac{{2x + 4}}{{x - 1}}.\) Khi đó hoành độ trung điểm \[I\] của đoạn \[MN\] bằng
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của hai đồ thị là
\(\frac{{2x + 4}}{{x - 1}} = x + 1\,\,\left( {x \ne 1} \right) \Leftrightarrow {x^2} - 2x - 5 = 0\). Khi đó \({x_t} = \frac{{{x_M} + {x_N}}}{2} = \frac{{ - \left( { - 2} \right)}}{2} = 1.\)
Ta giải nghiệm rồi tìm được \(x = 1 \pm \sqrt 6 \Rightarrow {x_t} = 1.\) Chọn B.
Câu 8:
Cho hình chóp \[S.ABC\] có đáy là tam giác đều cạnh \(2a,\,\,SA \bot \left( {ABC} \right).\) Góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \(30^\circ .\) Thể tích khối chóp \[S.ABC\] là
 Xem đáp án
Xem đáp án
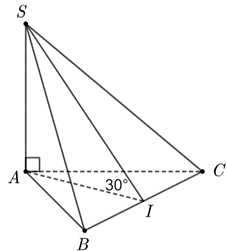
Gọi \(I\) là trung điểm BC.
Ta có \(\left( {\left( {SBC} \right),\,\,\left( {ABC} \right)} \right) = \widehat {SIA} = 30^\circ \)
\( \Rightarrow \Delta SIA\) có \(SA = AI \cdot \tan 30^\circ = 2a \cdot \frac{{\sqrt 3 }}{2} \cdot \frac{{\sqrt 3 }}{3} = a.\)
\(V = \frac{1}{3}{S_{ABC}} \cdot SA = \frac{1}{3} \cdot \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{3}.\) Chọn B.Câu 9:
Với \(a\) là số thực dương tuỳ ý, đặt \({\log _2}a = m.\) Khi đó \(\log _2^2\left( {8{a^2}} \right)\) bằng
 Xem đáp án
Xem đáp án
Ta có \(\log _2^2\left( {8{a^2}} \right) = {\left( {{{\log }_2}\left( {8a} \right)} \right)^2} = {\left( {{{\log }_2}8 + {{\log }_2}{a^2}} \right)^2}\)
\( = {\left( {3 + 2m} \right)^2} = 4{m^2} + 12m + 9.{\rm{ }}\)Chọn A.
Câu 10:
Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x + 5}}{2} = \frac{{y - 7}}{{ - 2}} = \frac{z}{1}\) và điểm \(I\left( {4\,;\,\,1\,;\,\,6} \right).\) Đường thẳng \(d\) cắt mặt cầu \(\left( S \right)\) có tâm \(I\) tại hai điểm \[A,\,\,B\] sao cho \(AB = 6.\) Phương trình của mặt cầu \(\left( S \right)\) là
 Xem đáp án
Xem đáp án
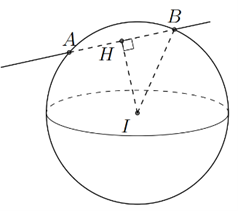
Đường thẳng \(d\) đi qua \(M\left( { - 5\,;\,\,7\,;\,\,0} \right)\) và vectơ chỉ phương \(\vec u = \left( {2\,;\,\, - 2\,;\,\,1} \right).\)
Gọi \(H\) là hình chiếu của \(I\) trên \(\left( d \right).\)
Ta có \(IH = d\left( {I,\,\,AB} \right) = \frac{{\left| {\left[ {\vec u\,,\,\,\overrightarrow {MI} } \right]} \right|}}{{\left| {\vec u} \right|}} = 3\)
\( \Rightarrow R = \sqrt {I{H^2} + {{\left( {\frac{{AB}}{2}} \right)}^2}} = 18\).
Vậy \(\left( S \right):{\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 6} \right)^2} = 18.\) Chọn A.Câu 11:
Tìm tất cả các giá trị thực của tham số \(m\) thì phương trình \(m{x^2} - 2\left( {m - 2} \right)x + m - 3 = 0\) có hai nghiệm dương phân biệt?
 Xem đáp án
Xem đáp án
Phương trình \(m{x^2} - 2\left( {m - 2} \right)x + m - 3 = 0\) có 2 nghiệm dương phân biệt
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a \ne 0}\\{\Delta ' > 0}\\{S > 0}\\{P > 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ne 0}\\{{{\left( {m - 2} \right)}^2} - m\left( {m - 3} \right) > 0}\\{\frac{{2\left( {m - 2} \right)}}{m} > 0}\\{\frac{{m - 3}}{m} > 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ne 0}\\{ - m + 4 > 0}\\{m \in \left( { - \infty \,;\,\,0} \right) \cup \left( {2\,;\,\, + \infty } \right)}\\{m \in \left( { - \infty \,;\,\,0} \right) \cup \left( {3\,;\,\, + \infty } \right)}\end{array}} \right.\)
\( \Leftrightarrow m \in \left( { - \infty \,;\,\,0} \right) \cup \left( {3\,;\,\,4} \right).\) Chọn C.
Câu 12:
Cho hàm số \(f\left( x \right) = \frac{{mx - 2}}{{m + 1 - x}}\) với \(m\) là tham số. Số giá trị nguyên thuộc khoảng \(\left( { - 10\,;\,\,10} \right)\) để hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0\,;\,\, + \infty } \right)\) là
 Xem đáp án
Xem đáp án
Ta có \(f\left( x \right) = \frac{{mx - 2}}{{ - x + m + 1}} \Rightarrow f'\left( x \right) = \frac{{{m^2} + m - 2}}{{{{\left( { - x + m + 1} \right)}^2}}}\).
Yêu cầu bài toán \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{f'\left( x \right) > 0}\\{ - x + m + 1 \ne 0}\end{array};\,\,\forall x \in \left( {0\,;\,\, + \infty } \right)} \right.\).
Kết hợp với: \(m \in \left( { - 10\,;\,\,10} \right)\) và \(m \in \mathbb{Z}\) suy ra \(m \in \left\{ { - 9\,;\,\, - 8\,;\,\, - 7\,;\,\, \ldots \,;\,\, - 3} \right\}.\) Chọn A.
Câu 13:
Ngày thứ nhất cửa hàng bán được 10 cốc nước mía, ngày sau bán nhiều hơn ngày hôm trước đó 1 cốc nước mía. Hỏi ngày thứ 10 cửa hàng sẽ bán được bao nhiêu cốc nước mía?
 Xem đáp án
Xem đáp án
Số cốc mỗi ngày cửa hàng bán được lần lượt lập thành cấp số cộng có công sai là \(d = 1\) và \({u_1} = 10.\)
Do đó, ngày thứ 10 cửa hàng sẽ bán được số cốc nước mía là: \({u_{10}} = {u_1} + 9d = 10 + 9 = 19.\)
Chọn C.
Câu 14:
Có bao nhiêu số nguyên \(x\) thỏa mãn \({\log _2}\frac{{{x^2} - 1}}{{81}} < {\log _3}\frac{{{x^2} - 1}}{{16}}\)?
 Xem đáp án
Xem đáp án
Điều kiện: \({x^2} - 1 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x > 1}\\{x < - 1}\end{array}} \right..\)
Ta có \({\log _2}\frac{{{x^2} - 1}}{{81}} < {\log _3}\frac{{{x^2} - 1}}{{16}}\)
\( \Leftrightarrow {\log _2}\left( {{x^2} - 1} \right) - {\log _2}81 < {\log _3}\left( {{x^2} - 1} \right) - {\log _3}16\)
\( \Leftrightarrow {\log _2}3 \cdot {\log _3}\left( {{x^2} - 1} \right) - 4{\log _2}3 < {\log _3}\left( {{x^2} - 1} \right) - 4{\log _3}2\)
\( \Leftrightarrow \left( {{{\log }_2}3 - 1} \right){\log _3}\left( {{x^2} - 1} \right) < 4\left( {{{\log }_2}3 - {{\log }_3}2} \right)\)
\( \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < \frac{{4\left( {{{\log }_2}3 - {{\log }_3}2} \right)}}{{{{\log }_2}3 - 1}}\)\( \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < \frac{{4\left( {\frac{1}{{{{\log }_3}2}} - {{\log }_3}2} \right)}}{{\frac{1}{{{{\log }_3}2}} - 1}}\)
\( \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < 4\left( {1 + {{\log }_3}2} \right) \Leftrightarrow {\log _3}\left( {{x^2} - 1} \right) < {\log _3}{6^4}\)
\( \Leftrightarrow 0 < {x^2} - 1 < {6^4} \Leftrightarrow \left[ \begin{array}{l}1 < x < \sqrt {1297} \\ - \sqrt {1297} < x < - 1\end{array} \right.\).
Vì \(x\) là số nguyên nên \[x \in \left\{ { - 36\,;\,\, - 35\,;\,\, \ldots ;\,\, - 2\,;\,\,2\,;\,\, \ldots ;\,\,35\,;\,\,36} \right\}.\]
Vậy có 70 số nguyên \(x\) thỏa mãn yêu cầu bài toán. Chọn C.
Câu 15:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = - \frac{1}{{{x^2}}} + 2\) và \(f(2) = \frac{9}{2}.\) Biết \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right)\) thỏa mãn \[F\left( 2 \right) = 4 + \ln 2\], khi đó \(F(1)\) bằng
 Xem đáp án
Xem đáp án
Ta có \(f'\left( x \right) = - \frac{1}{{{x^2}}} + 2 \Rightarrow f\left( x \right) = \frac{1}{x} + 2x + C.\)
Theo bài ra \(f\left( 2 \right) = \frac{9}{2} \Rightarrow \frac{1}{2} + 4 + C = \frac{9}{2} \Rightarrow C = 0.\)
\( \Rightarrow f\left( x \right) = \frac{1}{x} + 2x \Rightarrow F\left( x \right) = \ln \left| x \right| + {x^2} + M\)
Lại có \(F\left( 2 \right) = 4 + \ln 2 \Rightarrow \ln 2 + 4 + M = 4 + \ln 2\)
\[ \Rightarrow M = 0 \Rightarrow F\left( x \right) = \ln \left| x \right| + {x^2} \Rightarrow F\left( 1 \right) = 1.\] Chọn C.
Câu 16:
Tổng các nghiệm nguyên của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{5x - 2 < 4x + 5}\\{{x^2} < {{\left( {x + 2} \right)}^2}}\end{array}} \right.\) bằng
 Xem đáp án
Xem đáp án
Ta có \(\left\{ {\begin{array}{*{20}{l}}{5x - 2 < 4x + 5}\\{{x^2} < {{\left( {x + 2} \right)}^2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x < 7}\\{{x^2} < {x^2} + 4x + 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x < 7}\\{ - 4x < 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x < 7}\\{x > - 1}\end{array}} \right.} \right.} \right.} \right.\).
Vậy tập nghiệm của hệ bất phương trình là \[S = \left( { - 1\,;\,\,7} \right).\]
Suy ra các nghiệm nguyên của hệ bất phương trình là \[0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6.\]
Vậy tổng tất cả các nghiệm của hệ bất phương trình là 21. Chọn A.
Câu 17:
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \[h\left( t \right) = 29 + 3\sin \left[ {\frac{\pi }{{12}}\left( {t - 9} \right)} \right]\] với \(h\) tính bằng độ \(C\) và \(t\) là thời gian trong ngày tính bằng giờ. Thời gian nhiệt độ cao nhất trong ngày là
 Xem đáp án
Xem đáp án
Ta có \( - 1 \le \sin \frac{\pi }{{12}}\left( {t - 9} \right) \le 1\)
\( \Leftrightarrow - 3 \le 3\sin \frac{\pi }{{12}}\left( {t - 9} \right) \le 3\)\( \Leftrightarrow 26 \le 29 + 3\sin \frac{\pi }{{12}}\left( {t - 9} \right) \le 32.\)
Do đó nhiệt độ cao nhất trong ngày là 32 độ \(C\) khi
\(\sin \frac{\pi }{{12}}\left( {t - 9} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}\left( {t - 9} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 15 + 24k\,\,\left( {k \in \mathbb{Z}} \right){\rm{. }}\)
Do \(0 \le t \le 24\) nên \(k = 0\) suy ra \(t = 15\).
Vậy lúc 15 giờ là thời gian nhiệt độ cao nhất trong ngày. Chọn B.
Câu 18:
Cho \({z_1} = 2m + \left( {m - 2} \right)i\) và \({z_2} = 3 - 4mi\), với \(m\) là tham số thực. Biết \({z_1}{z_2}\) là số thuần ảo. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Ta có \({z_1}{z_2} = \left[ {2m + \left( {m - 2} \right)i} \right]\left( {3 - 4mi} \right)\)\( = 2m \cdot 3 - 8{m^2}i + 3\left( {m - 2} \right)i - 4m\left( {m - 2} \right){i^2}\)
\( = 2m - 8{m^2} \cdot i + 3\left( {m - 2} \right)i + 4m\left( {m - 2} \right)\)\( = 4{m^2} - 6m + \left( { - 8{m^2} + 3m - 6} \right)i\) là số thuần ảo.
Khi đó \(4{m^2} - 6m = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 0}\\{m = \frac{3}{2}}\end{array}} \right..\) Chọn A.
Câu 19:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có bảng biến thiên như hình vẽ dưới. Hỏi hàm số \(g\left( x \right) = f\left( {2x} \right) - x\) có bao nhiêu điểm cực trị?
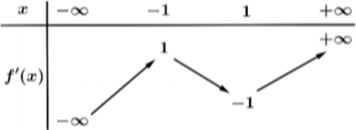
 Xem đáp án
Xem đáp án
Ta có \[g'\left( x \right) = {\left( {2x} \right)^\prime } \cdot f'\left( {2x} \right) - 1 = 2f'\left( {2x} \right) - 1\]
Dựa vào bảng biến thiên, ta được \(f'\left( t \right) = \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = {t_1} \in \left( { - \infty \,;\,\, - 1} \right)}\\{t = {t_2} \in \left( { - 1\,;\,\,1} \right)}\\{t = {t_3} \in \left( {1\,;\,\, + \infty } \right)}\end{array}} \right.\).
Do đó hàm số đã cho có 3 điểm cực trị. Chọn D.
Câu 20:
Anh Duy làm bồi bàn tại một nhà hàng ở Hà Nội. Với mỗi bàn phục vụ anh ấy có thể kiếm được 15 hóa đơn. Trong bữa trưa, anh ấy phục vụ 12 bàn và mỗi bàn có hóa đơn trung bình là \[500\,\,000\] đồng. Biết vào buổi tối, mỗi bàn có hóa đơn trung bình là \[900\,\,000\] đồng. Số bàn tối thiểu mà anh ấy cần phục vụ để kiếm được ít nhất \[3\,\,600\,\,000\] đồng trong ngày là
 Xem đáp án
Xem đáp án
Số bàn anh Duy phục vụ trong bữa tối là \(t\,\,\left( {t \in \mathbb{N}} \right).\)
Số tiền anh Duy kiếm được trong bữa trưa là: \(15\% \cdot 12 \cdot 500\,\,000 = 900\,\,000\) (đồng)
Số tiền anh Duy kiếm được trong bữa tối là: \[15\% \cdot t \cdot 900\,\,000 = t \cdot 135\,\,000\] (đồng)
Tổng số tiền anh Duy kiếm được trong ngày là: \(900\,\,000 + t \cdot 135\,\,000\) (đồng)
Anh Duy kiếm được ít nhất \[3\,\,600\,\,000\] đồng mỗi ngày khi
\(900\,\,000 + t \cdot 135\,\,000 \ge 3\,\,600\,\,000 \Leftrightarrow t \ge 20.\)
Vậy số bàn tối thiểu thỏa yêu cầu bài toán là \(t + 12 = 20 + 12 = 32.\) Chọn A.
Câu 21:
Cắt hình trụ \[\left( T \right)\] bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng \(30\,\;{\rm{c}}{{\rm{m}}^2}\) và chu vi bằng \(26\;\,{\rm{cm}}.\) Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ \[\left( T \right)\]. Diện tích toàn phần của \[\left( T \right)\] là
 Xem đáp án
Xem đáp án
Gọi \[h,\,\,r\] lần lượt là đường cao và bán kính đáy của hình trụ \[\left( T \right)\].
Thiết diện của mặt phẳng và hình trụ \[\left( T \right)\] là hình chữ nhật \[ABCD\].
Khi đó theo giả thiết ta có
\(\left\{ {\begin{array}{*{20}{l}}{h > 2r}\\{{S_{ABCD}} = h \cdot 2r = 30}\\{{C_{ABCD}} = 2\left( {h + 2r} \right) = 26}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{h > 2r}\\{hr = 15}\\{h + 2r = 13}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{h > 2r}\\{h = 13 - 2r}\\{ - 2{r^2} + 15r - 15 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{h > 2r}\\{r = \frac{3}{2}.}\\{h = 10}\end{array}} \right.} \right.} \right.} \right.\)
Vậy \({S_{TP}} = {S_{XQ}} + 2S = 2\pi rh + 2\pi {r^2} = 2\pi \frac{3}{2}10 + 2\pi {\left( {\frac{3}{2}} \right)^2} = \frac{{69\pi }}{2}\left( {\;{\rm{c}}{{\rm{m}}^2}} \right).\) Chọn C.
Câu 22:
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2\,;\,\,3} \right]\) để hàm số \(y = {x^3} - \frac{3}{2}\left( {2m - 3} \right){x^2} + m + 2\) có hai điểm cực trị và hoành độ điểm cực tiểu nhỏ hơn 2?
 Xem đáp án
Xem đáp án
Ta có \(y' = 3{x^2} - 3\left( {2m - 3} \right)x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2m - 3}\end{array}} \right.\)
Để hàm số đã cho có hai điểm cực trị \( \Leftrightarrow 2m - 3 \ne 0 \Leftrightarrow m \ne \frac{3}{2}.\)
Vì hoành độ điểm cực tiểu nhỏ hơn 2 nên \(2m - 3 < 2 \Leftrightarrow m < \frac{5}{2}.\)
Kết hợp với \(m \in \left[ { - 2\,;\,\,3} \right]\) và \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2} \right\}.\) Chọn A.
Câu 23:
Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng
 Xem đáp án
Xem đáp án
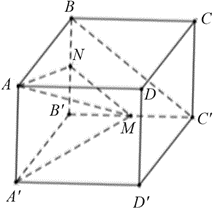
Giả sử cạnh của hình lập phương là \(a > 0.\)
Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)
Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {\widehat {AM\,;\,\,BC'}} \right) = (\widehat {AM\,;\,MN}).\)
Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có
\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)
Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]
Trong tam giác \[AMN\] ta có
\(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\)
Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.
Câu 24:
Trong không gian \[Oxyz,\] cho hai điểm \(A\left( {2\,;\,\, - 2\,;\,\,1} \right),\,\,B\left( {0\,;\,\,1\,;\,\,2} \right).\) Tọa độ của điểm \(M\) thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho ba điểm \[A,\,\,B,\,\,M\] thẳng hàng là
 Xem đáp án
Xem đáp án
Ta có \(M \in \left( {Oxy} \right) \Rightarrow M\left( {x\,;\,\,y\,;\,\,0} \right) \Rightarrow \overrightarrow {AB} = \left( { - 2\,;\,\,3\,;\,\,1} \right)\) và \(\overrightarrow {AM} = (x - 2;y + 2; - 1).\)
Để A, B, M thẳng hàng thì \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng phương.
Khi đó \(\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{3} = \frac{{ - 1}}{1} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = - 5}\end{array}} \right..\)
Vậy \[M\left( {4\,;\,\, - 5\,;\,\,0} \right).\] Chọn A.
Câu 25:
Trên mặt phẳng tọa độ \[Oxy,\] cho điểm \(I\left( {1\,;\,\, - 1} \right)\) và hai đường thẳng \({d_1}:x + y - 3 = 0\), \({d_2}:x - 2y - 6 = 0.\) Hai điểm \[A,\,\,B\] lần lượt thuộc hai đường thẳng \({d_1},\,\,{d_2}\) sao cho \(I\) là trung điểm của đoạn thẳng \[AB.\] Đường thẳng \[AB\] có một vectơ chỉ phương là
 Xem đáp án
Xem đáp án
Vì \(A \in {d_1}\), \(B \in {d_2}\) nên ta giả sử \(A\left( {a\,;\,\,3 - a} \right)\); \(B\left( {2b + 6\,;\,\,b} \right)\).
Ta có \(I\) là trung điểm của đoạn thẳng \[AB\] khi và chỉ khi
\(\left\{ {\begin{array}{*{20}{l}}{\frac{{a + 2b + 6}}{2} = 1}\\{\frac{{3 - a + b}}{2} = - 1}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + 2b = - 4}\\{a - b = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 3}\end{array}} \right.} \right.\).
\( \Rightarrow A\left( {2\,;\,\,1} \right)\,,\,\,B\left( {0\,;\,\, - 3} \right) \Rightarrow \overrightarrow {BA} = \left( {2\,;\,\,4} \right) \Rightarrow \overrightarrow {BA} = 2 \cdot \overrightarrow {{u_1}} .\)
Vậy đường thẳng AB có một vectơ chỉ phương là \(\overrightarrow {{u_1}} = \left( {1\,;\,\,2} \right).\) Chọn A.
Câu 26:
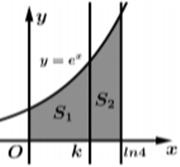
 Xem đáp án
Xem đáp án
Ta có \({S_1} + {S_2} = \int\limits_0^{\ln 4} {{e^x}} \,{\rm{d}}x = \left. {{e^x}} \right|_0^{\ln 4} = 4 - 1 = 3.\)
Mà \({S_1} = 2{S_2}\) nên \(2{S_2} + {S_2} = 3 \Leftrightarrow {S_2} = 1.\)
Do đó \({S_2} = \int\limits_0^{\ln 4} {{e^x}} \,{\rm{d}}x = 1 \Leftrightarrow 4 - {e^k} = 1 \Leftrightarrow {e^k} = 3 \Leftrightarrow k = \ln 3.\) Chọn C.Câu 27:
Cho \({4^x} + {4^{ - x}} = 7.\) Khi đó biểu thức \(P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + 4 \cdot {2^x} + 4 \cdot {2^{ - x}}}} = \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản và \(a,\,b \in \mathbb{Z}.\) Giá trị của \[ab\] bằng
 Xem đáp án
Xem đáp án
Ta có \({4^x} + {4^{ - x}} = 7 \Leftrightarrow {\left( {{2^x}} \right)^2} + 2 \cdot {2^x} \cdot {2^{ - x}} + {\left( {{2^{ - x}}} \right)^2} - 2 = 7\)
\( \Leftrightarrow {\left( {{2^x} + {2^{ - x}}} \right)^2} = 9 \Leftrightarrow {2^x} + {2^{ - x}} = 3.{\rm{ }}\)
Do đó \(P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + 4 \cdot {2^x} + 4 \cdot {2^{ - x}}}} = \frac{{5 - \left( {{2^x} + {2^{ - x}}} \right)}}{{8 + 4 \cdot \left( {{2^x} + {2^{ - x}}} \right)}} = \frac{{5 - 3}}{{8 + 4 \cdot 3}} = \frac{1}{{10}}\).
Suy ra \(a = 1,\,\,b = 10.\) Do đó \(ab = 10.\) Chọn A.
Câu 28:
Trong không gian \[Oxyz,\] có bao nhiêu giá trị nguyên của tham số \(m\) để \({x^2} + {y^2} + {z^2} + 2\left( {m + 2} \right)x - 2\left( {m - 1} \right)z + 3{m^2} - 5 = 0\) là một phương trình một mặt cầu?
 Xem đáp án
Xem đáp án
Phương trình đã cho là phương trình mặt cầu khi và chỉ khi
\[{\left( {m + 2} \right)^2} + {\left( {m + 1} \right)^2} - 3{m^2} + 5 > 0\]\( \Leftrightarrow {m^2} - 2m - 10 < 0\)\( \Leftrightarrow - 1 - \sqrt {11} < m < 1 + \sqrt {11} \).
Theo bài ra \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4} \right\}\).
Vậy có 7 giá trị nguyên của \(m\) thỏa mãn bài toán. Chọn D.
Câu 29:
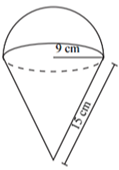
 Xem đáp án
Xem đáp án
Que kem được chia làm hai phần, phần trên là nửa hình cầu, phần dưới là hình nón.
Thể tích phần trên là: \({V_c} = \frac{1}{2} \cdot \frac{4}{3}\pi {r^3} = \frac{2}{3} \cdot {9^3}\pi = 486\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Chiều cao hình nón là: \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{15}^2} - {9^2}} = 12.\)
Thể tích hình nón là: \({V_n} = \frac{1}{3} \cdot h \cdot {r^2}\pi = \frac{1}{3} \cdot 12 \cdot {9^2}\pi = 324\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Vậy thể tích que kem là: \(V = {V_n} + {V_c} = 810\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn B.
Câu 30:
Cho số phức thỏa mãn \(\left| {z - 1 + 2i} \right| = 3.\) Biết rằng tập hợp các điểm biểu diễn của số phức \(w = 2z + i\) trên mặt phẳng tọa độ \[Oxy\] là một đường tròn. Tâm của đường tròn đó là
 Xem đáp án
Xem đáp án
Gọi \(M\) là điểm biểu diễn số phức \[w.\] Ta có \(w = 2z + i \Leftrightarrow z = \frac{{w - i}}{2}.\)
Do đó tập hợp điểm \(M\) là đường tròn tâm \(I\left( {2\,;\,\, - 3} \right)\) và bán kính \(R = 6.\) Chọn A.
Câu 31:
Có bao nhiêu số thực dương \(a\) để tích phân \(\int\limits_0^1 {\frac{{2x + a}}{{x + a}}} \;{\rm{d}}x = 2 - 2a\)?
 Xem đáp án
Xem đáp án
Ta có \[\int\limits_0^1 {\frac{{2x + a}}{{x + a}}} \;{\rm{d}}x = \int\limits_0^1 {\frac{{2\left( {x + a} \right) - a}}{{x + a}}} \;{\rm{d}}x = \int\limits_0^1 {\left( {2 - \frac{a}{{x + a}}} \right)} \;{\rm{d}}x\]
\( = \left. {\left( {2x - a\ln \left| {x + a} \right|} \right)} \right|_0^1 = 2 - a \cdot \ln \left| {a + 1} \right| + a \cdot \ln \left| a \right|\)\( = 2 - a \cdot \left[ {\ln \left( {a + 1} \right) - \ln a} \right] = 2 - a \cdot \ln \left( {\frac{{a + 1}}{a}} \right)\)
Theo bài ra, ta được \(2 - a \cdot \ln \left( {\frac{{a + 1}}{a}} \right) = 2 - 2a\)
\( \Leftrightarrow \ln \left( {\frac{{a + 1}}{a}} \right) = 2 \Leftrightarrow \frac{{a + 1}}{a} = {e^2} \Leftrightarrow a = \frac{1}{{{e^2} - 1}}.\) Chọn C.
Câu 32:
Một lớp học gồm 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Lý và 5 học sinh giỏi cả Toán và Lý. Chọn ngẫu nhiên một học sinh, xác suất để học sinh đó giỏi Toán hoặc giỏi Lý là
 Xem đáp án
Xem đáp án
Gọi \[A\] là biến cố học sinh giỏi toán, \[B\] là biến cố học sinh giỏi lý.
Ta có \(AB\) là biến cố học sinh giỏi toán và lý.
\(A \cup B\) là biến cố học sinh giỏi toán hoặc lý.
Khi đó \(P\left( A \right) = \frac{{15}}{{40}} = \frac{3}{8}\,;\,\,P\left( B \right) = \frac{{10}}{{40}} = \frac{1}{4}\,;\,\,P\left( {AB} \right) = \frac{5}{{40}} = \frac{1}{8}.\)
Do đó \[P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{3}{8} + \frac{1}{4} - \frac{1}{8} = \frac{4}{8} = \frac{1}{2}.\] Chọn B.
Câu 33:
Cho tứ diện \[ABCD\]. Gọi \[M,\,\,N,\,\,E\] lần lượt là trung điểm của \[AB,\,\,BD,\,\,DA.\] Tỉ số thể tích của hai khối tứ diện \[MNEC\] và \[ABCD\] bằng
 Xem đáp án
Xem đáp án
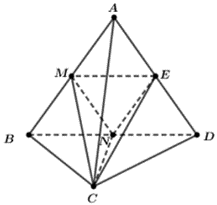
Ta có \({V_{ABCD}} = {V_{C.ABD}} = \frac{1}{3}{S_{ABD}} \cdot d\left( {C,\,\,\left( {ABD} \right)} \right)\);
\({V_{MNEC}} = {V_{C.MNE}} = \frac{1}{3}{S_{MNE}} \cdot d\left( {C,\,\,\left( {MNE} \right)} \right) = \frac{1}{3}{S_{MNE}} \cdot d\left( {C,\,\,\left( {ABD} \right)} \right);\)
\(\frac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \frac{{\frac{1}{3}{S_{MNE}} \cdot d\left( {C,\,\,\left( {ABD} \right)} \right)}}{{\frac{1}{3}{S_{ABD}} \cdot d\left( {C,\,\,\left( {ABD} \right)} \right)}} = \frac{{{S_{MNE}}}}{{{S_{ABD}}}}.\)Dễ thấy theo tỉ số \[\frac{1}{2}\] nên \(\frac{{{S_{MNE}}}}{{{S_{ABD}}}} = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4}.\)
Do đó \(\frac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \frac{{{S_{MNE}}}}{{{S_{ABD}}}} = \frac{1}{4}.\) Chọn B.
Câu 34:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) sao cho Xét hàm số \(g\left( x \right) = f\left( {{x^3} + x} \right) - {x^2} + 2x + m.\) Giá trị của tham số \(m\) để \[{\max _{x \in \left[ {0\,;\,\,2} \right]}}g\left( x \right) = 8\] là\({\max _{x \in \left[ {0\,;\,\,10} \right]}}f\left( x \right) = f\left( 2 \right) = 4.\)
 Xem đáp án
Xem đáp án
Đặt \(t = {x^3} + x.\) Vì \(x \in \left[ {0\,;\,\,2} \right]\) nên \(t \in \left[ {0\,;\,\,10} \right].\)
Ta có: \({\max _{x \in \left[ {0\,;\,\,2} \right]}}g\left( x \right) = {\max _{x \in \left[ {0\,;\,\,2} \right]}}\left[ {f\left( {{x^3} + x} \right) - {x^2} + 2x + m} \right]\)
\( = {\max _{x \in \left[ {0\,;\,\,2} \right]}}f\left( {{x^3} + x} \right) + {\max _{x \in \left[ {0\,;\,\,2} \right]}}\left( { - {x^2} + 2x + m} \right)\)
\( = {\max _{x \in \left[ {0\,;\,\,10} \right]}}f\left( t \right) + 1 + m\) (với \(t = {x^3} + x\) và \({\max _{x \in \left[ {0\,;\,\,2} \right]}}\left[ { - {x^2} + 2x + m} \right] = 1 + m\)).
\( = {\max _{x \in \left[ {0\,;\,\,10} \right]}}f\left( x \right) + 1 + m = 4 + 1 + m = 5 + m.\)
Suy ra \({\max _{x \in \left[ {0\,;\,\,2} \right]}}g(x) = 5 + m \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{t = 2}\end{array} \Leftrightarrow x = 1} \right..\)
Theo giả thiết, ta có: \({\max _{x \in \left[ {0\,;\,\,2} \right]}}g\left( x \right) = 8 \Leftrightarrow m + 5 = 8 \Leftrightarrow m = 3.\) Chọn D.
Câu 35:
Trong không gian \[Oxyz,\] cho đường thẳng \(\Delta :\frac{{x - 1}}{2} = \frac{y}{2} = \frac{{z + 2}}{{ - 1}}\) và hai điểm \(A\left( {0\,;\,\, - 1\,;\,\,3} \right),\) \(B\left( {1\,;\,\, - 2\,;\,\,1} \right).\) Điểm \(M\) thuộc đường thẳng \(\Delta \) sao cho \(M{A^2} + 2M{B^2}\) đạt giá trị nhỏ nhất. Khi đó, tọa độ là
 Xem đáp án
Xem đáp án
Ta có \(M \in \Delta \Rightarrow M\left( {1 + 2t\,;\,\,t\,;\,\, - 2 - t} \right)\) nên ta có
• \(M{A^2} = {\left( { - 1 - 2t} \right)^2} + {\left( { - 1 - t} \right)^2} + {\left( {5 + t} \right)^2} = 6{t^2} + 16t + 27\);
• \(M{B^2} = {\left( { - 2t} \right)^2} + {\left( { - 2 - t} \right)^2} + {\left( {3 + t} \right)^2} = 6t + 10t + 13\).
Suy ra \(M{A^2} + 2M{B^2} = 18{t^2} + 36t + 53 = 18\left( {{t^2} + 2t + 1} \right) + 35\)\( = 18{(t + 1)^2} + 35 \ge 35\).
Do đó \(M{A^2} + 2M{B^2}\) đạt giá trị nhỏ nhất khi \(t = - 1\).
Vậy \(M\left( { - 1\,;\,\, - 1\,;\,\, - 1} \right).\) Chọn C.
Câu 36:
Cho các tập hợp khác rỗng \(A = \left[ {2m\,;\,\,m + 3} \right]\) và \(B = \left( { - \infty \,;\,\, - 2} \right] \cup \left( {4\,;\,\, + \infty } \right).\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để \(A \cap B \ne \emptyset \)?
 Xem đáp án
Xem đáp án
Các giá trị nguyên dương của tham số \(m\) để \(A \cap B \ne \emptyset \) là \[m \in \left\{ {2\,;\,\,3} \right\}\].
Do đó có 2 giá trị nguyên dương yêu cầu bài toán.
Đáp án: 2.
Câu 37:
 Xem đáp án
Xem đáp án
Từ 1 đến 20 có 10 số chẵn và 10 số lẻ, trong 10 số chẵn thì có 5 số chia hết cho 4.
• Chọn 3 quả số lẻ có \(C_{10}^3\) (cách).
• Chọn 1 quả số chẵn chia hết cho 4 có \(C_5^1\) (cách).
• Chọn 1 quả số chẵn không chia hết cho 4 có \(C_5^1\) (cách).
Suy ra có \(C_{10}^3.\) \(C_5^1.\) \(C_5^1 = 3\,\,000\) (cách).
Đáp án: 3000.
Câu 38:
 Xem đáp án
Xem đáp án
Xét \(t = 2{x^3} - 3{x^2} + m \Rightarrow t = 6{x^2} - 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\end{array}} \right..\)
Do đó \({\min _{\left[ { - 1\,;\,\,3} \right]}}t\left( x \right) = m - 5\,;\,\,{\max _{\left[ { - 1\,;\,\,3} \right]}}t\left( x \right) = m + 27.\)
• Nếu \[m - 5 \ge 0 \Rightarrow {\min _{\left[ { - 1\,;\,\,3} \right]}}f\left( x \right) = m - 5 \le 3 \Leftrightarrow 5 \le m \le 8 \Rightarrow m \in \left\{ {5\,;\,\,6\,;\,\,7\,;\,\,8} \right\}.\]
• Nếu \(m + 27 \le 0 \Rightarrow {\min _{\left[ { - 1\,;\,\,3} \right]}}f\left( x \right) = - \left( {m + 27} \right) \le 3 \Leftrightarrow - 30 \le m \le - 27\)
\( \Rightarrow m \in \left\{ { - 30\,;\,\, - 29\,;\,\, - 28\,;\,\, - 27} \right\}.\)
• Nếu \[\left( {m - 5} \right)\left( {m + 27} \right) \le 0 \Rightarrow {\min _{\left[ { - 1\,;\,\,3} \right]}}f\left( x \right) = 0.\]
Vậy \[m \in \left\{ { - 30\,;\,\, - 29\,;\,\, - 28\,;\,\, \ldots ;\,\,8} \right\}\] có tất cả 39 số nguyên thỏa mãn.
Đáp án: 39.
Câu 39:
Một quả bóng được ném lên theo phương thẳng đứng từ mặt đất với vận tốc ban đầu \(19,6\;\,{\rm{m}}/{\rm{s}}.\) Khi bỏ qua sức cản của không khí, độ cao của quả bóng so với mặt đất (tính bằng mét) được mô tả bởi phương trình \(h(t) = - 4,9{t^2} + 19,6t\) với \(t\) tính bằng giây. Độ cao lớn nhất của quả bóng bằng bao nhiêu mét? (kết quả làm tròn đến hàng đơn vị).
 Xem đáp án
Xem đáp án
Phương trình vận tốc của quả bóng là \(v(t) = h'(t) = - 9,8t + 19,6\,\,(\;{\rm{m}}/{\rm{s}})\).
Độ cao lớn nhất quả bóng đạt được khi \(v(t) = 0 \Leftrightarrow - 9,8t + 19,6 = 0 \Leftrightarrow t = 2.\)
Khi đó \(h\left( 2 \right) = - 4,9 \cdot {2^2} + 19,6 \cdot 2 = 19,6\,\,(m).\)
Đáp án: \[{\bf{19}},{\bf{6}}\].
Câu 40:
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{2{\rm{x}} + 2{\rm{ khi x}} \ge 1}\\{3{{\rm{x}}^2} + 1{\rm{ khi }}x < 1}\end{array}} \right..\) Giả sử \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) thoả mãn \(F\left( 0 \right) = 2.\) Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng
 Xem đáp án
Xem đáp án
Ta có \(F\left( x \right) = \int f \left( x \right){\rm{d}}x = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + {C_1}}&{{\rm{ khi }}x \ge 1}\\{{x^3} + x + {C_2}}&{{\rm{ khi }}x < 1}\end{array}} \right.\).
Theo bài ra, ta có \(F\left( 0 \right) = 2 \Rightarrow {C_2} = 2\).
Hàm số \(F\left( x \right)\) liên tục nên \(\mathop {\lim }\limits_{x \to {1^ + }} F\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} F\left( x \right)\)
\[ \Leftrightarrow 3 + {C_1} = 4 \Leftrightarrow {C_1} = 1 \Rightarrow F\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{{x^2} + 2x + 1{\rm{ khi }}x \ge 1}\\{{x^3} + x + 2{\rm{ }}\,\,{\rm{khi }}x < 1}\end{array}} \right.\].
Vậy \(F\left( { - 1} \right) + 2F\left( 2 \right) = {\left( { - 1} \right)^3} + \left( { - 1} \right) + 2 + 2 \cdot \left( {{2^2} + 2 \cdot 2 + 1} \right) = 18.\)
Đáp án: 18.
Câu 41:
Biết rằng đồ thị của hàm số \(y = \frac{{\left( {n - 3} \right)x + n - 2017}}{{x + m + 3}}\) (\[m,\,\,n\] là tham số thực) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cận đứng. Tính \[m + n.\]
 Xem đáp án
Xem đáp án
Theo công thức tìm nhanh tiệm cận của đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\) ta có:
• Đồ thị hàm số nhận \(x = - \frac{d}{c} = - m - 3 = 0\) làm TCĐ \( \Rightarrow m = - 3.\)
• Đồ thị hàm số nhận \(y = {\frac{a}{c}^c} = n - 3 = 0\) làm \({\rm{TCN}} \Rightarrow n = 3.\)
Vậy \(m + n = 0.\) Đáp án: 0.
Câu 42:
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\left( {0\,;\,\, + \infty } \right)\) thỏa mãn \(f\left( 1 \right) = \frac{1}{3}\) và \(3x \cdot f\left( x \right) - {x^2} \cdot f'\left( x \right) = 2{f^2}\left( x \right)\), với \(f\left( x \right) \ne 0,\,\,\forall x \in \left( {0\,;\,\, + \infty } \right).\) Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \[\left[ {1\,;\,\,2} \right].\] Tính \(M + m.\)
 Xem đáp án
Xem đáp án
Ta có: \(3x \cdot f\left( x \right) - {x^2} \cdot f'\left( x \right) = 2{f^2}\left( x \right)\)\( \Leftrightarrow 3{x^2} \cdot f\left( x \right) - {x^3} \cdot f'\left( x \right) = 2x \cdot {f^2}\left( x \right)\)
\( \Leftrightarrow \frac{{3{x^2}f\left( x \right) - {x^3}f'\left( x \right)}}{{{f^2}\left( x \right)}} = 2x \Leftrightarrow {\left( {\frac{{{x^3}}}{{f\left( x \right)}}} \right)^\prime } = 2x\).
Khi đó \(\int {{{\left( {\frac{{{x^3}}}{{f\left( x \right)}}} \right)}^\prime }} {\rm{d}}x = \int 2 x\;{\rm{d}}x \Leftrightarrow \frac{{{x^3}}}{{f\left( x \right)}} = {x^2} + C\).
Do \(f\left( 1 \right) = \frac{1}{3} \Rightarrow \frac{1}{{1 + C}} = \frac{1}{3} \Rightarrow C = 2.\) Do đó \(f\left( x \right) = \frac{{{x^3}}}{{{x^2} + 2}}\).
Tìm được \(M = f\left( 2 \right) = \frac{4}{3},\,\,m = f\left( 1 \right) = \frac{1}{3} \Rightarrow M + m = \frac{5}{3}.\)
Đáp án: \(\frac{5}{3}.\)
Câu 43:
Trong không gian \[Oxyz,\] cho ba đường thẳng có phương trình lần lượt là \(d:\frac{x}{1} = \frac{y}{2} = \frac{{z + 1}}{{ - 2}},\) \({\Delta _1}:\frac{{x - 3}}{2} = \frac{y}{1} = \frac{{z - 1}}{1}\) và \({\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{z}{1}.\) Đường thẳng \(\Delta \) vuông góc với \(d\) đồng thời cắt \({\Delta _1},\,\,{\Delta _2}\) tương ứng tại \[H,\,\,K\] sao cho độ dài \[HK\] nhỏ nhất. Biết rằng \(\Delta \) có một vectơ chỉ phương \(\vec u\left( {h\,;\,\,k\,;\,\,1} \right).\) Giá trị \(h - k\) bằng
 Xem đáp án
Xem đáp án
Ta có \(H \in {\Delta _1} \Leftrightarrow H\left( {3 + 2t\,;\,\,t\,;\,\,1 + t} \right)\) và \(K \in {\Delta _2} \Leftrightarrow K\left( {1 + m\,;\,\,2 + 2m\,;\,\,m} \right).\)
Suy ra \(\overrightarrow {HK} = \left( {m - 2t - 2\,;\,\,2m - t + 2\,;\,\,m - t - 1} \right).\)
Đường thẳng \(d\) có một VTCP là \(\overrightarrow {{u_d}} = \left( {1\,;\,\,1\,;\,\, - 2} \right).\)
\(\Delta \bot d \Leftrightarrow \overrightarrow {{u_d}} \cdot \overrightarrow {HK} = 0 \Leftrightarrow m - t + 2 = 0 \Leftrightarrow m = t - 2 \Rightarrow \overrightarrow {HK} = \left( { - t - 4\,;\,\,t - 2\,;\,\, - 3} \right){\rm{. }}\)
Ta có \(H{K^2} = {\left( { - t - 4} \right)^2} + {\left( {t - 2} \right)^2} + {\left( { - 3} \right)^2} = 2{\left( {t + 1} \right)^2} + 27 \ge 27\,,\,\,\forall t \in \mathbb{R}\).
Khi đó ta có \(H{K_{\min }} = \sqrt {27} \), đạt được khi \(t = - 1.\)
Do đó \(\overrightarrow {HK} = \left( { - 3\,;\,\, - 3\,;\,\, - 3} \right)\), suy ra \(\vec u\left( {1\,;\,\,1\,;\,\,1} \right) \Rightarrow h = k = 1 \Rightarrow h - k = 0.\)
Đáp án: 0.
Câu 44:
Có bao nhiêu giá trị nguyên của tham số \[m \in \left( { - 20;\,\, + \infty } \right)\] để bất phương trình \({4^{{x^2}}} - \left( {m + 1} \right){2^{{x^2} + 1}} + m + 3 \ge 0\) nghiệm đúng với mọi \(x \in \mathbb{R}\)?
 Xem đáp án
Xem đáp án
Tập xác định \(D = \mathbb{R}.\)
Đặt \(t = {2^{{x^2}}}\,\,\left( {t \ge 1} \right)\), khi đó bất phương trình trở thành \({t^2} - 2\left( {m + 1} \right)t + m + 3 \ge 0\)
Với \(t \ge 1\) thì \((*) \Leftrightarrow {t^2} - 2t + 3 \ge m\left( {2t - 1} \right) \Leftrightarrow \frac{{{t^2} - 2t + 3}}{{2t - 1}} \ge m.\)
Xét hàm số \(f\left( t \right) = \frac{{{t^2} - 2t + 3}}{{2t - 1}}\) trên \(\left[ {1\,;\,\, + \infty } \right)\).
Ta có \(f'\left( t \right) = \frac{{\left( {2t - 2} \right)\left( {2t - 1} \right) - 2\left( {{t^2} - 2t + 3} \right)}}{{{{\left( {2t - 1} \right)}^2}}} = \frac{{2{t^2} - 2t - 4}}{{{{\left( {2t - 1} \right)}^2}}}.\)
Do đó hàm số \(f\left( t \right)\) có bảng biến thiên như sau:
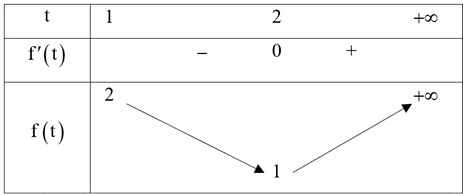
Dựa vào bảng biến thiên ta thấy để bất phương trình \(f\left( t \right) \ge m,\,\,\forall t \in \left[ {1\,;\,\, + \infty } \right)\) thì \(m \le 1.\)
Vậy có 21 giá trị nguyên \(m\) thỏa mãn yêu cầu bài toán.
Đáp án: 21.
Câu 45:
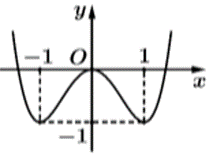
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ bên. Phương trình \[\sqrt {f\left( {\sqrt {f\left( x \right)} } \right) + 2} = f\left( x \right) + 1\] có bao nhiêu nghiệm thực phân biệt?
 Xem đáp án
Xem đáp án
Dựa vào hình vẽ, ta có \(f\left( x \right) = {x^4} - 2{x^2}.\)
Suy ra \(f\left( u \right) = {u^4} - 2{u^2}.\)
Đặt \(u = \sqrt {f\left( x \right)} \ge 0\), phương trình trở thành \(\sqrt {f\left( u \right) + 2} = {u^2} + 1\)
\( \Leftrightarrow f\left( u \right) + 2 = {\left( {{u^2} + 1} \right)^2}\)\( \Leftrightarrow {u^4} - 2{u^2} + 2 = {u^4} + 2{u^2} + 1\)\( \Leftrightarrow {u^2} = \frac{1}{4} \Leftrightarrow f\left( x \right) = \frac{1}{4}\).
Dựa vào hình vẽ, ta thấy đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = \frac{1}{4}\) tại 2 điểm phân biệt nên phương trình đã cho có 2 nghiệm thực phân biệt.
Đáp án: 2.
Câu 46:
Trong không gian \[Oxyz,\] cho hai đường thẳng \({d_1}:\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = - 3}\\{z = 2 - 2t}\end{array}} \right.\) và \({d_2}:\frac{{x + 3}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z + 4}}{3}.\) Phương trình mặt phằng \((P)\) cách đều hai đường thẳng \({d_1}\) và \({d_2}\) có dạng \(ax + by + cz + 11 = 0.\) Giá trị của \(a + 2b + 3c\) bằng
 Xem đáp án
Xem đáp án
Đường thẳng \({d_2}\) có vectơ chỉ phương \[\vec v = \left( {1\,;\,\, - 2\,;\,\,3} \right)\] và đi qua điểm \(N\left( { - 3\,;\,\,1\,;\,\, - 4} \right).\)
Ta có: \(\left[ {\vec v\,,\,\,\vec u} \right] = \left( {4\,;\,\,5\,;\,\,2} \right) \ne \vec 0\,;\,\,\overrightarrow {MN} = \left( { - 4\,;\,\,4\,;\,\, - 6} \right)\,;\,\,\left[ {\vec v\,,\,\,\vec u} \right] \cdot \overrightarrow {MN} = - 16 + 20 - 12 = - 8 \ne 0\)
\( \Rightarrow {d_1}\) và \({d_2}\) chéo nhau.
Mặt phẳng \((P)\) cách đều hai đường thẳng \({d_1}\) và \({d_2}\) nên \((P)\) nhận \(\left[ {\vec v\,,\,\,\vec u} \right] = \left( {4\,;\,\,5\,;\,\,2} \right)\) là vectơ pháp tuyến và đi qua trung điểm \(I\left( { - 1\,;\,\, - 1\,;\,\, - 1} \right)\) của đoạn MN
Suy ra phương trình của \((P):4\left( {x + 1} \right) + 5\left( {y + 1} \right) + 2\left( {z + 1} \right) = 0 \Leftrightarrow 4x + 5y + 2z + 11 = 0\)
\( \Rightarrow a = 4\,;\,\,b = 5\,;\,\,c = 2 \Rightarrow a + 2b + 3c = 20.\)
Đáp án: 20.
Câu 47:
Trong các số phức \(z\) thỏa mãn điều kiện \(\left| {z - 2 - 4i} \right| = \left| {z - 2i} \right|.\) Biết rằng số phức \(z = x + yi\,\,\left( {x,\,y \in \mathbb{R}} \right)\) có môđun nhỏ nhất. Tính \(P = {x^2} + {y^2}.\)
 Xem đáp án
Xem đáp án
Gọi \(z = x + yi\,\,\left( {x,\,y \in \mathbb{R}} \right).\)
Ta có \(\left| {z - 2 - 4i} \right| = \left| {z - 2i} \right| \Leftrightarrow \left| {\left( {x - 2} \right) + \left( {y - 4} \right)i} \right| = \left| {x + \left( {y - 2} \right)i} \right|\)
\( \Leftrightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 4} \right)}^2}} = \sqrt {{x^2} + {{\left( {y - 2} \right)}^2}} \)
\( \Leftrightarrow {x^2} - 4x + 4 + {y^2} - 8y + 16 = {x^2} + {y^2} - 4y + 4\)
\( \Leftrightarrow 4x + 4y - 16 = 0 \Leftrightarrow y = 4 - x{\rm{. }}\)
Do đó \(\left| z \right| = \sqrt {{x^2} + {y^2}} = \sqrt {{x^2} + {{\left( {4 - x} \right)}^2}} = \sqrt {2{x^2} - 8x + 16} = \sqrt {2{{\left( {x - 2} \right)}^2} + 8} \ge 2\sqrt 2 .\)
Dấu" =" xảy ra \( \Leftrightarrow x = 2 \Rightarrow y = 2.\) Vậy \(P = {2^2} + {2^2} = 8.\)
Đáp án: 8.
Câu 48:
Xét các số thực dương \[x,\,\,y\] thỏa mãn \(\frac{1}{2}{\log _2}\frac{x}{4} + {\log _2}y = \frac{{4 - x{y^2}}}{{{y^2}}}.\) Khi \(x + 4y\) đạt giá trị nhỏ nhất thì giá trị \(\frac{x}{y}\) bằng
 Xem đáp án
Xem đáp án
Giải thiết trở thành: \({\log _2}x - {\log _2}4 + 2{\log _2}y = \frac{8}{{{y^2}}} - 2x\)
\( \Leftrightarrow {\log _2}x - {\log _2}4 - {\log _2}{y^{ - 2}} = 8 \cdot {y^{ - 2}} - 2x\)
\( \Leftrightarrow {\log _2}x + 2x = {\log _2}4 + {\log _2}{y^{ - 2}} + 2 \cdot \left( {4 \cdot {y^{ - 2}}} \right)\)
\( \Leftrightarrow {\log _2}x + 2x = {\log _2}\left( {4{y^{ - 2}}} \right) + 2 \cdot \left( {4{y^{ - 2}}} \right)\)
Xét hàm số \(f\left( t \right) = {\log _2}t + 2t\,\,\left( {t > 0} \right)\) có \(f'\left( t \right) = \frac{1}{{t\ln 2}} + 2 > 0,\,\,\forall t > 0\)
Suy ra hàm số \(f(t)\) đồng biến trên khoảng \((0; + \infty ).\)
Do đó \[f\left( x \right) = f\left( {4{y^{ - 2}}} \right) \Leftrightarrow x = 4{y^{ - 2}} \Leftrightarrow x = \frac{4}{{{y^2}}}\].
Đặt \(P = x + 4y = 2y + 2y + \frac{4}{{{y^2}}} \ge 3\sqrt[3]{{2y \cdot 2y \cdot \frac{4}{{{y^2}}}}} = 6\sqrt[3]{2}.\)
Dấu "=" xảy ra khi \(2y = \frac{4}{{{y^2}}} \Leftrightarrow y = \sqrt[3]{2} \Rightarrow \frac{x}{y} = \frac{4}{{{y^3}}} = \frac{4}{2} = 2.\)
Đáp án: 2.
Câu 49:
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau. Gọi \[M,\,\,N\] lần lượt là hai điểm thuộc \(A'C\) và \(BC'\) sao cho \[MN\] là đoạn vuông góc chung của hai đường thẳng đó. Tính tỉ số \(\frac{{NB}}{{NC'}}.\)
 Xem đáp án
Xem đáp án
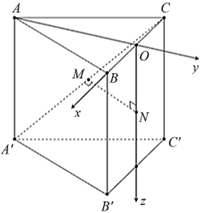
Kết quả bài toán sẽ không thay đổi nếu ta xét lăng trụ đều \(ABC.A'B'C'\) có cạnh bên bằng cạnh đáy bằng 2.
Chọn hệ trục tọa độ \[Oxyz\] như hình vẽ \(O\) là trung điểm của \(BC).\)
Ta có \(A'\left( {0\,;\,\, - \sqrt 3 \,;\,\,2} \right),\,\,B\left( {1\,;\,\,0\,;\,\,0} \right),\,\,C\left( { - 1\,;\,\,0;0} \right),\,\,C'\left( { - 1\,;\,\,0\,;\,\,2} \right)\)
Suy ra \(\overrightarrow {CA'} = \left( {1\,;\,\, - \sqrt 3 \,;\,\,2} \right),\overrightarrow {BC'} = \left( { - 2\,;\,\,0\,;\,\,2} \right).\)Do \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {CM} = m\overrightarrow {CA'} }\\{\overrightarrow {BN} = n\overrightarrow {BC'} }\end{array}} \right.\) nên ta có \(M\left( { - 1 + m\,;\,\, - \sqrt 3 m\,;\,\,2m} \right),N\left( {1 - 2n\,;\,\,0\,;\,\,2n} \right).\)
Suy ra \(\overrightarrow {MN} = \left( { - m - 2n + 2\,;\,\,\sqrt 3 m\,;\,\,2n - 2m} \right).\)
Đường thẳng \[MN\] là đường vuông góc chung của \(A'C\) và \(BC'\) nên
\(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {MN} \cdot \overrightarrow {CA'} = 0}\\{\overrightarrow {MN} \cdot \overrightarrow {BC'} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 4m + 2n = - 1}\\{ - m + 4n = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m = \frac{2}{5}}\\{n = \frac{3}{5}}\end{array}} \right.} \right.} \right.\)\( \Rightarrow \frac{{BN}}{{BC'}} = n = \frac{3}{5} \Rightarrow \frac{{NB}}{{NC'}} = \frac{3}{2}.\)
Đáp án: \[{\bf{1}},{\bf{5}}\].
Câu 50:
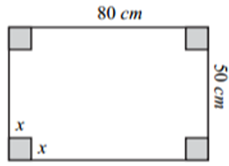
 Xem đáp án
Xem đáp án
Điều kiện: \(0 < x < 50.\) Chiều dài hình hộp là: \(80 - x\,\,(\;{\rm{cm}})\).
Chiều rộng hình hộp là: \(50 - x\,\,(\;{\rm{cm}})\); Chiều cao hình hộp là: \(x\,\,(\;{\rm{cm}})\).
Thể tích hình hộp là: \(V = x\left( {80 - x} \right)\left( {50 - x} \right)\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Ta có \(V' = 3{x^2} - 260x + 4000\,;\,\,V' = 0 \Leftrightarrow x = 20\,\,\left( {0 < x < 50} \right).\)
Ta có bảng biến thiên:
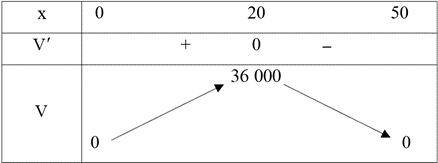
Như vậy, \({V_{\max }} = 36\,\,000\,\;{\rm{c}}{{\rm{m}}^3}.\)
Đáp án: \[{\bf{36}}\,\,{\bf{000}}\].
Câu 51:
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Cảm xúc bao trùm toàn bộ đoạn thơ là nỗi nhớ được thể hiện qua điệp từ “nhớ” được lặp lại nhiều lần trong đoạn thơ. Chọn A.
Câu 52:
 Xem đáp án
Xem đáp án
Nhân hóa (rừng che bộ đội/ vây quân thù). Chọn B.
Câu 53:
 Xem đáp án
Xem đáp án
Cảm hứng chủ đạo của đoạn thơ là thể hiện khí thế đánh giặc hào hùng của quân và dân ta, đó là biểu hiện của tính sử thi. Chọn C.
Câu 54:
 Xem đáp án
Xem đáp án
Đại từ “ta” là chỉ người dân Việt Bắc và bộ đội, chiến sĩ kháng chiến đã cùng nhau chung sức đồng lòng đánh Tây. Chọn D.
Câu 55:
 Xem đáp án
Xem đáp án
Đoạn thơ tái hiện lại chân thực khung cảnh thiên nhiên cùng đất trời Việt Bắc trong cuộc chiến đánh giặc. Chọn A.
Câu 56:
 Xem đáp án
Xem đáp án
Nội dung chính của đoạn trích là: Cuộc sống tại nhà thống lí Pá Tra rút cạn sức sống của Mị, Mị chẳng màng đến cái chết. Chọn B.
Câu 57:
 Xem đáp án
Xem đáp án
Thái độ của tác giả dành cho nhân vật Mị là nỗi xót xa cùng cực. Thân phận của Mị từ hồi về nhà thống lí Pá Tra làm dâu gạt nợ chẳng khác nào thân phận “trâu ngựa”. Chọn A.
Câu 58:
 Xem đáp án
Xem đáp án
“Lần lần, mấy năm qua, mấy năm sau, bố Mị chết” các từ in đậm nhằm chỉ khoảng thời gian kéo dài triền miên, từ năm này qua năm khác mà Mị đã phải sống và làm việc cực khổ tại nhà thống lí Pá Tra. Chọn A.
Câu 59:
 Xem đáp án
Xem đáp án
Dựa vào nội dung: Bây giờ thì Mị tưởng mình cũng là con trâu, mình cũng là con ngựa, là con ngựa phải đổi ở cái tàu ngựa nhà này đến ở cái tàu ngựa nhà khác, ngựa chỉ biết việc ăn cỏ, biết đi làm mà thôi. → Mị tự so sánh mình là: Con trâu, con ngựa. Chọn A.
Câu 60:
 Xem đáp án
Xem đáp án
Các từ “hái, bẻ, tước” chỉ hoạt động của tay. Từ “nhai” chỉ hoạt động của miệng. Từ khác các từ còn lại là “nhai”. Chọn D.
Câu 61:
 Xem đáp án
Xem đáp án
Câu (4) không xuất hiện từ so sánh hay đồ vật/con vật → Loại phương án A, C sai. Từ “kiểu thơm” dùng để chỉ những người con gái xinh đẹp, thanh lịch, yêu kiều → Cách nói ẩn dụ. Chọn B.
Câu 62:
 Xem đáp án
Xem đáp án
Đọc và xác định các từ khóa mô tả những người lính Tây Tiến:
+ “Quân xanh màu lá” → Khắc họa ngoại hình của người lính Tây Tiến: da xanh xao do căn bệnh sốt rét rừng hành hạ.
+ “Gửi mộng qua biên giới”, “mơ Hà Nội” → Sự lãng mạn, hào hoa của những người lính.
+ “Đi chẳng tiếc đời xanh” → Sự sẵn sàng hi sinh của những người lính.
+ Câu (5), (7) nói về cái chết của những người lính Tây Tiến.
Loại trừ đáp án:
+ Câu (1), (2) mang hình ảnh tả thực về đoàn binh Tây Tiến → Loại phương án A, C sai.
+ Câu (5) nói về sự hi sinh của những người lính Tây Tiến → Loại phương án B sai.
→ Chọn D.
Câu 63:
 Xem đáp án
Xem đáp án
Xác định ý nghĩa câu nói “Quyết tử cho Tổ quốc quyết sinh”: sự sẵn sàng hi sinh để bảo vệ nền độc lập của Tổ quốc
Đọc lại ngữ liệu và giải nghĩa các câu thơ:
+ Câu (1), (2) miêu tả chân dung người lính Tây Tiến.
+ Câu (3), (4) ca ngợi vẻ đẹp tâm hồn của người lính Tây Tiến.
+ Câu (5), (7) mô tả hiện thực về sự hi sinh của những người lính Tây Tiến.
+ Câu (6) như một lời thề, lời hứa của những người lính khi bước chân vào chiến trường.
+ Câu (8) ca ngợi sự hi sinh của những người lính trong đoàn binh Tây Tiến.
Xác định câu thơ (6): “Chiến trường đi chẳng tiếc đời xanh” thể hiện quyết tâm chiến đấu, sẵn sàng hi sinh tuổi thanh xuân vì độc lập, tự do của dân tộc, tương đồng về nghĩa và dễ gợi liên tưởng đến câu nói “Quyết tử cho Tổ quốc quyết sinh”. Chọn B.
Câu 64:
 Xem đáp án
Xem đáp án
Đọc kĩ đoạn trích và xác định các từ khóa:
+ “Không mọc tóc”: Căn bệnh sốt rét rừng khiến người lính rụng hết tóc → Chất bi.
+ “Dữ oai hùm”: Sự dữ dằn như hổ báo chốn rừng xanh → Chất tráng.
+ “Mồ viễn xứ”, “chẳng tiếc đời xanh”, “Áo bào thay chiếu, anh về đất”, “Sông Mã gầm lên khúc độc hành” → Sự hi sinh anh dũng của người lính Tây Tiến.
→ Các hình ảnh trong bốn câu thơ đầu nói về vẻ đẹp bi tráng của người lính Tây Tiến và các hình ảnh trong 4 câu sau nói về sự hi sinh anh dũng của họ.
→ Xét tổng thể, chủ đề của cả đoạn trích là bức chân dung bị tráng của người lính Tây Tiến và sự hi sinh anh dũng của họ. Chọn C.
Câu 65:
 Xem đáp án
Xem đáp án
Cụm từ “anh về đất” nói về cái chết, sự hi sinh của những người lính Tây Tiến một cách nhẹ nhàng, như thể những người lính trở về với Tổ quốc, quê hương, những gì thương yêu và thân thuộc.
- Từ “áo bào” liền trước đó gợi hình ảnh về những người tráng sĩ hi sinh trên lưng ngựa xưa kia đã thể hiện sự trân trọng với những người lính, đồng thời khẳng định ý nghĩa về cái chết của họ.
→ Như vậy, phương án A đúng nhưng chưa đủ, phương án B, C không thể hiện đúng tác dụng của biện pháp nói giảm trong câu thơ. Chọn D.
Câu 66:
 Xem đáp án
Xem đáp án
Phương thức biểu đạt chính của đoạn văn là nghị luận. Chọn D.
Câu 67:
 Xem đáp án
Xem đáp án
“Mọi thứ bạn chạm tay vào sẽ biến thành vàng”: gợi nhớ tích truyện Vua Midas thích vàng, hàm ý chỉ những việc mà chúng ta làm sẽ đem lại lợi nhuận dễ dàng, giống như vua Midas trong câu chuyện, hễ chạm vào đâu là chỗ đó lập tức biến thành vàng. Chọn B.
Câu 68:
 Xem đáp án
Xem đáp án
“Trạng thái tinh thần” mà tác giả nói tới trong đoạn trích có nghĩa là một mục đích rõ ràng khi bắt đầu khởi nghiệp và làm giàu. Trạng thái tinh thần cũng là những yếu tố thuộc về tâm lí của người khởi nghiệp: xác định các phương thức để đạt mục tiêu, nghị lực vượt qua khó khăn, thử thách để đạt được mục tiêu; tâm thế khởi nghiệp... Chọn C.
Câu 69:
 Xem đáp án
Xem đáp án
Câu 70:
Nêu biện pháp tu từ được sử dụng trong câu: Mọi thứ bạn chạm tay vào sẽ biến thành vàng. Bạn cho rằng không thể được ư? Thế mà đúng như vậy đấy.
 Xem đáp án
Xem đáp án
Biện pháp tu từ chính được thể hiện trong câu là nói quá: Mọi thứ bạn chạm tay vào sẽ biến thành vàng. Chọn B.
Câu 71:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Sau thời kì đổi mới, các nhà văn đã cho ra những tác phẩm văn học phản ánh cuộc sống chân thật hơn.
 Xem đáp án
Xem đáp án
Câu 72:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Thao tác lập luận bình luận là đưa ra ý kiến đánh giá (xác định phải trái, đúng sai, hay dở), nhận xét (trao đổi ý kiến) về một tình hình, một vấn đề.
 Xem đáp án
Xem đáp án
Thao tác lập luận bình luận là đưa ra ý kiến đánh giá (xác định phải trái, đúng sai, hay dở), bàn bạc (trao đổi ý kiến) về một tình hình, một vấn đề. Chọn C.
Câu 73:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Tình huống là một lát cắt của sự sống, là một khoảnh khắc diễn ra có phần bất ngờ nhưng cái quan trọng là sẽ chi phối nhiều điều trong cuộc sống con người.
 Xem đáp án
Xem đáp án
Nội dung câu văn đề cập về tình huống trong thực tế làm nguồn cảm hứng cho các nhà văn, nhà thơ sáng tác. Vì vậy ta cần hiểu về tình huống là gì? Tình huống là toàn thể những sự việc xảy ra tại một nơi, trong một thời gian, buộc người ta cần phải quan tâm, suy nghĩ giải quyết. Từ “khoảnh khắc” dùng để diễn tả khoảng thời gian hết sức ngắn. Nó không phù hợp với nội hàm của tình huống. Hơn nữa, đặt trong tổng thể từ “khoảnh khắc” ở đây dùng không hợp ngữ cảnh. Sửa: “khoảnh khắc” thành “sự kiện” hoặc “vấn đề”. Chọn B.
Câu 74:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Trong sự chuyển mình của Hà Nội, có những cái tưởng được thêm, và thực chất lại là mất đi một cách rất đáng tiếc.
 Xem đáp án
Xem đáp án
Chú ý thông tin các vế đứng trước và sau từ “và” là 2 vế có nội dung đối lập: “tưởng được thêm” và “thực chất lại mất đi” nên quan hệ từ “và” đang dùng sai, cần thay thế bằng từ “nhưng”. Chọn C.
Câu 75:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Văn học Việt Nam từ đầu thế kỉ XX đến Cách mạng tháng Tám năm 1945 có vị trí hết sức quan trọng trong toàn bộ tiến trình văn học: duy trì tinh hoa văn hóa dân tộc và mở ra một thời kì văn học mới - văn học hiện đại.
 Xem đáp án
Xem đáp án
Lỗi về dùng từ chưa phù hợp với nội dung văn bản: “duy trì” là làm cho nó tồn tại ở mức ban đầu, ở tất cả mọi phương diện, điều đó chưa đáp ứng đầy đủ đặc điểm của văn học Việt Nam từ đầu thế kỉ XX đến Cách mạng tháng Tám năm 1945, do đó, có thể thay thế bằng “kế thừa”. Chọn B.
Câu 76:
 Xem đáp án
Xem đáp án
Các từ “đường sá, chợ búa, bếp núc” được cấu tạo bao gồm một thành tố rõ nghĩa (đường, chợ, bếp) tổ hợp với thành tố không rõ nghĩa (sá, búa, núc). Trong hầu hết các trường hợp, những yếu tố không rõ nghĩa này vốn rõ nghĩa nhưng bị bào mòn dần đi ở các mức độ khác nhau. Riêng từ “trường lớp” lại được cấu tạo bởi 2 thành tố rõ nghĩa (trường, lớp). Chọn B.
Câu 77:
 Xem đáp án
Xem đáp án
Các từ “nguy hiểm, nguy hại, nguy cơ” nói đến điều có thể gây ra tai họa trong một thời gian nào đó. Còn từ “nguy kịch” lại chỉ điều hết sức nguy hiểm, đe doạ nghiêm trọng đến sự sống còn (thường nói về bệnh tật). Chọn C.
Câu 78:
 Xem đáp án
Xem đáp án
Tiếng “công” trong các từ “công lí, bất công, công minh” đều mang ý nghĩa là sự không thiên vị, theo đúng lẽ phải, công bằng; “công” trong “công tác” mang ý nghĩa chỉ công việc. Chọn A.
Câu 79:
 Xem đáp án
Xem đáp án
Hồ Xuân Hương là tác giả thuộc văn học trung đại. Những tác giả còn lại đều thuộc phong trào Thơ mới. Chọn D.
Câu 80:
 Xem đáp án
Xem đáp án
Các từ “bồn chồn, nôn nao, bâng khuâng” cùng chỉ trạng thái tâm lí của con người, còn “lao xao” là từ điển tả âm thanh nhỏ hoặc những tiếng động nhỏ đan vào nhau. Vậy từ khác nghĩa ở đây là “lao xao”. Chọn D.
Câu 81:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Tư tưởng tình cảm của nhà văn trong tác phẩm thường không được nói ra bằng lời mà được biểu hiện bằng _______ và _______.
 Xem đáp án
Xem đáp án
Một tác phẩm văn học dùng nguyên liệu là cốt truyện, nhân vật và ngôn từ. Vì vậy, tình cảm của nhà văn được biểu hiện trong tác phẩm bằng hình tượng và ngôn từ. Còn nhân hóa, so sánh, biểu cảm chỉ là những biện pháp nghệ thuật giúp tác phẩm văn học đó trở nên hay hơn, sống động hơn. Chọn C.
Câu 82:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
______ Tiếng Việt của chúng ta đẹp, ______ tâm hồn của người Việt Nam ta rất đẹp, bởi vì đời sống, cuộc đấu tranh của nhân dân ta từ trước tới nay là cao quý, là vĩ đại, nghĩa là rất đẹp.
(Phạm Văn Đồng)
 Xem đáp án
Xem đáp án
Có lẽ Tiếng Việt của chúng ta đẹp, bởi vì tâm hồn của người Việt Nam ta rất đẹp, bởi vì đời sống, cuộc đấu tranh của nhân dân ta từ trước tới nay là cao quý, là vĩ đại, nghĩa là rất đẹp. Chọn B.
Câu 83:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Lao động là _______ thiêng liêng, là nguồn sống, nguồn hạnh phúc của mỗi người.
 Xem đáp án
Xem đáp án
Lao động là nghĩa vụ thiêng liêng, là nguồn sống, nguồn hạnh phúc của mỗi người. Chọn C.
Câu 84:
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
_________ là tác phẩm tự sự dân gian có quy mô lớn, sử dụng ngôn ngữ có vần, nhịp, xây dựng những hình tượng nghệ thuật hoành tráng, hào hùng để kể về một hoặc nhiều biến cố lớn diễn ra trong đời sống cộng đồng của cư dân thời cổ đại.
 Xem đáp án
Xem đáp án
Sử thi là tác phẩm tự sự dân gian có quy mô lớn, sử dụng ngôn ngữ có vần, nhịp, xây dựng những hình tượng nghệ thuật hoành tráng, hào hùng để kể về một hoặc nhiều biến cố lớn diễn ra trong đời sống cộng đồng của cư dân thời cổ đại. Chọn B.
Câu 85:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Người anh hùng Từ Hải là một sáng tạo _________ của Nguyễn Du về phương diện cảm hứng sáng tạo và nghệ thuật miêu tả.
 Xem đáp án
Xem đáp án
Người anh hùng Từ Hải là một sáng tạo đặc sắc của Nguyễn Du về phương diện cảm hứng sáng tạo và nghệ thuật miêu tả. Chọn B.
Câu 86:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Làm sao được tan ra
Thành trăm con sóng nhỏ
Giữa biển lớn tình yêu
Để ngàn năm còn vỗ.
(Sóng – Xuân Quỳnh)
Đoạn thơ trên thể hiện khát vọng gì của nhân vật trữ tình?
 Xem đáp án
Xem đáp án
Khát khao bất tử hóa trong tình yêu nhưng trái tim nhà thơ không vị kỉ, tầm thường, nhỏ nhen cho riêng mình mà thật lớn lao, cao thượng. Nhà thơ đã hòa niềm hạnh phúc của riêng mình trong niềm hạnh phúc của cuộc đời rộng lớn, cái riêng tồn tại trong cái ta chung, bao la, rộng lớn ấy đã trở thành vĩnh cửu. Chọn A.
Câu 87:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Kèn Ta, kèn Tây, kèn Tàu, lần lượt thay nhau mà rộn lên. Ai cũng làm ra bộ mặt nghiêm chỉnh, song le sự thật thì vẫn thì thầm với nhau chuyện về vợ con, về nhà cửa, về một cái tủ mới sắm, một cái áo mới may. Trong mấy trăm người đi đưa thì một nửa là phụ nữ, phần nhiều tân thời, bạn của cô Tuyết, bà Văn Minh, cô Hoàng Hôn, bà Phó Đoan, vân vân... Thật là đủ giai thanh gái lịch, nên họ chim nhau, cười tình với nhau, bình phẩm nhau, chê bai nhau, ghen tuông nhau, hẹn hò nhau, bằng những vẻ mặt buồn rầu của những người đi đưa ma.
(Hạnh phúc của một tang gia – Vũ Trọng Phụng)
Bút pháp nghệ thuật nổi bật nhất của tác giả trong đoạn trích là:
 Xem đáp án
Xem đáp án
Ở câu hỏi này, HS cần đọc kĩ đoạn trích, kết hợp với hình dung, tưởng tượng nhớ lại văn bản Hạnh phúc một tang gia - Vũ Trọng Phụng. Đây là cảnh “đám ma gương mẫu” được tổ chức long trọng, hoành tráng, giàu tính tạo hình. Tạo nên một cảnh hết sức ấn tượng, đám ma dường như mất đi không khí thông thường mà trở nên hỗn độn, hài hước. Chọn C.
Câu 88:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Đâu những ngày xưa, tôi nhớ tôi
Băn khoăn đi kiếm lẽ yêu đời
Vơ vẩn theo mãi vòng quanh quẩn
Muốn thoát, than ôi, bước chẳng rời
Rồi một hôm nào, tôi thấy tôi
Nhẹ nhàng như con chim cà lơi
Say đồng hương nắng vui ca hát
Trên chín tầng cao bát ngát trời...
(Nhớ đồng – Tố Hữu)
Nội dung chính của đoạn trích trên là gì?
 Xem đáp án
Xem đáp án
Đoạn trích thể hiện nỗi niềm khát khao tự do của tác giả. Chọn A.
Câu 89:
Đọc đoạn trích sau và trả lời câu hỏi:
Mưa đổ bụi êm êm trên bến vắng,
Đò biếng lười nằm mặc nước sông trôi;
Quán tranh đứng im lìm trong vắng lặng
Bên chòm xoan hoa tím rụng tơi bời
Ngoài đường đê cỏ non tràn biếc cỏ,
Đàn sáo đen sà xuống mổ vu vơ
Mấy cánh bướm rập rờn trôi trước gió.
Những trâu bò thong thả cúi ăn mưa.
(Chiều xuân – Anh Thơ)
Nội dung chính của bức tranh chiều xuân là gì?
 Xem đáp án
Xem đáp án
Nội dung chính của bức tranh chiều xuân trong đoạn thơ là bức tranh con người và cảnh vật êm đềm, nhẹ nhàng. Chọn C.
Câu 90:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Mạn thuật (bài 4)
(Nguyễn Trãi)
Đủng đỉnh chiều hôm dắt tay,
Trong thế giới phút chim bay.
Non cao non thấp mây thuộc,
Cây cứng cây mềm gió hay.
Nước mấy trăm thu còn vậy,
Nguyệt bao nhiêu kiếp nhẫn nay*.
Ngoài chưng mọi chốn đều thông hết,
Bui một lòng người cực hiểm thay.
* nhẫn nay: cho đến bây giờ.
Theo bài thơ, thứ gì trong thế giới này thực khó đoán biết?
 Xem đáp án
Xem đáp án
Theo bài thơ: Non cao non thấp mây thuộc, Cây cứng cây mềm gió hay. Nước mấy trăm thu còn vậy, Nguyệt bao nhiêu kiếp nhẫn nay → núi non, cây cối, trăng nước đều dễ đoán biết. Riêng chỉ có lòng người trong thế giới này thực khó đoán biết: Bui một lòng người cực hiểm thay. Chọn C.
Câu 91:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Bèo dạt về đâu, hàng nối hàng;
Mênh mông không một chuyến đò ngang.
Không cầu gợi chút niềm thân mật,
Lặng lẽ bờ xanh tiếp bãi vàng.
(Tràng Giang – Huy Cận)
Cái cảm giác trống trải, xa vắng của không gian “tràng giang” trong khổ thơ, chủ yếu được tô đậm bởi yếu tố nghệ thuật nào?
 Xem đáp án
Xem đáp án
Từ phủ định: Không đò… không cầu... Điệp từ: không. Chọn C.
Câu 92:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Nhiều năm đã trôi qua. Tôi sống ở Thành phố Hồ Chí Minh thỉnh thoảng có việc phải ra Hà Nội đều ghé lại thăm cô Hiền. Chú tôi đã mất rồi. Các em đã có gia đình riêng. Chúng nó cũng đã bắt đầu già. Lớp các cụ trong họ chỉ còn vài người, cô Hiền là một. Cô đã yếu nhiều, đã già hẳn, ngoài bảy mươi rồi còn gì, nhưng cô vẫn là người của hôm nay, một người Hà Nội của hôm nay, thuần tuý Hà Nội, không pha trộn. Nơi tiếp khách của cô sau tấm bình phong cao hơn đầu người bằng gỗ chạm suốt mấy chục năm không hề thay đổi. Một bộ xa lông gụ “cái khánh”, cái sập gụ chân quỳ chạm rất đẹp nhưng không khảm, cái tủ chùa một cánh bên trong bày một cái lọ men Thuý hồng, một cái lư hương đời Hán, một cái liễn hấp sâm Giang Tây, và mấy thứ bình lọ màu men thì thường nhưng có dáng lạ, chả rõ từ đời nào. Cô đang lau đánh một cái bát thuỷ tiên men đỏ, hai cái đầu rồng gắn nối bằng đồng, miệng chân cũng đều bịt đồng, thật đẹp. Bên ngoài trời rét, mưa rây lả lướt chỉ đủ làm ẩm áo chứ không làm ướt, lại nhìn một bà lão (nếu là một thiếu nữ thì phải hơn) lau đánh cái bát bày thuỷ tiên thấy Tết quá, Hà Nội quá, muốn ở thêm ít ngày ăn lại một cái Tết Hà Nội.
(Trích Một người Hà Nội – Nguyễn Khải)
Hình ảnh cái bát thủy tiên men đỏ (gạch chân, in đậm) trong đoạn trích trên có ý nghĩa gì?
 Xem đáp án
Xem đáp án
Hình ảnh bát thủy tiên men đỏ trong đoạn trích trên có ý nghĩa mang đậm những giá trị truyền thống, thể hiện nét đẹp văn hóa của người Hà Nội xưa. Chiếc bát thủy tiên men đỏ được nhắc đến trong đoạn trích với những chi tiết tỉ mỉ, được thiết kế theo phong cách xưa và nhân vật cô Hiền đang cẩn thận lau chùi, chăm sóc nó. Điều đó thể hiện cô Hiền rất trân trọng, giữ gìn cái bát như đang giữ gìn chính truyền thống tốt đẹp của người Hà Nội. Chọn D.
Câu 93:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Có một dòng thi ca về sông Hương, và tôi hi vọng đã nhận xét một cách công bằng về nó khi nói rằng dòng sông ấy không bao giờ tự lặp lại mình trong cảm hứng của các nghệ sĩ. Mỗi nhà thơ đều có một khám phá riêng về nó: từ xanh biếc thường ngày, nó bỗng thay màu thực bất ngờ, “Dòng sông trắng - lá cây xanh” trong cái nhìn tinh tế của Tản Đà, từ tha thướt mơ màng nó chợt nhiên hùng tráng lên “như kiếm dựng trời xanh” trong khí phách của Cao Bá Quát; từ nỗi quan hoài vạn cổ với bóng chiều bảng lảng trong hồn thơ Bà Huyện Thanh Quan, nó đột khởi thành sức mạnh phục sinh của tâm hồn trong thơ Tố Hữu. Và ở đây, một lần nữa, sông Hương quả thực là “Kiều”, rất “Kiều” trong cái nhìn thắm thiết tình người của tác giả “Từ ấy”.
(Ai đã đặt tên cho dòng sông – Hoàng Phủ Ngọc Tường)
Trong đoạn trích trên, vẻ đẹp của sông Hương được khám phá từ góc nhìn nào?
 Xem đáp án
Xem đáp án
Dựa vào câu văn đầu tiên có thể thấy vẻ đẹp của sông Hương được khám phá từ góc nhìn thơ ca. Chọn B.
Câu 94:
Đọc đoạn trích sau và trả lời câu hỏi:
Trước khi về đến vùng châu thổ êm đềm, nó đã là một bản trường ca của rừng già, rầm rộ giữa bóng cây đại ngàn, mãnh liệt qua những ghềnh thác, cuộn xoáy như cơn lốc vào những đáy vực bí ẩn, và cũng có lúc nó trở nên dịu dàng và say đắm giữa những dặm dài chói lọi màu đỏ của hoa đỗ quyên rừng. Giữa lòng Trường Sơn, sông Hương đã sống một nửa cuộc đời của mình như một cô gái Di-gan phóng khoáng và man dại. Rừng già đã hun đúc cho nó một bản lĩnh gan dạ, một tâm hồn tự do và trong sáng.
(Ai đã đặt tên cho dòng sông – Hoàng Phủ Ngọc Tường)
Trong đoạn trích, nghệ thuật viết kí xuất sắc của Hoàng Phủ Ngọc Tường đã được thể hiện ở phương diện nào?
 Xem đáp án
Xem đáp án
Căn cứ vào hình thức của câu văn thứ nhất trong đoạn trích: Trước khi về đến vùng châu thổ êm đềm, nó đã là một bản trường ca của rừng già, rầm rộ giữa bóng cây đại ngàn, mãnh liệt qua những ghềnh thác, cuộn xoáy như cơn lốc vào những đáy vực bí ẩn, và cũng có lúc nó trở nên dịu dàng và say đắm giữa những dặm dài chói lọi màu đỏ của hoa đỗ quyên rừng. Đây là một câu văn dài với nhiều vế ngắt liên tiếp. Chọn A.
Câu 95:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thư viết cho em nhòe nét mực
Phên thưa sương muối cứ bay vào
Núi rét đêm qua chừng mất ngủ
Sáng ra thêm bạc một nhành lau.
Ở đây tuyết trắng bên chăn mỏng
Bếp đỏ cơm trưa núi vẫn mờ
Mực đóng thành băng trong ruột bút
Hơ hoài than đỏ chảy thành thư.
(Hữu Thỉnh, Thư mùa đông, https://phunuquandoi.vn)
Chi tiết nào không gợi tả điều kiện khắc nghiệt của thời tiết?
 Xem đáp án
Xem đáp án
Chi tiết không gợi tả điều kiện khắc nghiệt của thời tiết trong đoạn thơ là “bếp đỏ cơm trưa”. Chọn D.
Câu 96:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Đan Thiềm (thất vọng): - Chỉ tại ông không nghe tôi, dùng dằng mãi. Bây giờ… (Nói với Ngô Hạch) Xin tướng quân…
Ngô Hạch: Dẫn nó đi, không cho nó nói nhảm nữa, rờm tai (quân sĩ dẫn nàng ra)
Đan Thiềm: Ông Cả! Đài lớn tan tành! Ông Cả ơi! Xin cùng ông vĩnh biệt! (Họ kéo nàng ra tàn nhẫn)
(Trích Vĩnh biệt Cửu Trùng Đài – Nguyễn Huy Tưởng)
Bi kịch của Vũ Như Tô là gì?
 Xem đáp án
Xem đáp án
Bi kịch của Vũ Như Tô chính là bi kịch của người nghệ sĩ không giải quyết được mối quan hệ giữa khát vọng nghệ thuật và hiện thực xã hội; giữa người nghệ sĩ và công dân. Chọn B.
Câu 97:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Quyện điểu quy lâm tầm túc thụ
Cô vân mạn mạn độ thiên không.
(Chiều tối – Hồ Chí Minh)
Âm hưởng chủ đạo của hai câu thơ trên là gì?
 Xem đáp án
Xem đáp án
Hai câu thơ có nghĩa là: Chim bay về núi khi trời tối, chòm mây trôi lững lờ giữa tầng không. Trời sắp tối mà người tù vẫn đang bị giải đi trên đường chuyển lao, cả ngày dài không được nghỉ ngơi. Không gian, thời gian, cảnh vật gợi lên sự mệt mỏi, cô quạnh của người tù. Chọn C.
Câu 98:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Khi mỗi mùa rau khúc nở một màu trắng mơ hồ như sương đọng trên những cánh đồng thì trong tôi lại vang lên một câu hỏi. Câu hỏi năm nào cũng vang lên trong tôi và kéo dài mấy chục năm rồi. Một câu hỏi đơn giản đến mức hình như chẳng có ai một lần đặt câu hỏi đó trong cuộc đời mình: Làm thế nào mà những cây rau khúc bé bỏng lại có thể giữ được sự sống của chúng trong đất suốt một năm trời qua mưa bão, nắng gió và đến một ngày lại thức dậy tràn đầy sức sống như thế?. Những hạt rau khúc nhỏ li ti như những hạt bụi. Chúng vùi sâu trong đất với mưa nắng, ngập lụt và bao biến động mà không bị giết chết. Ai cho những hạt rau khúc bé bỏng kia sức mạnh phi thường và sự chịu đựng bền bỉ đến như vậy? Có những câu hỏi về những điều thật nhỏ bé lại chứa đựng cả một bí ẩn lớn của vũ trụ. Và những thứ nhỏ bé ấy lại là “biển” chỉ đường cho con người trong đời sống hầu như mù mờ và vô định này.
(Tôi khóc những cánh đồng rau khúc, Nguyễn Quang Thiều)
Từ “chúng” trong câu văn “Chúng vùi sâu trong đất với mưa nắng, ngập lụt và bao biến động mà không bị giết chết.” thay thế cho đối tượng nào trước đó?
 Xem đáp án
Xem đáp án
Dựa vào câu văn trước đó: Những hạt rau khúc nhỏ li ti như những hạt bụi. Chúng vùi sâu trong đất với mưa nắng, ngập lụt và bao biến động mà không bị giết chết. Nên từ “chúng” ở đây chỉ những hạt rau khúc. Chọn D.
Câu 99:
Đọc đoạn trích sau và trả lời câu hỏi:
Từ lưng đèo
Dốc núi mù che
Các anh về
Xôn xao làng tôi bé nhỏ
Nhà lá đơn sơ
Nhưng tấm lòng rộng mở
Nồi cơm nấu dở
Bát nước chè xanh
Ngồi vui kể chuyện tâm tình bên nhau.
(Bao giờ trở lại – Hoàng Trung Thông)
Đoạn thơ trên diễn tả tình cảm nào sau đây?
 Xem đáp án
Xem đáp án
Đoạn thơ diễn tả tình quân dân ấm áp giữa những người vệ quốc quân với nhân dân. Chọn D.
Câu 100:
Đọc đoạn trích sau đây và trả lời câu hỏi:
“Lính đảo hát tình ca trên đảo” của Trần Đăng Khoa là một bài thơ hay, để lại ấn tượng sâu sắc từ khi ra đời cho đến nay. Từ cấu tứ, hình ảnh, giọng điệu, tất cả đọc lên cứ vừa tếu táo, bông đùa nhưng lại cảm thương sâu sắc về cuộc đời người lính biển. Họ trở thành tượng đài bất khuất giữa trùng khơi, như một minh chứng cho lòng quả cảm, sự kiên cường của một dân tộc chưa bao giờ khuất phục, sẵn sàng “quyết tử cho Tổ quốc quyết sinh”. Tình ca và hùng ca, hóm hỉnh và lắng đọng, trần trụi và đầy suy tư,... là những trạng thái cảm xúc hài hoà, gắn kết xuyên suốt bài thơ [...] Qua đó, khơi dậy niềm tự hào và tình yêu biển đảo đối với thế hệ trẻ, nhất là ca ngợi vẻ đẹp hào hùng của người lính biển trong vai trò bảo vệ chủ quyền đất nước trong giai đoạn hiện nay.
(Lính đảo hát tình ca trên đảo, Lê Thành Văn)
Đối tượng nào được nhận xét, đánh giá đề cập đến trong đoạn trích trên?
 Xem đáp án
Xem đáp án
Đối tượng được nhận xét, đánh giá đề cập đến trong đoạn trích là bài thơ “Lính đảo hát tình ca trên đảo” của Trần Đăng Khoa. Chọn B.
Câu 101:
PHẦN 3: KHOA HỌC
Lĩnh vực: Khoa học tự nhiên và xã hội (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Ở Việt Nam những năm đầu thế kỉ XX, đại diện tiêu biểu nhất của con đường cứu nước theo xu hướng cải cách là Phan Châu Trinh, khuynh hướng bạo động là Phan Bội Châu. Chọn B.
Câu 102:
 Xem đáp án
Xem đáp án
Từ năm 1957-1959: Ngô Đình Diệm ban hành chính sách "tố cộng, diệt cộng", ra đạo luật 10/59 đặt cộng sản ra ngoài vòng pháp luật, lê máy chém khắp miền Nam làm lực lượng cách mạng bị tổn thất nặng, đòi hỏi phải có biện pháp quyết liệt để đưa cách mạng vượt qua khó khăn. Tháng 1-1959, Hội nghị Trung ương Đảng 15 xác định: cách mạng miền Nam không có con đường nào khác là sử dụng bạo lực cách mạng đánh đổ chính quyền Mĩ-Diệm.
Từ đó phong trào Đồng khởi đã nổ ra khắp miền Nam thành cao trào cách mạng. Chọn A.
Câu 103:
 Xem đáp án
Xem đáp án
Nguyễn Tất Thành rất khâm phục tinh thần yêu nước của các bậc tiền bối (Phan Bội Châu và Phan Châu Trinh), nhưng không tán thành con đường của họ, nên quyết định tìm con đường cứu nước mới; Được tiếp xúc với văn minh Pháp, Nguyễn Tất Thành quyết định sang phương Tây để tìm hiểu xem nước Pháp và các nước khác làm thế nào, rồi trở về giúp đồng bào, giải phóng dân tộc. Chọn C.
Câu 104:
 Xem đáp án
Xem đáp án
Năm 1972, Xô-Mĩ thỏa thuận hạn chế vũ khí chiến lược, kí Hiệp ước ABM (Hiệp ước Chống tên lửa đạn đạo), SALT-1 (Hiệp định hạn chế vũ khí tiến công chiến lược), đánh dấu sự hình thành thế cân bằng về quân sự và vũ khí hạt nhân chiến lược giữa hai cường quốc.
Đây chính là biểu hiện xu hướng hòa hoãn Đông-Tây, và những hiệp ước này góp phần làm giảm tình trạng đối đầu trong quan hệ quốc tế. Chọn B.
Câu 105:
 Xem đáp án
Xem đáp án
Cuộc Tổng tiến công và nổi dậy Tết Mậu Thân vẫn hết sức to lớn đã làm lung lay ý chí xâm lược quân Mĩ, buộc Mĩ phải tuyên bố "phi Mĩ hóa" chiến tranh xâm lược (tức thừa nhận thất bại của "Chiến tranh cục bộ"), ngừng mọi hoạt động bắn phá miền Bắc và ngồi vào bàn đàm phán với ta ở Paris để chấm dứt chiến tranh, đồng thời mở ra bước ngoặt của cuộc kháng chiến chống Mĩ cứu nước. Chọn C.
Câu 106:
 Xem đáp án
Xem đáp án
Ý nghĩa quan trọng nhất của phong trào yêu nước dân chủ tư sản ở Việt Nam trong những năm 20 của thế kỉ XX góp phần khảo sát và thử nghiệm một con đường cứu nước mới theo khuynh hướng tư sản. Qua phong trào yêu nước dân chủ tư sản đã cho thấy con đường cứu nước theo dân chủ tư sản không thể thắng lợi ở Việt Nam. Buộc Việt Nam phải Chọn C.on đường theo khuynh hướng vô sản để đi tới thắng lợi cuối cùng. Chọn B.
Câu 107:
 Xem đáp án
Xem đáp án
Chiến dịch Biên giới thu-đông năm 1950 ở Việt Nam được mở trong bối cảnh lịch sử Mĩ đang từng bước can thiệp vào chiến tranh ở Việt Nam. Chọn C.
Câu 108:
 Xem đáp án
Xem đáp án
Nava tập trung mọi cố gắng để xây dựng Điện Biên Phủ thành một tập đoàn cứ điểm mạnh nhất Đông Dương. Tồng số binh lực ở đây lúc cao nhất là 16200 quân, được bố trí thành ba phân khu với 49 cứ điểm. Sau khi kiểm tra, các tướng lĩnh Pháp và Mĩ đều coi Điện Biên Phủ là "một pháo đài bất khả xâm phạm". Chọn C.
Câu 109:
 Xem đáp án
Xem đáp án
Quân Pháp xây dựng Điện Biên Phủ thành tập đoàn cứ điểm mạnh nhất Đông Dương, vì nơi đây có vị trí then chốt ở Đông Dương và Đông Nam Á. Điện Biên Phủ là một thung lũng nằm ở phía Tây vùng rừng núi Tây Bắc, gần biên giới Lào, cách Hà Nội 300 km, cách Luông Pha Băng 200 km, cách hậu phương của ta (Việt Bắc, Thanh Nghệ Tĩnh) từ 300 km đến 500 km. Với Pháp đây là một vị trí chiến lược then chốt, có thể trở thành một căn cứ lục quân và không quân trong âm mưu xâm lược của chúng ở Đông Dương và Đông Nam Á về lâu dài. Chọn B.
Câu 110:
 Xem đáp án
Xem đáp án
Phương châm của chiến dịch Điện Biên Phủ (1954) của quân đội Việt Nam là "Đánh chắc, tiến chắc" được lựa chọn chỉ vài giờ trước khi ta chính thức đương đầu với Pháp, nhằm chuẩn bị kĩ càng nhất cho một trận chắc thắng, theo đúng lò̀i dặn của Bác Hồ trước chiến dịch. Chọn C.
Câu 111:
 Xem đáp án
Xem đáp án
Địa hình nhiều đồi núi không phải điều kiện thuận lợi để phát triển nông nghiệp ở ĐNA. Đồi núi đòi hỏi phải có các biện pháp kỹ thuật để canh tác. Chọn D.
Câu 112:
 Xem đáp án
Xem đáp án
Biểu hiện của nền kinh tế tri thức ở Hoa Kỳ không phải là phân bố công nghiệp về phía nam. Yếu tố này không nói đến kinh tế tri thức. Chọn C.
Câu 113:
 Xem đáp án
Xem đáp án
Tính chất nhiệt đới của biển Đông được thể hiện rõ trong đặc điểm về nhiệt độ → Chọn A.
Câu 114:
 Xem đáp án
Xem đáp án
Hiện tượng "nồm" của thời tiết miền Bắc vào cuối mùa đông-đầu mùa xuân chủ yếu do gió tín phong bán cầu bắc nào gây nên. Lúc này miền Bắc đang lạnh, gặp gió tín phong nóng đột ngột nên "nồm". Chọn C.
Câu 115:
 Xem đáp án
Xem đáp án
Mỏ Tiền Hải thuộc vịnh Bắc Bộ. Chọn A.
Câu 116:
Cho biểu đồ:
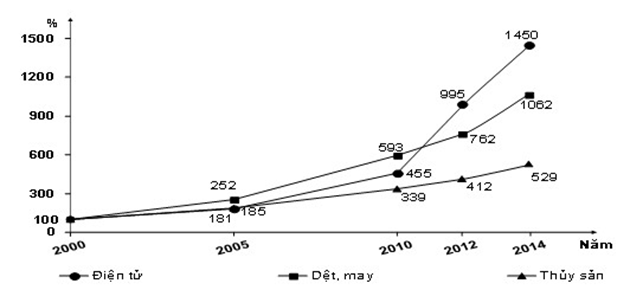
Tốc độ tăng trưởng một số mặt hàng xuất khẩu của Việt Nam
Căn cứ vào biểu đồ đã cho, hãy cho biết nhận xét nào sau đây là không đúng về tốc độ tăng trưởng một số mặt hàng xuất khẩu của Việt Nam?
 Xem đáp án
Xem đáp án
Phân tích nội dung các đáp án, ta thấy:
- A đúng: hàng dệt -may có tốc độ tăng trưởng lớn thứ 2 (từ 100% lên 1062%)
- B đúng: giai đoạn 2000-2010 hàng dệt-may có tốc độ tăng trưởng cao nhất (từ 100% lên 593%)
- C không đúng: giai đoạn 2000-2005 hàng điện tử có tốc độ tăng trưởng thấp nhất và năm 2010 tốc độ tăng trưởng đứng thứ 2 → nhận xét tốc độ tăng trưởng hàng điện tử luôn cao nhất trong suốt giai đoạn 2000-2014 là SAI. Chọn C.
Câu 117:
 Xem đáp án
Xem đáp án
Do áp dụng rộng rãi các biện pháp thâm canh nông nghiệp, đưa vào sử dụng đại trà các giống mới, nên năng suất lúa nước ta tăng mạnh, nhất là vụ lúa đông xuân. Chọn A.
Câu 118:
 Xem đáp án
Xem đáp án
Nội thương của nước ta hiện nay đã thu hút sự tham gia của nhiều thành phần kinh tế. Chọn D.
Câu 119:
 Xem đáp án
Xem đáp án
ĐBSH có nhiều điều kiện thuận lợi để phát triển trở thành vùng trọng điểm sản xuất lương thực, thục phẩm là: đất phù sa màu mỡ với diện tích lớn (70%), khí hậu nhiệt đới ẩm gió mùa với nguồn nhiệtẩm dồi dào, lượng mưa lớn rất thích hợp với cây lúa nước. Chọn C.
Câu 120:
 Xem đáp án
Xem đáp án
DHTNB có đường bờ biển dài, ngư trường trọng điểm: Hoàng Sa, Trường Sa, Ninh Thuận, Bình Thuận → Nghề cá duyên hải NTB phát triển mạnh hơn BTB. Chọn D.
Câu 121:
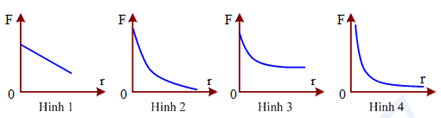
Đồ thị nào trong các đồ thị dưới đây có thể biểu diễn sự phụ thuộc của lực tương tác giữa hai điện tích điểm vào khoảng cách giữa chúng?
 Xem đáp án
Xem đáp án
Lực tương tác giữa hai điện tích điểm được xác định bởi công thức: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\).
Hay \(F \sim \frac{1}{{{r^2}}}\).
+ Khi \(r \to \infty \Rightarrow F \to 0\).
+ Khi \(r \to 0 \Rightarrow F \to \infty \).
\( \Rightarrow \) Đồ thị \(F\left( r \right)\) có dạng đường hypebol \( \Rightarrow \) Hình 4. Chọn D.
Câu 122:
Một nam châm thẳng N-S đặt thẳng đứng gần khung dây tròn. Trục của nam châm vuông góc với mặt phẳng của khung dây. Giữ khung dây đứng yên. Lần lượt cho nam châm chuyển động như sau:
I. Tịnh tiến dọc theo trục của nó.
II. Quay nam châm quanh trục thẳng đứng của nó.
III. Quay nam châm quanh một trục nằm ngang và vuông góc với trục của nam châm.
Các trường hợp có dòng điện cảm ứng xuất hiện trong khung dây là
 Xem đáp án
Xem đáp án
Dòng điện cảm ứng xuất hiện khi từ thông qua khung dây biến thiến. Chọn B.
Câu 123:
 Xem đáp án
Xem đáp án
Gọi O là vị trí của con cá trong nước.
Do hiện tượng khúc xạ và do chiết suất của nước lớn hơn chiết suất của không khí nên ảnh của con cá sẽ ở vị trí O’ như hình vẽ.
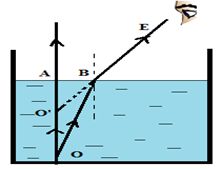
Như vậy, người đó nhìn thấy con cá dường như gần mặt nước hơn. Để đâm trúng con cá thì người đó phải phóng mũi lao vào phía dưới vị trí mà người đó nhìn thấy con cá. Chọn C.
Câu 124:
Một con lắc đơn dao động với biên độ \({\alpha _0} < \frac{\pi }{2}\), có mốc thế năng được chọn tại vị trí cân bằng của vật nặng. Gọi độ lớn vận tốc của vật nặng khi động năng bằng thế năng là v1, khi độ lớn của lực căng dây treo bằng trọng lực tác động lên vật là v2. Tỉ số \(\frac{{{v_1}}}{{{v_2}}}\) có giá trị nào sau đây?
 Xem đáp án
Xem đáp án
+ Khi động năng bằng thế năng: \[{W_t} = {W_d} \Rightarrow {W_t} = W - {W_t}\]
\[ \Leftrightarrow mg\ell .\left( {1 - \cos {\alpha _1}} \right) = mg\ell .\left( {1 - \cos {\alpha _0}} \right) - mg\ell .\left( {1 - \cos {\alpha _1}} \right)\]
\[ \Leftrightarrow 1 - \cos {\alpha _1} = \cos {\alpha _1} - \cos {\alpha _0}\]
\[ \Leftrightarrow \cos {\alpha _1} = \frac{1}{2} + \frac{1}{2}.\cos {\alpha _0}\]
+ Khi độ lớn của lực căng dây treo bằng trọng lực tác dụng lên vật:
\[mg.\left( {3\cos {\alpha _2} - 2\cos {\alpha _0}} \right) = mg\]\[ \Leftrightarrow 3\cos {\alpha _2} - 2\cos {\alpha _0} = 1 \Leftrightarrow \cos {\alpha _2} = \frac{1}{3} + \frac{2}{3}.\cos {\alpha _0}\]
+ Khi đó: \[\frac{{{v_1}}}{{{v_2}}} = \frac{{\sqrt {2g\ell \left( {\cos {\alpha _1} - \cos {\alpha _0}} \right)} }}{{\sqrt {2g\ell \left( {\cos {\alpha _2} - \cos {\alpha _0}} \right)} }} = \sqrt {\frac{{\cos {\alpha _1} - \cos {\alpha _0}}}{{\cos {\alpha _2} - \cos {\alpha _0}}}} \]
\[ = \sqrt {\frac{{\frac{1}{2} + \frac{1}{2}.\cos {\alpha _0} - \cos {\alpha _0}}}{{\frac{1}{3} + \frac{2}{3}.\cos {\alpha _0} - \cos {\alpha _0}}}} = \sqrt {\frac{{\frac{1}{2}\left( {1 - \cos {\alpha _0}} \right)}}{{\frac{1}{3}\left( {1 - \cos {\alpha _0}} \right)}}} = \sqrt {\frac{3}{2}} \]. Chọn D.
Câu 125:
 Xem đáp án
Xem đáp án
Từ đồ thị ta thấy chu kì sóng âm là: \[T = 4.0,20 = 0,8ms = {8.10^{ - 4}}s\]
\[ \Rightarrow \] Tần số của âm do âm thoa tạo ra là: \[f = \frac{1}{T} = \frac{1}{{{{8.10}^{ - 4}}}} = 1250Hz\].
Chọn B.
Câu 126:
Một nhà vật lý hạt nhân làm thí nghiệm xác định chu kì bán rã \(\left( T \right)\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \(\left( {\Delta N} \right)\) và số hạt ban đầu \(\left( {{N_0}} \right)\). Dựa vào kết quả thực nghiệm đo được trên hình vẽ, hãy tính \(T\)?
 Xem đáp án
Xem đáp án
Ta có: \({\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \frac{1}{{1 - \frac{{\Delta N}}{{{N_0}}}}} = \frac{1}{{1 - \left( {1 - {2^{ - \frac{t}{T}}}} \right)}} = \frac{1}{{{2^{ - \frac{t}{T}}}}} = {2^{\frac{t}{T}}}\)\( \Rightarrow \ln {\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \ln \left( {{2^{\frac{t}{T}}}} \right)\)
Từ đồ thị ta thấy: \(\left\{ {\begin{array}{*{20}{l}}{t = 6ngay}\\{\ln {{\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)}^{ - 1}} = 0,467}\end{array}} \right. \Rightarrow \ln \left( {{2^{\frac{6}{T}}}} \right) = 0,467 \Rightarrow T = 8,9\) ngày. Chọn D.
Câu 127:
Một máy phát sóng điện từ đặt cách mặt phản xạ 45 cm. Các sóng phát ra có tần số là 1 GHz. Một sóng dừng được tạo ra với một nút tại máy phát và một nút ở bề mặt. Có bao nhiêu bụng sóng trong không gian giữa máy phát và mặt phản xạ?
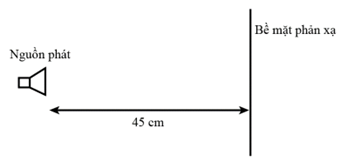
 Xem đáp án
Xem đáp án
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\ell = 45\,cm = 0,45\,m}\\{v = c = {{3.10}^8}m/s}\\{f = 1GHz = {{10}^9}Hz}\end{array}} \right.\)
Một sóng dừng được tạo ra với một nút tại máy phát và một nút ở bề mặt.
Áp dụng điều kiện có sóng dừng với hai đầu là nút sóng ta có:
\(\ell = \frac{{k\lambda }}{2} = \frac{{k.v}}{{2f}} \Rightarrow k = \frac{{2.\ell .f}}{v} = \frac{{2.0,{{45.10}^9}}}{{{{3.10}^8}}} = 3\)
\( \Rightarrow \) Có 3 bụng sóng trong không gian giữa máy phát và mặt phản xạ. Chọn C.
Câu 128:
Một học sinh làm thí nghiệm đo bước sóng ánh sáng bằng thí nghiệm khe Y-âng. Trong khi tiến hành, học sinh này đo được khoảng cách hai khe sáng là \(1,00 \pm 0,05\left( {mm} \right)\); khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \(2000 \pm 1,54\left( {mm} \right)\); khoảng cách giữa 10 vân sáng liên tiếp đo được là \(10,80 \pm 0,14\left( {mm} \right)\). Sai số tuyệt đối của quá trình đo bước sóng là
 Xem đáp án
Xem đáp án
Khoảng cách giữa 10 vân sáng liên tiếp là: \(\ell = 9i \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\bar i = \frac{{\overline \ell }}{9} = 1,2{\mkern 1mu} {\mkern 1mu} \left( {mm} \right)}\\{\Delta i = \frac{{\Delta \ell }}{9} = 0,016{\mkern 1mu} {\mkern 1mu} \left( {mm} \right)}\end{array}} \right.\)
Giá trị trung bình của bước sóng là: \(\bar \lambda = \frac{{\bar a.\bar i}}{{\bar D}} = \frac{{{{1.10}^{ - 3}}.1,{{2.10}^{ - 3}}}}{2} = 0,{6.10^{ - 6}}{\mkern 1mu} {\mkern 1mu} \left( m \right) = 0,6{\mkern 1mu} {\mkern 1mu} \left( {\mu m} \right)\)
Sai số tỉ đối của phép đo là: \(\frac{{\Delta \lambda }}{{\bar \lambda }} = \frac{{\Delta a}}{{\bar a}} + \frac{{\Delta i}}{{\bar i}} + \frac{{\Delta D}}{{\bar D}}\)\( \Rightarrow \frac{{\Delta \lambda }}{{0,6}} = \frac{{0,05}}{1} + \frac{{0,016}}{{1,2}} + \frac{{1,54}}{{2000}}\)
\( \Rightarrow \Delta \lambda \approx \pm 0,038{\mkern 1mu} {\mkern 1mu} \left( {\mu m} \right)\). Chọn B.
Câu 129:
 Xem đáp án
Xem đáp án
Vật liệu chính sử dụng trong một pin quang điện là bán dẫn. Chọn D.
Câu 130:
Đặt điện áp \(u = {U_0}\cos \omega t\) vào hai đầu đoạn mạch AB như hình bên. Trong đó, cuộn cảm thuần có độ tự cảm L; tụ điện có điện dung C; X là đoạn mạch chứa các phần tử có \({R_1},{L_1},{C_1}\) mắc nối tiếp. Biết \(2{\omega ^2}LC = 1\), các điện áp hiệu dụng: \({U_{AN}} = 120V;{U_{MB}} = 90V\), góc lệch pha giữa \({u_{AN}}\) và \({u_{MB}}\) là \(\frac{{5\pi }}{{12}}\). Hệ số công suất của X là
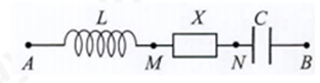
 Xem đáp án
Xem đáp án
Ta có: \(2LC{\omega ^2} = 1 \Leftrightarrow \frac{{2\omega L}}{{\frac{1}{{\omega C}}}} = 1 \Rightarrow 2{Z_L} = {Z_C}\)
\( \Rightarrow 2{u_L} = - {u_C} \Rightarrow 2{u_L} + {u_C} = 0\)\( \Rightarrow 2{u_{AN}} + {u_{MB}} = 2{u_L} + 2{u_X} + {u_X} + {u_C}\)\( \Rightarrow 2{u_{AN}} + {u_{MB}} = 3{u_X}\)
\( \Rightarrow {u_X} = \frac{{2{u_{AN}} + {u_{MB}}}}{3}\)
Giả sử \({\varphi _{uMB}} = 0 \Rightarrow {\varphi _{uAN}} = \frac{{5\pi }}{{12}}\)\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{u_{MB}} = 90\sqrt 2 \cos \left( {\omega t} \right)}\\{{u_{AN}} = 120\sqrt 2 .\cos \left( {\omega t + \frac{{5\pi }}{{12}}} \right)}\end{array}} \right.\)
\( \Rightarrow {u_X} = \frac{{240\sqrt 2 \angle \frac{{5\pi }}{{12}} + 90\sqrt 2 \angle 0}}{3} = 130,7\angle 0,99\)\( \Rightarrow {\varphi _{uX}} = 0,99rad\)
Lại có: \({u_C} = {u_{MB}} - {u_X} = 122,6\angle - 1,1\)\( \Rightarrow {\varphi _i} = {\varphi _{uC}} + \frac{\pi }{2} = - 1,1 + \frac{\pi }{2} \approx 0,47079\,\,rad\)
\( \Rightarrow \) Độ lệch pha giữa \({u_X}\) và \(i\) là: \({\varphi _X} = {\varphi _{uX}} - {\varphi _i} = 0,99 - 0,47079 = 0,51921\,\,rad\)
\( \Rightarrow \) Hệ số công suất của X là: \(\cos {\varphi _X} = \cos 0,51921 = 0,868\). Đáp án. 0,87.
Câu 131:
 Xem đáp án
Xem đáp án
Cách 1:
Dung dịch chứa chất mà ion của chất đó tạo môi trường trung tính sẽ không làm đổi màu của quỳ tím. Một số ion tạo môi trường trung tính thường gặp:
- Ion của kim loại mạnh: \[N{a^ + },{\rm{ }}{K^ + },{\rm{ }}C{a^{2 + }},{\rm{ }}B{a^{2 + }},{\rm{ }}.\]
- Ion của gốc acid mạnh:\[S{O_4}^{2 - },{\rm{ }}N{O_3}^ - ,{\rm{ }}C{l^ - },\]...
→ Chọn \[N{a_2}S{O_4}\]vì \[N{a_2}S{O_4}\]tạo bởi ion \[N{a^ + }\]và \[SO_4^{2 - }\]là các ion tạo môi trường trung tính.
Cách 2: Dùng phương pháp loại trừ:
- HCl là acid nên dung dịch HCl sẽ làm quỳ tím chuyển màu đỏ → Loại.
- \[HCl{O_4}\]là acid nên dung dịch \[HCl{O_4}\] sẽ làm quỳ tím chuyển màu đỏ → Loại.
- \[Ba{\left( {OH} \right)_2}\]là base nên dung dịch \[Ba{\left( {OH} \right)_2}\]sẽ làm quỳ tím chuyển màu xanh → Loại.
→ Dung dịch chất không làm quỳ tím chuyển màu là \[N{a_2}S{O_4}.\]
Chọn B.
Câu 132:
 Xem đáp án
Xem đáp án
Các chất trong cấu tạo có nhóm -CHO có khả năng tham gia phản ứng tráng gương, ví dụ: aldehyde, glucose, HCOOR,..
→ Chọn glucose.
Chọn C.
Câu 133:
Thủy phân hoàn toàn 1 mol pentapeptide X, thu được 2 mol glyin (Gly), 1 mol alanine (Ala), 1 mol valine (Val) và 1 mol phenylalanine (Phe). Thủy phân không hoàn toàn X thu được dipeptide Val-Phe và tripeptide Gly-Ala- Val nhưng không thu được dipeptide Gly-Gly. Chất X có công thức là
 Xem đáp án
Xem đáp án
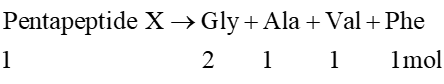
X thủy phân → Val–Phe + Gly–Ala–Val.
Nên X có các liên kết Gly–Ala–Val–Phe.
Vì không thu được Gly–Gly nên X có công thức là Gly–Ala–Val–Phe–Gly.
Chọn C.
Câu 134:
PVC được điều chế từ khí thiên nhiên (chứa 95 % thể tích \[C{H_4}\]) theo sơ đồ chuyển hoá và hiệu suất của mỗi giai đoạn như sau: . Muốn tổng hợp 1 tấn PVC thì cần bao nhiêu \[{m^3}\] khí thiên nhiên ở đktc?
 Xem đáp án
Xem đáp án
![PVC được điều chế từ khí thiên nhiên (chứa 95 % thể tích \[C{H_4}\]) theo sơ đồ chuyển hoá và hiệu suất của mỗi giai đoạn như sau: . Muốn tổng hợp 1 tấn PVC thì cần bao nhiêu \[{m^3}\] khí thiên nhiên ở đktc? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid8-1721713000.png)
Do hiệu suất của mỗi quá trình phản ứng lần lượt là 15%, 95%, 90% và khí thiên nhiên chỉ chứa 95% thể tích \[C{H_4}.\]
Nên thể tích khí thiên nhiên thực tế là: \(V = \frac{{22,4.0,{{032.10}^6}}}{{0,15.0,95.0,9.0,95}} = {5883.10^3}\) lít \( = 5883\;{{\rm{m}}^3}\).
Chọn B.
Câu 135:
Tiến hành thí nghiệm oxi hóa glucose bằng dung dịch \[AgN{O_3}\] trong \[N{H_3}\] (phản ứng tráng bạc) theo các bước sau:
Bước 1: Cho 1 ml dung dịch \[AgN{O_3}1\% \] vào ống nghiệm sạch.
Bước 2: Nhỏ từ từ dung dịch \[N{H_3}\] cho đến khi kết tủa tan hết.
Bước 3: Thêm 3 - 5 giọt glucose vào ống nghiệm.
Bước 4: Đun nóng nhẹ hỗn hợp ở \[60^\circ C{\rm{ }} - {\rm{ }}70^\circ C\] trong vài phút.
Cho các nhận định sau:
(a) Sau bước 2, dung dịch trong ống nghiệm chứa phức diammine silver (I) hydroxide\[\left[ {Ag{{\left( {N{H_3}} \right)}_2}} \right]OH.\]
(b) Ở bước 4, glucose bị oxi hóa tạo thành muối ammonium gluconate.
(c) Kết thúc thí nghiệm thấy thành ống nghiệm sáng bóng như gương.
(d) Ở thí nghiệm trên, nếu thay glucose bằng fructose hoặc saccharose thì đều thu được kết tủa tương tự.
(e) Thí nghiệm trên chứng tỏ glucose là hợp chất tạp chức, phân tử chứa nhiều nhóm –OH và một nhóm -CHO.
Số nhận định đúng là
 Xem đáp án
Xem đáp án
(d) sai, vì saccharose không thực hiện được phản ứng tráng gương.
(e) sai, vì thí nghiệm trên chỉ chứng tỏ glucose chứa 1 nhóm –CHO.
(a), (b) và (c) đúng.
Chọn A.
Câu 136:
Câu 137:
 Xem đáp án
Xem đáp án
Đề bài cho hỗn hợp X gồm formic acid, acrylic acid, oxalic acid và acetic acid tham gia các quá trình phản ứng theo sơ đồ sau:
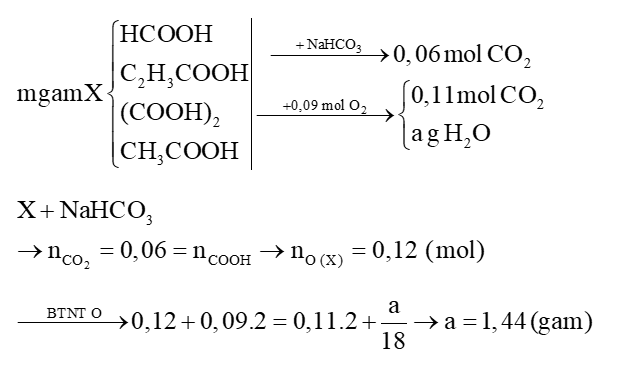
Chọn C.
Câu 138:
Thực hiện các thí nghiệm sau:
(a) Cho dung dịch \[Ba{\left( {HC{O_3}} \right)_2}\]vào dung dịch \[NaHS{O_4}\].
(b) Cho Na vào dung dịch \[FeC{l_2}\]dư.
(c) Cho dung dịch \[{\left( {N{H_4}} \right)_2}S{O_4}\] vào dung dịch \[Ba{\left( {OH} \right)_2}\].
(d) Sục khí \[C{O_2}\] dư vào dung dịch hỗn hợp NaOH và \[Ba{\left( {OH} \right)_2}\].
(e) Cho dung dịch \[AgN{O_3}\] vào dung dịch \[Fe{\left( {N{O_3}} \right)_2}\].
Sau khi các phản ứng kết thúc, số thí nghiệm thu được cả kết tủa và khí là
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{\left( a \right){\rm{ }}Ba{{\left( {HC{O_3}} \right)}_2} + {\rm{ }}2NaHS{O_4} \to {\rm{ }}BaS{O_4} \downarrow + {\rm{ }}N{a_2}S{O_4} + {\rm{ }}2{H_2}O{\rm{ }} + {\rm{ }}2C{O_2} \uparrow }\\{\left( b \right){\rm{ }}2Na{\rm{ }} + {\rm{ }}2{H_2}O{\rm{ }} \to {\rm{ }}2NaOH{\rm{ }} + {\rm{ }}{H_2} \uparrow }\\{\;\;\;\;\;{\rm{ }}FeC{l_2} + {\rm{ }}2NaOH{\rm{ }} \to {\rm{ }}Fe{{\left( {OH} \right)}_2} \downarrow {\rm{ }} + {\rm{ }}2NaCl}\\{\left( c \right){\rm{ }}{{\left( {N{H_4}} \right)}_2}S{O_4} + {\rm{ }}Ba{{\left( {OH} \right)}_2} \to {\rm{ }}BaS{O_4} \downarrow {\rm{ }} + {\rm{ }}2N{H_3} \uparrow {\rm{ }} + {\rm{ }}2{H_2}O}\end{array}\]
(d) \[C{O_2}\]dư nên không thu được kết tủa.
\[\left( e \right){\rm{ }}AgN{O_3} + {\rm{ }}Fe{\left( {N{O_3}} \right)_2} \to {\rm{ }}Fe{\left( {N{O_3}} \right)_3} + {\rm{ }}Ag \downarrow \]
Vậy có 3 phản ứng vừa thu được khí và kết tủa là (a), (b), (c).
Chọn C.
Câu 139:
Quá trình tổng hợp \[N{H_3}\]từ \[{H_2}\]và \[{N_2}\](với xúc tác\[A{l_2}{O_3}\]) có thể được biểu diễn bằng cân bằng hóa học sau:
Người ta thử các cách sau:
(1) tăng áp suất của khí \[{N_2}\]khi cho vào hệ.
(2) tăng áp suất chung của hệ.
(3) giảm nhiệt độ của hệ.
(4) không dùng chất xúc tác nữa.
(5) hóa lỏng \[N{H_3}\]và đưa ra khỏi hệ.
Số cách làm có thể làm cân bằng chuyển dịch theo chiều thuận là
 Xem đáp án
Xem đáp án
Phản ứng có ΔH < 0 ⟹ Phản ứng thuận là phản ứng tỏa nhiệt
- Xét (1): tăng áp suất của khí \[{N_2}\]khi cho vào hệ
⟹ Nồng độ của khí \[{N_2}\] tăng.
⟹ Cân bằng sẽ chuyển dịch theo chiều làm giảm nồng độ của khí \[{N_2}\].
⟹ Cân bằng chuyển dịch theo chiều thuận.
- Xét (2): tăng áp suất chung của hệ
⟹ Cân bằng sẽ chuyển dịch theo chiều làm giảm áp suất của hệ
Ta thấy vế trái có 1 + 3 = 4 mol khí, vế trái có 2 mol khí.
⟹ Cân bằng chuyển dịch theo chiều thuận.
- Xét (3): giảm nhiệt độ của hệ
⟹ Cân bằng sẽ chuyển dịch theo chiều làm tăng nhiệt độ của hệ (tỏa nhiệt).
⟹ Cân bằng chuyển dịch theo chiều thuận.
- Xét (4): chất xúc tác chỉ ảnh hưởng tới tốc độ phản ứng chứ không ảnh hưởng đến sự chuyển dịch cân bằng
- Xét (5): hóa lỏng \[N{H_3}\]và đưa ra khỏi hệ
⟹ Nồng độ \[N{H_3}\]trong hệ giảm.
⟹ Cân bằng sẽ chuyển dịch theo chiều làm nồng độ của \[N{H_3}\]tăng.
⟹ Cân bằng chuyển dịch theo chiều thuận.
Vậy có 4 cách làm cân bằng chuyển dịch theo chiều thuận là 1, 2, 3, 5.
Chọn A.
Câu 140:
Hai ester X, Y có cùng công thức phân tử \[{C_8}{H_8}{O_2}\]và chứa vòng benzene trong phân tử. Cho 6,8 gam hỗn hợp gồm X và Y tác dụng với dung dịch NaOH dư, đun nóng, lượng NaOH phản ứng tối đa là 0,06 mol, thu được dung dịch Z chứa 4,7 gam ba muối. Khối lượng muối của carboxylic acid có phân tử khối lớn hơn trong Z là
 Xem đáp án
Xem đáp án
Khi hỗn hợp gồm X và Y + NaOH thì \[1 < \frac{{{n_{NaOH}}}}{{{n_{ester}}}} = 1,2 < 2\] nên hỗn hợp có một ester tạo từ phenol (giả sử là X)
Thì X + 2NaOH → 2muối + \[{H_2}O\]
Y + NaOH → muối + alcohol
Ta có \(\left\{ {\begin{array}{*{20}{l}}{{n_{hh}} = {n_X} + {n_Y} = 0,05}\\{{n_{NaOH}} = 2{n_X} + {n_Y} = 0,06}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{n_X} = 0,01\,\,(mol)}\\{{n_Y} = 0,04\,\,(mol)}\end{array}} \right.\)
Bảo toàn khối lượng ta có :
\[\begin{array}{l}\begin{array}{*{20}{l}}{ \Rightarrow {\rm{ }}6,8{\rm{ }} + {\rm{ }}0,06.40{\rm{ }} = {\rm{ }}4,7{\rm{ }} + {\rm{ }}0,01.18{\rm{ }} + {\rm{ }}{m_{alcohol}}}\\{ \Rightarrow {m_{alcohol}}\; = {\rm{ }}4,32{\rm{ }}\left( {gam} \right)}\end{array}\\ \Rightarrow {M_{alcohol}}\; = \frac{{4,32}}{{0,04}}\; = 108\left( {g/mol} \right)\\ \Rightarrow alcohol{\rm{ }}l\`a {\rm{ }}{C_7}{H_8}O{\rm{ }}\left( {{C_6}{H_5}C{H_2}OH} \right)\end{array}\]
\( \Rightarrow \)ester Y là \[HCOOC{H_2}{C_6}{H_5}\] \( \Rightarrow \) muối tạo từ Y là HCOONa (0,04 mol)
Vì hỗn hợp muối thu được từ phản ứng là có 3 muối nên X + NaOH tạo 2 muối (không phải HCOONa) nên X là \[C{H_3}COO{C_6}{H_5}\] (0,01 mol)
Vậy muối gồm: HCOONa (0,04 mol), \[C{H_3}COONa\](0,01 mol) và \[{C_6}{H_5}ONa\](0,01 mol)
\( \Rightarrow {m_{C{H_3}COONa}} = 0,01.82 = 0,82\,gam\)
Đáp án: 0,82
Câu 141:
 Xem đáp án
Xem đáp án
Mô sinh trưởng ở thực vật bao gồm: mô phân sinh đỉnh, mô phân sinh lóng, mô phân sinh bên. Chọn A.
Câu 142:
 Xem đáp án
Xem đáp án
A. Sai. Thí nghiệm sử dụng hạt nảy mầm (chưa có khả năng quang hợp) nên vẫn có thể thành công trong điều kiện có ánh sáng.
B. Sai. Cường độ hô hấp ở hạt khô thấp, hạt nảy mầm có cường độ hô hấp cao nên thí nghiệm với hạt khô thì kết quả thí nghiệm sẽ thay đổi.
C. Sai. Dung dịch xút (NaOH) không tạo kết tủa với CO2.
D. Đúng. Quá trình hô hấp của thực vật thải ra CO2, CO2 tạo kết tủa với Ca(OH)2 làm nước vôi trong bị vẩn đục.
Chọn D.
Câu 143:
 Xem đáp án
Xem đáp án
Thể vàng chính là phần bao nang của trứng khi trứng chín, rụng và được giải phóng thì phần bao nang này trở thành thể vàng và được duy trì phát triển trong 7 ngày tiếp theo. Như vậy, trong một chu kì kinh nguyệt bình thường 28 ngày thì thể vàng được hình thành và phát triển ở giai đoạn ngày thứ 14 đến ngày thứ 21. Chọn C.
Câu 144:
 Xem đáp án
Xem đáp án
Trong số 64 loại bộ ba thì chỉ có 3 bộ ba làm nhiệm vụ kết thúc quá trình dịch mã, đó là các bộ ba 5’UAA3’ (3’AAU5’); 5’UAG3’ (3’GAU5’); 5’UGA3’ (3’AGU5’). Chọn B.
Câu 145:
 Xem đáp án
Xem đáp án
A. Sai. Vì đột biến cấu trúc nhiễm sắc thể có thể xảy sắc thể thường và ở nhiễm sắc thể giới tính.
B. Sai. Vì đột biến đảo đoạn chỉ xảy ra trong một NST nên không chuyển gen từ nhóm liên kết này sang nhóm liên kết khác.
C. Sai. Vì đột biến mất đoạn có thể làm mất một số gen nên làm thay đổi số lượng gen trên NST.
D. Đúng. Vì đối với đột biến chuyển đoạn trên một NST thì không làm thay đổi số lượng và thành phần gen của một NST.
Chọn D.
Câu 146:
 Xem đáp án
Xem đáp án
D. Sai. Vì phương pháp nuôi cấy mô là sử dụng phân bào nguyên phân (sinh sản vô tính) nên không tạo ra nguồn biến dị tổ hợp (biến dị tổ hợp chỉ được sinh ra thông qua sinh sản hữu tính). Chọn D.
Câu 147:
 Xem đáp án
Xem đáp án
Các yếu tố ngẫu nhiên tác động lên quần thể một cách ngẫu nhiên nên có thể loại bỏ hoàn toàn một alen có lợi ra khỏi quần thể. Chọn C.
Câu 148:
Những năm gần đây vùng Đồng bằng sông Cửu Long của nước ta thường xuyên bị nhiễm mặn do biến đổi khí hậu làm nước biển dâng. Nhằm tìm kiếm các loài thực vật phù hợp cho sản xuất, các nhà khoa học đã tiến hành các thử nghiệm trên hai loài thực vật đầm lầy (loài A và loài B) ở vùng này. Để nghiên cứu ảnh hưởng của nước biển tới hai loài này, chúng được trồng trong đầm nước mặn và đầm nước ngọt. Kết quả nghiên cứu được thể hiện ở sơ đồ dưới đây:
Khi nói về 2 loài này, có bao nhiêu phát biểu sau đây đúng?
I. Loài A chịu mặn tốt hơn loài B.
II. Trong cùng một độ mặn, loài B có sinh khối cao hơn loài A.
III. Trong tương lai nước biển dâng loài A sẽ trở nên phổ biến hơn loài B.
IV. Cả 2 loài A và B đều là sinh trưởng tốt trong điều kiện nước ngọt.
 Xem đáp án
Xem đáp án
I. Đúng. Vì loài A chịu mặn tốt hơn loài B. Trong giới hạn độ muối 60% - 80%, loài A vẫn còn sinh trưởng mặc dù sinh khối thấp hơn, trong khi đó loài B bị chết.
II. Sai. Vì trong cùng một độ mặn, loài B có sinh khối thấp hơn loài A.
III. Đúng. Nhờ khả năng chịu mặn tốt hơn loài B nên nếu trong tương lai nước biển dâng, độ mặn tăng lên thì loài A sẽ trở lên phổ biến hơn.
IV. Đúng. Cả 2 loài sinh trưởng tốt hơn trong điều kiện nước ngọt.
Chọn A.
Câu 149:
Xét quần thể một loài thực vật giao phấn đang ở trạng thái cân bằng di truyền, xét 1 gen có hai alen. Alen A quy định hoa đỏ trội hoàn toàn so với alen a quy định hoa trắng. Theo định luật Hacđi - Vanbec, có bao nhiêu quần thể sau đây đang cân bằng về mặt di truyền?
I. Quần thể có 100% cây hoa trắng.
II. Quần thể có 100% cây hoa đỏ mang kiểu gen AA.
III. Quần thể có tần số các kiểu gen lần lượt là: 0,64AA : 0,32Aa : 0,04aa.
IV. Quần thể có tần số các kiểu gen lần lượt là: 0,5AA : 0,5Aa.
 Xem đáp án
Xem đáp án
Quần thể cân bằng về mặt di truyền khi cấu trúc của quần thể tuân theo định luật Hacđi – Vanbec có dạng: p2 + 2pq + q2 (p và q là lần lượt là tần số alen A và a). Như vậy, quần thể cân bằng di truyền bao gồm I, II, III. Chọn C.
Câu 150:
Ở ruồi giấm, alen A quy định thân xám trội hoàn toàn so với alen a quy định thân đen; alen B quy định cánh dài trội hoàn toàn so với alen b quy định cánh cụt; 2 cặp gen này nằm trên NST thường; alen D quy định mắt đỏ trội hoàn toàn so với alen d quy định mắt trắng, cặp gen này nằm ở vùng không tương đồng trên NST giới tính X. Phép lai P dị hợp 3 cặp gen: Ruồi thân xám, cánh dài, mắt đỏ × Ruồi thân xám, cánh dài, mắt đỏ, thu được F1 có 17,5% ruồi thân xám, cánh dài, mắt trắng. Theo lí thuyết, trong tổng số ruồi cái thân xám, cánh dài, mắt đỏ ở F1, số ruồi không thuần chủng chiếm tỉ lệ là bao nhiêu?
 Xem đáp án
Xem đáp án
Ruồi mắt đỏ × Ruồi mắt đỏ thu được đời con có ruồi mắt trắng → P: XDXd × XDY → F1: 1XDXD : 1XDXd : 1XDY : 1XdY.
F1 có 17,5% ruồi thân xám, cánh dài, mắt trắng (A-B-XdY) → A-B- = 17,5% : 25% = 0,7.
Ở ruồi giấm, hoán vị gen chỉ xảy ra ở bên con cái →
Tỉ lệ ruồi cái thân xám, cánh dài, mắt đỏ ở F1 là: A-B-XDX- = 0,7 × 0,5 = 0,35.
Tỉ lệ ruồi cái thân xám, cánh dài, mắt đỏ thuần chủng ở F1 là:
→ Trong trong tổng số ruồi cái thân xám, cánh dài, mắt đỏ ở F1, số ruồi không thuần chủng chiếm tỉ lệ:![]()
. Đáp án:![]()
.