Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 9)
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 9)
-
90 lượt thi
-
150 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
PHẦN 1: TƯ DUY ĐỊNH LƯỢNG
Lĩnh vực: Toán học (50 câu – 75 phút)
Câu 1. Mọi người lấy thông tin y tế của họ ở đâu?
|
Nguồn |
Phần trăm những người được khảo sát |
|
Bác sĩ |
\(63\% \)
|
|
Internet |
\(13\% \)
|
|
Tạp chí hoặc tờ rơi |
\(9\% \)
|
|
Nhà thuốc |
\(6\% \)
|
|
Tivi |
\(2\% \)
|
|
Khác hoặc không có cái nào ở trên |
\(7\% \)
|
Bảng trên hiển thị tóm tắt 1200 câu trả lời cho một câu hỏi khảo sát. Dựa trên bảng, có bao nhiêu người trong số những người được khảo sát nhận được hầu hết thông tin y tế của họ từ bác sĩ hoặc Internet?
 Xem đáp án
Xem đáp án
Phần trăm những người được khảo sát từ bác sĩ hoặc Internet là \(76\% \).
Do đó, số người được khảo sát cần tính là \(1\,\,200 \cdot 76\% = 912\) (người). Chọn C.
Câu 2:
Trong không gian Oxyz, cho hai điểm \[A\left( { - 2\,;\,\,3\,;\,\,4} \right),\,\,B\left( {8\,;\,\, - 5\,;\,\,6} \right).\] Hình chiếu vuông góc của trung điểm \[I\] của đoạn AB trên mặt phẳng \(\left( {Oyz} \right)\) là điểm nào dưới đây?
 Xem đáp án
Xem đáp án
Vì \(I\) là trung điểm của đoạn AB nên \(I\left( {3\,;\,\, - 1\,;\,\,5} \right).\)
Khi đó hình chiếu của \(I\) lên \(\left( {Oyz} \right)\) là \(M\left( {0\,;\,\, - 1\,;\,\,5} \right).\) Chọn B.
Câu 3:
Cho số phức \(z\) thỏa mãn \(\left( {2 + i} \right)\bar z + 1 - 5i = 0.\) Tính \(\left| {z + 1 - i} \right|.\)
 Xem đáp án
Xem đáp án
Ta có: \(\left( {2 + i} \right)\bar z + 1 - 5i = 0 \Rightarrow \bar z = \frac{{ - 1 + 5i}}{{2 + i}} = \frac{3}{5} + \frac{{11}}{5}i\)\( \Rightarrow z + 1 + i = \left( {\frac{3}{5} - \frac{{11}}{5}i} \right) + 1 + i = \frac{8}{5} - \frac{6}{5}i{\rm{.}}\)
Do đó \(\left| {z + 1 - i} \right| = 2\). Chọn B.
Câu 4:
Một vật chuyển động theo phương trình \(s\left( t \right) = \frac{1}{3}{t^3} - 2{t^2} + 4t\) với \(t\) (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \[s\] (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Sau bao lâu thì chuyển động dừng lại?
 Xem đáp án
Xem đáp án
Ta có \(v\left( t \right) = s'\left( t \right) = {t^2} - 4t + 4\,\,(\;{\rm{m}}/{\rm{s}}).\)
Chuyển động dừng lại nên \(v\left( t \right) = 0 \Leftrightarrow {t^2} - 4t + 4 \Leftrightarrow t = 2\) (giây).
Vậy sau 2 giây thì chuyển động dừng lại. Chọn A.
Câu 5:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a, cạnh bên SA vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BD bằng
 Xem đáp án
Xem đáp án
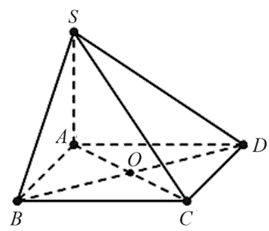
Gọi \(O\) là tâm của hình vuông \[ABCD,\] ta có \(AO \bot BD.\)
Mặt khác \(SA \bot (ABCD) \Rightarrow SA \bot AO.\)
Nên \[AO\] là đoạn vuông góc chung của hai đường thẳng \[SA\] và \[BD.\]
Do đó \[d\left( {SA\,;\,\,BD} \right) = AO = \frac{1}{2}AC = a\sqrt 2 \]. Chọn A.Câu 6:
Trong không gian \[Oxyz,\] cho ba điểm \[A\left( {1\,;\,\,1\,;\,\,0} \right),\,\,B\left( {0\,;\,\,1\,;\,\,0} \right),\,\,C\left( { - 1\,;\,\,0\,;\,\,2} \right).\] Đường thẳng \(d\) vuông góc với mặt phẳng \(\left( {ABC} \right).\) Vectơ nào dưới đây là một vectơ chỉ phương của \(d\)?
 Xem đáp án
Xem đáp án
Ta có \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AB} = \left( { - 1\,;\,\,0\,;\,\,0} \right)}\\{\overrightarrow {AC} = \left( { - 2\,;\,\, - 1\,;\,\,2} \right)}\end{array}} \right. \Rightarrow \left[ {\overrightarrow {AB} \,;\,\,\overrightarrow {AC} } \right] = \left( {0\,;\,\,2\,;\,\,1} \right).\)
Suy ra \(\left( {0\,;\,\,2\,;\,\,1} \right)\) là vectơ chỉ phương của đường thẳng \[d.\] Chọn A.
Câu 7:
Cho đường thẳng \(\Delta \) có phương trình \(y = 2x + 1\) cắt đồ thị của hàm số \(y = {x^3} - x + 3\) tại hai điểm \(A\) và \(B\) được kí hiệu lần lượt là \(A\left( {{x_A}\,;\,\,{y_A}} \right)\) và \(B\left( {{x_B}\,;\,\,{y_B}} \right)\) trong đó \({x_B} < {x_A}.\) Tính \({x_B} + {y_B}.\)
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của \(\Delta \) và \(y = {x^3} - x + 3\):
\({x^3} - x + 3 = 2x + 1 \Leftrightarrow {x^3} - 3x + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2 \Rightarrow y = - 3}\\{x = 1 \Rightarrow y = 3}\end{array}} \right.\).
Vậy \(A\left( {1\,;\,\,3} \right)\,,\,\,B\left( { - 2\,;\,\, - 3} \right) \Rightarrow {x_B} + {y_B} = - 5\). Chọn A.
Câu 8:
Cho lăng trụ đứng tam giác có độ dài các cạnh đáy là \(37\,\;{\rm{cm}}\,,\,\,3\,\;{\rm{cm}}\,,\,\,30\;\,\;{\rm{cm}}\) và biết tổng diện tích các mặt bên là \(480\;\,{\rm{c}}{{\rm{m}}^2}.\) Thể tích \[V\] của lăng trụ đó là
 Xem đáp án
Xem đáp án
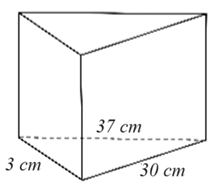
Nửa chu vi đáy là: \[p = \frac{{37 + 13 + 30}}{2} = 40\,\,(cm).\]
Diện tích đáy của hình lăng trụ là:
\(S = \sqrt {40 \cdot \left( {40 - 37} \right) \cdot \left( {40 - 13} \right) \cdot \left( {40 - 30} \right)} = 180\,\,\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Gọi \(x\) là độ dài chiều cao của lăng trụ.
Vì các mặt bên của hình lăng trụ đứng là hình chữ nhật nên \({S_{xq}} = 13x + 37x + 30x = 480 \Rightarrow x = 6\).Vậy thể tích của lăng trụ là: \(V = 6 \cdot 180 = 1080\;\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\) Chọn D.
Câu 9:
Cho hàm số \(f\left( x \right)\) có \(f\left( { - 1} \right) < 0\) và đạo hàm \(f'\left( x \right) = \left( {{x^2} - 2x - 3} \right)\left( {x + 1} \right)\) với mọi \(x \in \mathbb{R}.\) Số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và trục hoành là
 Xem đáp án
Xem đáp án
Xét phương trình \(f'\left( x \right) = 0 \Rightarrow \left( {{x^2} - 2x - 3} \right)\left( {x + 1} \right) \Leftrightarrow \left( {x - 3} \right){\left( {x + 1} \right)^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 3}\end{array}} \right..\)
Từ đó ta có bảng biến thiên hàm số \(f\left( x \right)\) như sau:
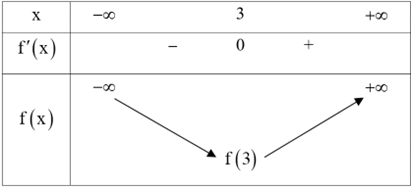
Vì \(0 > f\left( { - 1} \right) > f\left( 3 \right)\) nên đường thẳng \(y = 0\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm phân biệt.
Vậy số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và trục hoành là 2. Chọn B.
Câu 10:
Trong không gian \[Oxyz,\] cho đường thẳng \(d:\frac{{x - 1}}{3} = \frac{{y + 1}}{1} = \frac{z}{1}\) và mặt phẳng \(\left( P \right):2x + y - 2z + 2 = 0.\) Phương trình mặt cầu \(\left( S \right)\) có tâm nằm trên đường thẳng \(d\) có bán kính nhỏ nhất tiếp xúc với \(\left( P \right)\) và đi qua điểm \(A\left( {1\,;\,\, - 1\,;\,\,1} \right)\) là
 Xem đáp án
Xem đáp án
Gọi \(I\) là tâm của \(\left( S \right)\)
Vì \[I \in d\] nên \[I\left( {1 + 3t\,;\,\, - 1 + t\,;\,\,t} \right).\] Bán kính \(R = IA = \sqrt {11{t^2} - 2t + 1} .\)
Mặt phẳng \(\left( P \right)\) tiếp xúc với \(\left( S \right)\) nên \(d\left( {I,\,\,\left( P \right)} \right) = \frac{{\left| {5t + 3} \right|}}{3} = R.\)
\( \Leftrightarrow 37{t^2} - 24t = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 0 \Rightarrow R = 1}\\{t = \frac{{24}}{{37}} \Rightarrow R = \frac{{77}}{{37}}}\end{array}} \right.\).
Vì \(\left( S \right)\) có bán kính nhỏ nhất nên chọn \(t = 0\,,\,\,R = 1.\) Suy ra \[I\left( {1\,;\,\, - 1\,;\,\,0} \right).\]
Vậy phương trình mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 1.\) Chọn C.
Câu 11:
Gọi \({m_1},\,\,{m_2}\) là hai giá trị khác nhau của tham số \(m\) để phương trình \({x^2} - 3x + {m^2} - 3m + 4 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) thoả mãn \({x_1} = 2{x_2}.\) Giá trị của biểu thức \({m_1} + {m_2} + {m_1}{m_2}\) là
 Xem đáp án
Xem đáp án
Vì phương trình có hai nghiệm \({x_1}\,,\,\,{x_2}\) thỏa mãn \({x_1} = 2{x_2}\).
Từ định lí Viète suy ra \(3 = {x_1} + {x_2} = 3{x_2} \Rightarrow {x_2} = 1.\)
Thay \({x_2} = 1\) vào phương trình ta được: \(1 - 3 + {m^2} - 3m + 4 = 0\)\( \Leftrightarrow {m^2} - 3m + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m_1} = 1}\\{{m_2} = 2}\end{array}} \right..\)
Ta có \(\Delta = 9 - 4{m^2} + 12m - 16 = - 4{m^2} + 12m - 7\).
Nên \({m_1} = 1\,;\,\,{m_2} = 2\) thỏa mãn điều kiện \(\Delta > 0\) để phương trình có hai nghiệm phân biệt.
Chọn C.
Câu 12:
Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2019\,;\,\,2019} \right]\) để hàm số \(y = \ln \left( {{x^2} + 2} \right) - mx + 1\) đồng biến trên \(\mathbb{R}\)?
 Xem đáp án
Xem đáp án
Ta có \(y' = \frac{{2x}}{{{x^2} + 2}} - m.\)
Hàm số đã cho đồng biến trên \(\mathbb{R} \Leftrightarrow \frac{{2x}}{{{x^2} + 2}} - m \ge 0\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow m \le \frac{{2x}}{{{x^2} + 2}}\,\,\forall x \in \mathbb{R}\).
Xét \(h\left( x \right) = \frac{{2x}}{{{x^2} + 2}}\,\,\forall x \in \mathbb{R}\), có \(h'\left( x \right) = \frac{{4 - 2{x^2}}}{{{{\left( {{x^2} + 2} \right)}^2}}}\)
Bảng biến thiên:
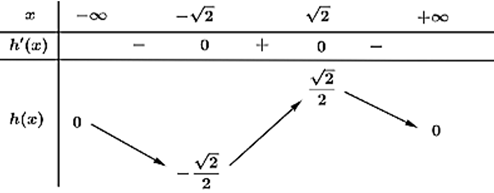
Suy ra \(m \le - \frac{{\sqrt 2 }}{2}\) và \(m\) là số nguyên trong đoạn \(\left[ { - 2019\,;\,\,2019} \right]\) nên có 2019 số. Chọn A.
Câu 13:
Người ta trồng cây theo hình tam giác với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ở hàng thứ ba có 3 cây, ..., ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4 950 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
 Xem đáp án
Xem đáp án
Tổng số cây trồng hết là \(1 + 2 + 3 + \ldots + n = 4950.\)
Dễ thấy \({S_n} = 1 + 2 + 3 + \ldots + n\) là tổng của CSC với \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{d = 1}\end{array}} \right..\)
Do đó \({S_n} = \frac{{n\left( {n + 1} \right)}}{2}\) suy ra \(\frac{{n\left( {n + 1} \right)}}{2} = 4950 \Leftrightarrow n = 99.\) Chọn B.
Câu 14:
Bất phương trình \(\left( {{x^3} - 9x} \right)\ln \left( {x + 5} \right) \le 0\) có bao nhiêu nghiệm nguyên?
 Xem đáp án
Xem đáp án
Điều kiện: \(x > - 5.\)
Cho \(\left( {{x^3} - 9x} \right)\ln \left( {x + 5} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^3} - 9x = 0}\\{\ln \left( {x + 5} \right) = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 3}\\{x = 0}\\{x = 3}\\{x = - 4}\end{array}} \right.} \right.\).
Bảng xét dấu:
![]()
Dựa vào bảng xét dấu ta thấy \(f\left( x \right) \le 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 4 \le x \le - 3}\\{0 \le x \le 3}\end{array}} \right.\)
Vì \(x \in \mathbb{Z}\) nên \[x \in \left\{ { - 4\,;\,\, - 3\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3} \right\}\].
Vậy có 6 giá trị nguyên của \(x\) thỏa mãn bài toán. Chọn C.
Câu 15:
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f'\left( x \right) = \left( {x + 1} \right){e^x},\,\,f\left( 0 \right) = 0\) và \(\int {f\left( x \right)} \,{\rm{d}}x = \left( {ax + b} \right){e^x} + c\) với \[a,\,\,b,\,\,c\] là các hằng số. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Theo đề: \(f'\left( x \right) = \left( {x + 1} \right){e^x}\). Nguyên hàm 2 vế ta được
\(\int {f'\left( x \right)} \,dx = \int {\left( {x + 1} \right){e^x}} \,dx \Leftrightarrow f\left( x \right) = \left( {x + 1} \right){e^x} - \int {{e^x}} dx\)
\( \Rightarrow f\left( x \right) = \left( {x + 1} \right){e^x} - {e^x} + C = x{e^x} + C\).
Mà \(f\left( 0 \right) = 0 \Rightarrow 0 \cdot {e^0} + C = 0 \Leftrightarrow C = 0 \Rightarrow f\left( x \right) = x{e^x}\)
\( \Rightarrow \int f \left( x \right)dx = \int x {e^x}dx = x{e^x} - \int {{e^x}} dx = x{e^x} - {e^x} + C = \left( {x - 1} \right){e^x} + C.\)
Suy ra \(a = 1\,;\,\,b = - 1 \Rightarrow a + b = 0.\) Chọn D.
Câu 16:
Cho hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{m^2}6 \ge 6 - x}\\{3x - 1 \le x + 5}\end{array}} \right.\). Tất cả các giá trị của tham số \(m\) để hệ bất phương trình đã cho có nghiệm duy nhất là
 Xem đáp án
Xem đáp án
Bất phương trình \({m^2}x \ge 6 - x \Leftrightarrow \left( {{m^2} + 1} \right)x \ge 6\)\( \Leftrightarrow x \ge \frac{6}{{{m^2} + 1}} \Rightarrow {s_1} = \left[ {\frac{6}{{{m^2} + 1}};\,\, + \infty } \right){\rm{. }}\)
Bất phương trình \(3x - 1 \le x + 5 \Leftrightarrow x \le 3 \Leftrightarrow {s_2} = \left( { - \infty \,;\,\,3} \right].\)
Để hệ bất phương trình có nghiệm duy nhất \( \Leftrightarrow {s_1} \cap {s_2}\) là tập hợp có đúng một phần tử
\( \Leftrightarrow \frac{6}{{{m^2} + 1}} = 3 \Leftrightarrow {m^2} = 1 \Leftrightarrow m = \pm 1.\) Chọn C.
Câu 17:
Giả sử một vật dao động điều hòa xung quanh vị trí cân băng theo phương trình \(x = 2\sin \left( {5t - \frac{\pi }{6}} \right).\) Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimet. Vật đi qua vị trí cân bằng bao nhiêu lần trong 3 giây đầu?
 Xem đáp án
Xem đáp án
Vật qua vị trí cân bằng khi \(x = 0\), khi đó ta có:
\(2\sin \left( {5t - \frac{\pi }{6}} \right) = 0 \Leftrightarrow 5t - \frac{\pi }{6} = k\pi \Leftrightarrow t = \frac{\pi }{{30}} + \frac{{k\pi }}{5}.\)
Mà \(0 \le t \le 3 \Leftrightarrow 0 \le \frac{\pi }{{30}} + \frac{{k\pi }}{5} \le 3 \Leftrightarrow 0,17 \le k \le 4,61.\)
Vì \(k \in \mathbb{Z}\) nên \(k \in \left\{ {0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4} \right\}.\)
Vậy vật đi qua vị trí cân bằng 5 lần. Chọn A.
Câu 18:
Gọi \({z_1},\,\,{z_2}\) là hai nghiệm phức của phương trình \(\left( {z - i} \right)\left( {z + i} \right) = 2\left( {z - 3} \right).\) Giá trị của \(z_1^2 + z_2^2\) bằng
 Xem đáp án
Xem đáp án
Ta có \(\left( {z - i} \right)\left( {z + i} \right) = 2\left( {z - 3} \right) \Leftrightarrow {z^2} - {i^2} = 2z - 6\)
\( \Leftrightarrow {z^2} - 2z + 7 = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{z_1} + {z_2} = \frac{{ - b}}{a} = 2}\\{{z_1}{z_2} = \frac{c}{a} = 7}\end{array}} \right.{\rm{. }}\)
Khi đó \(z_1^2 + z_2^2 = {\left( {{z_1} + {z_2}} \right)^2} - 2{z_1}{z_2} = {2^2} - 2.7 = - 10.\) Chọn D.
Câu 19:
Có bao nhiêu tiếp tuyến của đồ thị hàm số \(y = \frac{{2x - 3}}{{x + 2}}\) đi qua giao điểm của hai đường tiệm cận của đồ thị hàm số đó?
 Xem đáp án
Xem đáp án
Đồ thị hàm số nhận đường thẳng \(x = - \frac{d}{c} = - 2\) làm tiệm cận đứng.
Đồ thị hàm số nhận đường thẳng \(y = \frac{a}{c} = 2\) làm tiệm cận ngang.
Do đó \(I\left( { - 2\,;\,\,2} \right)\) là giao điểm của hai đường tiệm cận. Ta có \(y' = \frac{7}{{{{\left( {x + 2} \right)}^2}}}\).
Gọi tiếp tuyến tại \(M\left( {{x_0}\,;\,\,{y_0}} \right)\) của đồ thị hàm số \(y = \frac{{2x - 3}}{{x + 2}}\) có dạng: \(\Delta :y = {y^\prime }\left( {{x_0}} \right) \cdot \left( {x - {x_0}} \right) + {y_0}\) hay \(\Delta :y = \frac{7}{{{{\left( {{x_0} + 2} \right)}^2}}} \cdot \left( {x - {x_0}} \right) + \frac{{2{x_0} - 3}}{{{x_0} + 2}}\).
Vì \(\Delta \) đi qua \(I\left( { - 2\,;\,\,2} \right)\) nên \(2 = \frac{7}{{{{\left( {{x_0} + 2} \right)}^2}}} \cdot \left( { - 2 - {x_0}} \right) + \frac{{2{x_0} - 3}}{{{x_0} + 2}}\)
\( \Leftrightarrow 2 = \frac{{ - 7}}{{{{\left( {{x_0} + 2} \right)}^2}}} \cdot \left( {{x_0} + 2} \right) + \frac{{2{x_0} - 3}}{{{x_0} + 2}} \Leftrightarrow 2 = \frac{{ - 7}}{{\left( {{x_0} + 2} \right)}} + \frac{{2{x_0} - 3}}{{{x_0} + 2}}\)
\( \Leftrightarrow 2 = \frac{{2{x_0} - 10}}{{{x_0} + 2}} \Leftrightarrow 4 = - 10 \Rightarrow \) Phương trình vô nghiệm.
Vậy không tồn tại tiếp tuyến nào thỏa mãn bài toán. Chọn B.
Câu 20:
Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 mét so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v\left( t \right) = 10t - {t^2}\), trong đó \(t\) (phút) là thời gian tính từ lúc bắt đầu chuyển động, \(v\left( t \right)\) được tính theo đơn vị mét/phút \(\left( {{\rm{m}}/{\rm{p}}} \right)\). Nếu như vậy thì khi bắt đầu tiếp xúc đất vận tốc \(v\) của khí cầu là
 Xem đáp án
Xem đáp án
Gọi thời điểm khinh khí cầu bắt đầu chuyển động là \(t = 0\)
Thời điểm khinh khí cầu bắt đầu tiếp đất là \({t_1}.\)
Do đó quãng đường khinh khí cầu đi được từ lúc bắt đầu đến khi chạm đất là \({S_1}.\)
Ta có \({S_1} = \int\limits_0^{{t_1}} {\left( {10t - {t^2}} \right){\rm{d}}t} = 5t_1^2 - \frac{{t_1^3}}{3} = 162 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{t_1} = - 4,93}\\{{t_1} = 10,93}\\{{t_2} = 9}\end{array}} \right..\)
Do \(v\left( t \right) \ge 0\) nên \(t \in \left[ {0\,;\,\,10} \right]\) suy ra \(t = 9\) giây.
Vậy khi bắt đầu tiếp đất thì vận tốc của khí cầu là \(v\left( 9 \right) = 9\) (mét/phút). Chọn C.
Câu 21:
Cho hình trụ có chiều cao bằng \(6\sqrt 2 \;\,{\rm{cm}}.\) Biết rằng một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song \(AB\,,\,\,A'B'\) mà \(AB = A'B' = 6\;\,{\rm{cm}}\), diện tích tứ giác \(ABB'A'\) bằng \(60\,\;{\rm{c}}{{\rm{m}}^{2.}}.\) Bán kính đáy của hình trụ bằng
 Xem đáp án
Xem đáp án
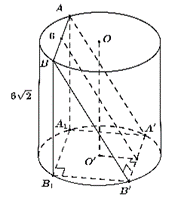
Gọi \(O,\,\,O'\) là tâm các đáy hình trụ (hình vẽ).
Vì \(AB = A'B'\) nên \(\left( {ABB'A'} \right)\) đi qua trung điểm của đoạn \(OO'\) và \(ABB'A'\) là hình chữ nhật.
Ta có \({S_{ABB'A'}} = AB \cdot AA' \Leftrightarrow 60 = 6 \cdot AA' \Rightarrow AA' = 10\,\,(\;{\rm{cm}}).\)
Gọi \({A_1},\,\,{B_1}\) lần lượt là hình chiếu của \[A,\,\,B\] trên mặt đáy chứa \(A'\) và \(B'\). Do đó \[A'B'{B_1}{A_1}\] là hình chữ nhật có \(A'B' = 6\,\,\;{\rm{cm}}\,{\rm{;}}\)
\({B_1}B' = \sqrt {B{{B'}^2} - BB_1^2} = \sqrt {{{10}^2} - {{\left( {6\sqrt 2 } \right)}^2}} = 2\sqrt 7 \,\,(\;{\rm{cm}})\).Gọi \(R\) là bán kính đáy của hình trụ.
Ta có \(2R = A'{B_1} = \sqrt {{B_1}{{B'}^2} + A'{{B'}^2}} = 8 \Rightarrow R = 4\,\,(\;{\rm{cm}})\). Chọn C.
Câu 22:
Tìm giá trị thực của tham số \(m\) để hàm số \(y = \left( {m - 1} \right){x^4} - \left( {{m^2} - 2} \right){x^2} + 1\) đạt cực tiểu tại \(x = - 1.\)
 Xem đáp án
Xem đáp án
Tập xác định: \(D = \mathbb{R}.\)
Ta có \(y' = 4\left( {m - 1} \right){x^3} - 2\left( {{m^2} - 2} \right)x\).
Hàm số đạt cực tiểu tại \(x = - 1 \Rightarrow y'\left( { - 1} \right) = 0 \Leftrightarrow - \,4\left( {m - 1} \right) + 2\left( {{m^2} - 2} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 0}\\{m = 2}\end{array}} \right.\).
• Với \(m = 0\), hàm số trở thành \(y = - {x^4} + 2{x^2} + 2019.\) Dễ thấy hàm số đạt cực đại tại \(x = - 1\)
• Với \(m = 2\), hàm số trở thành \(y = {x^4} - 2{x^2} + 2019.\) Dễ thấy hàm số đạt cực tiểu tại \(x = - 1\).
• Với \(m = 2\) thì hàm số \(y = \left( {m - 1} \right){x^4} - \left( {m - 2} \right){x^2} + 2019\) đạt cực tiểu tại \(x = - 1\).
Chọn D.
Câu 23:
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \(a,\) cạnh bên \[SA\] vuông góc với mă̆t phẳng đáy, \(SA = a\sqrt 2 .\) Gọi \[M,\,\,N\] lần lượt là hình chiếu vuông góc của điểm \(A\) trên các cạnh \[SB,\,\,SD.\] Góc giữa mặt phẳng \[\left( {AMN} \right)\] và đường thẳng \[SB\] bằng
 Xem đáp án
Xem đáp án
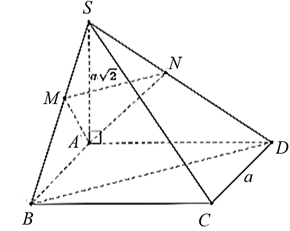
Ta có \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM\)
\( \Rightarrow AM \bot \left( {SBC} \right) \Rightarrow AM \bot SC.\)
Tương tự ta cũng có \(AN \bot SC \Rightarrow \left( {AMN} \right) \bot SC.\)
Gọi \(\varphi \) là góc giữa đường thẳng SB và \(\left( {AMN} \right)\)
Chuẩn hóa và chọn hệ trục tọa độ sao cho\(D\left( {1\,;\,\,0\,;\,\,0} \right),\,\,S\left( {0\,;\,\,0\,;\,\,\sqrt 2 } \right),\,\,C\left( {1\,;\,\,1\,;\,\,0} \right),\)\(A\left( {0\,;\,\,0\,;\,\,0} \right),\,\,\)\(B\left( {0\,;\,\,1\,;\,\,0} \right),\,\,\)\(\overrightarrow {SC} = \left( {1\,;\,\,1\,;\,\, - \sqrt 2 } \right),\,\,\overrightarrow {SB} = \left( {0\,;\,\,1\,;\,\, - \sqrt 2 } \right).\)
Do \(\left( {AMN} \right) \bot SC\) nên \(\left( {AMN} \right)\) có VTPT \(\overrightarrow {SC} .\)
Do đó \(\sin \varphi = \frac{{\left| 3 \right|}}{{2\sqrt 3 }} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = 60^\circ {\rm{. }}\)Chọn D.
Câu 24:
Trong không gian \[Oxyz,\] cho hai điểm \(A\left( { - 2\,;\,\,3\,;\,\,1} \right)\) và \(B\left( {5\,;\,\,6\,;\,\,2} \right).\) Đường thẳng \[AB\] cắt mặt phẳng \(\left( {Oxz} \right)\) tại điểm \[M.\] Tính tỉ số \(\frac{{AM}}{{BM}}.\)
 Xem đáp án
Xem đáp án
\(M \in \left( {Oxz} \right) \Rightarrow M\left( {x\,;\,\,0\,;\,\,z} \right)\,;\,\,\overrightarrow {AB} = \left( {7\,;\,\,3\,;\,\,1} \right) \Rightarrow AB = \sqrt {59} \,;\,\,\overrightarrow {AM} = \left( {x + 2\,;\,\, - 3\,;\,\,z - 1} \right)\) và \[A,\,\,B,\,\,M\] thẳng hàng
\( \Rightarrow \overrightarrow {AM} = k \cdot \overrightarrow {AB} (k \in \mathbb{R}) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x + 2 = 7k}\\{ - 3 = 3k}\\{z - 1 = k}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 9}\\{ - 1 = k \Rightarrow M\left( { - 9\,;\,\,0\,;\,\,0} \right)}\\{z = 0}\end{array}} \right.} \right.\) \(\overrightarrow {BM} = \left( { - 14\,;\,\, - 6\,;\,\, - 2} \right)\,;\,\,\overrightarrow {AM} = \left( { - 7\,;\,\, - 3\,;\,\, - 1} \right) \Rightarrow BM = 2AM.\) Chọn A.
Câu 25:
Trên mặt phẳng toạ độ \[Oxy,\] đường thẳng \(12x + 5y = 60\) tạo với hai trục tọa độ một tam giác. Tổng độ dài các đường cao của tam giác đó là
 Xem đáp án
Xem đáp án
Gọi \[A,\,\,B\] lần lượt là giao điểm của đường thẳng đã cho với Ox, Oy.
Ta có \(12x + 5y = 60 \Leftrightarrow \frac{x}{5} + \frac{y}{{12}} = 0.\) Do đó \(A\left( {5\,;\,\,0} \right)\,,\,\,B\left( {0\,;\,\,12} \right)\).
Gọi \(H\) là hình chiếu của \(O\) lên AB. Khi đó: \(OH = d\left( {O\,;\,\,AB} \right) = \frac{{\left| {12 \cdot 0 + 5 \cdot 0 - 60} \right|}}{{\sqrt {{{12}^2} + {5^2}} }} = \frac{{60}}{{13}}.\)
Tam giác OAB là tam giác vuông tại O nên tổng độ dài các đường cao là
\(OA + OB + OH = 5 + 12 + \frac{{60}}{{13}} = \frac{{281}}{{13}}.\) Chọn B.
Câu 26:
Cho hình thang \[ABCD\] có \[AB\] song song \[CD\] và \(AB = AD = BC = a\,,\,\,CD = 2a.\) Thể tích của khối tròn xoay khi quay hình thang \[ABCD\] quanh trục \[AB\] bằng
 Xem đáp án
Xem đáp án
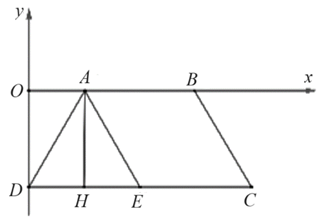
Cách 1: Dễ thấy \[ABCE\] là hình bình hành nên \(AE = BC = a.\)
Do đó \[ADE\] là tam giác đều có \(AH = \frac{{a\sqrt 3 }}{2}.\)
Xét hệ trục tọa độ \[Oxy\] (như hình vẽ) có
Phương trình \(CD:y = - \frac{{a\sqrt 3 }}{2};\)
\[{x_D} = 0\,;\,\,{x_C} = 2a\,;\,\,A\left( {\frac{a}{2}\,;\,\,0} \right).\]
Phương trình \(AD:y = \sqrt 3 x - \frac{{a\sqrt 3 }}{2}\)
Do đó \[V = \pi \int\limits_0^{2a} {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} - 2\pi \int\limits_0^{\frac{a}{2}} {{{\left( {\sqrt 3 x - \frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{{3\pi {a^2}}}{4} \cdot 2a - 2\pi \int\limits_0^{\frac{a}{2}} {\left( {3{x^2} - 3ax - \frac{{3{a^2}}}{4}} \right)} \]
\( = \frac{{3\pi {a^3}}}{2} - \left. {2\pi \left( {{x^3} - \frac{{3a}}{2}{x^2} + \frac{{3{a^2}}}{4}x} \right)} \right|_0^{\frac{a}{2}} = \frac{{3\pi {a^3}}}{2} - 2\pi \cdot \frac{{{a^3}}}{8} = \frac{5}{4}\pi {a^3}\).
Cách 2: Thể tích khối tròn xoay được tạo ra theo đề bài là thể tích cho khối trụ có chiều cao \[2a\] bán kính đáy bằng \(\frac{{a\sqrt 3 }}{2}\) trừ đi thể tích hai khối nón có cùng chiều cao bằng \(\frac{a}{2}\) và bán kính đáy bằng \(\frac{{a\sqrt 3 }}{2}.\)
Do đó \(V = \pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2}2a - 2 \cdot \frac{1}{3}\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} \cdot \frac{a}{2} = \frac{5}{4}\pi {a^3}\). Chọn A.
Câu 27:
Cho \[x,\,\,y\] thỏa mãn \(x + y = 2.\) Giá trị nhỏ nhất của \[A = 2 \cdot {3^y} + \frac{1}{{24}} \cdot {3^{2x}}\] là
 Xem đáp án
Xem đáp án
Ta có: \(x + y = 2 \Leftrightarrow y = 2 - x\)
Xét \(A = 2 \cdot {3^y} + \frac{1}{{24}} \cdot {3^{2x}} = 2 \cdot {3^{2 - x}} + \frac{1}{{24}} \cdot {3^{2x}} = \frac{{18}}{{{3^x}}} + \frac{1}{{24}} \cdot {\left( {{3^x}} \right)^2}.\)
Đặt \(t = {3^x},t > 0\), khi đó \(A = \frac{{18}}{t} + \frac{{{t^2}}}{{24}}.\)
Xét \(A' = \frac{t}{{12}} - \frac{{18}}{{{t^2}}} = 0 \Leftrightarrow t = 6.\)
Bảng biến thiên của hàm số \(A = \frac{{18}}{t} + \frac{{{t^2}}}{{24}}\;\,\forall t \in \left( {0\,;\,\, + \infty } \right).\)
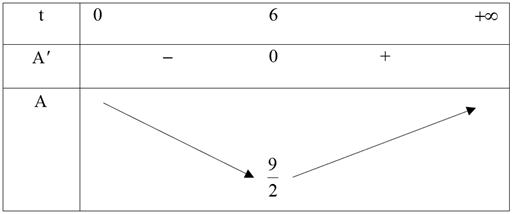
Khi đó \(A\) đạt giá trị nhỏ nhất tại \(t = 6 \Rightarrow {A_{\min }} = \frac{9}{2}.\) Chọn C.
Câu 28:
Cho tứ diện \[ABCD\] có \[AB,\,\,AC,\,\,AD\] đôi một vuông góc với nhau và \(AB = AC = AD = 2a.\) Gọi \(E\) và \(F\) lần lượt là trung điểm của \[BC,\,\,BD.\] Thể tích của khối chóp \[A.EFDC\] bằng
 Xem đáp án
Xem đáp án
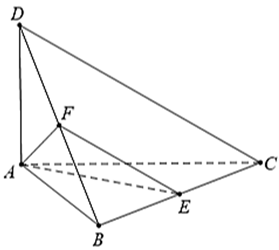
Thể tích khối tứ diện \[ABCD\] là:
\({V_{ABCD}} = \frac{1}{3}AD \cdot {S_{ABC}} = \frac{1}{6}AD.AB \cdot AC = \frac{4}{3}{a^3}.\)
Ta có \(\frac{{{V_{BAFE}}}}{{{V_{ABCD}}}} = \frac{{BF}}{{BD}} \cdot \frac{{BE}}{{BC}} = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} \Rightarrow {V_{BAFE}} = \frac{1}{4}{V_{ABCD}}.\)
Thể tích khối chóp \[A.EFDC\] là:
\({V_{A \cdot EFDC}} = {V_{ABCD}} - {V_{BAFE}} = {V_{ABCD}} - \frac{1}{4}{V_{ABCD}} = \frac{3}{4}{V_{ABCD}} = {a^3}.\)
Chọn A.Câu 29:
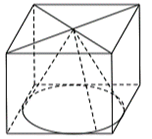
 Xem đáp án
Xem đáp án
Coi khối lập phương có cạnh 1. Thể tích của khối lập phương là \(V = 1.\)
Từ giả thiết, suy ra khối nón có chiều cao \(h = 1\), bán kính đáy \(r = \frac{1}{2}.\)
Thể tích lượng nước trào ra ngoài là thể tích \({V_1}\) của khối nón.
Thể tích lượng nước còn lại trong thùng là \({V_2} = V - {V_1}\).
Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{1}{3}\pi {r^2}h}}{{1 - \frac{1}{3}\pi {r^2}h}} = \frac{{\frac{\pi }{{12}}}}{{1 - \frac{\pi }{{12}}}} = \frac{{12 - \pi }}{{12}}.\) Chọn C.
Câu 30:
Cho số phức \(z\) thỏa mãn \(\left| {z + 1 - 3i} \right| = 2.\) Biết tập hợp điểm biểu diễn số phức \(w = \left( {2 - i} \right)z - 3i + 5\) là một đường tròn. Tâm \(I\) và bán kính của đường tròn đó lần lượt là
 Xem đáp án
Xem đáp án
Ta có: \(w = \left( {2 - i} \right)z - 3i + 5 \Leftrightarrow w = \left( {2 - i} \right)\left( {z + 1 - 3i} \right) + 6 + 4i\)
\( \Leftrightarrow w - 6 - 4i = \left( {2 - i} \right)\left( {z + 1 - 3i} \right)\)\( \Rightarrow \left| {w - 6 - 4i} \right| = \left| {\left( {2 - i} \right)\left( {z + 1 - 3i} \right)} \right| = 2\sqrt 5 \).
Gọi \[M\left( {x\,;\,\,y} \right)\] là điểm biểu diễn số phức \(\left| {w - 6 - 4i} \right| = 2\sqrt 5 \)
\( \Leftrightarrow \left| {\left( {x - 6} \right) + \left( {y - 4} \right)i} \right| = 2\sqrt 5 \)\( \Leftrightarrow {\left( {x - 6} \right)^2} + {\left( {y - 4} \right)^2} = {\left( {2\sqrt 5 } \right)^2}.\)
Vậy tập hợp điểm biểu diễn số \(w\) là đường tròn tâm \(I\left( {6\,;\,\,4} \right)\), bán kính \(R = 2\sqrt 5 .\) Chọn C.
Câu 31:
Cho tích phân \[I = \int\limits_0^4 {\frac{{{\rm{d}}x}}{{3 + \sqrt {2x + 1} }}} = a + b\ln \frac{2}{3}\] với \[a,\,\,b\] là các số nguyên. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đặt \(t = \sqrt {2x + 1} \Leftrightarrow {t^2} = 2x + 1 \Leftrightarrow 2t\;{\rm{d}}t = 2\;{\rm{d}}x \Leftrightarrow {\rm{d}}x = t\;{\rm{d}}t.\) Đổi cận \(\left\{ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow t = 1}\\{x = 4 \Rightarrow t = 3}\end{array}} \right..\)
Do đó \[I = \int\limits_1^3 {\frac{{t\;{\rm{d}}t}}{{3 + t}}} = \int\limits_1^3 {\frac{{t + 3 - 3}}{{t + 3}}} \;{\rm{d}}t = \int\limits_1^3 {\left( {1 - \frac{3}{{t + 3}}} \right)} \;{\rm{d}}t\]
\( = \left. {\left( {t - 3\ln \left| {t + 3} \right|} \right)} \right|_1^3 = \left( {3 - 3\ln 6} \right) - \left( {1 - 3\ln 4} \right) = 2 + 3 \cdot \ln \frac{2}{3}.\)
Vậy \(a = 2,\,\,b = 3\) nên \(a + b = 5.\) Chọn D.
Câu 32:
Tỉnh A đưa ra nghị quyết về việc giảm biên chế công chức, viên chức hưởng lương từ ngân sách Nhà nước trong giai đoạn 5 năm từ 2020 – 2025 là \[12\% \] so với số lượng hiện có năm 2020. Giả sử tỉ lệ giảm hàng năm so với năm trước đó là như nhau. Để đạt được chỉ tiêu đề ra, tỉnh A phải thực hiện tỉ lệ giảm hàng năm tối thiểu là bao nhiêu phần trăm (làm tròn đến 1 chữ số thập phân)?
 Xem đáp án
Xem đáp án
Gọi số công chức, viên chức của tỉnh A năm 2020 là X.
Và \(r\% \) là tỉ lệ giảm hàng năm.
Số công chức, viên chức của tỉnh A năm 2021 là \(X - X \cdot r\% = X \cdot \left( {1 - r\% } \right)\).
Số công chức, viên chức của tỉnh \(A\) năm 2022 là:
\(X \cdot \left( {1 - r\% } \right) - X \cdot \left( {1 - r\% } \right) \cdot r\% = X \cdot {\left( {1 - r\% } \right)^2}\).
Số công chức, viên chức của tỉnh A năm 2023 là \(X \cdot {\left( {1 - r\% } \right)^3}\).
Số công chức, viên chức của tỉnh A năm 2024 là \(X \cdot {\left( {1 - r\% } \right)^4}\).
Số công chức, viên chức của tỉnh A năm 2025 là \(X \cdot {\left( {1 - r\% } \right)^5}\).
Để đạt được chỉ tiêu đề ra thì \(X \cdot {\left( {1 - r\% } \right)^5} = 88\% \cdot \,X \Leftrightarrow {\left( {1 - r\% } \right)^5} = 0,88 \Leftrightarrow r \approx 2,5\% .\) Chọn D.
Câu 33:
Trên mặt phẳng tọa độ \[Oxy,\] cho bốn điểm \[A\left( { - 2\,;\,\,0} \right),\,\,B\left( { - 2\,;\,\,2} \right),\,\,C\left( {4\,;\,\,2} \right),\,\,D\left( {4\,;\,\,0} \right).\] Chọn ngẫu nhiên một điểm có tọa độ \[\left( {x\,;\,\,y} \right)\] (với \[x,\,\,y\] là các số nguyên) nằm trong hình chữ nhật \[ABCD\] (kể cả nằm trên các cạnh). Gọi \[A\] là biến cố "\[x,\,\,y\] đều chia hết cho 2". Xác suất của biến cố \[A\] là
 Xem đáp án
Xem đáp án
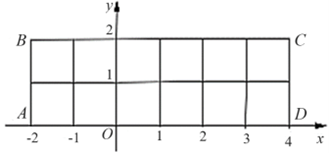
Dựa vào hình vẽ, ta thấy
\( - 2 \le x \le 4\,,\,\,0 \le y \le 2\) và \(x,\,\,y \in \mathbb{Z}.\)
Suy ra \(x \in \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3\,;\,\,4} \right\}\) và \(y \in \left\{ {0\,;\,\,1\,;\,\,2} \right\}.\)
(Mỗi điểm là một giao điểm trên hình vẽ)
Do đó, số phần tử của không gian mẫu là \(n\left( \Omega \right) = 7 \cdot 3 = 21.\)Ta có A: "\[x,\,\,y\] đều chia hết cho 2"
Suy ra \(A = \left\{ {\left( {x\,;\,\,y} \right):x \in \left\{ { - 2\,;\,\,0\,;\,\,2\,;\,\,4} \right\},y \in \left\{ {0\,;\,\,2} \right\}} \right\}.\)
Theo quy tắc nhân, ta có \(n\left( A \right) = 4 \cdot 2 = 8.\)
Vậy xác suất cần tính là \(P = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{8}{{21}}.\) Chọn C.
Câu 34:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) đồng thời thỏa mãn \(f\left( 0 \right) > 0\) và \(\left[ {f\left( x \right) + 6x} \right]f\left( x \right) = 9{x^4} + 3{x^2} + 4\,,\,\,\forall x \in \mathbb{R}.\) Giá trị lớn nhất của hàm số \(y = f\left( {2{x^2} - 3x + 1} \right)\) trên đoạn \[\left[ {0\,;\,\,1} \right]\] bằng
 Xem đáp án
Xem đáp án
Có \(\left[ {f\left( x \right) + 6x} \right]f\left( x \right) = 9{x^4} + 3{x^2} + 4 \Leftrightarrow {\left[ {f\left( x \right) + 3x} \right]^2} = {\left( {3{x^2} + 2} \right)^2}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) + 3x = 3{x^2} + 2}\\{f\left( x \right) + 3x = - 3{x^2} - 2}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = 3{x^2} - 3x + 2}\\{f\left( x \right) = - 3{x^2} - 3x - 2\,\,(L)}\end{array}} \right.} \right.\).
Đặt \(t = 2{x^2} - 3x + 1\), với \(x \in \left[ {0\,;\,\,1} \right]\) thì \(t \in \left[ { - \frac{1}{8};1} \right]\).
Xét hàm \(g(t) = f(t)\) trên \(\left[ { - \frac{1}{8};1} \right]\), có \(g'(t) = f'(t) = 0 \Leftrightarrow 6t - 3 = 0 \Leftrightarrow t = \frac{1}{2} \in \left[ { - \frac{1}{8};1} \right]\).
Có \(g\left( { - \frac{1}{8}} \right) = \frac{{155}}{{64}};\,\,g\left( {\frac{1}{2}} \right) = \frac{5}{4};\,\,g\left( 1 \right) = 2.\)
Suy ra, \({\max _{\left[ {0\,;\,\,1} \right]}}y = {\max _{\left[ { - \frac{1}{8}\,;\,\,1} \right]}}g\left( t \right) = \frac{{155}}{{64}}.\) Chọn C.
Câu 35:
Trong không gian Oxyz, cho đường thẳng \(\Delta :\frac{x}{2} = \frac{{y + 1}}{1} = \frac{{z - 1}}{{ - 1}}\) và hai điểm \(A\left( {1\,;\,\,0\,;\,\,1} \right)\,,\,\,B\left( { - 1\,;\,\,1\,;\,\,2} \right).\) Biết điểm \(M\left( {a\,;\,\,b\,;\,\,c} \right)\) thuộc đường thẳng \(\Delta \) sao cho \(\left| {\overrightarrow {MA} - 3\overrightarrow {MB} } \right|\) đạt giá trị nhỏ nhất. Giá trị của \(a + 2b + 4c\) bằng
 Xem đáp án
Xem đáp án
Do \(M \in \Delta \) nên \(M\left( {2t\,;\,\, - 1 + t\,;\,\,1 - t} \right)\)
\(\overrightarrow {MA} = \left( {1 - 2t\,;\,\,1 - t\,;\,\,t} \right)\);
\(\overrightarrow {MB} = \left( { - 1 - 2t\,;\,\,2 - t\,;\,\,1 + t} \right)\) nên \(3\overrightarrow {MB} = \left( { - 3 - 6t\,;\,\,6 - 3t\,;\,\,3 + 3t} \right)\).
\( \Rightarrow \overrightarrow {MA} - 3\overrightarrow {MB} = \left( {4 + 4t\,;\,\, - 5 + 2t\,;\,\, - 3 - 2t} \right)\);
\(\left| {\overrightarrow {MA} - 3\overrightarrow {MB} } \right| = \sqrt {24{t^2} + 24t + 50} = \sqrt {24{{\left( {t + \frac{1}{2}} \right)}^2} + 44} \ge 44\).
Khi đó \(\left| {\overrightarrow {MA} - 3\overrightarrow {MB} } \right|\) đạt giá trị nhỏ nhất bằng 44 khi \(t = \frac{{ - 1}}{2}\),
Do đó điểm \(M\) có tọa độ là \(M\left( { - 1; - \frac{3}{2};\frac{3}{2}} \right)\) và \(a + 2b + 4c = - 1 - 3 + 6 = 2.\) Chọn D.
Câu 36:
Cho 2 tập khác rỗng \(A = \left( {m - 1\,;\,\,4} \right],\,\,B = \left( { - 2\,;\,\,2m + 2} \right)\) với \(m\) là tham số thực. Có bao nhiêu giá trị nguyên của \(m\) để \(A \subset B\)?
 Xem đáp án
Xem đáp án
Với 2 tập khác rỗng A, B ta có điều kiện \(\left\{ {\begin{array}{*{20}{l}}{m - 1 < 4}\\{2m + 2 > - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 5}\\{m > - 2}\end{array} \Leftrightarrow - 2 < m < 5} \right.} \right..\)
Để \(A \subset B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m - 1 \ge - 2}\\{2m + 2 > 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ge - 1}\\{2m + 2 > 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ge - 1}\\{m > 1}\end{array} \Leftrightarrow m > 1} \right.} \right.} \right..\) So với điều kiện \(1 < m < 5\).
Vậy có 3 giá trị nguyên của \(m\) để \(A \subset B.\)
Đáp án: 3.
Câu 37:
Tìm giới hạn \(B = \mathop {\lim }\limits_{x \to 2} \frac{{{x^4} - 5{x^2} + 4}}{{{x^3} - 8}}.\)
 Xem đáp án
Xem đáp án
Ta có \(B = \mathop {\lim }\limits_{x \to 2} \frac{{{x^4} - 5{x^2} + 4}}{{{x^3} - 8}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 4} \right)}}{{{x^3} - {2^3}}}\)
\[ = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {{x^2} - 1} \right)\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}}\]\( = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {{x^2} - 1} \right)\left( {x + 2} \right)}}{{{x^2} + 2x + 4}} = 1.\)
Đáp án: 1.Câu 38:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thoả mãn \(\int\limits_0^1 {f\left( x \right)} \,dx = 2\) và \(\int\limits_0^2 f \left( {3x + 1} \right){\rm{d}}x = 6.\)
Tính \(I = \int\limits_0^7 {f\left( x \right)} \,{\rm{d}}x.\)
 Xem đáp án
Xem đáp án
Ta có \[\int\limits_0^2 f \left( {3x + 1} \right){\rm{d}}x = 6 \Leftrightarrow \frac{1}{3} \cdot \int\limits_0^2 f \left( {3x + 1} \right){\rm{d}}\left( {3x + 1} \right) = 6 \Leftrightarrow \int\limits_1^7 {f\left( x \right){\rm{d}}x} = 18.\]
Do đó \(I = \int\limits_1^7 {f\left( x \right){\rm{d}}x} = \int\limits_0^1 {f\left( x \right)} \,{\rm{d}}x + \int\limits_1^7 {f\left( x \right)} \,{\rm{d}}x = 2 + 18 = 20.\)
Đáp án: 20.
Câu 39:
Một mảnh vườn hình chữ nhật có diện tích 961m2 người ta muốn mở rộng thêm 4 phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn. Biết tâm hình tròn trùng với tâm của hình chữ nhật. Tính diện tích nhỏ nhất của 4 phần đất được mở rộng (kết quả làm tròn đến chữ số hàng đơn vị).
 Xem đáp án
Xem đáp án
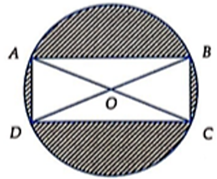
Gọi x, y lần lượt là hai kích thước của mảnh vườn \(\left( {x > 0\,;\,\,y > 0} \right).\)
Và \(R\) là bán kính đường tròn ngoại tiếp mảnh vườn.
Suy ra \({R^2} = O{A^2} = \frac{{A{C^2}}}{4} = \frac{{{x^2} + {y^2}}}{4}\).
Diện tích 4 phần đất mở rộng là \(S = {S_{{\rm{h}}{\rm{.tron }}}} - {S_{ABCD}} = \pi {R^2} - xy\)\( = \pi \cdot \frac{{{x^2} + {y^2}}}{4} - xy \ge \pi \cdot \frac{{2xy}}{4} - xy = \left( {\frac{\pi }{2} - 1} \right)xy = \left( {\frac{\pi }{2} - 1} \right) \cdot 961 \approx 549\,\,\left( {{m^2}} \right){\rm{. }}\)
Đáp án: 549.
Câu 40:
Lớp 12A có 22 học sinh gồm 15 nam và 7 nữ. Cần chọn và phân công 4 học sinh lao động trong đó có 1 bạn lau bảng, 1 bạn lau bàn và 2 bạn quét nhà. Có bao nhiêu cách chọn và phân công sao cho trong 4 học sinh đó có ít nhất một bạn nữ?
 Xem đáp án
Xem đáp án
Số cách chọn và phân công 4 học sinh bất kì là:
\(C_{22}^1 \cdot C_{21}^1 \cdot C_{20}^2 = 87\,\,780\) (cách).
Số cách chọn và phân công 4 học sinh mà chỉ có học sinh nam là:
\(C_{15}^1 \cdot C_{14}^1 \cdot C_{13}^2 = 16\,\,380\) (cách).
Do đó, số cách chọn và phân công 4 học sinh đó có ít nhất một học sinh nữ là:
\(87\,\,780 - 16\,\,380 = 71\,\,400\) (cách).
Đáp án: \[{\bf{71}}\,\,{\bf{400}}\].
Câu 41:
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thoả mãn \(f\left( x \right) > - 1\,,\,\,f\left( 0 \right) = 0\) và \(f'\left( x \right)\sqrt {{x^2} + 1} = 2x\sqrt {f\left( x \right) + 1} .\) Tính \(f\left( {\sqrt 3 } \right).\)
 Xem đáp án
Xem đáp án
Ta có: \(f'\left( x \right)\sqrt {{x^2} + 1} = 2x\sqrt {f\left( x \right) + 1} \Leftrightarrow \frac{{f'\left( x \right)}}{{\sqrt {f\left( x \right) + 1} }} = \frac{{2x}}{{\sqrt {{x^2} + 1} }}\)
\[ \Leftrightarrow \int\limits_0^{\sqrt 3 } {\frac{{f'\left( x \right)}}{{\sqrt {f\left( x \right) + 1} }}} \,dx = \int\limits_0^{\sqrt 3 } {\frac{{2x}}{{\sqrt {{x^2} + 1} }}} \left. {dx \Leftrightarrow \sqrt {f\left( x \right) + 1} } \right|_0^{\sqrt 3 } = \left. {\left. {\sqrt {{x^2} + 1} } \right|_0^{\sqrt 3 } \Leftrightarrow \sqrt {f\left( x \right) + 1} } \right|_0^{\sqrt 3 } = 1\]
\( \Leftrightarrow \sqrt {f\left( {\sqrt 3 } \right) + 1} - \sqrt {f\left( 0 \right) + 1} = 1 \Leftrightarrow \sqrt {f\left( {\sqrt 3 } \right) + 1} = 2 \Leftrightarrow f\left( {\sqrt 3 } \right) = 3.\)
Đáp án: 3.
Câu 42:
Trong không gian \[Oxyz,\] cho mặt cầu \((S):{x^2} + {y^2} + {z^2} + 4x - 6y + m = 0\) (\(m\) là tham số) và đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 4 + 2t}\\{y = 3 + t}\\{z = 3 + 2t}\end{array}} \right..\) Biết đường thẳng \(\Delta \) cắt mặt cầu \((S)\) tại hai điểm phân biệt \[A,\,\,B\] sao cho \(AB = 8.\) Giá trị của \(m\) là
 Xem đáp án
Xem đáp án
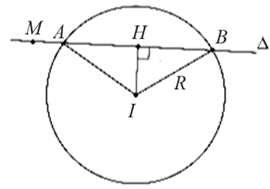
Gọi \(H\) là trung điểm đoạn thẳng \(AB \Rightarrow IH \bot AB\,,\,\,HA = 4.\)
Mặt cầu \((S)\) có tâm \(I\left( { - 2\,;\,\,3\,;\,\,0} \right)\), bán kính \(R = \sqrt {13 - m} ,\,\,\left( {m < 13} \right).\)
Đường thẳng đi qua \(M\left( {4\,;\,\,3\,;\,\,3} \right)\) và có một vectơ chỉ phương \(\vec u = \left( {2\,;\,\,1\,;\,\,2} \right).\)Ta có: \(\overrightarrow {IM} = \left( {6\,;\,\,0\,;\,\,3} \right) \Rightarrow \left[ {\overrightarrow {IM} \,,\,\,\vec u} \right] = \left( { - 3\,;\,\, - 6\,;\,\,6} \right)\)\( \Rightarrow IH = d\left( {I,\,\,\Delta } \right) = \frac{{\left| {\left[ {\overrightarrow {IM} \,,\,\,\vec u} \right]} \right|}}{{\left| {\vec u} \right|}} = 3.\)
Ta có: \({R^2} = I{H^2} + H{A^2} \Leftrightarrow 13 - m = {3^2} + {4^2} \Leftrightarrow m = - 12.\)
Đáp án: −12.
Câu 43:
Tìm giá trị của tham số \(m\) để phương trình \({4^x} - 2m \cdot {2^x} + 2m = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \({x_1} + {x_2} = 3\)?
 Xem đáp án
Xem đáp án
Đặt \(t = {2^x} > 0\) nên phương trình đã cho trở thành: \({t^2} - 2mt + 2m = 0\,\,\,(*).\)
Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow (*)\) có hai nghiệm dương phân biệt \({t_1},{t_2}.\)
Ta có \({t_1}{t_2} = {2^{{x_1}}} \cdot {2^{{x_2}}} = {2^{{x_1} + {x_2}}} = {2^3} = 8 = 2m\) suy ra \(m = 4\) (thỏa mãn điều kiện).
Vậy \(m = 4\) là giá trị duy nhất cần tìm.
Đáp án: 1.
Câu 44:
Cho hàm số \(y = \left| {{x^4} - 4{x^3} + 4{x^2} + m} \right|\) với \(m\) là tham số. Tổng tất cả các giá trị của tham số \(m\) để \(2{\min _{\left[ {1\,;\,\,3} \right]}}y + {\max _{\left[ {1\,;\,\,3} \right]}}y = 12\) bằng
 Xem đáp án
Xem đáp án
Xét hàm số \(f(x) = {x^4} - 4{x^3} + 4{x^2} + m\) trên \(\left[ {1\,;\,\,3} \right] \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{\min }_{\left[ {1\,;\,\,3} \right]}}f(x) = m}\\{{{\max }_{\left[ {1\,;\,\,3} \right]}}f(x) = m + 9}\end{array}} \right..\)
• TH1: Với \(m > 0\) suy ra \(\left\{ {\begin{array}{*{20}{l}}{{y_{\min }} = m}\\{{y_{\max }} = m + 9}\end{array}} \right.\).
Do đó \(2{y_{\min }} + {y_{\max }} = 2m + m + 9 = 12 \Leftrightarrow m = 1\) (thoả mãn).
• TH2: Với \(m + 9 < 0 \Leftrightarrow m < - 9\) suy ra \(\left\{ {\begin{array}{*{20}{l}}{{y_{\min }} = \left| {m + 9} \right|}\\{{y_{\max }} = \left| m \right|}\end{array}} \right.\).
Do đó \(2{y_{\min }} + {y_{\max }} = 2\left| {m + 9} \right| + \left| m \right| = 12 \Leftrightarrow 2\left( { - m - 9} \right) - m = 12 \Leftrightarrow m = - 10\) (thoả mãn).
• TH3: Với \( - 9 < m < 0\) suy ra \[\left\{ {\begin{array}{*{20}{l}}{{y_{\min }} = 0}\\{{y_{\max }} = \left\{ {\left| m \right|;\,\,\left| {m + 9} \right|} \right\}}\end{array}} \right.\].
Do đó \(2{y_{\min }} + {y_{\max }} = 12 \Leftrightarrow {y_{\max }} = 12 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left| m \right| = 12}\\{\left| {m + 9} \right| = 12}\end{array}} \right.\) (không thoả mãn).
Nên \(m \in \left\{ { - 10\,;\,\,1} \right\}\). Do đó, tổng các giá trị của \[m\] là \( - 10 + 1 = - 9\).
Đáp án: −9.
Câu 45:
Trong không gian \[Oxyz,\] tính khoảng cách từ giao điểm của hai đường thẳng \({d_1},\,\,{d_2}\) đến mặt phẳng \((P)\), biết rằng \(\left( {{d_1}} \right):\frac{{x + 1}}{2} = \frac{y}{3} = \frac{{z - 1}}{3},\,\,\left( {{d_2}} \right):\frac{{ - x + 1}}{2} = \frac{y}{1} = \frac{{z - 1}}{1}\) và \((P):2x + 4y - 4z - 3 = 0?\)
 Xem đáp án
Xem đáp án
Phương trình tham số của hai đường thẳng \({d_1},\,\,{d_2}\) như sau:
\({d_1}:\left\{ {\begin{array}{*{20}{l}}{x = - 1 + 2t}\\{y = 3t}\\{z = 1 + 3t}\end{array},\,\,{d_2}:\left\{ {\begin{array}{*{20}{l}}{x = 1 - 2t'}\\{y = t'}\\{z = 1 + t'}\end{array}} \right.} \right.\).
Xét hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{ - 1 + 2t = 1 - 2t'}\\{3t = t'}\\{t + 3t = 1 + t'}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{2t + 2t' = 2}\\{3t - t' = 0}\\{3t - t' = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t = \frac{1}{4}}\\{t' = \frac{3}{4}}\end{array}} \right.} \right.} \right.\).
Suy ra giao điểm của \({d_1},\,\,{d_2}\) là \(A\left( { - \frac{1}{2}\,;\,\,\frac{3}{4}\,;\,\,\frac{7}{4}} \right).\)
Khoảng cách từ \(A\) đến mặt phẳng \((P)\) là \(d\left( {A\,,\,\,\left( P \right)} \right) = \frac{{\left| {2 \cdot \left( { - \frac{1}{2}} \right) + 4 \cdot \left( {\frac{3}{4}} \right) - 4 \cdot \left( {\frac{7}{4}} \right) - 3} \right|}}{{\sqrt {{2^2} + {4^2} + {{\left( { - 4} \right)}^2}} }} = \frac{4}{3}.\)
Đáp án: \(\frac{4}{3}.\)
Câu 46:
Cho các số phức \({z_1} = - 2 + i,{z_2} = 2 + i\) và số phức \(z\) thay đổi thỏa mãn \({\left| {z - {z_1}} \right|^2} + {\left| {z - {z_2}} \right|^2} = 16.\) Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \[\left| z \right|\]. Giá trị biểu thức \({M^2} - {m^2}\) bằng
 Xem đáp án
Xem đáp án
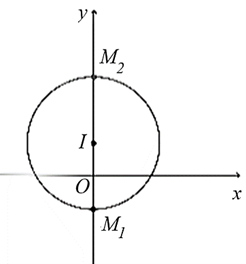
Gọi \(M\) là điểm biểu diễn của \[z.\]
Gọi \(A\left( { - 2\,;\,\,1} \right),\,\,B\left( {2\,;\,\,1} \right).\) Gọi \(I\left( {0\,;\,\,1} \right)\) là trung điểm AB.
Ta có \({\left| {z - {z_1}} \right|^2} + {\left| {z - {z_2}} \right|^2} = 16 \Leftrightarrow M{A^2} + M{B^2} = 16\)
\(M{A^2} + M{B^2} = 2M{I^2} + \frac{{A{B^2}}}{2} = 16 \Rightarrow MI = 2\).
Suy ra tập hợp các điểm \(M\) là đường tròn tâm \(I\left( {0\,;\,\,1} \right)\) bán kính \(R = 2.\)
Ta lại có: \(\left| {IM - IO} \right| \le IM \le IM + IO \Leftrightarrow 1 \le OM \le 3.\)Do đó \({\left| z \right|_{\max }} = 3 \Leftrightarrow M = {M_2}\); \({\left| z \right|_{{\rm{min }}}} = 1 \Leftrightarrow M = {M_1}\)\( \Rightarrow {M^2} - {m^2} = 8.\)
Đáp án: 8.
Câu 47:
 Xem đáp án
Xem đáp án
Đặt \(u(x) = {x^2} - 4x \Rightarrow u' = 2x - 4 = 0 \Rightarrow x = 2\).
Đặt \(t = u\left( {\left| x \right|} \right) = {\left| x \right|^2} - 4\left| x \right|\).
Vẽ đồ thị hàm số \(u(x) = {x^2} - 4x\), từ đó suy ra đồ thị \(t = u\left( {\left| x \right|} \right)\).
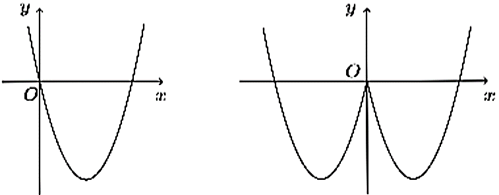
Ta có bảng biến thiên:
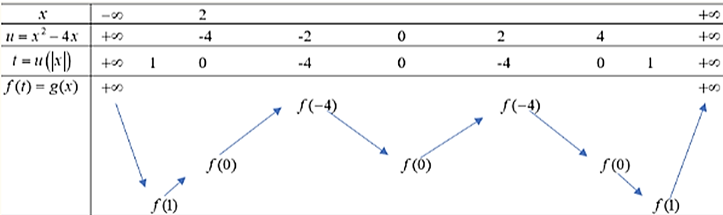
Suy ra hàm số \(y = g(x) = f\left( {{x^2} - 4\left| x \right|} \right)\) có tất cả 5 điểm cực trị.
Đáp án: 5.
Câu 48:
Cho hai số x, y thỏa mãn \(2x + y > 0\) và \(\frac{{2{e^x}}}{{\sqrt {2x + y} }} + \ln (2x + y) = 2x + 2.\) Giá trị nhỏ nhất của \[y\] là
 Xem đáp án
Xem đáp án
Đặt \(t = \ln \sqrt {2x + y} \Leftrightarrow \sqrt {2x + y} = {e^t} \Leftrightarrow 2x + y = {e^{2t}}\).
Khi đó, giả thiết trở thành: \(\frac{{2{e^x}}}{{{e^t}}} + \ln {e^{2t}} = 2x + 2 \Leftrightarrow 2{e^{x - t}} + 2t - 2x - 2 = 0\)
\( \Leftrightarrow {e^{x - t}} - \left( {x - t} \right) - 1 = 0 \Leftrightarrow f\left( A \right) = {e^A} - A - 1 = 0\)
Khảo sát hàm số \(f\left( A \right) \Rightarrow f\left( A \right) \Leftrightarrow A = 0.\)
Do đó \(x - t = 1 \Leftrightarrow x - \ln \sqrt {2x + y} = 1 \Leftrightarrow \ln \sqrt {2x + y} = x - 1\)
\( \Leftrightarrow \sqrt {2x + y} = {e^{x - 1}} \Leftrightarrow 2x + y = {e^{2x - 2}} \Leftrightarrow y = {e^{2x - 2}} - 2x{\rm{. }}\)
Khảo sát hàm số \(g\left( x \right) = {e^{2x - 2}} - 2x\) suy ra \[\min y = \min g\left( x \right) = - 1.\] Đáp án: −1.
Câu 49:
Cho hình chóp \[S.ABCD\] có đáy là hình vuông, mặt bên \(\left( {SAB} \right)\) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy \(\left( {ABCD} \right)\) và có diện tích bằng \(\frac{{27\sqrt 3 }}{4}.\) Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy \(\left( {ABCD} \right)\) chia khối chóp \[S.ABCD\] thành hai phần. Thể tích \(V\) của phần chứa điểm \(S\) bằng
 Xem đáp án
Xem đáp án
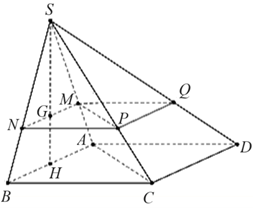
Gọi \(H\) là trung điểm \(AB\). Do \(\Delta SAB\) đều và \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right).\)
Ta có \({S_{SAB}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{27\sqrt 3 }}{4} \Rightarrow AB = 3\sqrt 3 \)
\( \Rightarrow SH = \frac{{AB\sqrt 3 }}{2} = \frac{{3\sqrt 3 \sqrt 3 }}{2} = \frac{9}{2}\)\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SH = \frac{1}{3} \cdot A{B^2} \cdot SH = \frac{1}{3} \cdot {\left( {3\sqrt 3 } \right)^2} \cdot \frac{{{9^2}}}{2} = \frac{{81}}{2}\) (đvtt).
Gọi \(G\) là trọng tâm tam giác \[SAB,\] qua \(G\) kẻ đường thẳng song song với \[AB,\] cắt \[SA\] và \[SB\] lần lượt tại \[M,{\rm{ }}N.\]
Qua \(N\) kẻ đường thẳng song song với \[BC\] cắt \[SC\] tại \(P\), qua \(M\) kẻ đường thẳng song song với \[AD\] cắt \[SD\] tại \[Q.\]
Suy ra \(\left( {MNPQ} \right)\) là mặt phẳng đi qua \(G\) và song song với \(\left( {ABCD} \right)\).
Khi đó \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} = \frac{{SP}}{{SC}} = \frac{{SQ}}{{SD}} = \frac{{SG}}{{SH}} = \frac{2}{3}.\)
Ta có \(\frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}} \cdot \frac{{SN}}{{SB}} \cdot \frac{{SP}}{{SC}} = {\left( {\frac{2}{3}} \right)^2} = \frac{8}{{27}}\)\( \Rightarrow {V_{S.MNP}} = \frac{8}{{27}} \cdot {V_{S.ABC}} = \frac{8}{{27}} \cdot \frac{1}{2}{V_{S.ABCD}} = \frac{4}{{27}}{V_{S.ABCD}}\)
\(\frac{{{V_{S.MPQ}}}}{{{V_{S.ACD}}}} = \frac{{SM}}{{SA}} \cdot \frac{{SP}}{{SC}} \cdot \frac{{SQ}}{{SD}} = {\left( {\frac{2}{3}} \right)^2} = \frac{8}{{27}} \Rightarrow {V_{S.MPQ}} = \frac{8}{{27}} \cdot {V_{S.ACD}} = \frac{8}{{27}} \cdot \frac{1}{2}{V_{S.ABCD}} = \frac{4}{{27}}{V_{S.ABCD}}\)
Vậy \({V_{S.MNPQ}} = {V_{S.MNP}} + {V_{S.MPQ}} = \frac{4}{{27}}{V_{S.ABCD}} + \frac{4}{{27}}{V_{S.ABCD}} = \frac{8}{{27}}{V_{S.ABCD}} = \frac{8}{{27}} \cdot \frac{{81}}{2} = 12\) (đvtt).
Đáp án: 12.
Câu 50:
Cho nửa đường tròn đường kính \(AB = 2R\) và điểm \(C\) thay đổi trên nửa đường tròn đó, đặt \(\widehat {CAB} = \alpha ^\circ \) và gọi \(H\) là hình chiếu vuông góc của \(C\) lên \[AB.\] Tìm \(\alpha \) sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác \[ACH\] quanh trục \[AB\] đạt giá trị lớn nhất (kết quả làm tròn đến hàng đơn vị).
 Xem đáp án
Xem đáp án
Khi quay tam giác \[ACH\] quanh trục \[AB,\] ta được khối nón đỉnh \(A\), có đáy là hình tròn tâm \(H\), bán kính \[HC.\]
Đặt \(AH = h\,;\,\,CH = r.\) Ta có \(V = \frac{1}{3}\pi {r^2}h.\)
Áp dụng hệ thức lượng trong tam giác \[ACB,\] ta có \(C{H^2} = HA \cdot HB\).
Mà \(HB = 2R - h\) suy ra \[{r^2} = h\left( {2R - h} \right) \Rightarrow V = \frac{1}{3}\pi h\left( {2R - h} \right)h\]
Để thể tích khối tròn xoay lớn nhất thì \[\left( {2R - h} \right){h^2}\] lớn nhất.
Xét hàm số \(f\left( h \right) = 2R.{h^2} - {h^3}\) trên \(\left( {0\,;\,\,2R} \right)\), có \(f'\left( h \right) = 4R.h - 3{h^2} = 0 \Rightarrow h = \frac{{4R}}{3}.\)
Suy ra \(\max f\left( h \right) = f\left( {\frac{{4R}}{3}} \right) \Rightarrow r = \sqrt {\frac{{4R}}{3} \cdot \left( {2R - \frac{{4R}}{3}} \right)} = \frac{{2\sqrt 2 R}}{3}\).
Vậy \(\tan \alpha = \frac{{CH}}{{AH}} = \frac{r}{h} = \frac{{\sqrt 2 }}{2} \Rightarrow \alpha = \arctan \frac{{\sqrt 2 }}{2} \approx 35^\circ .\)
Đáp án: 35.
Câu 51:
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
 Xem đáp án
Xem đáp án
Để trả lời được câu hỏi, cần hiểu nôm na “giọng điệu”: giọng nói, lối nói biểu hiện một thái độ nhất định và có thể xác định thông qua: từ ngữ thơ và cách ngắt nhịp thơ. Ở ngữ cảnh trên, phương án B có thể loại ngay vì tác giả đang nói về những đứa con tinh thần quý báu của mình nên không thể là mỉa mai, giễu cợt. Phương án A, D mô tả không chính xác sắc thái và giọng điệu của đoạn thơ vì không có từ nào thể hiện sự ngông nghênh hay ngang tàng. Chọn C.
Câu 52:
 Xem đáp án
Xem đáp án
Đặt từ “man” vào ngữ cảnh (câu thơ: Bẩm con không dám man cửa Trời) ta sẽ suy ra ý nghĩa của cả câu thơ: Bẩm con không dám nói sai/nói dối ở cửa Trời, vậy nên phương án đúng là A (nói dối). Chọn A.
Câu 53:
 Xem đáp án
Xem đáp án
Các khái niệm về văn chương mà Tản Đà nhắc đến trong đoạn thơ đều do ông tự gọi tên. Ta có thể căn cứ vào nghĩa của từ “chơi” (vui chơi, giải trí) và các tác phẩm được liệt kê trong khái niệm văn chơi (Khối tình con) để suy luận ra đây là khái niệm chỉ những tác phẩm văn chương có tính giải trí, tạo ra sự khác biệt với “văn thuyết lí” (văn dùng để giảng giải về đạo đức) ở câu trên. Chọn C.
Câu 54:
 Xem đáp án
Xem đáp án
Đọc đoạn thơ, ta thấy tác giả chủ yếu sử dụng biện pháp liệt kê để “khoe” các sáng tác của mình ở nhiều lĩnh vực khác nhau (tên các tác phẩm và thể loại) nhằm khẳng định tài năng đa dạng, phong phú của bản thân. Chọn C.
Câu 55:
 Xem đáp án
Xem đáp án
Đoạn thơ không nhắc đến các trải nghiệm sống của Tản Đà mà chỉ nhắc tới các tác phẩm văn chương của ông → Loại phương án D. Trong đoạn trích có chứa các từ khóa “văn thuyết lí”, “văn chơi”, “tiểu thuyết”, “văn vị đời”, “văn dịch”... điều này chỉ khẳng định sự đa dạng về thể loại và phong cách mà không nhắc tới giọng văn riêng biệt của Tản Đà → Loại phương án B. Đoạn thơ là Tản Đà tự kể tên các tác phẩm của mình, không có sự so sánh hay khẳng định sự độc đáo của riêng mình → Loại phương án A. Chọn C.
Câu 56:
 Xem đáp án
Xem đáp án
Đoạn trích có các dữ kiện: “Thiên nhiên đóng vai trò hết sức quan trọng đối việc học tập ở trẻ em” và “Khi tương tác với các sự vật trong tự nhiên, từ cây cối đến động vật, trẻ em được tiếp xúc với nguồn cảm hứng vô tận, từ đó phát triển về tình cảm, kĩ năng xã hội và có thêm động lực học tập”. → Vai trò của thiên nhiên đối với việc học tập và phát triển của trẻ em. Chọn A.
Câu 57:
 Xem đáp án
Xem đáp án
Đoạn trích có nhắc tới các dữ kiện:
- Hoạt động ngoài trời giúp trẻ em tự tin hơn, năng động, hoạt bát hơn, cải thiện sự quan tâm, mối quan hệ và sự tương tác với người lớn.
- Được chìm đắm trong vẻ đẹp sống động của những cánh rừng, những bờ biển và đồng cỏ... giúp trẻ phát triển những kĩ năng cơ bản như nhận biết, xác định, phân tích và đánh giá.
- Khi tương tác với các sự vật trong tự nhiên, từ cây cối đến động vật, trẻ em được tiếp xúc với nguồn cảm hứng vô tận, từ đó phát triển về tình cảm, kĩ năng xã hội và có thêm động lực học tập.
- Không có dữ kiện nào nhắc tới: Hoạt động ngoài trời giúp trẻ em phát triển về thể chất và các kĩ năng vận động. Chọn D.
Câu 58:
 Xem đáp án
Xem đáp án
Trong đoạn trích có câu: “Bên cạnh đó, trẻ còn được phát triển kĩ năng định lượng với hoạt động đếm côn trùng và hoa”. Chọn A.
Câu 59:
 Xem đáp án
Xem đáp án
Câu cuối cùng của đoạn trích: “Quá trình thích ứng với thế giới tự nhiên thay đổi không ngừng và thường không thể dự báo sẽ giúp trẻ em học cách thích nghi và giải quyết vấn đề”. Chọn C.
Câu 60:
 Xem đáp án
Xem đáp án
Trong đoạn trích có câu: “Khi tương tác với các sự vật trong tự nhiên, từ cây cối đến động vật, trẻ em được tiếp xúc với nguồn cảm hứng vô tận, từ đó phát triển về tình cảm, kĩ năng xã hội và có thêm động lực học tập”. Chọn A.
Câu 61:
 Xem đáp án
Xem đáp án
Phương thức biểu đạt chính của đoạn thơ là biểu cảm. Chọn A.
Câu 62:
 Xem đáp án
Xem đáp án
Đoạn thơ được viết theo thể thơ tự do. Số dòng, số tiếng không hạn định; gieo vần, ngắt nhịp linh hoạt,… Chọn A.
Câu 63:
Biện pháp tu từ nào được sử dụng trong đoạn thơ:
Tôi ăn biển hàng ngày từng hạt muối trắng tinh
Tôi ăn bình minh mọc lên nắng mặn
Tôi ăn gió thổi về từ biển
Tôi ăn rì rầm sóng.
 Xem đáp án
Xem đáp án
Phép điệp: “Tôi ăn…”. Chọn C.
Câu 64:
 Xem đáp án
Xem đáp án
Câu thơ “Nước mắt vợ thành sông chảy ra biển tìm chồng” khơi gợi nỗi đau mất người chồng của người vợ làng chài. Chọn D.
Câu 65:
Nội dung chính của đoạn thơ dưới đây là gì?
Những đứa con như cây lim cây sến
Từ rừng đổ xuống
Từ châu thổ trồi lên
Những đứa con xẻ gỗ đóng thuyền
Rút dây rừng đan lưới.
 Xem đáp án
Xem đáp án
Đoạn thơ nói về hành trình ra khơi tiếp nối cha ông của thế hệ sau. Chọn C.
Câu 66:
 Xem đáp án
Xem đáp án
Đoạn trích sử dụng phong cách ngôn ngữ nghệ thuật. Chọn A.
Câu 67:
 Xem đáp án
Xem đáp án
Sống trong không khí ngày xuân, đặc biệt là khi nghe thấy tiếng sáo gọi bạn tình, Mị thổn thức nhớ về quá khứ và để quên đi thực tại đau khổ, Mị đã tìm đến với rượu. Cách uống “ực từng bát” của Mị phần nào đã thể hiện điều đó. Chọn C.
Câu 68:
 Xem đáp án
Xem đáp án
Câu 69:
 Xem đáp án
Xem đáp án
Khi nghe tiếng sáo gọi bạn tình, trong một khoảnh khắc nhất định, Mị bỗng nhớ về quá khứ tươi đẹp và cô được sống với cảm giác vui sướng, hạnh phúc trong chốc lát. Chọn C.
Câu 70:
 Xem đáp án
Xem đáp án
Nghệ thuật nổi bật của đoạn trích là miêu tả tâm lí nhân vật tinh tế, sâu sắc. Chọn A.
Câu 71:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Phát biểu cảm nghĩ về một tác phẩm văn học (bài văn, bài thơ) là trình bày những cảm xúc, tưởng tượng, liên tưởng, suy ngẫm của mình về nội dung và giá trị của tác phẩm đó.
 Xem đáp án
Xem đáp án
Phát biểu cảm nghĩ về một tác phẩm văn học (bài văn, bài thơ) là trình bày những cảm xúc, tưởng tượng, liên tưởng, suy ngẫm của mình về nội dung và hình thức của tác phẩm đó. Chọn D.
Câu 72:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Truyện ngắn “Vợ nhặt” của Kim Lân không chỉ miêu tả tình cảnh thê thảm của người nông dân trong nạn đói năm 1945 mà còn khẳng định bản chất tốt đẹp và những hi vọng về một tương lai sáng lạng của họ.
 Xem đáp án
Xem đáp án
Từ “sáng lạng” sai chính tả vì gần âm với từ “xán lạn”. Chọn D.
Câu 73:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Nam Cao từng làm nhiều nghề, vạ vật kiếm sống và đến với văn chương đầu tiên vì mục đích mưu sinh. Năm 18 tuổi vào Sài Gòn, ông nhận làm thư kí cho một hiệu may, bắt đầu viết các truyện ngắn “Cảnh cuối cùng”, “Hai cái xác”.
 Xem đáp án
Xem đáp án
Đọc đoạn văn, xác định từ “vạ vật” (tính từ thể hiện việc tùy ý ngồi ở một nơi nào đó do không được quan tâm tới) đang dùng sai nghĩa, cần thay bằng từ “chật vật” (cuộc sống vất vả, khó khăn). Chọn A.
Câu 74:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Qua mỗi lần như vậy, người ta sẽ tích lũy được nhiều kinh nghiệm và thành công nhất định về sau.
 Xem đáp án
Xem đáp án
Lỗi diễn đạt (logic) sắp xếp trật tự các thành phần trong câu một cách lộn xộn làm câu văn khó hiểu. Sửa: Qua mỗi lần như vậy, người ta sẽ tích lũy được nhiều kinh nghiệm và về sau nhất định thành công. Chọn D.
Câu 75:
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Xưa nay, không ai chết đến lần thứ hai mà được bài học kinh nghiệm về cách chết.
 Xem đáp án
Xem đáp án
Từ “mà” dùng sai. Nên thay bằng từ “để”. Xưa nay, không ai chết đến lần thứ hai để được bài học kinh nghiệm về cách chết. Chọn C.
Câu 76:
 Xem đáp án
Xem đáp án
Các từ “ưu điểm, thế mạnh, điểm tốt” đều chỉ mặt mạnh, những điều tốt đã thực hiện được còn “trọng điểm” là những vấn đề, những nơi có vai trò quan trọng. Chọn A.
Câu 77:
 Xem đáp án
Xem đáp án
Các tác phẩm: “Chiếc thuyền ngoài xa, Vợ nhặt, Vợ chồng A Phủ” thuộc thể loại truyện ngắn còn “Tuyên ngôn Độc lập” thuộc thể văn chính luận. Chọn C.
Câu 78:
 Xem đáp án
Xem đáp án
“Số đỏ” là tác phẩm thuộc thể loại tiểu thuyết, các tác phẩm còn lại đều là tác phẩm truyện ngắn. Chọn D.
Câu 79:
 Xem đáp án
Xem đáp án
Nguyễn Tuân thuộc dòng văn xuôi lãng mạn. Còn lại các tác giả đều thuộc dòng văn hiện thực. Chọn D.
Câu 80:
 Xem đáp án
Xem đáp án
Tác phẩm “Hồn Trương Ba, da hàng thịt” thuộc thể loại kịch. Các tác phẩm còn lại thuộc thể truyện ngắn. Chọn B.
Câu 81:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Theo Trung tâm Dự báo khí tượng thủy văn quốc gia, từ đêm 26 đến ngày 28/12, trên nhiều vùng biển có gió đông bắc mạnh đến cấp 7, giật cấp 8-9, sóng biển cao từ 4-6m. Cảnh báo, toàn bộ tàu thuyền và các hoạt động trên nhiều vùng biển đều có nguy cơ cao ________ tác động của gió mạnh, sóng lớn và mưa dông.
 Xem đáp án
Xem đáp án
Việc xảy ra thiên tai như sóng to, gió lớn thường mang đến những điều không hay, bất lợi con người, động từ “chịu” có nghĩa là nhận lấy điều không hay, bất lợi cho mình; thích ứng hoặc tiếp nhận một tác động nào đó, thường là không hay, từ bên ngoài. Còn các động từ như “được, hưởng, nhận” thường mang tính tích cực, không phù hợp với ngữ cảnh này. Từ cần điền vào chỗ trống là “chịu”. Chọn C.
Câu 82:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Văn hóa Việt Nam đã _________ nên tâm hồn, khí phách, bản lĩnh con người Việt Nam, anh hùng, mến khách, yêu quý bạn bè, làm rạng rỡ lịch sử vẻ vang của dân tộc.
 Xem đáp án
Xem đáp án
Câu 83:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Phải chăng cái chết không phải là điều mất mát lớn nhất trong cuộc đời. Sự _______ lớn nhất là bạn để cho tâm hồn tàn lụi ngay khi còn sống.
 Xem đáp án
Xem đáp án
Phải chăng cái chết không phải là điều mất mát lớn nhất trong cuộc đời. Sự mất mát lớn nhất là bạn để cho tâm hồn tàn lụi ngay khi còn sống. Từ “mất mát” điền vào chỗ trống sẽ có tác dụng liên kết giữa câu trước và câu sau. Chọn D.
Câu 84:
Chọn từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Truyện ngắn “Chí Phèo” của Nam Cao đã khái quát một hiện tượng xã hội ở nông thôn Việt Nam trước Cách mạng: một bộ phận nông dân lao động lương thiện bị đẩy vào con đường _________, _________
 Xem đáp án
Xem đáp án
Chí Phèo từ một người nông dân hiền lành lương thiện bị đánh mất dần phẩm chất đạo đức, trở nên xấu xa, tồi tệ nên sử dụng từ “tha hóa” và “lưu manh hóa” là thích hợp nhất. Còn “bần cùng hóa, nghèo đói, cùng cực” là cuộc sống chung của người dân lúc bấy giờ chưa mang tính điển hình. Chọn A.
Câu 85:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Tất cả khung cảnh ấy nhìn qua những cái mắt lưới và tấm lưới nằm giữa hai chiếc gọng vó hiện ra dưới một hình thù y hệt cảnh một con dơi, toàn bộ khung cảnh từ đường nét đến ánh sáng đều hài hòa và đẹp, một vẻ đẹp thực đơn giản và toàn bích khiến đứng trước nó tôi trở nên bối rối, trong trái tim như có cái gì _________ vào.
 Xem đáp án
Xem đáp án
Đây là câu văn trích từ tác phẩm “Chiếc thuyền ngoài xa” của nhà văn Nguyễn Minh Châu mà học sinh đã được học. Từ thích hợp điền vào chỗ trống là “bóp thắt” thể hiện một cảm xúc ngỡ ngàng, ngạc nhiên, xúc động mạnh của người nghệ sĩ Phùng khi chiêm ngưỡng vẻ đẹp toàn bích, toàn thiện của thiên nhiên, tạo vật. Chọn C.
Câu 86:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Cô bảo tôi: “Mày bắt nạt vợ mày quá, không để nó tự quyết định bất cứ việc gì, vậy là hỏng. Người đàn bà không là nội tướng thì cái gia đình ấy cũng chẳng ra sao”. Khi các con còn nhỏ, ngồi vào bàn ăn cô thường chú ý sửa chữa cách ngồi, cách cầm bát cầm đũa, cách múc canh, cả cách nói chuyện trong bữa ăn. Cô vẫn răn lũ con tôi: “Chúng mày là người Hà Nội thì cách đi đứng nói năng phải có chuẩn, không được sống tùy tiện, buông tuồng”. Có lần tôi cãi: “Chúng tôi là người của thời loạn, các cụ lại bắt dạy con cái theo thời bình là khó lắm”. Cô ngồi ngẩn ra một lúc, rồi bảo: “Tao chỉ dạy chúng nó biết tự trọng, biết xấu hổ còn sau này muốn sống ra sao là tùy”.
(Một người Hà Nội – Nguyễn Khải)
 Xem đáp án
Xem đáp án
Chi tiết: Khi các con còn nhỏ, ngồi vào bàn ăn cô thường chú ý sửa chữa cách ngồi, cách cầm bát cầm đũa, cách múc canh, cả cách nói chuyện trong bữa ăn. Cô vẫn răn lũ con tôi: “Chúng mày là người Hà Nội thì cách đi đứng nói năng phải có chuẩn, không được sống tùy tiện, buông tuồng” cho thấy cô Hiền là người trân trọng, giữ gìn những truyền thống văn hóa tốt đẹp của người Hà Nội. Chọn B.
Câu 87:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thôn Đoài ngồi nhớ thôn Đông
Một người chín nhớ mười mong một người.
Gió mưa là bệnh của giời
Tương tư là bệnh của tôi yêu nàng.
Hai thôn chung lại một làng,
Cớ sao bên ấy chẳng sang bên này?.
(Tương tư – Nguyễn Bính)
 Xem đáp án
Xem đáp án
Câu thơ sử dụng biện pháp tu từ hoán dụ: dùng địa danh để chỉ người sống trên địa danh đó: Thôn Đoài - Thôn Đông → Cách biểu đạt tình cảm kín đáo, ý nhị. Chọn C.
Câu 88:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Quyện điểu quy lâm tầm túc thụ
Cô vân mạn mạn độ thiên không
Sơn thôn thiếu nữ ma bao túc
Bao túc ma hoàn, lô dĩ hồng.
(Chiều tối – Hồ Chí Minh)
 Xem đáp án
Xem đáp án
Câu thơ “Cô vân mạn mạn độ thiên không” có nghĩa là chòm mây lẻ loi trôi lững lờ trên bầu trời. Chọn B.
Câu 89:
Đọc đoạn trích sau và trả lời câu hỏi:
Đêm trăng thanh anh mới hỏi nàng:
- Tre non đủ lá đan sàng nên chăng?
- Đan sàng thiếp cũng xin vâng,
Tre non đủ lá, nên chăng hỡi chàng?
(Ca dao)
 Xem đáp án
Xem đáp án
Bài ca dao sử dụng kết cấu đối đáp, là lời trò chuyện giữa đôi trai gái nhằm bày tỏ tình cảm của mình. Chọn C.
Câu 90:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Rượu, đến cội cây, ta sē uống,
Nhìn xem phú quý tựa chiêm bao.
(Nhàn – Nguyễn Bỉnh Khiêm)
 Xem đáp án
Xem đáp án
Hai câu thơ thể hiện nhân cách coi thường công danh phú quý của nhân vật trữ tình, coi phú quý cũng chỉ như giấc chiêm bao. Tác giả dùng từ “nhìn xem” thể hiện thế đứng cao hơn hẳn so với phú quý. Chọn B.
Câu 91:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trước muôn trùng sóng bể
Em nghĩ về anh, em
Em nghĩ về biển lớn
Từ nơi nào sóng lên?
- Sóng bắt đầu từ gió
Gió bắt đầu từ đâu?
Em cũng không biết nữa
Khi nào ta yêu nhau
(Sóng – Xuân Quỳnh)
 Xem đáp án
Xem đáp án
Ý chính của đoạn thơ thể hiện niềm suy tư, trăn trở của người phụ nữ trong tình yêu. Chọn D.
Câu 92:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Lều bạt chung chiêng giữa nước, giữa trời
Đến một cái gai cũng không sống được
Sớm mở mắt, nắng lùa ngun ngút
Đêm trong lều như trôi trong mây...
(Đồng đội tôi trên đảo Thuyền Chài, Trần Đăng Khoa)
 Xem đáp án
Xem đáp án
Nói quá: có thể hiểu là gai góc, cứng cỏi, sắc nhọn như cái gai mà cũng “không sống được” để nhấn mạnh điều kiện sống đầy khắc nghiệt và khổ cực của những người lính biển. Chọn A.
Câu 93:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Hỡi đồng bào cả nước,
“Tất cả mọi người sinh ra có quyền bình đẳng. Tạo hóa cho họ những quyền không ai có thể xâm phạm được; trong những quyền ấy, có quyền được sống, quyền tự do và quyền mưu cầu hạnh phúc.”
Lời bất hủ ấy ở trong bản Tuyên ngôn Độc lập năm 1776 của nước Mĩ. Suy rộng ra, câu ấy có ý nghĩa là: tất cả các dân tộc trên thế giới đều sinh ra bình đẳng, dân tộc nào cũng có quyền sống, quyền sung sướng và quyền tự do.
Bản Tuyên ngôn Nhân quyền và Dân quyền của Cách mạng Pháp năm 1791 cũng nói:
“Người ta sinh ra tự do và bình đẳng về quyền lợi, và phải luôn luôn được tự do và bình đẳng về quyền lợi.”
Đó là những lẽ phải không ai chối cãi được.
(Tuyên ngôn Độc lập – Hồ Chí Minh)
 Xem đáp án
Xem đáp án
Đoạn trích nói về cơ sở pháp lí của bản Tuyên ngôn của chủ tịch Hồ Chí Minh qua việc Người trích dẫn 2 bản Tuyên ngôn của Pháp và Mĩ. Chọn A.
Câu 94:
Đọc đoạn trích sau và trả lời câu hỏi:
Gì sâu bằng những trưa thương nhớ
Hiu quạnh bên trong một tiếng hò!
Đâu gió cồn thơm đất nhả mùi
Đâu ruồng tre mát thở yên vui
Đâu từng ô mạ xanh mơn mởn
Đâu những nương khoai ngọt sắn bùi?
(Nhớ đồng – Tố Hữu)
 Xem đáp án
Xem đáp án
Điệp ngữ “Đâu…”; nhân hóa “đất nhả mùi, ruồng tre mát thở yên vui…”. Chọn B.
Câu 95:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tiếng phong hạc phập phồng hơn mươi tháng, trông tin quan như trời hạn trông mưa; mùi tinh chiên vấy vá đã ba năm, ghét thói mọi như nhà nông ghét cỏ.
(Văn tế nghĩa sĩ Cần Giuộc – Nguyễn Đình Chiểu)
 Xem đáp án
Xem đáp án
Đoạn trích phản ánh sự thay đổi về phương diện tình cảm ở người nông dân khi nghe tin giặc Pháp xâm lược nước ta. Chọn A.
Câu 96:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Không những trong bộ lịch năm ấy mà mãi mãi về sau, tấm ảnh chụp của tôi vẫn còn được treo ở nhiều nơi, nhất là trong các gia đình sành nghệ thuật. Quái lạ, tuy là ảnh đen trắng nhưng mỗi lần ngắm kĩ, tôi vẫn thấy hiện lên cái màu hồng hồng của ánh sương mai lúc bấy giờ tôi nhìn thấy từ bãi xe tăng hỏng, và nếu nhìn lâu hơn, bao giờ tôi cũng thấy người đàn bà ấy đang bước ra khỏi tấm ảnh, đó là một người đàn bà vùng biển cao lớn với những đường nét thô kệch, tấm lưng áo bạc phếch có miếng vá, nửa thân dưới ướt sũng, khuôn mặt rỗ đã nhợt trắng vì kéo lưới suốt đêm. Mụ bước những bước chậm rãi, bàn chân giậm trên mặt đất chắc chắn, hòa lẫn trong đám đông…
(Chiếc thuyền ngoài xa – Nguyễn Minh Châu)
 Xem đáp án
Xem đáp án
“Màu hồng hồng của ánh sương mai” đó là ấn tượng đặc biệt về hiệu ứng màu sắc của Phùng lúc chụp ảnh, là niềm hân hoan khi anh phát hiện ra vẻ đẹp tuyệt đỉnh của ngoại cảnh; cũng là màu sắc thể hiện niềm tin vào tương lai của gia đình hàng chài nghèo khổ, đầy nghịch lí sống trên chiếc thuyền ấy. Chọn A.
Câu 97:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Bà lão cúi đầu nín lặng. Bà lão hiểu rồi. Lòng người mẹ nghèo khổ ấy còn hiểu ra biết bao nhiêu cơ sự, vừa ai oán vừa xót thương cho số kiếp đứa con mình. Chao ôi, người ta dựng vợ gả chồng cho con là lúc trong nhà ăn nên làm nổi, những mong sinh con đẻ cái mở mặt sau này. Còn mình thì... Trong kẽ mắt kèm nhèm của bà rủ xuống hai dòng nước mắt... Biết rằng chúng nó có nuôi nổi nhau sống qua được cơn đói khát này không?
(Vợ nhặt – Kim Lân)
 Xem đáp án
Xem đáp án
Những câu văn: Lòng người mẹ nghèo khổ ấy còn hiểu ra biết bao nhiêu cơ sự, vừa ai oán vừa xót thương cho số kiếp đứa con mình; Biết rằng chúng nó có nuôi nổi nhau sống qua được cơn đói khát này không thể hiện tâm trạng vừa lo lắng, vừa xót thương của bà cụ Tứ khi thấy Tràng dẫn người “vợ nhặt” về. Chọn A.
Câu 98:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Bữa cơm ngày đói trông thật thảm hại. Giữa cái mẹt rách có độc một lùm rau chuối thái rối, và một đĩa muối ăn với cháo, nhưng cả nhà đều ăn rất ngon lành. Bà cụ vừa ăn vừa kể chuyện làm ăn, gia cảnh với con dâu. Bà lão nói toàn chuyện vui, toàn chuyện sung sướng về sau này:
– Tràng ạ. Khi nào có tiền ta mua lấy đôi gà. Tao tin rằng cái chỗ đầu bếp kia làm cái chuồng gà thì tiện quá. Này ngoảnh đi ngoảnh lại chả mấy mà có ngay đàn gà cho mà xem...
(Vợ nhặt – Kim Lân)
 Xem đáp án
Xem đáp án
Trong lúc đói khổ khốn cùng mà bà cụ Tứ lại nói toàn chuyện vui, chuyện sung sướng về sau vì bà muốn nhen nhóm niềm vui, niềm hi vọng vào cuộc sống ngày mai. Chọn B.
Câu 99:
Đọc đoạn trích sau và trả lời câu hỏi:
Bảo Ninh là nhà văn đương đại nổi tiếng của Việt Nam; tên thật là Hoàng Ấu Phương, sinh năm 1952; quê gốc ở xã Bảo Ninh, thành phố Đồng Hới, tỉnh Quảng Bình; lớn lên và sống tại Hà Nội. Năm 17 tuổi, tốt nghiệp phổ thông (Trường Bưởi Chu Văn An), Bảo Ninh nhập ngũ, trở thành người lính (1969) và tham gia chiến đấu tại chiến trường B3 ác liệt (khu vực Tây Nguyên) cho đến tận khi chiến tranh kết thúc năm 1975.
Vốn là người lính từng trải nghiệm ở chiến trường ác liệt, nhiều truyện ngắn của Bảo Ninh thường bắt đầu bằng dòng kí ức đau thương trong chiến tranh, trong đó có truyện “Gọi con”. Truyện ngắn này được in trong tuyển tập “Truyện ngắn hay 2004”, sau đó được in trong tập “Chuyện xưa kết đi, được chưa?” (tập truyện ngắn, 2009). “Gọi con” cho người đọc thấm thía về “nỗi buồn chiến tranh” để từ đó, tri nhận đầy đủ về giá trị của cuộc sống hoà bình. Văn phong truyện ngắn Bảo Ninh thường đẹp mà buồn, có khi man mác dịu nhẹ, có khi day dứt sục sôi nhưng thường để lại trong bạn đọc những ám ảnh sâu sắc. “Gọi con” và một số truyện ngắn khác, cùng với tiểu thuyết “Nỗi buồn chiến tranh” khiến Bảo Ninh trở thành cây bút hàng đầu của mảng văn học chiến tranh thời hậu chiến và là cây bút thực sự sáng giá của văn học Việt Nam đương đại…
(Đọc hiểu mở rộng văn bản Ngữ văn 12)
 Xem đáp án
Xem đáp án
Đối tượng chính được đề cập đến trong đoạn trích là nhà văn Bảo Ninh. Chọn A.
Câu 100:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Em tưởng giếng sâu
Em nối sợi gầu dài
Ai ngờ giếng cạn
Em tiếc hoài sợi dây.
(Ca dao)
 Xem đáp án
Xem đáp án
Bài ca dao trên là tiếng lòng của người con gái. Cô tin tưởng rằng người con trai mình trao gửi cả cuộc đời là đẹp, là tốt song sự thật lại không như mong muốn. Chọn C.
Câu 101:
 Xem đáp án
Xem đáp án
Hai đại diện tiêu biểu cho khuynh hướng cứu nước mới-dân chủ tư sản ở Việt Nam những năm đầu thế kỉ XX là Phan Bội Châu và Phan Chu Trinh. Chọn B.
Câu 102:
 Xem đáp án
Xem đáp án
Giữa những năm 1970, Liên Xô là cường quốc công nghiệp thứ hai thế giới, đi đầu trong công nghiệp vũ trụ, công nghiệp điện hạt nhân...). Chọn A.
Câu 103:
 Xem đáp án
Xem đáp án
Từ nửa sau những năm 80 của thế kỉ XX, Nhật Bản vươn lên trở thành siêu cường tài chính số 1 thế giới, là chủ nợ lớn nhất thế giới. Chọn B.
Câu 104:
 Xem đáp án
Xem đáp án
Việc tách Đảng Cộng sản Đông Dương để thành lập Đảng Mác-Lênin riêng ở mỗi nước Việt Nam, Lào, Campuchia được quyết định tại Đại hội đại biểu lần thứ II của Đảng (2-1951). Chọn A.
Câu 105:
 Xem đáp án
Xem đáp án
A chọn vì ở Việt Nam lúc này tồn tại song song hai khuynh hướng dân chủ tư sản và vô sản. B loại vì ở Việt Nam lúc này tồn tại song song hai khuynh hướng dân chủ tư sản và vô sản nên nói hai khuynh hướng chính trị phát triển kế tiếp nhau là không đúng. Chọn A.
Câu 106:
 Xem đáp án
Xem đáp án
Dùng phương pháp loại trừ:
A loại vì chiến dịch Việt Bắc thu-đông (1947), Biên Giới thu-đông (1950), tiến công chiến lược đông xuân (1953 - 1954) không sử dụng chiến thuật hiệp đồng 3 thứ quân.
B chọn vì điểm chiến dịch Việt Bắc thu-đông (1947), Biên Giới thu-đông (1950), tiến công chiến lược đông xuân (1953 - 1954) và Điện Biên Phủ (1954) là đều kết hợp giữa chiến trường chính và vung sau lưng địch.
C loại vì khi tiến hành chiến dịch Việt Bắc, ta chưa có quyền chủ động trên chiến trường.
D loại vì chỉ trong chiến dịch Điện Biên Phủ (1954) ta mới đánh hiệp đồng binh chủng.
Chọn B.
Câu 107:
 Xem đáp án
Xem đáp án
Đảng Cộng sản Việt Nam ra đời là kết quả của cuộc đấu tranh dân tộc và giai cấp quyết liệt của nhân dân ta, là sự sàng lọc nghiêm khắc của lịch sử. Đảng ra đời là sản phẩm của sự kết hợp giữa chủ nghĩa Mác-Lê-nin, phong trào công nhân và phong trào yêu nước ở Việt Nam trong thời đại mới. Chọn B.
Câu 108:
 Xem đáp án
Xem đáp án
Để chuẩn bị tiến tới khởi nghĩa giành chính quyền, Đảng Cộng sản Đông Dương đã tích cực chuẩn bị lực lượng chính trị, lực lượng vũ trang, xây dựng căn cứ địa và tập dượt đấu tranh. Chọn C.
Câu 109:
 Xem đáp án
Xem đáp án
Bước sang năm 1941, những đội du Bắc Sơn lớn mạnh lên và thống nhất lại thành Trung đội Cứu quốc quân I (14-2-1941). Chọn D.
Câu 110:
 Xem đáp án
Xem đáp án
Năm 1944, Hội Văn hóa Cứu quốc được thành lập đã thu hút được đông đảo đội ngũ trí thức và những người hoạt động văn hóa, văn nghệ ưu tú nhất nước ta lúc bấy giờ, đưa họ đến với Mặt trận Việt Minh. Đây chính là minh chứng rõ nhất cho sự thành công trong thực tế của chiến lược đại đoàn kết dân tộc. Chọn A.
Câu 111:
 Xem đáp án
Xem đáp án
Kinh tế Mỹ La-tinh phát triển thiếu ổn định không phải do điều kiện tự nhiên khó khăn, ít tài nguyên thiên nhiên. Trái lại khu vực này giàu tài nguyên và điều kiện tự nhiên thuận lợi. Chọn C.
Câu 112:
 Xem đáp án
Xem đáp án
Biển của Nhật Bản có nguồn hải sản phong phú do có các ngư trường rộng lớn. Đây là nguyên nhân quan trọng nhất. Chọn D.
Câu 113:
 Xem đáp án
Xem đáp án
Vào mùa đông, gió mùa Đông Bắc ở miền Bắc nước ta thổi xen kẽ với gió tín phong Bán cầu Bắc. Chọn B.
Câu 114:
 Xem đáp án
Xem đáp án
Sự phân hóa thiên nhiên của vùng biển-thềm lục địa, vùng đồng bằng ven biển và vùng đồi núi là biểu hiện của sự phân hóa theo chiều đông-tây lần lượt. Phía đông là biển, rồi đến đồng bằng ở giữa và phía tây là đồi núi. Chọn B.
Câu 115:
 Xem đáp án
Xem đáp án
Đàn gia cầm của Quảng Nam trên 3 triệu con. Chọn A.
Câu 116:
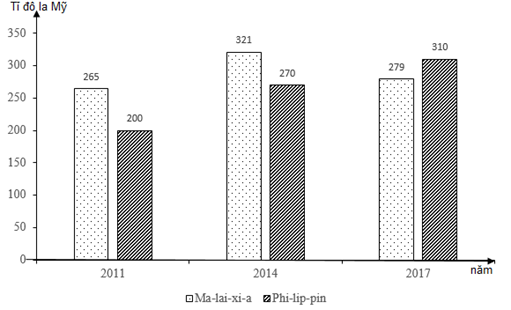
Cho biểu đồ GDP của Ma-lai-xi-a và Phi-lip-pin qua các năm
(Nguồn: Niến giám thống kê Việt Nam 2017, NXB Thống kê, 2019)
Biểu đồ thể hiện nội dung nào sau đây?
 Xem đáp án
Xem đáp án
Biểu đồ cột ghép, đơn vị GDP (tuyệt đối) → Biểu đồ đã cho thể hiện quy mô GDP của Ma-lai-xi-a và Phi-lip-pin. Chọn B.
Câu 117:
 Xem đáp án
Xem đáp án
Muốn xuất khẩu cần có thị trường → Chọn B.
A. đẩy mạnh khai thác khoáng sản các loại. → không chỉ khoáng sản còn nhiều sản phẩm khác
B. tích cực mở rộng thêm nhiều thị trường. → đúng
C. đẩy mạnh công nghiệp hóa và đô thị hóa. → thiếu yếu tố thị trường
D. tham gia của nhiều thành phần kinh tế. → thiếu yếu tố thị trường
Câu 118:
 Xem đáp án
Xem đáp án
Lao động nước ta có nhiều kinh nghiệm trong sản xuất nông nghiệp chứ không phải công nghiệp. Chọn B.
Câu 119:
 Xem đáp án
Xem đáp án
Tây Nguyên có thể trồng được cây chè là một loại cây cận nhiệt nhờ Khí hậu ở các cao nguyên trên 1000m mát mẻ. Chọn B.
Câu 120:
 Xem đáp án
Xem đáp án
Vấn đề có ý nghĩa hàng đầu đối với sự hình thành cơ cấu kinh tế của vùng Bắc Trung Bộ là hình thành cơ cấu nông-lâm-ngư nghiệp, do các ngành này tạo thành cơ cấu kinh tế liên hòa do đặc thù lãnh thổ. Chọn D.
Câu 121:
 Xem đáp án
Xem đáp án
Hiện tượng siêu dẫn là khi nhiệt độ hạ xuống dưới nhiệt độ \({T_c}\) nào đó thi điện trở của kim loại giảm đột ngột đến giá trị bằng không. Chọn A.
Câu 122:
 Xem đáp án
Xem đáp án
Khi đóng khóa K thì đèn 1 sáng lên ngay còn đèn 2 sáng lên từ từ. Chọn A.
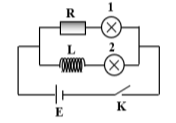
Câu 123:
 Xem đáp án
Xem đáp án
Ta có \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d^\prime }}} \to {d^\prime } = 60\;{\rm{cm}}{\rm{.}}\) Chọn A.
Câu 124:
 Xem đáp án
Xem đáp án
Sóng âm khi gặp con mồi sẽ bị phản xạ. Chọn B.
Câu 125:
 Xem đáp án
Xem đáp án
Trong chân không, các ánh sáng nhìn thấy được (ánh sáng khả kiến) có giá trị của bước sóng nằm trong giới hạn \(380\;{\rm{nm}} \le \lambda \le 760\;{\rm{nm}}.\) Chọn B.
Câu 126:
 Xem đáp án
Xem đáp án
Sau thời gian 5T, kể từ thời điểm ban đầu số hạt nhân chưa phân rã của mẫu chất phóng xạ này là \(N = {N_0}{.2^{ - \frac{t}{T}}} = \frac{1}{{32}}{N_0}\). Chọn A.
Câu 127:
 Xem đáp án
Xem đáp án
Ta có \(Li_1^2 + Cu_1^2 = Li_2^2 + Cu_2^2 \to {50.10^{ - 3}}.0,{16^2} + C{.5^2} = {50.10^{ - 3}}.0,{2^2} + C{.4^2} \to C = 80\mu F.\) Chọn D.
Câu 128:
 Xem đáp án
Xem đáp án
Ban đầu ta có \({x_M} = 5 \cdot \frac{{\lambda \cdot D}}{a}\)
Để tại \({\rm{M}}\) trở thành vân sáng bậc 2 thì \({x_M} = 2\frac{{\lambda {D^\prime }}}{a} = 2\frac{{\lambda (D + x)}}{a}\)
\( \Rightarrow 5\frac{{\lambda D}}{a} = 2\frac{{\lambda (D + x)}}{a} \Rightarrow 5 = 2 \cdot (1 + x) \Rightarrow x = 1,5\,m.\) Chọn A.
Câu 129:
Một con lắc lò xo treo vào một điểm cố định ở nơi có gia tốc trọng trường g = π2 (m/s2). Cho con lắc dao động điều hòa theo phương thẳng đứng. Hình bên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi Wđh của lò xo vào thời gian t. Khối lượng của con lắc gần nhất với giá trị nào sau đây?
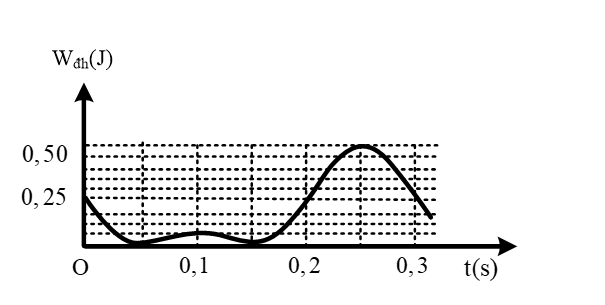
 Xem đáp án
Xem đáp án
\[{{\rm{W}}_{dh}} = \frac{1}{2}k\Delta {\ell ^2} = \frac{1}{2}m{\omega ^2}{\left( {\Delta {\ell _0} + x} \right)^2} \Rightarrow \left\{ \begin{array}{l}0,5625 = \frac{1}{2}m{\omega ^2}{\left( {\Delta {\ell _0} + A} \right)^2}\\0,0625 = \frac{1}{2}m{\omega ^2}{\left( {\Delta {\ell _0} - A} \right)^2}\end{array} \right.\]
Chọn C.
Câu 130:
Đặt điện áp xoay chiều có biểu thức \(u = {U_0}\cos \omega t\left( V \right)\)trong đó \({U_0},\omega \) không đổi vào hai đầu đoạn mạch gồm RLC nối tiếp, cuộn dây thuần cảm. Tại thời điểm \({t_1}\), điện áp tức thời ở hai đầu RLC lần lượt là \({u_R} = 50V,{u_L} = 30V,{u_C} = - 180V.\) Tại thời điểm \({t_2}\)các giá trị trên tương ứng là \({u_R} = 100V,{u_L} = {u_C} = 0V.\) Điện áp cực đại ở hai đầu đoạn mạch là:
Đáp án: ……….
 Xem đáp án
Xem đáp án
Tại \({t_2}\), ta có: \(\left\{ {\begin{array}{*{20}{c}}{{u_L} = {u_C} = 0}\\{{u_R} = 100V}\end{array}} \right.\) khi này \({u_{{R_{\max }}}} = {U_{0R}} = 100V\)
Tại \({t_1},\)ta có: \(\left\{ {\begin{array}{*{20}{c}}{{u_L} = 30V}\\{{u_C} = - 180V}\\{{u_R} = 50V}\end{array}} \right.\)
Ta có: \({u_L} \bot {u_R}\)ta suy ra: \({\left( {\frac{{{u_L}}}{{{U_{0L}}}}} \right)^2} + {\left( {\frac{{{u_R}}}{{{U_{0R}}}}} \right)^2} = 1\)\( \Rightarrow \frac{{{{30}^2}}}{{U_{0L}^2}} + \frac{{{{50}^2}}}{{{{100}^2}}} = 1 \Rightarrow {U_{0L}} = 20\sqrt 3 V\)
Lại có: \(\frac{{{U_{0L}}}}{{{U_{0C}}}} = \frac{{{Z_L}}}{{{Z_C}}} = - \frac{{{u_L}}}{{{u_C}}} = - \frac{{30}}{{\left( { - 180} \right)}} = \frac{1}{6}\)\( \Rightarrow {U_{0C}} = 120\sqrt 3 V\)
Điện áp cực đại ở hai đầu mạch: \({U_0} = \sqrt {{U_{0R}}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} = 200V\)
Đáp án: 200 V.
Câu 132:
Trong phòng thí nghiệm có 4 lọ hóa chất có dán nhãn tên hóa chất là: ethyl acetate, ethyl alcohol, acetic acid và methyl formate và 4 tờ đề can có ghi sẵn nhiệt độ sôi là: \(77{}^oC;\,32{}^oC;\,117,9{}^oC;\,\,78,3{}^oC\). Có một số phương án điền các giá trị nhiệt độ sôi tương ứng với các chất được trình bày trong bảng sau:
|
Chất |
methyl formate |
||||
|
Phương án |
1 |
\({77^o}C\) |
\(78,{3^o}C\) |
\(117,{9^o}C\) |
\({32^o}C\) |
|
2 |
\(78,{3^o}C\) |
\({32^o}C\) |
\({77^o}C\) |
\(117,{9^o}C\) |
|
|
3 |
\({32^o}C\) |
\(117,{9^o}C\) |
\(78,{3^o}C\) |
\({77^o}C\) |
|
|
4 |
\(117,{9^o}C\) |
\({77^o}C\) |
\({32^o}C\) |
\(78,{3^o}C\) |
|
Phương án đúng là
 Xem đáp án
Xem đáp án
Các chất ethyl alcohol \(\left( {{{\rm{C}}_2}{{\rm{H}}_5}{\rm{OH}}} \right)\), acetic acid \(\left( {{\rm{C}}{{\rm{H}}_3}{\rm{COOH}}} \right)\) và methyl fomate \(\left( {{\rm{HCOOC}}{{\rm{H}}_3}} \right)\) có cùng số C nên thứ tự nhiệt độ sôi theo thứ tự giảm dần là acid > alcohol > ester (*). Lưu ý: Nhiệt độ sôi ethyl acetate > methyl fomate do là ester có phân tử khối lớn hơn.
Chọn D.
Câu 133:
Một sinh viên thực hiện điện phân theo sơ đồ như dưới đây:
Sau một thời gian t điện phân, ở bình 2 xuất hiện 1,944 gam kim loại bạc bám trên điện cực. Biết trong hệ điện phân nối tiếp, số điện tử di chuyển qua các bình là bằng nhau. Giả sử kim loại được sinh ra bám toàn bộ trên điện cực. Số gam kim loại Zn bám trên điện cực là
 Xem đáp án
Xem đáp án
\({{\rm{n}}_{{\rm{Ag}}}} = \frac{{1,944}}{{108}} = 0,018\,(\;{\rm{mol}})\)
\(\begin{array}{l}{\rm{A}}{{\rm{g}}^ + } + 1{\rm{e}} \to {\rm{Ag}}\\\,\,\,\,\,\,\,\,\,\,\,0,018\quad 0,018\,\,\,\,\,\,\,mol\end{array}\)
Số điện tử di chuyển qua các bình là bằng nhau hay số mol electron thay đổi của \({\rm{A}}{{\rm{g}}^ + }\)và của \({\rm{Z}}{{\rm{n}}^{2 + }}\) là như nhau
\[\begin{array}{l}{\rm{Z}}{{\rm{n}}^{2 + }} + 2{\rm{e}} \to {\rm{Zn}}\\\,\,\,\,\,\,\,\,\,0,018 \to 0,009\,\,\,\,\,\,\,\;{\rm{mol}}\\ \Rightarrow {m_{Zn}} = 0,009.65{\rm{ }} = {\rm{ }}0,585{\rm{ }}gam.\end{array}\]
Chọn B.
Câu 134:
 Xem đáp án
Xem đáp án
- Thực hiện gộp quá trình ta có: \({{\rm{n}}_{{{\rm{H}}_2}{\rm{O}}}} = {{\rm{n}}_{{\rm{O}}{{\rm{H}}^ - }}} = 2{{\rm{n}}_X} + {{\rm{n}}_{{\rm{HCl}}}} = 0,2\;{\rm{mol}}\) và \({{\rm{n}}_{{\rm{KOH}}}} = {{\rm{n}}_{{\rm{NaOH}}}} = 0,1\;{\rm{mol}}\)
\( \Rightarrow {{\rm{M}}_X} = 133\) do đó \({\rm{n}} = 2.\) Công thức phân tử của X là \({C_4}{H_7}{O_4}N\).
Vậy \(\% {m_{C\,\,(X)}} = \frac{{12 \cdot 4}}{{133}} \cdot 100\% = 36,09\% .\)
Chọn C.
Câu 135:
Tiến hành thí nghiệm theo các bước sau để kiểm chứng tính chất của phenol.
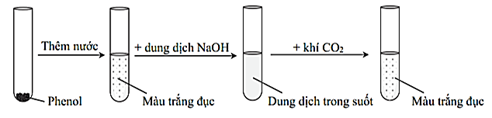
Phát biểu nào sau đây là sai?
 Xem đáp án
Xem đáp án
A, B, C. Đúng.
D. Sai, phenol không phản ứng với nước.
Phenol ít tan trong nước nên ban đầu thu được dung dịch có màu trắng đục.
Phenol tan hoàn toàn trong dung dịch\({\rm{NaOH}}\)nên khi thêm \({\rm{NaOH}}\) thu được dung dịch trong suốt:
\({{\rm{C}}_6}{{\rm{H}}_5}{\rm{OH}} + {\rm{NaOH}} \to {{\rm{C}}_6}{{\rm{H}}_5}{\rm{ONa}} + {{\rm{H}}_2}{\rm{O}}\)
Thêm \({\rm{C}}{{\rm{O}}_2}\) lại thu được dung dịch có màu trắng đục do xảy ra phản ứng
\({{\rm{C}}_6}{{\rm{H}}_5}{\rm{ONa}} + {{\rm{H}}_2}{\rm{O}} + {\rm{C}}{{\rm{O}}_2} \to {{\rm{C}}_6}{{\rm{H}}_5}{\rm{OH}} + {\rm{NaHC}}{{\rm{O}}_3}\)
(\({{\rm{H}}_2}{\rm{C}}{{\rm{O}}_3}\)có tính acid mạnh hơn \({{\rm{C}}_6}{{\rm{H}}_5}{\rm{OH}}\) nên đẩy được \({{\rm{C}}_6}{{\rm{H}}_5}{\rm{OH}}\) ra khỏi dung dịch muối). Phenol sinh ra ít tan trong nước nên thu được dung dịch có màu trắng đục. Chọn D.
Câu 136:
 Xem đáp án
Xem đáp án
Các polymer có nguồn gốc tự nhiên là cellulose, tơ tằm. Chọn A.
Câu 137:
 Xem đáp án
Xem đáp án
\({{\rm{n}}_{{\rm{N}}{{\rm{H}}_3}}} = 0,6\;{\rm{mol}};{{\rm{n}}_{{\rm{C}}{{\rm{O}}_2}}} = 0,5\;{\rm{mol}}\)
Gọi x, y lần lượt là số mol của \[N{H_4}HC{O_3}\]và \[{\left( {N{H_4}} \right)_2}C{O_3}\] trong hỗn hợp ban đầu
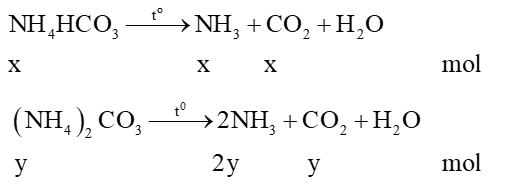
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 0,6}\\{x + y = 0,5}\end{array} \to \left\{ {\begin{array}{*{20}{l}}{x = 0,4}\\{y = 0,1}\end{array}} \right.} \right.\)(mol)
Khối lượng hỗn hợp ban đầu là: \({\rm{m}} = 0,4.79 + 0,1.96 = 41,2\) gam. Chọn C.
Câu 138:
Cho hình ảnh biểu thị sự phân li của acid có dạng HX (X là các gốc acid khác nhau) như hình dưới.
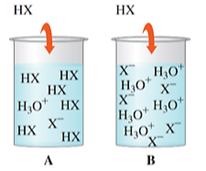
Phát biểu nào dưới đây không đúng?
 Xem đáp án
Xem đáp án
A. Đúng. Dung dịch A vẫn còn phân tử HX nên dung dịch trong cốc A là chất điện li yếu.
B. Đúng. Quan sát hình B thấy thành phần dung dịch chỉ chứa \({{\rm{H}}_3}{{\rm{O}}^ + }\)và \({{\rm{X}}^ - },\) vậy trong cốc B dung dịch HX phân li hoàn toàn.
C. Đúng do dung dịch cốc A vẫn còn phân tử HX.
D. Sai. Dung dịch B toàn bộ phân tử HX phân li thành các ion \({{\rm{H}}_3}{O^ + }\) và \({{\rm{X}}^ - }\) nên cốc B chứa chất điện li mạnh hay tính acid ở cốc B mạnh hơn.
Chọn D.
Câu 139:
Cho phản ứng giữa \({{\rm{H}}_2}(\;{\rm{g}})\) và \({{\rm{I}}_2}(\;{\rm{g}})\) trong một hệ cân bằng như sau:
Tiến hành trộn \({{\rm{H}}_2}(\;{\rm{g}})\) và \({{\rm{I}}_2}(\;{\rm{g}})\) với một lượng bằng nhau tạo thành hỗn hợp ở nhiệt độ \({\rm{T}}\) (điều kiện 1). Sự phụ thuộc của phần mol \({{\rm{I}}_2}(\;{\rm{g}})\) phụ thuộc theo thời gian được biểu diễn qua đồ thị hình bên.
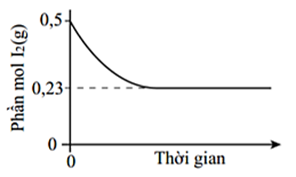
Thí nghiệm được lặp lại với nhiệt độ T nhưng bổ sung thêm chất xúc tác X (điều kiện 2). Đồ thị nào dưới đây biểu thị đúng sự phụ thuộc của phần \({\rm{mol}}\,\,{{\rm{I}}_2}(\;{\rm{g}})\) theo thời gian tại điều kiện 2 .
 Xem đáp án
Xem đáp án
Thêm chất xúc tác làm tốc độ phản ứng tăng Þ phản ứng nhanh đạt tới trạng thái cân bằng hơn nhưng lượng \({{\rm{I}}_2}\) tại thời điểm cân bằng vẫn không đổi Þ đáp án A (Tốc độ phản ứng tăng làm tăng độ dốc của đồ thị). Chọn C.
Câu 140:
Cho 60,8 gam hỗn hợp X gồm Cu, CuO và một oxide của sắt tác dụng với một lượng dung dịch HCl vừa đủ thu được dung dịch Y. Chia Y làm hai phần bằng nhau. Cho từ từ dung dịch \({{\rm{H}}_2}\;{\rm{S}}\) đến dư vào phần I thu được kết tủa Z. Hoà tan hết lượng kết tủa Z trong dung dịch \({\rm{HN}}{{\rm{O}}_3}\) đặc nóng, dư giải phóng 27,269 lít \({\rm{N}}{{\rm{O}}_2}\) (đkc, là sản phẩm khử duy nhất) và dung dịch \({\rm{T}}.\) Cho dung dịch T phản ứng với lượng dư dung dịch \({\rm{Ba}}{({\rm{OH}})_2}\) thu được m gam kết tủa. Mặt khác, phần II làm mất màu vừa đủ 500 ml dung dịch \({\rm{KMn}}{{\rm{O}}_4}0,44{\rm{M}}\) trong môi trường \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}.\) Giá trị của m là
Đáp án: ……….
 Xem đáp án
Xem đáp án
Tính ở \(\frac{1}{2}\)Y
Khi cho hỗn hợp X tác dụng với dung dịch HCl vừa đủ chỉ thu được dung dịch Y nên toàn bộ Cu đã phản ứng với muối \(F{e^{3 + }}\).
Quy đổi \(X\left\{ \begin{array}{l}CuO\,\,\,\,\,\,\,\,x\,mol\\FeO\,\,\,\,\,\,\,\,\,y\,mol\\F{e_2}{O_3}\,\,\,\,\,z\,mol\end{array} \right.\) (quy đổi theo sản phẩm)
Có khối lượng: \(80x + 72y + 160z = 30,4\) gam (1).
Chú ý: \({\rm{X}} + {\rm{HCl}} \to {\rm{Y}}\{ {\rm{CuC}}{{\rm{l}}_2};{\rm{FeC}}{{\rm{l}}_2};{\rm{FeC}}{{\rm{l}}_3});{\rm{Y}} + {{\rm{H}}_2}\;{\rm{S}} \to {\rm{x}}\) mol CuS \( \downarrow + {\rm{z}}\) mol \({\rm{S}} \downarrow .\)
(ở đây là \({\rm{2FeC}}{{\rm{l}}_3} + {{\rm{H}}_2}\;{\rm{S}} \to 2{\rm{FeC}}{{\rm{l}}_2} + {\rm{S}} \downarrow + 2{\rm{HCl}}\) ).
Þ Kết tủa Z là CuS (x mol) và S (z mol).
Theo đó, cho kết tủa Z: \({\rm{CuS}};{\rm{S}} + {\rm{HN}}{{\rm{O}}_3}\sinh \,ra\,\,1,1\;{\rm{mol}}\,\,{\rm{NO}}\)
Bảo toàn electron có: \(8{\rm{x}} + 6{\rm{z}} = 1,1\;{\rm{mol}}\,\,\,\,\,\,\,\,\,(2).\)
- Phần (II) làm mất màu dung dịch \(KMn{O_4}\)
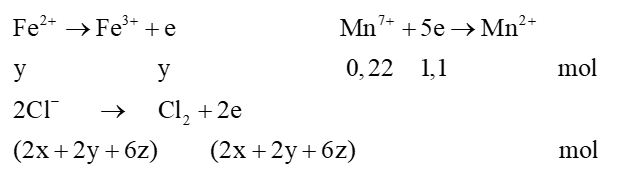
Bảo toàn electron lại có:
\(y + (2x + 2y + 6z) = 0,22 \cdot 5 \Rightarrow 2x + 3y + 6z = 1,1\;{\rm{mol}}\,\,\,\,\,(3).\)
Giải hệ (1); (2) và (3) được \(x = 0,1\;{\rm{mol}}\); y\( = 0,2\) mol và \(z = 0,05\) mol.
- Khi cho dung dịch T phản ứng với lượng dư dung dịch \(Ba{(OH)_2}\)thì có 2 phản ứng tạo kết tủa cần quan tâm sau:
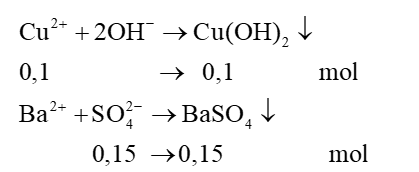
(Bảo toàn nguyên tố S ta có: \({n_{SO_4^{2 - }}} = x + z = 0,15\,mol\))
\( \to m = 0,1 \cdot 98 + 0,15 \cdot 233 = 44,75{\rm{ gam}}{\rm{. }}\)
Câu 141:
 Xem đáp án
Xem đáp án
Châu chấu có hình thức hô hấp bằng hệ thống ống khí, các loài còn lại hô hấp bằng mang. Chọn B.
Câu 142:
 Xem đáp án
Xem đáp án
Trên sợi trục có bao miêlin, xung thần kinh lan truyền theo cách nhảy cóc từ eo ranvie này sang eo ranvie khác. Nhờ đó, sự lan truyền xung thần kinh diễn ra nhanh chóng và ít tiêu tốn năng lượng hơn. Chọn C.
Câu 143:
 Xem đáp án
Xem đáp án
Không dùng auxin nhân tạo đối với nông phẩm trực tiếp làm thức ăn là vì auxin nhân tạo có thể tích lũy trong nông phẩm và gây độc hại đối với người và gia súc sử dụng. Chọn D.
Câu 144:
 Xem đáp án
Xem đáp án
D. Sai. Đột biến gen xảy ra một cách đột ngột và vô hướng nên không thể làm thay đổi tần số alen của quần thể theo một hướng xác định. Chọn D.
Câu 145:
 Xem đáp án
Xem đáp án
Ở sinh vật nhân thực, nhiễm sắc thể được cấu tạo từ chất nhiễm sắc bao gồm chủ yếu là ADN và prôtêin histôn. Chọn C.
Câu 146:
 Xem đáp án
Xem đáp án
Quần thể ở trạng thái cân bằng di truyền sẽ có cấu trúc di truyền là p2 AA : 2pq Aa : q2 aa → Tần số kiểu gen AA của quần thể trên là: 0,32 = 0,09. Chọn D.
Câu 147:
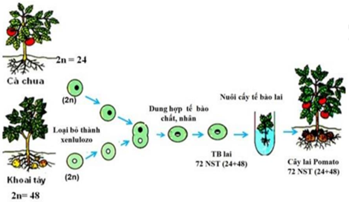
I. Đây là phương pháp dung hợp tế bào trần.
II. Đây là phương pháp gây đột biến.
III. Tạo được con lai mang 2 bộ NST khác nhau của 2 loài.
IV. Cây lai Pomato không có khả năng sinh sản hữu tính.
 Xem đáp án
Xem đáp án
Hình ảnh trên mô tả phương pháp dung hợp tế bào trần. Phương pháp này có thể tạo được con lai mang bộ NST của cả 2 loài mà bằng phương pháp lai hữu tính không thực hiện được. Vì con lai tạo ra bằng phương pháp này chứa cả 2 bộ NST lưỡng bội của 2 loài nên có khả năng sinh sản hữu tính. Vậy các nhận xét đúng là I, III. Chọn D.
Câu 148:
 Xem đáp án
Xem đáp án
Giao phối không ngẫu nhiên làm thay đổi thành phần kiểu gen nhưng không làm thay đổi tần số alen của quần thể. Giao phối ngẫu nhiên không làm thay đổi cả thành phần kiểu gen và tần số alen. Chọn A.
Câu 149:
Vườn cây ăn quả có loài rận chuyên đưa những con rệp lên chồi non, nhờ vậy rệp lấy được nhiều nhựa của cây ăn quả và thải ra chất dinh dưỡng cho loài rận ăn. Để đuổi loài rận, người nông dân đã thả vào vườn loài kiến ba khoang. Khi được thả vào vườn, kiến ba khoang tiêu diệt loài rận. Có bao nhiêu phát biểu sau đây đúng?
I. Kiến ba khoang và cam là quan hệ hợp tác.
II. Loài rận và cây ăn quả là quan hệ cạnh tranh.
III. Kiến ba khoang và loài rận là quan hệ sinh vật ăn sinh vật.
IV. Loài rận và rệp là quan hệ cộng sinh.
 Xem đáp án
Xem đáp án
I. Đúng. Vì kiến ba khoang ăn rệp cây nên cả kiến ba khoang và loài cây ăn quả đều được lợi.
II. Sai. Vì loài rận đã gián tiếp khai thác nhựa của cây ăn nên đây không phải là quan hệ cạnh tranh.
III. Đúng. Vì kiến ba khoang ăn loài rận.
IV. Đúng. Vì loài rận và rệp cây cùng hỗ trợ nhau một cách chặt chẽ để tồn tại.
Chọn C.
Câu 150:
Ở người, tính trạng nhóm máu do gen I nằm trên NST thường quy định. Gen I có 3 alen là IA, IB, IO, trong đó IA và IB đều trội so với IO nhưng không trội so với nhau. Người có kiểu gen IAIA hoặc IAIO có nhóm máu A; kiểu gen IBIB hoặc IBIO có nhóm máu B; kiểu gen IAIB có nhóm máu AB; kiểu gen IOIO có nhóm máu O. Xét phả hệ sau đây:
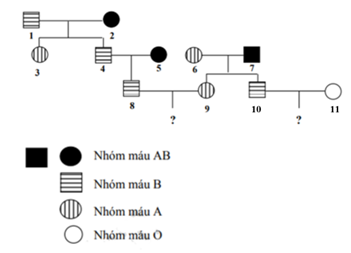
Theo lí thuyết, cặp vợ chồng 10 – 11 sinh con có nhóm máu O với xác suất là bao nhiêu phần trăm?
Đáp án: ……….
 Xem đáp án
Xem đáp án
- Người số 10 có nhóm máu B là con của người số 6 có nhóm máu A (IAI-) và người số 7 có nhóm máu AB (IAIB) → Người số 10 có kiểu gen IBIO.
- Người số 11 có nhóm máu O nên có kiểu gen là IOIO.
Vậy (10) × (11) → IBIO × IOIO → Cặp vợ chồng 10 – 11 sinh con có nhóm máu O với xác suất là 50%.
Đáp án: 50%.

