Giải bởi Vietjack
Không dùng auxin nhân tạo đối với nông phẩm trực tiếp làm thức ăn là vì auxin nhân tạo có thể tích lũy trong nông phẩm và gây độc hại đối với người và gia súc sử dụng. Chọn D.
Trong không gian \[Oxyz,\] cho đường thẳng \(d:\frac{{x - 1}}{3} = \frac{{y + 1}}{1} = \frac{z}{1}\) và mặt phẳng \(\left( P \right):2x + y - 2z + 2 = 0.\) Phương trình mặt cầu \(\left( S \right)\) có tâm nằm trên đường thẳng \(d\) có bán kính nhỏ nhất tiếp xúc với \(\left( P \right)\) và đi qua điểm \(A\left( {1\,;\,\, - 1\,;\,\,1} \right)\) là
Cho lăng trụ đứng tam giác có độ dài các cạnh đáy là \(37\,\;{\rm{cm}}\,,\,\,3\,\;{\rm{cm}}\,,\,\,30\;\,\;{\rm{cm}}\) và biết tổng diện tích các mặt bên là \(480\;\,{\rm{c}}{{\rm{m}}^2}.\) Thể tích \[V\] của lăng trụ đó là
Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 mét so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v\left( t \right) = 10t - {t^2}\), trong đó \(t\) (phút) là thời gian tính từ lúc bắt đầu chuyển động, \(v\left( t \right)\) được tính theo đơn vị mét/phút \(\left( {{\rm{m}}/{\rm{p}}} \right)\). Nếu như vậy thì khi bắt đầu tiếp xúc đất vận tốc \(v\) của khí cầu là
Cho hình ảnh biểu thị sự phân li của acid có dạng HX (X là các gốc acid khác nhau) như hình dưới.
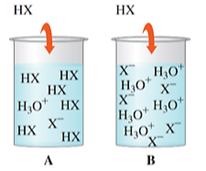
Phát biểu nào dưới đây không đúng?
Tìm giới hạn \(B = \mathop {\lim }\limits_{x \to 2} \frac{{{x^4} - 5{x^2} + 4}}{{{x^3} - 8}}.\)
Cho hình trụ có chiều cao bằng \(6\sqrt 2 \;\,{\rm{cm}}.\) Biết rằng một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song \(AB\,,\,\,A'B'\) mà \(AB = A'B' = 6\;\,{\rm{cm}}\), diện tích tứ giác \(ABB'A'\) bằng \(60\,\;{\rm{c}}{{\rm{m}}^{2.}}.\) Bán kính đáy của hình trụ bằng
Tỉnh A đưa ra nghị quyết về việc giảm biên chế công chức, viên chức hưởng lương từ ngân sách Nhà nước trong giai đoạn 5 năm từ 2020 – 2025 là \[12\% \] so với số lượng hiện có năm 2020. Giả sử tỉ lệ giảm hàng năm so với năm trước đó là như nhau. Để đạt được chỉ tiêu đề ra, tỉnh A phải thực hiện tỉ lệ giảm hàng năm tối thiểu là bao nhiêu phần trăm (làm tròn đến 1 chữ số thập phân)?
Một mảnh vườn hình chữ nhật có diện tích 961m2 người ta muốn mở rộng thêm 4 phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn. Biết tâm hình tròn trùng với tâm của hình chữ nhật. Tính diện tích nhỏ nhất của 4 phần đất được mở rộng (kết quả làm tròn đến chữ số hàng đơn vị).
Cho hình thang \[ABCD\] có \[AB\] song song \[CD\] và \(AB = AD = BC = a\,,\,\,CD = 2a.\) Thể tích của khối tròn xoay khi quay hình thang \[ABCD\] quanh trục \[AB\] bằng
Trong không gian Oxyz, cho hai điểm \[A\left( { - 2\,;\,\,3\,;\,\,4} \right),\,\,B\left( {8\,;\,\, - 5\,;\,\,6} \right).\] Hình chiếu vuông góc của trung điểm \[I\] của đoạn AB trên mặt phẳng \(\left( {Oyz} \right)\) là điểm nào dưới đây?
Trong không gian \[Oxyz,\] cho mặt cầu \((S):{x^2} + {y^2} + {z^2} + 4x - 6y + m = 0\) (\(m\) là tham số) và đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 4 + 2t}\\{y = 3 + t}\\{z = 3 + 2t}\end{array}} \right..\) Biết đường thẳng \(\Delta \) cắt mặt cầu \((S)\) tại hai điểm phân biệt \[A,\,\,B\] sao cho \(AB = 8.\) Giá trị của \(m\) là
Tìm giá trị thực của tham số \(m\) để hàm số \(y = \left( {m - 1} \right){x^4} - \left( {{m^2} - 2} \right){x^2} + 1\) đạt cực tiểu tại \(x = - 1.\)
Một vật chuyển động theo phương trình \(s\left( t \right) = \frac{1}{3}{t^3} - 2{t^2} + 4t\) với \(t\) (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và \[s\] (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Sau bao lâu thì chuyển động dừng lại?
Gọi \({z_1},\,\,{z_2}\) là hai nghiệm phức của phương trình \(\left( {z - i} \right)\left( {z + i} \right) = 2\left( {z - 3} \right).\) Giá trị của \(z_1^2 + z_2^2\) bằng
Có bao nhiêu tiếp tuyến của đồ thị hàm số \(y = \frac{{2x - 3}}{{x + 2}}\) đi qua giao điểm của hai đường tiệm cận của đồ thị hàm số đó?
