ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Phương trình lượng giác thường gặp
-
1253 lượt thi
-
27 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phương trình \[\sin 2x + 3\sin 4x = 0\] có nghiệm là:
 Xem đáp án
Xem đáp án
\[sin2x + 3sin4x = 0 \Leftrightarrow sin2x + 6sin2xcos2x = 0\]
\[ \Leftrightarrow sin2x(1 + 6cos2x) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sin2x = 0}\\{1 + 6cos2x = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sin2x = 0}\\{cos2x = - \frac{1}{6}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = k\pi }\\{2x = \pm arccos\left( { - \frac{1}{6}} \right) + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{k\pi }}{2}}\\{x = \pm \frac{1}{2}arccos( - \frac{1}{6}) + k\pi }\end{array}} \right.(k \in Z)\)
Đáp án cần chọn là: A
Câu 2:
Để phương trình \[\frac{{{a^2}}}{{1 - {{\tan }^2}x}} = \frac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}}\] có nghiệm, tham số a phải thỏa mãn điều kiện:
 Xem đáp án
Xem đáp án
\(\left\{ {\begin{array}{*{20}{c}}{1 - ta{n^2}x \ne 0}\\{cos2x \ne 0}\\{cosx \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{co{s^2}x - si{n^2}x}}{{co{s^2}x}}}\\{cos2x \ne 0}\\{cosx \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{cos2x \ne 0}\\{cosx \ne 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x \ne \frac{\pi }{2} + k\pi }\\{x \ne \frac{\pi }{2} + k\pi }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne \frac{\pi }{4} + \frac{{k\pi }}{2}}\\{x \ne \frac{\pi }{2} + k\pi }\end{array}} \right.(k \in Z)\)
\[\frac{{{a^2}}}{{1 - ta{n^2}x}} = \frac{{si{n^2}x + {a^2} - 2}}{{cos2x}}\]
\( \Leftrightarrow \frac{{{a^2}}}{{\frac{{co{s^2}x - si{n^2}x}}{{co{s^2}x}}}} = \frac{{si{n^2}x + {a^2} - 2}}{{cos2x}}\)
\( \Leftrightarrow \frac{{{a^2}co{s^2}x}}{{cos2x}} = \frac{{si{n^2}x + {a^2} - 2}}{{cos2x}}\)
\[ \Leftrightarrow {a^2}co{s^2}x = si{n^2}x + {a^2} - 2\]
\[ \Leftrightarrow {a^2}co{s^2}x = 1 - co{s^2}x + {a^2} - 2\]
\[ \Leftrightarrow ({a^2} + 1)co{s^2}x = {a^2} - 1 \Leftrightarrow co{s^2}x = \frac{{{a^2} - 1}}{{{a^2} + 1}} < 1\]
Vì \[\cos x \ne 0 \Rightarrow 0 < {\cos ^2}x \le 1 \Leftrightarrow {\cos ^2}x >0 \Leftrightarrow {a^2} - 1 >0 \Rightarrow \left| a \right| >1\]
Đáp án cần chọn là: B
Câu 3:
Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - y = \frac{\pi }{3}}\\{{\rm{cosx - }}\cos y = - 1}\end{array}} \right.\).
 Xem đáp án
Xem đáp án
Bước 1:
Bước 2:
Bước 3:
\[ \Rightarrow x = y + \frac{\pi }{3} = \frac{{2\pi }}{3} + k2\pi \left( {k \in Z} \right)\]
Vậy nghiệm của hệ phương trình là:\[\left( {x;y} \right) = \left( {\frac{{2\pi }}{3} + k2\pi ;\frac{\pi }{3} + k2\pi } \right)\,\,\,\left( {k \in Z} \right)\]
Đáp án cần chọn là: C
Câu 4:
Phương trình \[\sqrt 3 {\cot ^2}x - 4\cot x + \sqrt 3 = 0\]có nghiệm là:
 Xem đáp án
Xem đáp án
ĐK: \[\sin x \ne 0 \Leftrightarrow x \ne k\pi \,\,\left( {k \in Z} \right)\]
\[\sqrt 3 {\cot ^2}x - 4\cot x + \sqrt 3 = 0\]
Đặt cotx=t khi đó phương trình có dạng
\[\sqrt 3 {t^2} - 4t + \sqrt 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \frac{1}{{\sqrt 3 }}}\\{t = \sqrt 3 }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{cotx = \frac{1}{{\sqrt 3 }}}\\{cotx = \sqrt 3 }\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + k\pi }\\{x = \frac{\pi }{6} + k\pi }\end{array}} \right.(k \in Z)(tm)\)
Đáp án cần chọn là: A
Câu 5:
Phương trình \[{\sin ^2}3x + \left( {{m^2} - 3} \right)\sin 3x + {m^2} - 4 = 0\] khi m=1 có nghiệm là:
 Xem đáp án
Xem đáp án
Khi m=1 phương trình có dạng:\[{\sin ^2}3x - 2\sin 3x - 3 = 0\]
Đặt\[\sin 3x = t\,\,\left( { - 1 \le t \le 1} \right)\] khi đó phương trình có dạng
\[{t^2} - 2t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - 1(tm)}\\{t = 3(ktm)}\end{array}} \right.\]
\[t = - 1 \Leftrightarrow \sin 3x = - 1 \Leftrightarrow 3x = - \frac{\pi }{2} + k2\pi \Leftrightarrow x = - \frac{\pi }{6} + \frac{{k2\pi }}{3}\,\,\,\left( {k \in Z} \right)\]
Đáp án cần chọn là: C
Câu 6:
Nghiệm của phương trình \[4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\] là:
 Xem đáp án
Xem đáp án
Bước 1:
\[\begin{array}{*{20}{l}}{4{{\sin }^2}2x + 8{{\cos }^2}x - 9 = 0}\\{ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 8.\frac{{1 + \cos 2x}}{2} - 9 = 0}\\{ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4\left( {1 + \cos 2x} \right) - 9 = 0}\\{ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4 + 4\cos 2x - 9 = 0}\\{ \Leftrightarrow 4 - 4{{\cos }^2}2x + 4\cos 2x - 5 = 0}\\{ \Leftrightarrow - 4{{\cos }^2}2x + 4\cos 2x - 1 = 0}\end{array}\]
Bước 2:
Đặt \[\cos 2x = t\,\,\left( { - 1 \le t \le 1} \right)\] khi đó phương trình có dạng
\[ - 4{t^2} + 4t - 1 = 0 \Leftrightarrow - \left( {4{t^2} - 4t + 1} \right) = 0 \Leftrightarrow - {\left( {2t - 1} \right)^2} = 0 \Leftrightarrow t = \frac{1}{2}\left( {tm} \right)\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow \cos 2x = \frac{1}{2} \Leftrightarrow \cos 2x = \cos \frac{\pi }{3}}\\{ \Leftrightarrow 2x = \pm \frac{\pi }{3} + k2\pi \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi \left( {k \in Z} \right)}\end{array}\]
Đáp án cần chọn là: A
Câu 7:
Số vị trí biểu diễn các nghiệm của phương trình \[4{\sin ^2}x - 4\sin x - 3 = 0\]trên đường tròn lượng giác là:
 Xem đáp án
Xem đáp án
\[4{\sin ^2}x - 4\sin x - 3 = 0\]
Đặt\[\sin x = t\,\,\left( { - 1 \le t \le 1} \right)\]khi đó phương trình có dạng:
\[4{t^2} - 4t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \frac{3}{2}(ktm)}\\{t = - \frac{1}{2}(tm)}\end{array}} \right.\]
\[t = - \frac{1}{2} \Leftrightarrow sinx = - \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{6} + k2\pi }\\{x = - \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.(k \in Z)\]
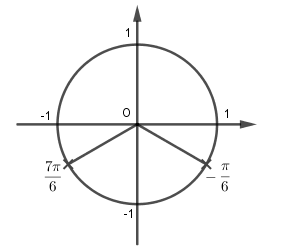
Vây số vị trí biểu diễn các nghiệm của phương trình\[4{\sin ^2}x - 4\sin x - 3 = 0\]trên đường tròn lượng giác là 2 điểm như hình trên.
Đáp án cần chọn là: C
Câu 8:
Với giá trị nào của m thì phương trình \[\sqrt 3 \sin 2x - m\cos 2x = 1\]luôn có nghiệm?
 Xem đáp án
Xem đáp án
\[\sqrt 3 \sin 2x - m\cos 2x = 1\]
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{b = \sqrt 3 }\\{b = - m}\\{c = 1}\end{array}} \right.\)
Để phương trình có nghiệm thì \[{a^2} + {b^2} \ge {c^2} \Leftrightarrow 3 + {m^2} \ge 1 \Leftrightarrow {m^2} \ge - 2\](luôn đúng với \[\forall m\])
Vậy phương trình luôn có nghiệm với mọi m.
Đáp án cần chọn là: D
Câu 9:
Phương trình \[\sqrt 3 \sin 2x - \cos 2x + 1 = 0\] có nghiệm là:
 Xem đáp án
Xem đáp án
\[\sqrt 3 sin2x - cos2x + 1 = 0\]
\[ \Leftrightarrow \frac{{\sqrt 3 }}{2}sin2x - \frac{1}{2}cos2x + \frac{1}{2} = 0\]
\[ \Leftrightarrow sin2x.cos\frac{\pi }{6} - cos2x.sin\frac{\pi }{6} = - \frac{1}{2}\]
\[ \Leftrightarrow sin(2x - \frac{\pi }{6}) = sin( - \frac{\pi }{6})\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x - \frac{\pi }{6} = - \frac{\pi }{6} + k2\pi }\\{2x - \frac{\pi }{6} = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = k2\pi }\\{2x = \frac{{4\pi }}{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{x = \frac{{2\pi }}{3} + k\pi }\end{array}} \right.(k \in \mathbb{Z})\)
Đáp án cần chọn là: D
Câu 10:
Khẳng định nào đúng về phương trình \[2\sqrt 2 \left( {\sin x + \cos x} \right)\cos x = 3 + \cos 2x\]
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{\,\,\,\,\,\,2\sqrt 2 \left( {\sin x + \cos x} \right)\cos x = 3 + \cos 2x}\\{ \Leftrightarrow 2\sqrt 2 \sin x\cos x + 2\sqrt 2 {{\cos }^2}x = 3 + \cos 2x}\\{ \Leftrightarrow \sqrt 2 \sin 2x + \sqrt 2 \left( {1 + \cos 2x} \right) = 3 + \cos 2x}\\{ \Leftrightarrow \sqrt 2 \sin 2x + \left( {\sqrt 2 - 1} \right)\cos 2x = 3 - \sqrt 2 }\end{array}\]
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{a = \sqrt 2 }\\{b = \sqrt 2 - 1}\\{c = 3 - \sqrt 2 }\end{array}} \right.\)
\[ \Rightarrow {a^2} + {b^2} - {c^2}\]
\[ = 2 + {(\sqrt 2 - 1)^2} - {(3 - \sqrt 2 )^2}\]
\[ = 2 + 3 - 2\sqrt 2 - 11 + 6\sqrt 2 \]
\[ = - 6 + 4\sqrt 2 < 0\]
\[ \Rightarrow {a^2} + {b^2} < {c^2}\]
Vậy phương trình vô nghiệm
Đáp án cần chọn là: C
Câu 11:
Phương trình \[\sin x + \sqrt 3 \cos x = \sqrt 2 \] có hai họ nghiệm có dạng \[x = \alpha + k2\pi ,x = \beta + k2\pi ,\]\[( - \frac{\pi }{2} < \alpha < \beta < \frac{\pi }{2})\;\]. Khi đó \[\alpha .\beta \;\] là:
 Xem đáp án
Xem đáp án
Bước 1:
\[\sin x + \sqrt 3 \cos x = \sqrt 2 \Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 2 }}{2}\]
\[\Leftrightarrow \sin x\cos \frac{\pi }{3} + \cos x\sin \frac{\pi }{3} = \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin \left( {x + \frac{\pi }{3}} \right) = \sin \frac{\pi }{4}\]
Bước 2:
\(\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + \frac{\pi }{3} = \frac{\pi }{4} + k2\pi }\\{x + \frac{\pi }{3} = \frac{\pi }{4} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{{12}} + k2\pi }\\{x = \frac{{5\pi }}{{12}} + k2\pi }\end{array}} \right.(k \in \mathbb{Z})\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\alpha = - \frac{\pi }{{12}}}\\{\beta = \frac{{5\pi }}{{12}}}\end{array}} \right.\)
(Vì\[ - \frac{\pi }{{12}}\] và\[\frac{{5\pi }}{{12}}\] đều thỏa mãn điều kiện đề bài)
\[ \Rightarrow \alpha .\beta \; = \frac{{ - 5{\pi ^2}}}{{144}}\]
Đáp án cần chọn là: B
Câu 12:
Số vị trí biểu diễn nghiệm của phương trình \[\sin x + \left( {\sqrt 3 - 2} \right)\cos x = 1\] trên đường tròn lượng giác là:
 Xem đáp án
Xem đáp án
Bước 1:
Với\[a = 1;b = \sqrt 3 - 2;c = 1\] ta có:
\[\begin{array}{*{20}{l}}{\sin x + \left( {\sqrt 3 - 2} \right)\cos x = 1}\\{ \Leftrightarrow \frac{1}{{\sqrt {8 - 4\sqrt 3 } }}\sin x + \frac{{\sqrt 3 - 2}}{{\sqrt {8 - 4\sqrt 3 } }}\cos x}\\{ = \frac{1}{{\sqrt {8 - 4\sqrt 3 } }}}\end{array}\]
Đặt \[\frac{1}{{\sqrt {8 - 4\sqrt 3 } }} = \cos \alpha \Rightarrow \frac{{\sqrt 3 - 2}}{{\sqrt {8 - 4\sqrt 3 } }} = \sin \alpha \] Khi đó phương trình tương đương:
\[\sin x\cos \alpha + \cos x\sin \alpha = \cos \alpha \]
Bước 2:
Vì \[\alpha \ne 0 \Rightarrow \]có 2 vị trí biểu diễn nghiệm của phương trình.
Đáp án cần chọn là: C
Câu 13:
Tổng các nghiệm thuộc đoạn \[\left[ {0;\frac{\pi }{2}} \right]\]của phương trình là:
 Xem đáp án
Xem đáp án
\[2\sqrt 3 cos2\frac{{5x}}{2} + sin5x = 1 + \sqrt 3 \; \Leftrightarrow \sqrt 3 (1 + cos5x) + sin5x = 1 + \sqrt 3 \]
\[ \Leftrightarrow sin5x + \sqrt 3 cos5x = 1 \Leftrightarrow \frac{1}{2}sin5x + \frac{{\sqrt 3 }}{2}cos5x = \frac{1}{2}\]
\[ \Leftrightarrow sin5xcos\frac{\pi }{3} + cos5xsin\frac{\pi }{3} = \frac{1}{2} \Leftrightarrow sin(5x + \frac{\pi }{3}) = sin\frac{\pi }{6}\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{5x + \frac{\pi }{3} = \frac{\pi }{6} + k2\pi }\\{5x + \frac{\pi }{3} = \frac{{5\pi }}{6} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{{30}} + \frac{{k2\pi }}{5}}\\{x = \frac{\pi }{{10}} + \frac{{k2\pi }}{5}}\end{array}} \right.(k \in \mathbb{Z})\)
Với họ nghiệm \[x = - \frac{\pi }{{30}} + \frac{{k2\pi }}{5}\,\,\left( {k \in \mathbb{Z}} \right)\]ta được
\[0 \le - \frac{\pi }{{30}} + \frac{{k2\pi }}{5} \le \frac{\pi }{2} \Leftrightarrow 0 \le - \frac{1}{{30}} + \frac{{2k}}{5} \le \frac{1}{2}\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{1}{{12}} \le k \le \frac{4}{3}}\\{k \in \mathbb{Z}}\end{array}} \right. \Rightarrow k = 1\)
\[ \Rightarrow x = - \frac{\pi }{{30}} + \frac{{2\pi }}{5} = \frac{{11\pi }}{{30}}\]
Với họ nghiệm \[x = \frac{\pi }{{10}} + \frac{{k2\pi }}{5}\,\,\left( {k \in \mathbb{Z}} \right)\]ta được:
\[0 \le \frac{\pi }{{10}} + \frac{{k2\pi }}{5} \le \frac{\pi }{2} \Leftrightarrow 0 \le \frac{1}{{10}} + \frac{{2k}}{5} \le \frac{1}{2}\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - \frac{1}{4} \le k \le 1}\\{k \in \mathbb{Z}}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{k = 0}\\{k = 1}\end{array}} \right.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{10}}}\\{x = \frac{\pi }{{10}} + \frac{{2\pi }}{5} = \frac{\pi }{2}}\end{array}} \right.\)
Vậy tổng các nghiệm thuộc đoạn\[\left[ {0;\frac{\pi }{2}} \right]\]là:\[\frac{{11\pi }}{{30}} + \frac{\pi }{{10}} + \frac{\pi }{2} = \frac{{29\pi }}{{30}}\]
Đáp án cần chọn là: B
Câu 14:
Phương trình \[{\sin ^3}x + {\cos ^3}x = \sin x - \cos x\] có nghiệm là:
 Xem đáp án
Xem đáp án
Bước 1:
\[\begin{array}{*{20}{l}}{{{\sin }^3}x + {{\cos }^3}x = \sin x - \cos x}\\{ \Leftrightarrow {{\cos }^3}x + \cos x = \sin x - {{\sin }^3}x}\\{ \Leftrightarrow \cos x\left( {{{\cos }^2}x + 1} \right) = \sin x\left( {1 - {{\sin }^2}x} \right)}\\{ \Leftrightarrow \cos x\left( {\frac{{1 + \cos 2x}}{2} + 1} \right) = \sin x.{{\cos }^2}x}\end{array}\]
\[\Leftrightarrow \cos x\left( {\frac{{1 + \cos 2x}}{2} + 1 - \sin x\cos x} \right) = 0\]
\[\begin{array}{*{20}{l}}{ \Leftrightarrow \cos x.\frac{{1 + \cos 2x + 2 - \sin 2x}}{2} = 0}\end{array}\]
\[\Leftrightarrow \cos x\left( {1 + \cos 2x + 2 - \sin 2x} \right) = 0\]
\[\Leftrightarrow \cos x\left( { - \sin 2x + \cos 2x + 3} \right) = 0\]
\(\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{cosx = 0(1)}\\{ - sin2x + cos2x + 3 = 0(2)}\end{array}} \right.\)
Bước 2:
\[\left( 1 \right) \Leftrightarrow x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\]
Xét (2) ta có:\(\left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = 1}\\{c = - 3}\end{array}} \right. \Rightarrow {a^2} + {b^2} < {c^2}\)
⇒⇒ phương trình (2) vô nghiệm.
Vậy nghiệm của phương trình là:\[x = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\]Đáp án cần chọn là: B
</>
Câu 15:
Phương trình \[6{\sin ^2}x + 7\sqrt 3 \sin 2x - 8{\cos ^2}x = 6\] có nghiệm là:
 Xem đáp án
Xem đáp án
\[6{\sin ^2}x + 7\sqrt 3 \sin 2x - 8{\cos ^2}x = 6 \Leftrightarrow 6{\sin ^2}x + 14\sqrt 3 \sin x\cos x - 8{\cos ^2}x = 6\,\left( * \right)\]
Trường hợp 1: \[\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \left( {k \in Z} \right)\]Khi đó\[{\sin ^2}x = 1\]Thay vào phương trình (*) ta có:\[6.1 + 14.0 - 8.0 = 6 \Leftrightarrow 6 = 6\] (luôn đúng)
\[ \Rightarrow x = \frac{\pi }{2} + k\pi \left( {k \in Z} \right)\]là nghiệm của phương trình.
Trường hợp 2: \[\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \left( {k \in Z} \right)\] Chia cả 2 vế của phương trình (*) cho \[{\cos ^2}x\]ta được:
\[\begin{array}{*{20}{l}}{6\frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} + 14\sqrt 3 \frac{{\sin x}}{{\cos x}} - 8 = \frac{6}{{{{\cos }^2}x}} \Leftrightarrow 6{{\tan }^2}x + 14\sqrt 3 \tan x - 8 = 6\left( {1 + {{\tan }^2}x} \right)}\\{ \Leftrightarrow 14\sqrt 3 \tan x - 14 = 0 \Leftrightarrow \sqrt 3 tanx - 1 = 0 \Leftrightarrow \tan x = \frac{1}{{\sqrt 3 }} \Leftrightarrow x = \frac{\pi }{6} + k\pi \left( {k \in Z} \right)}\end{array}\]
Kết hợp 2 trường hợp ta có nghiệm của phương trình là:\(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = \frac{\pi }{6} + k\pi }\end{array}} \right.(k \in Z)\)
Đáp án cần chọn là: A
Câu 16:
Trong khoảng \[\left( {0\,\,;\,\,\frac{\pi }{2}} \right)\]phương trình \[si{n^2}4x + 3sin4xcos4x - 4co{s^2}4x = 0\;\] có:
 Xem đáp án
Xem đáp án
Trường hợp 1:\[\cos 4x = 0 \Leftrightarrow 4x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\]
Khi đó\[{\sin ^2}4x = 1\]
Thay vào phương trình ta có:\[1 + 3.0 - 4.0 = 0 \Leftrightarrow 1 = 0\,\,\left( {V\^o \,\,l\'y } \right)\]
\[ \Rightarrow x = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\] không là nghiệm của phương trình.
Trường hợp 2:\[\cos 4x \ne 0 \Leftrightarrow x \ne \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\]
Chia cả 2 vế của phương trình cho \[{\cos ^2}4x\] ta được:
\[\frac{{{{\sin }^2}4x}}{{{{\cos }^2}4x}} + 3\frac{{\sin 4x}}{{\cos 4x}} - 4 = 0 \Leftrightarrow {\tan ^2}4x + 3\tan 4x - 4 = 0\]
Đặt tan4x=t. Khi đó phương trình trở thành
\[{t^2} + 3t - 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1}\\{t = - 4}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{tan4x = 1}\\{tan4x = - 4}\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = \frac{\pi }{4} + k\pi }\\{4x = arctan( - 4) + k\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{1}{4}arctan( - 4) + \frac{{k\pi }}{4}}\end{array}} \right.(k \in Z)\)
Xét nghiệm\[x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right),\,x \in \left( {0;\frac{\pi }{2}} \right)\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < \frac{\pi }{{16}} + \frac{{k\pi }}{4} < \frac{\pi }{2}}\\{k \in Z}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0 < \frac{1}{{16}} + \frac{k}{4} < \frac{1}{2}}\\{k \in Z}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - \frac{1}{4} < k < \frac{7}{4}}\\{k \in Z}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{k = 0}\\{k = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}}}\\{x = \frac{{5\pi }}{{16}}}\end{array}} \right.\)
Xét nghiệm\[x = \frac{1}{4}\arctan \left( { - 4} \right) + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right);\,\,x \in \left( {0;\frac{\pi }{2}} \right)\]
\(\left\{ {\begin{array}{*{20}{c}}{0 < \frac{1}{4}arctan( - 4) + \frac{{k\pi }}{4} < \frac{\pi }{2}}\\{k \in Z}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - \frac{1}{4}arctan( - 4) < \frac{{k\pi }}{4} < \frac{\pi }{2} - \frac{1}{4}arctan( - 4)}\\{k \in Z}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{0,42 < k < 2,42}\\{k \in Z}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{k = 1}\\{k = 2}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{1}{4}arctan( - 4) + \frac{\pi }{4}}\\{x = \frac{1}{4}arctan( - 4) + \frac{\pi }{2}}\end{array}} \right.\)
Vậy phương trình có 4 nghiệm thuộc khoảng\[\left( {0\,\,;\,\,\frac{\pi }{2}} \right)\]
Đáp án cần chọn là: D
Câu 17:
Có bao nhiêu giá trị m nguyên để phương trình \[si{n^2}x - msinxcosx - 3co{s^2}x = 2m\] có nghiệm?
 Xem đáp án
Xem đáp án
Trường hợp 1: \[\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\] Khi đó \[{\sin ^2}x = 1\]Thay vào phương trình ta có:\[1 - m.0 - 3.0 = 2m\, \Leftrightarrow 2m = 1 \Leftrightarrow m = \frac{1}{2} \notin Z \Rightarrow \] loại
Trường hợp 2:\[\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\]
Chia cả 2 vế của phương trình cho\[{\cos ^2}x\] ta được:
\[\begin{array}{*{20}{l}}{\frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} - m\frac{{\sin x}}{{\cos x}} - 3 = \frac{{2m}}{{{{\cos }^2}x}}}\\{ \Leftrightarrow {{\tan }^2}x - m\tan x - 3 = 2m\left( {1 + {{\tan }^2}x} \right)}\\{ \Leftrightarrow \left( {2m - 1} \right){{\tan }^2}x + m\tan x + 2m + 3 = 0}\end{array}\]Đặt tanx = t khi đó phương trình có dạng\[\left( {2m - 1} \right){t^2} + mt + 2m + 3 = 0\]
\[m = \frac{1}{2} \notin Z \Rightarrow \] loại
\[m \ne \frac{1}{2}\] ta có:\[{\rm{\Delta }} = {m^2} - 4\left( {2m - 1} \right)\left( {2m + 3} \right) = {m^2} - 16{m^2} - 16m + 12 = - 15{m^2} - 16m + 12\]
Để phương trình có nghiệm thì\[{\rm{\Delta }} \ge 0 \Leftrightarrow \frac{{ - 8 - 2\sqrt {61} }}{{15}} \le m \le \frac{{ - 8 + 2\sqrt {61} }}{{15}}\]
Mà\[m \in Z \Rightarrow \left\{ {\begin{array}{*{20}{c}}{m = - 1}\\{m = 0}\end{array}} \right.\]
Đáp án cần chọn là: C
Câu 18:
Các giá trị nguyên dương nhỏ hơn 5 của m để phương trình \[\tan x + \cot x = m\] có nghiệm \[x \in (0;\frac{\pi }{2})\;\] có tổng là:
 Xem đáp án
Xem đáp án
Với \[x \in \left( {0;\frac{\pi }{2}} \right)\] ta có:\(\left\{ {\begin{array}{*{20}{c}}{sinx >0}\\{cosx >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{tanx >0}\\{cotx >0}\end{array}} \right.\)
Ta có:\[\tan x + \cot x = \tan x + \frac{1}{{\tan x}} \ge 2\sqrt {\tan x.\frac{1}{{\tan x}}} = 2\] (BĐT Cauchy)
Phương trình có nghiệm\[ \Leftrightarrow m \ge 2\]
Kết hợp điều kiện ta có:\(\left\{ {\begin{array}{*{20}{c}}{2 \le m < 5}\\{m \in {Z^ + }}\end{array}} \right. \Rightarrow m \in \{ 2;3;4\} \)
Vậy tổng các giá trị của m thỏa mãn là 2+3+4=9
Đáp án cần chọn là: A
Câu 19:
Với giá trị nào của m thì phương trình \[\left( {1 - m} \right){\tan ^2}x - \frac{2}{{\cos x}} + 1 + 3m = 0\]có nhiều hơn 1 nghiệm trên \[(0;\frac{\pi }{2})\;\]?
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{\left( {1 - m} \right){{\tan }^2}x - \frac{2}{{\cos x}} + 1 + 3m = 0}\\{ \Leftrightarrow \left( {1 - m} \right)\frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} - \frac{2}{{\cos x}} + 1 + 3m = 0}\\{ \Leftrightarrow \left( {1 - m} \right){{\sin }^2}x - 2\cos x + \left( {1 + 3m} \right){{\cos }^2}x = 0}\\{ \Leftrightarrow \left( {1 - m} \right)\left( {1 - {{\cos }^2}x} \right) - 2\cos x + \left( {1 + 3m} \right){{\cos }^2}x = 0}\\{ \Leftrightarrow 4m{{\cos }^2}x - 2\cos x + 1 - m = 0}\end{array}\]
Đặt t=cosx
Vì \[x \in \left( {0;\frac{\pi }{2}} \right) \Rightarrow t \in \left( {0;1} \right)\]khi đó phương trình trở thành
\[4m{t^2} - 2t + 1 - m = 0(1)\]
\[ \Leftrightarrow m(4{t^2} - 1) - (2t - 1) = 0\]
\[ \Leftrightarrow m(2t + 1)(2t - 1) - (2t - 1) = 0\]
\[ \Leftrightarrow (2t - 1)(2mt + m - 1) = 0\]
\(\left[ {\begin{array}{*{20}{c}}{t = \frac{1}{2} \in (0;1)}\\{2mt = 1 - m(2)}\end{array}} \right.\)
Để phương trình ban đầu có nhiều hơn 1 nghiệm thuộc\[\left( {0;\frac{\pi }{2}} \right)\]thì phương trình (1)(1) có nhiều hơn 1 nghiệm thuộc (0;1). Khi đó phương trình (2) có nghiệm thuộc\[\left( {0;1} \right) \setminus \left\{ {\frac{1}{2}} \right\}\]
Khi m=0 ta có 0t=1 (vô nghiệm)
Khi \[m \ne 0\]thì \[\left( 2 \right) \Leftrightarrow t = \frac{{1 - m}}{{2m}}\]
Để phương trình (2) có nghiệm thuộc\[\left( {0;1} \right) \setminus \left\{ {\frac{1}{2}} \right\}\] thì
\(\left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{0 < \frac{{1 - m}}{{2m}} < 1}\\{\frac{{1 - m}}{{2m}} \ne \frac{1}{2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{\frac{{1 - m}}{{2m}} >0}\\{\frac{{1 - m}}{{2m}} < 1}\\{2(1 - m) \ne 2m}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{\frac{{1 - m}}{{2m}} >0}\\{\frac{{1 - 3m}}{{2m}} < 0}\\{4m \ne 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ne 0}\\{0 < m < 1}\\{\left[ {\begin{array}{*{20}{c}}{m < 0}\\{m >\frac{1}{3}}\end{array}} \right.}\\{m \ne \frac{1}{2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{1}{3} < m < 1}\\{m \ne \frac{1}{2}}\end{array}} \right.\)
Đáp án cần chọn là: C
Câu 20:
Giải phương trình \[\sqrt 3 \cos 5x - 2\sin 3x\cos 2x - \sin x = 0\] ta được nghiệm:
 Xem đáp án
Xem đáp án
\[\begin{array}{l}\sqrt 3 cos5x - 2sin3xcos2x - sinx = 0\\ \Leftrightarrow \sqrt 3 cos5x - (sin5x + sinx) - sinx = 0\end{array}\]
\[ \Leftrightarrow \sqrt 3 cos5x - sin5x = 2sinx\]
\[ \Leftrightarrow \frac{{\sqrt 3 }}{2}cos5x - \frac{1}{2}sin5x = sinx\]
\[ \Leftrightarrow sin\frac{\pi }{3}cos5x - cos\frac{\pi }{3}sin5x = sinx\]
\[ \Leftrightarrow sin(\frac{\pi }{3} - 5x) = sinx\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{\pi }{3} - 5x = x + k2\pi }\\{\frac{\pi }{3} - 5x = \pi - x + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{18}} + \frac{{k\pi }}{3}}\\{x = - \frac{\pi }{6} + \frac{{k\pi }}{2}}\end{array}} \right.(k \in \mathbb{Z})\)
Vậy nghiệm của phương trình là \[x = \frac{\pi }{{18}} + \frac{{k\pi }}{3};\,\,x = - \frac{\pi }{6} + \frac{{k\pi }}{2}\,\,\left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: D
Câu 21:
Giải phương trình \[\cos x\cos \frac{x}{2}\cos \frac{{3x}}{2} - \sin x\sin \frac{x}{2}\sin \frac{{3x}}{2} = \frac{1}{2}\]
 Xem đáp án
Xem đáp án
\[\cos x\cos \frac{x}{2}\cos \frac{{3x}}{2} - \sin x\sin \frac{x}{2}\sin \frac{{3x}}{2} = \frac{1}{2}\]
\[ \Leftrightarrow \frac{1}{2}cosx(cos2x + cosx) + \frac{1}{2}sinx(cos2x - cosx) = \frac{1}{2}\]
\[ \Leftrightarrow cosxcos2x + co{s^2}x + sinxcos2x - sinxcosx = 1\]
\[ \Leftrightarrow cos2x(sinx + cosx) - sinxcosx + co{s^2}x - 1 = 0\]
\[ \Leftrightarrow cos2x(sinx + cosx) - sinxcosx - si{n^2}x = 0\]
\[ \Leftrightarrow cos2x(sinx + cosx) - sinx(sinx + cosx) = 0\]
\[ \Leftrightarrow (sinx + cosx)(cos2x - sinx) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sinx + cosx = 0}\\{cos2x - sinx = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sinx = - cosx}\\{1 - 2si{n^2}x - sinx = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{tanx = - 1}\\{sinx = \frac{1}{2}}\\{sinx = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{4} + k\pi }\\{x = \frac{\pi }{6} + k2\pi }\\{x = \frac{{5\pi }}{6} + k2\pi }\\{x = - \frac{\pi }{2} + k2\pi }\end{array}} \right.(k \in \mathbb{Z})\)
Vậy nghiệm của phương trình đã cho là: \[x = - \frac{\pi }{4} + k\pi ;\,\,x = \frac{\pi }{6} + k2\pi ;x = \frac{{5\pi }}{6} + k2\pi ;\,\,x = - \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: A
Câu 22:
Giải phương trình \[\cos 2x + \cos 4x + \cos 6x = \cos x\cos 2x\cos 3x + 2\]
 Xem đáp án
Xem đáp án
\[cos2x + cos4x + cos6x = cosxcos2xcos3x + 2\]
\[ \Leftrightarrow 2cos4xcos2x + cos4x = \frac{1}{2}cos2x(cos4x + cos2x) + 2\]
\[ \Leftrightarrow 2cos4xcos2x + cos4x = \frac{1}{2}cos2xcos4x + \frac{1}{2}co{s^2}2x + 2\]
\[ \Leftrightarrow \frac{3}{2}cos4xcos2x + cos4x = \frac{1}{2}co{s^2}2x + 2\]
\[ \Leftrightarrow 3cos4xcos2x + 2cos4x = co{s^2}2x + 4\]
\[ \Leftrightarrow 3(2co{s^2}2x - 1)cos2x + 2(2co{s^2}2x - 1) = co{s^2}2x + 4\]
\[ \Leftrightarrow 6co{s^3}2x - 3cos2x + 4co{s^2}2x - 2 = co{s^2}2x + 4\]
\[ \Leftrightarrow 6co{s^3}2x + 3co{s^2}2x - 3cos2x - 6 = 0\]
\[ \Leftrightarrow 2co{s^3}2x + co{s^2}2x - cos2x - 2 = 0\]
\[ \Leftrightarrow 2(co{s^3}2x - 1) + cos2x(cos2x - 1) = 0\]
\[ \Leftrightarrow 2(cos2x - 1)(co{s^2}2x + cos2x + 1) + cos2x(cos2x - 1) = 0\]
\[ \Leftrightarrow (cos2x - 1)(2co{s^2}2x + 2cos2x + 2 + cos2x) = 0\]
\[ \Leftrightarrow (cos2x - 1)(2co{s^2}2x + 3cos2x + 2) = 0\]
\[ \Leftrightarrow cos2x = 1 \Leftrightarrow 2x = k2\pi \Leftrightarrow x = k\pi (k \in \mathbb{Z})\]
Vậy nghiệm của phương trình đã cho là: \[x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: A
Câu 23:
Giải phương trình \[\cos 3x\tan 5x = \sin 7x\]
 Xem đáp án
Xem đáp án
ĐKXĐ: \[\cos 5x \ne 0 \Leftrightarrow 5x \ne \frac{\pi }{2} + m\pi \Leftrightarrow x \ne \frac{\pi }{{10}} + \frac{{m\pi }}{5}\,\,\left( {m \in \mathbb{Z}} \right)\]
\[cos3xtan5x = sin7x\]
\[ \Leftrightarrow cos3xsin5x = sin7xcos5x\]
\[ \Leftrightarrow \frac{1}{2}(sin8x + sin2x) = \frac{1}{2}(sin12x + sin2x)\]
\[ \Leftrightarrow sin8x + sin2x = sin12x + sin2x\]
\[ \Leftrightarrow sin12x = sin8x\]
\(\left[ {\begin{array}{*{20}{c}}{12x = 8x + k2\pi }\\{12x = \pi - 8x + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{k\pi }}{2}}\\{x = \frac{\pi }{{20}} + \frac{{k\pi }}{{10}}}\end{array}} \right.(k \in \mathbb{Z})\)
Đối chiếu điều kiện ta có:
\[\begin{array}{*{20}{l}}{\,\,\,\,\,\,\frac{{k\pi }}{2} \ne \frac{\pi }{{10}} + \frac{{m\pi }}{5}\,\,\left( {k,\,\,m \in \mathbb{Z}} \right)}\\{ \Leftrightarrow 5k \ne 1 + 2m}\\{ \Leftrightarrow k \ne \frac{{1 + 2m}}{5}}\end{array}\]
Do \[k \in \mathbb{Z}\] nên:\[k = \frac{{1 + 2m}}{5} \Leftrightarrow \frac{{1 + 2m}}{5}\] là số nguyên. Mà 1+2m luôn lẻ nên\[\frac{{1 + 2m}}{5}\] không chia hết cho 2 với mọi m. Do đó, nếu\[k \ne \frac{{1 + 2m}}{5}\] thì k phải là số nguyên chẵn.
⇒kchẵn, đặt k=2n, khi đó ta có \[x = \frac{{2n\pi }}{2} = n\pi \left( {n \in \mathbb{Z}} \right)\]
\[\begin{array}{*{20}{l}}{\,\,\,\,\,\,\frac{\pi }{{20}} + \frac{{k\pi }}{{10}} \ne \frac{\pi }{{10}} + \frac{{m\pi }}{5}\,\,\left( {k,\,\,m \in \mathbb{Z}} \right)}\\{ \Leftrightarrow 1 + 2k \ne 2 + 4m}\end{array}\]
Vì\[1 + 2k\] lẻ,\[2 + 4m\] chẵn nên\[1 + 2k \ne 2 + 4m\] luôn đúng với mọi\[k,\,\,m \in \mathbb{Z}\]
Vậy nghiệm của phương trình đã cho là:\[x = n\pi ;\,\,x = \frac{\pi }{{20}} + \frac{{k\pi }}{{10}}\,\,\left( {k,\,\,n \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: B
Câu 24:
Giải phương trình \[\sin 3x - \frac{2}{{\sqrt 3 }}{\sin ^2}x = 2\sin x\cos 2x\].
 Xem đáp án
Xem đáp án
\[\sin 3x - \frac{2}{{\sqrt 3 }}{\sin ^2}x = 2\sin x\cos 2x\]
\[ \Leftrightarrow \sqrt 3 sin3x - 2si{n^2}x = \sqrt 3 (sin3x - sinx)\]
\[ \Leftrightarrow \sqrt 3 sin3x - 2si{n^2}x = \sqrt 3 sin3x - \sqrt 3 sinx\]
\[ \Leftrightarrow 2si{n^2}x - \sqrt 3 sinx = 0\]
\[ \Leftrightarrow sinx(2sinx - \sqrt 3 ) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sinx = 0}\\{sinx = \frac{{\sqrt 3 }}{2}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{x = \frac{\pi }{3} + k2\pi }\\{x = \frac{{2\pi }}{3} + k2\pi }\end{array}} \right.(k \in \mathbb{Z})\)
Vậy nghiệm của phương trình đã cho là:
\[x = k\pi ;\,\,x = \frac{\pi }{3} + k2\pi ;\,\,x = \frac{{2\pi }}{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: C
Câu 25:
Giải phương trình \[\sin 18x\cos 13x = \sin 9x\cos 4x\]
 Xem đáp án
Xem đáp án
\[\sin 18x\cos 13x = \sin 9x\cos 4x\]
\[ \Leftrightarrow \frac{1}{2}(sin31x + sin5x) = \frac{1}{2}(sin13x + sin5x)\]
\[ \Leftrightarrow sin31x + sin5x = sin13x + sin5x\]
\[ \Leftrightarrow sin31x = sin13x\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{31x = 13x + k2\pi }\\{31x = \pi - 13x + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{18x = k2\pi }\\{44x = \pi + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{k\pi }}{9}}\\{x = \frac{\pi }{{44}} + \frac{{k\pi }}{{22}}}\end{array}} \right.(k \in \mathbb{Z})\)
Vậy nghiệm của phương trình là\[x = \frac{{k\pi }}{9};\,\,x = \frac{\pi }{{44}} + \frac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: B
Câu 26:
Giải phương trình \[1 + \sin x + \cos 3x = \cos x + \sin 2x + \cos 2x\]
 Xem đáp án
Xem đáp án
\[1 + \sin x + \cos 3x = \cos x + \sin 2x + \cos 2x\]
\[ \Leftrightarrow (1 - cos2x) + (sinx - sin2x) + (cos3x - cosx) = 0\]
\[ \Leftrightarrow 2si{n^2}x + (sinx - sin2x) - 2sin2xsinx = 0\]
\[ \Leftrightarrow 2sinx(sinx - sin2x) + (sinx - sin2x) = 0\]
\[ \Leftrightarrow (sinx - sin2x)(2sinx + 1) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sin2x = sinx}\\{sinx = - \frac{1}{2}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = x + k2\pi }\\{2x = \pi - x + k2\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k2\pi }\\{x = \frac{\pi }{3} + \frac{{k2\pi }}{3}}\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.\)
Vậy nghiệm của phương trình là:\[x = k2\pi ,x = \frac{\pi }{3} + \frac{{k2\pi }}{3},x = - \frac{\pi }{6} + k2\pi ,x = \frac{{7\pi }}{6} + k2\pi \]
Đáp án cần chọn là: B
Câu 27:
Giải phương trình \[\cos x + \cos 3x + 2\cos 5x = 0\]
 Xem đáp án
Xem đáp án
\[\cos x + \cos 3x + 2\cos 5x = 0\]
\[ \Leftrightarrow cosx + cos3x + cos5x + cos5x = 0\]
\[ \Leftrightarrow (cosx + cos5x) + (cos3x + cos5x) = 0\]
\[ \Leftrightarrow 2cos3xcos2x + 2cos4xcosx = 0\]
\[ \Leftrightarrow 2(4co{s^3}x - 3cosx)cos2x + 2cos4xcosx = 0\]
\[ \Leftrightarrow 2cosx(4co{s^2}x - 3)cos2x + 2cos4xcosx = 0\]
\[ \Leftrightarrow 2cosx[(4co{s^2}x - 3)cos2x + cos4x] = 0\]
\[ \Leftrightarrow 2cosx[[2(1 + cos2x) - 3]cos2x + 2co{s^2}2x - 1] = 0\]
\[ \Leftrightarrow 2cosx[(2cos2x - 1)cos2x + 2co{s^2}2x - 1] = 0\]
\[ \Leftrightarrow 2cosx[4co{s^2}2x - cos2x - 1] = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{cosx = 0}\\{cos2x = \frac{{1 + \sqrt {17} }}{8}}\\{cos2x = \frac{{1 - \sqrt {17} }}{8}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{2x = \pm arccos\frac{{1 + \sqrt {17} }}{8} + k2\pi }\\{2x = \pm arccos\frac{{1 - \sqrt {17} }}{8} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = \pm \frac{1}{2}arccos\frac{{1 + \sqrt {17} }}{8} + k\pi }\\{x = \pm \frac{1}{2}arccos\frac{{1 - \sqrt {17} }}{8} + k\pi }\end{array}} \right.\)
Vậy nghiệm của phương trình là: \[x = \frac{\pi }{2} + k\pi ,x = \pm \frac{1}{2}\arccos \frac{{1 + \sqrt {17} }}{8} + k\pi ,x = \pm \frac{1}{2}\arccos \frac{{1 - \sqrt {17} }}{8} + k\pi \]
Đáp án cần chọn là: DCâu 32. Giải phương trình \[\sin 3x - \sin x + \sin 2x = 0\]
A.\[x = k\pi ,x = \frac{\pi }{3} + \frac{{k2\pi }}{3}\]
B. \[x = \pm \frac{\pi }{3} + \frac{{k2\pi }}{3}\]
C. \[x = \frac{\pi }{2} + k\pi ,x = - \frac{\pi }{3} + \frac{{k2\pi }}{3}\]
D. \[x = 2k\pi ,x = \frac{\pi }{2} + \frac{{k\pi }}{3}\]Trả lời:
\[\sin 3x - \sin x + \sin 2x = 0\]
\[ \Leftrightarrow 2cos2xsinx + 2sinxcosx = 0\]
\[ \Leftrightarrow 2sinx(cos2x + cosx) = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{sinx = 0}\\{cos2x = - cosx = cos(\pi - x)}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{\begin{array}{*{20}{c}}{2x = \pi - x + k2\pi }\\{2x = x - \pi + k2\pi }\end{array}}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{x = \frac{\pi }{3} + \frac{{k2\pi }}{3}}\\{x = - \pi + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{x = \frac{\pi }{3} + \frac{{k2\pi }}{3}}\end{array}} \right.(k \in \mathbb{Z})\)
Vậy nghiệm của phương trình là:\[x = k\pi ,x = \frac{\pi }{3} + \frac{{k2\pi }}{3}\]
Đáp án cần chọn là: A
