Các bài toán về mối quan hệ giữa hai đường thẳng
-
936 lượt thi
-
21 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho \[d,d'\] là các đường thẳng có VTCP lần lượt là \[\overrightarrow u ,\overrightarrow {u\prime } ,M \in d,M\prime \in d\prime \]Khi đó \[d \equiv d\prime \;\] nếu:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 1 - 3t}\\{y = - t}\\{z = 1 - 2t}\end{array}} \right.\) và \[{d_2}:\frac{{x - 1}}{{ - 3}} = \frac{{y - 2}}{1} = \frac{{z - 3}}{2}\].
Vị trí tương đối của d1 và d2 là:
 Xem đáp án
Xem đáp án
Đường thẳng\[{d_1}\] đi qua\[{M_1}\left( { - 1;0;1} \right)\] và có VTCP\[\overrightarrow {{u_1}} = \left( {3; - 1; - 2} \right)\]
Đường thẳng\[{d_2}\] đi qua \[{M_2}\left( {1;2;3} \right)\] và có VTCP\[\overrightarrow {{u_2}} = \left( { - 3;1;2} \right)\]
Ta có\[\frac{3}{{ - 3}} = \frac{{ - 1}}{1} = \frac{{ - 2}}{2}\] nên\[\overrightarrow {{u_1}} \parallel \overrightarrow {{u_2}} \](1)
\[\frac{{ - 1 - 1}}{{ - 3}} \ne \frac{{0 - 2}}{1} \ne \frac{{1 - 3}}{2}\] nên\[{M_1} \notin {d_2}\](2)
Từ (1) và (2), suy ra d1 và d2 song song.
Đáp án cần chọn là: A
Câu 3:
Điều kiện cần và đủ để hai đường thẳng cắt nhau là:
 Xem đáp án
Xem đáp án
d cắt\[d' \Leftrightarrow \vec u,\overrightarrow {u'} \] không cùng phương và\[\vec u,\overrightarrow {u'} ,\overrightarrow {MM'} \] đồng phẳng
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left[ {\vec u,\overrightarrow {u'} } \right] \ne \vec 0}\\{\left[ {\vec u,\overrightarrow {u'} } \right]\overrightarrow {MM'} = 0}\end{array}} \right.\)
Đáp án cần chọn là: A
Câu 4:
Cho d,d′ là các đường thẳng có VTCP lần lượt là \[\overrightarrow u ,\overrightarrow u \prime ,M \in d,M\prime \in d\prime .\]Nếu \[\left[ {\vec u,\overrightarrow {u'} } \right]\overrightarrow {MM'} \ne 0\]thì:
 Xem đáp án
Xem đáp án
Ta có: d chéo\[d' \Leftrightarrow \vec u,\overrightarrow {u'} ,\overrightarrow {MM'} \] không đồng phẳng \[ \Leftrightarrow \left[ {\vec u,\overrightarrow {u'} } \right]\overrightarrow {MM'} \ne 0\]
Đáp án cần chọn là: D
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
\[{d_1}:\frac{{x - 3}}{1} = \frac{{y - 2}}{2} = \frac{{z - 1}}{1}\;\]và \({d_2}:\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = 2}\\{z = 2 + t}\end{array}} \right.\) Vị trí tương đối của d1 và d2 là:
 Xem đáp án
Xem đáp án
Đường thẳng d1 đi qua \[{M_1}\left( {3;2;1} \right)\] và có VTCP\[\overrightarrow {{u_1}} = \left( {1;2;1} \right)\]
Đường thẳng d2 đi qua\[{M_2}\left( {0;2;2} \right)\] và có VTCP\[\overrightarrow {{u_2}} = \left( {1;0;1} \right)\]
Ta có\[\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {2;0; - 2} \right),\overrightarrow {{M_1}{M_2}} = \left( { - 3;0;1} \right)\]
Suy ra\[\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} = - 6 + 0 - 2 = - 8 \ne 0\]
Do đó d1 và d2 chéo nhau.
Đáp án cần chọn là: D
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = - 1 + 2t}\\{y = - t}\\{z = - 2 - t}\end{array}} \right.\). Trong các đường thẳng sau, đường thẳng nào vuông góc với d?
 Xem đáp án
Xem đáp án
Đường thẳng d1 có VTCP\[{\vec u_{_1}} = \left( {3;1;5} \right)\] đường thẳng d có VTCP\[{\vec u_{_d}} = \left( {2; - 1; - 1} \right)\]
Vì\[{\vec u_{_d}}.{\vec u_{_1}} = 3.2 - 1.1 - 5.1 = 0\]
Đáp án cần chọn là: A
Câu 7:
Công thức tính khoảng cách từ điểm A đến đường thẳng d′ đi qua điểm M′ và có VTCP \(\overrightarrow {u'} \)là:
 Xem đáp án
Xem đáp án
Khoảng cách từ điểm A đến đường thẳng d′ được tính theo công thức
\[d\left( {A,d'} \right) = \frac{{\left| {\left[ {\overrightarrow {AM'} ,\overrightarrow {u'} } \right]} \right|}}{{\left| {\overrightarrow {u'} } \right|}}\]
Đáp án cần chọn là: A
Câu 8:
Khoảng cách từ điểm M(2;0;1) đến đường thẳng \[\Delta :\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z - 2}}{1}\;\] là:
 Xem đáp án
Xem đáp án
Đường thẳng \[{\rm{\Delta }}\] đi qua A(1;0;2) và có VTCP\[\vec u = \left( {1;2;1} \right)\] Khi đó:
\[\overrightarrow {MA} = \left( { - 1;0;1} \right),\vec u = \left( {1;2;1} \right)\]
\[ \Rightarrow \left[ {\overrightarrow {MA} ,\vec u} \right] = \left( {\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}0\\2\end{array}}&{\begin{array}{*{20}{l}}1\\1\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}1\\1\end{array}}&{\begin{array}{*{20}{l}}{ - 1}\\1\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{ - 1}\\1\end{array}}&{\begin{array}{*{20}{l}}0\\2\end{array}}\end{array}} \right|} \right) = \left( { - 2;2; - 2} \right)\]
Vậy\[d\left( {M,{\rm{\Delta }}} \right) = \frac{{\left| {\left[ {\overrightarrow {MA} ,\vec u} \right]} \right|}}{{\left| {\vec u} \right|}} = \frac{{\sqrt {{2^2} + {2^2} + {2^2}} }}{{\sqrt {{1^2} + {2^2} + {1^2}} }} = \sqrt 2 \]
Đáp án cần chọn là: A
Câu 9:
Cho hai điểm A(1;−2;0),B(0;1;1), độ dài đường cao OH của tam giác OAB là:
 Xem đáp án
Xem đáp án
Ta có:\[\overrightarrow {OA} = \left( {1; - 2;0} \right),\overrightarrow {AB} = \left( { - 1;3;1} \right)\]
\[ \Rightarrow \left[ {\overrightarrow {OA} ,\overrightarrow {AB} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{ - 2}\\3\end{array}}&{\begin{array}{*{20}{l}}0\\1\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}0\\1\end{array}}&{\begin{array}{*{20}{l}}1\\{ - 1}\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}1\\{ - 1}\end{array}}&{\begin{array}{*{20}{l}}{ - 2}\\3\end{array}}\end{array}} \right|} \right) = \left( { - 2; - 1;1} \right)\]
Do đó\[OH = d\left( {O,AB} \right) = \frac{{\left| {\left[ {\overrightarrow {OA} ,\overrightarrow {AB} } \right]} \right|}}{{\left| {\overrightarrow {AB} } \right|}} = \frac{{\sqrt {{2^2} + {1^2} + {1^2}} }}{{\sqrt {{1^2} + {3^2} + {1^2}} }} = \frac{{\sqrt {66} }}{{11}}\]
Đáp án cần chọn là: D
Câu 10:
Cho hai đường thẳng \[\Delta ,\Delta \prime \;\] có VTCP lần lượt là \(\overrightarrow u ,\overrightarrow {u'} \) và đi qua các điểm M,M′. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 11:
Khoảng cách giữa hai đường thẳng \({d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 2 + 2t}\\{y = - 1 + t}\\{z = 1}\end{array}} \right.,{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 1 + t}\\{z = 3 - t}\end{array}} \right.\) là:
 Xem đáp án
Xem đáp án
Đường thẳng d1 đi qua\[{M_1}\left( {2; - 1;1} \right)\] và có VTCP\[\overrightarrow {{u_1}} = \left( {2;1;0} \right)\]
Đường thẳng d2 đi qua\[{M_2}\left( {1;1;3} \right)\] và có VTCP\[\overrightarrow {{u_2}} = \left( {0;1; - 1} \right)\]
Suy ra
\[\overrightarrow {{M_1}{M_2}} = \left( { - 1;2;2} \right);\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}1\\1\end{array}}&{\begin{array}{*{20}{l}}0\\{ - 1}\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}0\\{ - 1}\end{array}}&{\begin{array}{*{20}{l}}2\\0\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}2\\0\end{array}}&{\begin{array}{*{20}{l}}1\\1\end{array}}\end{array}} \right|} \right) = \left( { - 1;2;2} \right)\]
Vậy
\[d\left( {{d_1},{d_2}} \right) = \frac{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}} = \frac{{\left| {\left( { - 1} \right).\left( { - 1} \right) + 2.2 + 2.2} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = 3\]
Đáp án cần chọn là: B
Câu 12:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
\[{d_1}:\frac{{x - 2}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{1},{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = 1 + 2t}\\{z = - 1 + t}\end{array}} \right.\] và điểm A(1;2;3).
Đường thẳng Δ qua A, vuông góc với d1 và cắt d2 có phương trình là:
 Xem đáp án
Xem đáp án
Đường thẳng d1 có vectơ chỉ phương\[\overrightarrow {{u_1}} = \left( {2; - 1;1} \right)\]
Gọi\[B = {\rm{\Delta }} \cap {d_2}\] suy ra\[B \in {d_2}\] nên\[B\left( {1 - t;1 + 2t; - 1 + t} \right)\]
Đường thẳng \[{\rm{\Delta }}\] có vectơ chỉ phương\[\overrightarrow {AB} = \left( { - t;2t - 1;t - 4} \right)\]
Theo giả thiết, ta có \[{\rm{\Delta }} \bot {d_1}\] nên
\[\overrightarrow {AB} .\overrightarrow {{u_1}} = 0 \Leftrightarrow 2\left( { - t} \right) - 1\left( {2t - 1} \right) + \left( {t - 4} \right) = 0 \Leftrightarrow t = - 1 \Rightarrow B\left( {2; - 1; - 2} \right)\]
Khi đó \[{\rm{\Delta }}\] đi qua hai điểm A(1;2;3) và B(2;−1;−2) nên
Đáp án cần chọn là: A
Câu 13:
Góc giữa hai đường thẳng có các VTCP lần lượt là \(\overrightarrow u ,\overrightarrow {u'} \) thỏa mãn:
 Xem đáp án
Xem đáp án
Góc giữa hai đường thẳng có các VTCP lần lượt là\[\vec u,\overrightarrow {u'} \]
\[\cos \varphi = \left| {\cos \left( {\vec u,\overrightarrow {u'} } \right)} \right| = \frac{{\left| {\vec u.\overrightarrow {u'} } \right|}}{{\left| {\vec u} \right|.\left| {\overrightarrow {u'} } \right|}}\]
Đáp án cần chọn là: A
Câu 14:
Cho hình lập phương A(0;0;0),B(1;0;0),D(0;1;0),A′(0;0;1). Gọi M,N lần lượt là trung điểm của AB,CD. Khoảng cách giữa MN và A′C là:
 Xem đáp án
Xem đáp án
Gọi C(x;y;z) ta có
\(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 - 0 = x - 0}\\{0 - 0 = y - 1}\\{0 - 0 = z - 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 1}\\{z = 0}\end{array}} \right. \Rightarrow C(1;1;0)\)
Lại có
\[\begin{array}{*{20}{l}}{M\left( {\frac{1}{2};0;0} \right),N\left( {\frac{1}{2};1;0} \right) \Rightarrow \overrightarrow {MN} = \left( {0;1;0} \right),\overrightarrow {A'C} = \left( {1;1; - 1} \right),\overrightarrow {MA'} = \left( { - \frac{1}{2};0;1} \right)}\\{ \Rightarrow \left[ {\overrightarrow {MN} ,\overrightarrow {A'C} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}1\\1\end{array}}&{\begin{array}{*{20}{l}}0\\{ - 1}\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}0\\{ - 1}\end{array}}&{\begin{array}{*{20}{l}}0\\1\end{array}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}0\\1\end{array}}&{\begin{array}{*{20}{l}}1\\1\end{array}}\end{array}} \right|} \right) = \left( { - 1;0; - 1} \right)}\end{array}\]
Vậy
\[d\left( {MN,A'C} \right) = \frac{{\left| {\left[ {\overrightarrow {MN} ,\overrightarrow {A'C} } \right].\overrightarrow {MA'} } \right|}}{{\left| {\left[ {\overrightarrow {MN} ,\overrightarrow {A'C} } \right]} \right|}} = \frac{{\left| {\left( { - 1} \right).\left( { - \frac{1}{2}} \right) + 0.0 + \left( { - 1} \right).1} \right|}}{{\sqrt {{{\left( { - 1} \right)}^2} + {0^2} + {{\left( { - 1} \right)}^2}} }} = \frac{1}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\]
Đáp án cần chọn là: B
Câu 15:
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(0;0;2), B(1;0;0), C(2;2;0) và D(0;m;0). Điều kiện cần và đủ của m để khoảng cách giữa hai đường thẳng AB và CD bằng 2 là:
 Xem đáp án
Xem đáp án
Ta có\[\overrightarrow {AB} = \left( {1;0; - 2} \right),\overrightarrow {CD} = \left( { - 2;m - 2;0} \right)\] và\[\overrightarrow {AC} = \left( {2;2; - 2} \right)\]
Suy ra\[\left[ {\overrightarrow {AB} ;\overrightarrow {CD} } \right] = \left( {2m - 4;4;m - 2} \right)\]
Do đó
\[d\left[ {AB,CD} \right] = \frac{{\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {CD} } \right].\overrightarrow {AC} } \right|}}{{\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {CD} } \right]} \right|}} \Leftrightarrow \frac{{\left| {2\left( {2m - 4} \right) + 8 - 2\left( {m - 2} \right)} \right|}}{{\sqrt {{{\left( {2m - 4} \right)}^2} + {4^2} + {{\left( {m - 2} \right)}^2}} }} = 2\]
\[ \Leftrightarrow |2m + 4| = 2\sqrt {5{m^2} - 20m + 36} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 4}\\{m = 2}\end{array}} \right.\]
Đáp án cần chọn là: C
Câu 16:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình \[\frac{{x - 1}}{3} = \frac{{y + 2}}{2} = \frac{{z - 3}}{{ - 4}}\;\] và \[d\prime :\frac{{x + 1}}{4} = \frac{y}{1} = \frac{{z + 1}}{2}\;\;\]. Điểm nào sau đây không thuộc đường thẳng d nhưng thuộc đường thẳng d′?
 Xem đáp án
Xem đáp án
A:\[\frac{{4 - 1}}{3} = \frac{{0 + 2}}{2} = \frac{{ - 1 - 3}}{{ - 4}} = 1 \Rightarrow N \in d\]
B:\[\frac{{1 - 1}}{3} = \frac{{ - 2 + 2}}{2} = \frac{{3 - 3}}{{ - 4}} = 0 \Rightarrow M \in d\]
C:\[\frac{{7 - 1}}{3} = \frac{{2 + 2}}{2} \ne \frac{{1 - 3}}{{ - 4}} \Rightarrow P \notin d\] và\[\frac{{7 + 1}}{4} = \frac{2}{1} \ne \frac{{1 + 1}}{2} \Rightarrow P \notin d'\]
D:\[\frac{{7 - 1}}{3} = \frac{{2 + 2}}{2} \ne \frac{{3 - 3}}{{ - 4}} \Rightarrow Q \notin d\] và \[\frac{{7 + 1}}{4} = \frac{2}{1} = \frac{{3 + 1}}{2} \Rightarrow Q \in d'\]
Đáp án cần chọn là: D
Câu 17:
Trong không gian Oxyz, cho đường thẳng \({d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 + t}\\{z = 3}\end{array}} \right.\)và \({d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 2 + 7t}\\{z = 3 + t}\end{array}} \right.\). Phương trình đường phân giác của góc nhọn giữa d1 và d2 là:
 Xem đáp án
Xem đáp án
\({d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 + t}\\{z = 3}\end{array}} \right.\) có 1 VTCP là\[\overrightarrow {{u_1}} = \left( {1;1;0} \right),\,\,\left| {\overrightarrow {{u_1}} } \right| = \sqrt 2 \]
\({d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 2 + 7t}\\{z = 3 + t}\end{array}} \right.\) có 1 VTCP là\[\overrightarrow {{u_2}} = \left( {0;7;1} \right),\,\,\left| {\overrightarrow {{u_2}} } \right| = 5\sqrt 2 \]
Ta có: \[\overrightarrow {{u_1}} .\overrightarrow {{u_2}} = 0 + 7 + 0 > 0 \Rightarrow \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right) < {90^0}\]
⇒Đường phân giác góc nhọn giữa d1 và d2 có 1 VTCP\[\vec u = 5.\overrightarrow {{u_1}} + \overrightarrow {{u_2}} = \left( {5;12;1} \right)\]
Phương trình đường phân giác của góc nhọn giữa d1 và d2 là:
\[\frac{{x - 1}}{5} = \frac{{y - 2}}{{12}} = \frac{{z - 3}}{1}\]
Đáp án cần chọn là: D
Câu 18:
Trong không gian Oxyz, cho hai điểm M(−2;−2;1),A(1;2;−3) và đường thẳng \[d:\frac{{x + 1}}{2} = \frac{{y - 5}}{2} = \frac{z}{{ - 1}}.\] Gọi \[\Delta \] là đường thẳng qua M, vuông góc với đường thẳng d, đồng thời cách điểm A một khoảng bé nhất. Khoảng cách bé nhất đó là
 Xem đáp án
Xem đáp án
Gọi (P) là mặt phẳng qua M(−2;−2;1) và nhận\[\overrightarrow {{u_d}} = \left( {2;2; - 1} \right)\] làm VTPT
Phương trình mặt phẳng\[\left( P \right):2\left( {x + 2} \right) + 2\left( {y + 2} \right) - \left( {z - 1} \right) = 0\]
\[ \Leftrightarrow 2x + 2y - z + 9 = 0\]
Suy ra\[{\rm{\Delta }} \subset \left( P \right)\]. Khi đó ta có \[d\left( {A,{\rm{\Delta }}} \right) \ge d\left( {A,\left( P \right)} \right)\]
Lại có\[d\left( {A,\left( P \right)} \right) = \frac{{\left| {2.1 + 2.2 - \left( { - 3} \right) + 9} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 6\]
Vậy khoảng cách nhỏ nhất là d=6.
Đáp án cần chọn là: B
Câu 19:
Trong không gian Oxyz , cho đường thẳng \[d:\,\,\frac{{x - 3}}{2} = \frac{{y - 4}}{1} = \frac{{z - 2}}{1}\] và 2 điểm A(6;3;−2); B(1;0;−1). Gọi \[\Delta \] là đường thẳng đi qua B, vuông góc với d và thỏa mãn khoảng cách từ A đến \[\Delta \] là nhỏ nhất. Một vectơ chỉ phương của \[\Delta \] có tọa độ :
 Xem đáp án
Xem đáp án
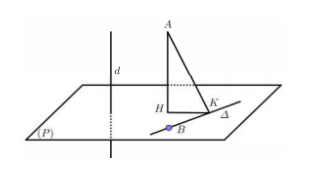
Gọi (P) là mặt phẳng đi qua B và vuông góc với\[d \Rightarrow \left( P \right):\,\,2x + y + z - 1 = 0\]
\[{\rm{\Delta }}\] đi qua B và vuông góc với\[d \Rightarrow {\rm{\Delta }} \subset \left( P \right)\]
Gọi H,K lần lượt là hình chiếu của A lên (P) và \[{\rm{\Delta }}\] ta có \[AH \le AK\]
Do đó để khoảng cách từ A đến \[{\rm{\Delta }}\] là nhỏ nhất\[ \Rightarrow H \in {\rm{\Delta }}\]
Phương trình AH đi qua A và nhận\[\overrightarrow {{u_d}} = \left( {2;1;1} \right)\] là 1 VTCP là\(\left\{ {\begin{array}{*{20}{c}}{x = 6 + 2t}\\{y = 3 + t}\\{z = - 2 + t}\end{array}} \right.\)\[\begin{array}{*{20}{l}}{H \in AH \Rightarrow H\left( {6 + 2t;3 + t; - 2 + t} \right)}\\{H \in \left( P \right) \Rightarrow 2\left( {6 + 2t} \right) + 3 + t - 2 + t - 1 = 0 \Leftrightarrow 6t + 12 = 0 \Leftrightarrow t = - 2}\\{ \Rightarrow H\left( {2;1; - 4} \right)}\end{array}\]
\[{\rm{\Delta }}\] đi qua B,H nhận\[\overrightarrow {BH} \left( {1;1; - 3} \right)\] là 1 VTCP.
Đáp án cần chọn là: A
Câu 20:
Trong không gian Oxyz cho điểm A(1;1;−2) và đường thẳng \[d:\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{z}{{ - 2}}\]. Đường thẳng qua A và song song với d có phương trình tham số là
 Xem đáp án
Xem đáp án
Đường thẳng\[d:\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{z}{{ - 2}}\] có 1 VTCP là \[\overrightarrow {{u_d}} = \left( {2;1; - 2} \right)\] đây cũng là VTCP của đường thẳng đi qua A và song song với d.
Đường thẳng qua A và song song với d nhận\[\vec u = \left( {2;1; - 2} \right)\] là VTCP, có phương trình tham số: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = 1 + t}\\{z = - 2 - 2t}\end{array}} \right.\)
Đáp án cần chọn là: B
Câu 21:
Trong không gian Oxyz, cho đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 - t}\\{z = 1 - 3t}\end{array}} \right.\). Đường thẳng \[\Delta \] đi qua gốc tọa độ O, vuông góc với trục hoành Ox và vuông góc với đường thẳng d có phương trình là:
 Xem đáp án
Xem đáp án
Đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 - t}\\{z = 1 - 3t}\end{array}} \right.\) có 1 VTCP là\[\overrightarrow {{u_d}} = \left( {1; - 1; - 3} \right)\] trục Ox có 1 VTCP là\[\vec i = \left( {1;0;0} \right)\]
Gọi\[\overrightarrow {{u_{\rm{\Delta }}}} \] là 1 VTCP của đường thẳng \[{\rm{\Delta }}\], ta có
\(\left\{ {\begin{array}{*{20}{c}}{\Delta \bot Ox}\\{\Delta \bot d}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\overrightarrow {{u_\Delta }} .\overrightarrow i = 0}\\{\overrightarrow {{u_\Delta }} .\overrightarrow {{u_d}} = 0}\end{array}} \right. \Rightarrow \overrightarrow {{u_\Delta }} = \left[ {\overrightarrow i ;\overrightarrow {{u_d}} } \right] = (0; - 3;1)\)
Vậy phương trình đường thẳng \[{\rm{\Delta }}\] đi qua O(0;0;0) và có 1 VTCP\[\overrightarrow {{u_{\rm{\Delta }}}} = \left( {0; - 3;1} \right)\] là:
\(\Delta :\left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = - 3t}\\{z = t}\end{array}} \right.\)
Đáp án cần chọn là: D
