Khoảng cách giữa hai đường thẳng chéo nhau
-
1439 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
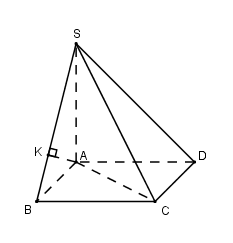
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với \(AC = \frac{{a\sqrt 2 }}{2}\). Cạnh bên SA vuông góc với đáy, SB hợp với đáy góc 600. Tính khoảng cách d giữa hai đường thẳng AD và SC.
 Xem đáp án
Xem đáp án
Ta có
\[SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}\]
Tam giác ABC vuông cân tại B nên\[AB = BC = \frac{{AC}}{{\sqrt 2 }} = \frac{a}{2}\]
Xét tam giác vuông SAB có\[SA = AB.\tan {60^0} = \frac{a}{2}.\sqrt 3 = \frac{{a\sqrt 3 }}{2}\]
Ta có\[d\left( {AD;SC} \right) = d\left( {AD;\left( {SBC} \right)} \right) = d\left( {A;\left( {SBC} \right)} \right)\]
Kẻ \[AK \bot SB\]
Do\(\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AK\) mà\[AK \bot SB\] nên\[AK \bot \left( {SBC} \right)\]
Khi đó\[d\left( {A;\left( {SBC} \right)} \right) = AK = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{a}{2}}}{{\sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2}} }} = \frac{{a\sqrt 3 }}{4}\]
Đáp án cần chọn là: A
Câu 2:
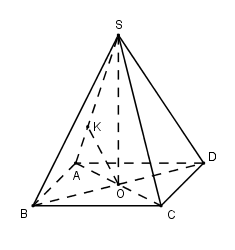
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 2. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \sqrt 3 \). Tính khoảng cách d giữa hai đường thẳng SA và BD.
 Xem đáp án
Xem đáp án
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BD \bot AC}\\{BD \bot SO}\end{array}} \right. \Rightarrow BD \bot (SAC)\)
Trong (SAC) kẻ\[OK \bot SA\,\,\left( 1 \right)\] ta có\[OK \subset \left( {SAC} \right) \Rightarrow OK \bot BD\,\,\,\left( 2 \right)\]
Từ (1) và (2) ta có OK là đường vuông góc chung của SA và BD. Khi đó
\[d\left( {SA;BD} \right) = OK = \frac{{SO.OA}}{{\sqrt {S{O^2} + O{A^2}} }} = \frac{{\sqrt 3 .\frac{{2\sqrt 2 }}{2}}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\frac{{2\sqrt 2 }}{2}} \right)}^2}} }} = \frac{{\sqrt {30} }}{5}.\]
Đáp án cần chọn là: B
Câu 3:
Cho hình lăng trụ ABC.A′B′C′ có đáy là tam giác đều cạnh có độ dài bằng 2a. Hình chiếu vuông góc của A′A′ lên mặt phẳng (ABC) trùng với trung điểm H của BC. Tính khoảng cách d giữa hai đường thẳng BB′ và A′H.
 Xem đáp án
Xem đáp án
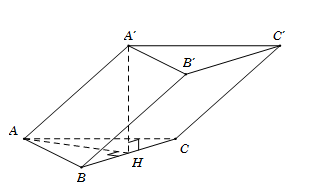
Do\[BB'\parallel AA'\] nên\[d\left( {BB';A'H} \right) = d\left( {BB';\left( {AA'H} \right)} \right) = d\left( {B;\left( {AA'H} \right)} \right).\]
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BH \bot AH}\\{BH \bot A\prime H}\end{array}} \right. \Rightarrow BH \bot (AA\prime H)\)
Nên\[d\left( {B;\left( {AA'H} \right)} \right) = BH = \frac{{BC}}{2} = a.\]
Vậy khoảng cách\[d\left( {BB';A'H} \right) = a\]
Đáp án cần chọn là: B
Câu 4:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, tam giác SBC là tam giác đều cạnh aa và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng SA và BC.
 Xem đáp án
Xem đáp án
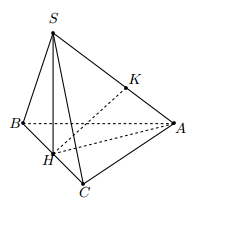
Gọi H là trung điểm của BC khi đó\[SH \bot BC\]
Mặt khác \[\left( {SBC} \right) \bot \left( {ABC} \right)\] do đó\[SH \bot \left( {ABC} \right)\]
Ta có\[SH = \frac{{a\sqrt 3 }}{2}\] và\[AB = AC = \frac{a}{{\sqrt 2 }};AH = \frac{{BC}}{2} = \frac{a}{2}\]
Do\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AH}\\{BC \bot SH}\end{array}} \right. \Rightarrow BC \bot (SHA)\)
Dựng\[HK \bot SA\] khi đó HK là đoạn vuông góc chung của BC và SA.
Lại có \[HK = \frac{{SH.AH}}{{\sqrt {S{H^2} + H{A^2}} }} = \frac{{a\sqrt 3 }}{4}\] Vậy \[d\left( {SA;BC} \right) = \frac{{a\sqrt 3 }}{4}.\]
Đáp án cần chọn là: B
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết mặt phẳng (SBC) tạo với đáy một góc 600 và M là trung điểm của SD. Tính khoảng cách d giữa hai đường thẳng AB và CM.
 Xem đáp án
Xem đáp án
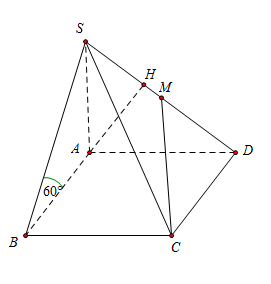
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot (SAB)\)
\[ \Rightarrow \widehat {SBA}\] là góc giữa 2 mặt phẳng (SBC) và (ABC)
Ta có \[SA = AB\tan \widehat {SBA} = a\sqrt 3 \]
Do AB||CD do đó\[d\left( {AB;CM} \right) = d\left( {AB;\left( {CMD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\]
Dựng\[AH \bot SD\,\,\,\left( 1 \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{CD \bot AD}\\{CD \bot SA}\end{array}} \right. \Rightarrow CD \bot (SAD) \Rightarrow CD \bot AH(2)\)
Từ (1) và (2)\[ \Rightarrow AH \bot \left( {SCD} \right)\]
khi đó\[d\left( {A;\left( {SCD} \right)} \right) = AH\]
Lại có\[AH = \frac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \frac{{a\sqrt 3 }}{2}.\]
Do đó\[d = \frac{{a\sqrt 3 }}{2}.\]
Đáp án cần chọn là: B
Câu 6:
Cho hình chóp S.ABC có đáy ABCD là hình vuông cạnh a, tâm O. Cạnh bên SA=2a và vuông góc với mặt đáy (ABCD). Gọi H và K lần lượt là trung điểm của cạnh BC và CD. Tính khoảng cách giữa hai đường thẳng HK và SD.
 Xem đáp án
Xem đáp án
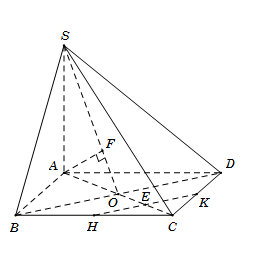
Gọi\[E = HK \cap AC.\] Do \[HK\parallel BD\] nên suy ra\[d\left( {HK;SD} \right) = d\left( {HK;\left( {SBD} \right)} \right) = d\left( {E;\left( {SBD} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SBD} \right)} \right)\]
(vì \[OE = \frac{1}{2}AO\])
Kẻ \[AF \bot SO\,\,\left( 1 \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{BD \bot AC}\\{BD \bot SA}\end{array}} \right. \Rightarrow BD \bot (SAC) \Rightarrow BD \bot AF(2)\)
Từ (1) và (2) \[ \Rightarrow AF \bot \left( {SBD} \right)\] khi đó\[d\left( {A;\left( {SBD} \right)} \right) = AF = \frac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \frac{{2a.\frac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \frac{{{a^2}}}{2}} }} = \frac{{2a}}{3}.\]
Vậy khoảng cách\[d\left( {HK;SD} \right) = \frac{1}{2}AF = \frac{a}{3}.\]
Đáp án cần chọn là: A
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng 4a. Cạnh bên SA=2a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) là trung điểm của H của đoạn thẳng AO. Tính khoảng cách d giữa các đường thẳng SD và AB.
 Xem đáp án
Xem đáp án
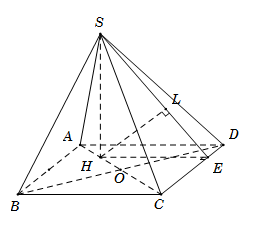
Do \[AB\parallel CD\] nên\[d\left( {SD;AB} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right) = \frac{4}{3}d\left( {H;\left( {SCD} \right)} \right).\]
(Do\[AH \cap \left( {SCD} \right) = C \Rightarrow \frac{{d\left( {A;\left( {SCD} \right)} \right)}}{{d\left( {H;\left( {SCD} \right)} \right)}} = \frac{{AC}}{{HC}} = \frac{4}{3}\]
\[ \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = \frac{4}{3}d\left( {H;\left( {SCD} \right)} \right)\]
Kẻ\[HE \bot CD\], kẻ\[HL \bot SE\,\,\left( 1 \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{CD \bot SH}\\{CD \bot HE}\end{array}} \right. \Rightarrow CD \bot (SHE) \Rightarrow CD \bot HL(2)\)
Từ (1) và (2) \[ \Rightarrow HL \bot \left( {SCD} \right)\]
\[ \Rightarrow d\left( {H;\left( {SCD} \right)} \right) = HL\]
Tính được\[SH = \sqrt {S{A^2} - A{H^2}} = a\sqrt 2 ,HE = \frac{3}{4}AD = 3a.\]
Khi đó\[d\left( {H;\left( {SCD} \right)} \right) = HL = \frac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \frac{{3a\sqrt 2 }}{{\sqrt {11} }}.\]
Vậy\[d\left( {SD;AB} \right) = \frac{4}{3}HL = \frac{{4a\sqrt {22} }}{{11}}.\]
Đáp án cần chọn là: A
Câu 8:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, gọi I là trung điểm của AB. Hình chiếu vuông góc của S trên mặt đáy là trung điểm của CI. Biết chiều cao của khối chóp là \(a\sqrt 3 \). Khoảng cách giữa hai đường thẳng AB và SC là :
 Xem đáp án
Xem đáp án
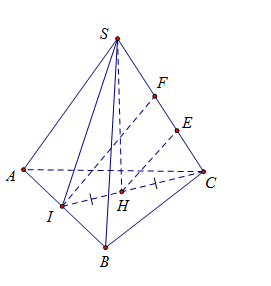
Ta có \(\left\{ {\begin{array}{*{20}{c}}{CI \bot AB}\\{SH \bot AB}\end{array}} \right. \Rightarrow AB \bot (SIC)\)
Dựng\[IF \bot SC\,\,\left( 1 \right)\] khi đó\[IF \subset \left( {SIC} \right) \Rightarrow IF \bot AB\,\,\left( 2 \right)\] do đó IF là đoạn vuông góc chung của AB và SC. Dựng \[HE \bot SC \Rightarrow HE//IF\] ta có\[HE = \frac{1}{2}IF\]
Lại có\[CI = \frac{{a\sqrt 3 }}{2} \Rightarrow CH = \frac{{a\sqrt 3 }}{4}\]
Khi đó\[HE = \frac{{SH.HC}}{{\sqrt {S{H^2} + C{H^2}} }} = \frac{{a\sqrt 3 .\frac{{a\sqrt 3 }}{4}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}} }} = \frac{{a\sqrt {51} }}{{17}} \Rightarrow IF = \frac{{2a\sqrt {51} }}{{17}}\]
Đáp án cần chọn là: C
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh aa. Cạnh bên SA vuông góc với mặt phẳng đáy. Biết góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 600. Tính khoảng cách giữa hai đường thẳng BD và SC.
 Xem đáp án
Xem đáp án
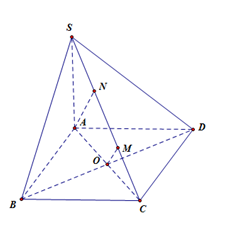
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot (SAB)\)
Khi đó\[\widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {SBA} = {60^0}\]
Suy ra\[SA = AB\tan {60^0} = a\sqrt 3 \]
Gọi O là tâm hình vuông ABCD ta có:
\(\left\{ {\begin{array}{*{20}{c}}{BD \bot AC}\\{BD \bot SA}\end{array}} \right. \Rightarrow BD \bot (SAC)\)
Trong (SAC) dựng\[OM \bot SC\,\,\left( 1 \right)\] ta có \[OM \subset \left( {SAC} \right) \Rightarrow OM \bot BD\,\,\left( 2 \right)\]T ừ (1) và (2) suy ra OM là đường vuông góc chung BD và SC.
Ta có
\[ \Rightarrow \frac{{SC}}{{CO}} = \frac{{SA}}{{MO}} \Rightarrow OM = \frac{{SA.OC}}{{SC}}\]
\[ = \frac{{a\sqrt 3 .\frac{{a\sqrt 2 }}{2}}}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{a\sqrt 6 }}{{2\sqrt 5 }} = \frac{{a\sqrt {30} }}{{10}}.\]
Đáp án cần chọn là: D
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với mặt phẳng đáy góc 450. Khoảng cách giữa hai đường thẳng SB và AC là
 Xem đáp án
Xem đáp án
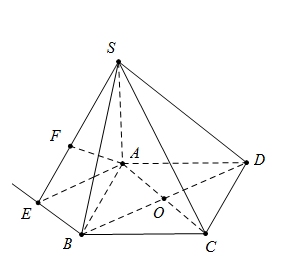
Ta có
\[AC = a\sqrt 2 ;\widehat {SCA} = \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = {45^0} \Rightarrow SA = AC = a\sqrt 2 \]
Dựng\[Bx||AC \Rightarrow d\left( {AC;SB} \right) = d\left( {AC;(SBx)} \right)\]
Dựng\[AE \bot Bx,\;AF \bot SE\,\,\,\left( 1 \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{Bx \bot AE}\\{Bx \bot SA}\end{array}} \right. \Rightarrow Bx \bot (SAE) \Rightarrow Bx \bot AF(2)\)
Từ (1) và (2) \[ \Rightarrow AF \bot \left( {SBE} \right) \Rightarrow d = d\left( {AC;\left( {SBx} \right)} \right) = d\left( {A,\left( {SBx} \right)} \right) = AF\]
Ta có\[BE||AC \Rightarrow BE \bot BD\] dễ ràng suy ra OEBO là hình chữ nhật suy ra\[AE = OB = \frac{{a\sqrt 2 }}{2}.\]
Vậy khoảng cách
\[d\left( {SB;AC} \right) = \frac{{AE.SA}}{{\sqrt {A{E^2} + S{A^2}} }} = \frac{{\frac{{a\sqrt 2 }}{2}.a\sqrt 2 }}{{\sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} }} = \frac{{a\sqrt {10} }}{5}\]
Đáp án cần chọn là: C
Câu 11:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC và đáy bằng 600. Gọi M là trung điểm của AC, tính khoảng cách dd giữa hai đường thẳng AB và SM.
 Xem đáp án
Xem đáp án
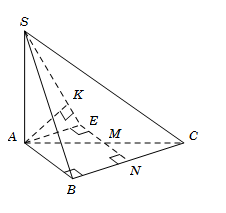
Ta có:\[AC = \sqrt {A{B^2} + B{C^2}} = 5a\]
Xác định\[{60^0} = \widehat {\left( {SC,\left( {ABC} \right)} \right)} = \widehat {\left( {SC,AC} \right)} = \widehat {SCA}\] và\[SA = AC.\tan \widehat {SCA} = 5a\sqrt 3 .\]
Gọi N là trung điểm BC, suy ra\[MN\parallel AB\]
Lấy điểm E đối xứng với N qua M, suy ra ABNE là hình chữ nhật.
Do đó\[d\left( {AB;SM} \right) = d\left( {AB;\left( {SME} \right)} \right) = d\left( {A;\left( {SME} \right)} \right).\]
Kẻ\[AK \bot SE\]
Vì\[ME \bot AE,ME \bot SA\] nên\[ME \bot \left( {SAE} \right) \Rightarrow ME \bot AK\]
Mà\[AK \bot SE\] nên \[AK \bot \left( {SME} \right)\]
Khi đó\[d\left( {A;\left( {SME} \right)} \right) = AK = \frac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \frac{{10a\sqrt 3 }}{{\sqrt {79} }}.\]
Đáp án cần chọn là: D
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên SA vuông góc với đáy, góc \(\widehat {SBD} = {60^ \circ }\). Tính khoảng cách d giữa hai đường thẳng AB và SO.
 Xem đáp án
Xem đáp án
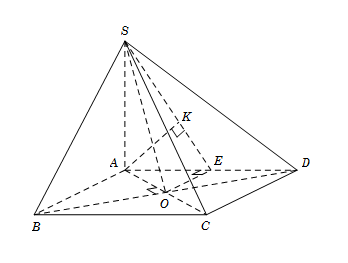
Ta có\[{\rm{\Delta }}\,SAB = {\rm{\Delta }}\,SAD\left( {c - g - c} \right)\] suy ra\[SB = SD\]
Mà\[\widehat {SBD} = {60^0} \Rightarrow {\rm{\Delta }}\,SBD\] đều cạnh\[SB = SD = BD = a\sqrt 2 \]
Tam giác vuông SAB, có\[SA = \sqrt {S{B^2} - A{B^2}} = a\]
Gọi E là trung điểm AD, suy ra\[OE\parallel AB\] và \[AE \bot OE\]
Do đó\[d\left( {AB;SO} \right) = d\left( {AB;\left( {SOE} \right)} \right) = d\left( {A;\left( {SOE} \right)} \right).\]
Kẻ\[AK \bot SE\,\,\,\left( 1 \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{OE \bot AD}\\{OE \bot SA}\end{array}} \right. \Rightarrow OE \bot (SAD) \Rightarrow OE \bot AK(2)\)
Từ (1) và (2) \[ \Rightarrow AK \bot \left( {SOE} \right)\]
\[ \Rightarrow d\left( {A;\left( {SOE} \right)} \right) = AK = \frac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }} = \frac{{a\sqrt 5 }}{5}\]
Đáp án cần chọn là: D
Câu 13:
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác vuông cân, AC=BC=3a. Hình chiếu vuông góc của B′ lên mặt đáy trùng với trọng tâm của tam giác ABC, mặt phẳng (ABB′A′) tạo với mặt phẳng (ABC) một góc 600. Tính khoảng cách giữa hai đường thẳng AB và B′C.
 Xem đáp án
Xem đáp án
Gọi G là trọng tâm tam giác ABC thì\[B'G \bot \left( {ABC} \right)\]
Dựng\[CI \bot AB\] suy ra I là trung điểm của AB.
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{AB \bot B\prime G}\\{AB \bot GI}\end{array}} \right. \Rightarrow AB \bot (B\prime GI) \Rightarrow (\widehat {(ABB\prime A\prime );(ABC)}) = \widehat {B\prime IG} = {60^0}\)
Lại có\[CI = \frac{1}{2}AB = \frac{{3a\sqrt 2 }}{2} \Rightarrow GI = \frac{1}{3}CI = \frac{{a\sqrt 2 }}{2}\]
\[ \Rightarrow B'G = GI.\tan {60^0} = \frac{{a\sqrt 6 }}{2}\]
Dựng\[IH \bot B'C\] ta có\[IH \subset \left( {B'IC} \right)\] mà \[AB \bot \left( {B'IC} \right) \Rightarrow IH \bot AB\]
\[ \Rightarrow d\left( {AB;B'C} \right) = IH = \frac{{B'G.CI}}{{B'C}}\]
Ta có :
\[B'C = \sqrt {B'{G^2} + G{C^2}} = \sqrt {\frac{{3{a^2}}}{2} + 2{a^2}} = \frac{{a\sqrt {14} }}{2} \Rightarrow IH = \frac{{3a\sqrt {42} }}{{14}}\]
Do đó\[d = IH = \frac{{3a\sqrt {42} }}{{14}}\]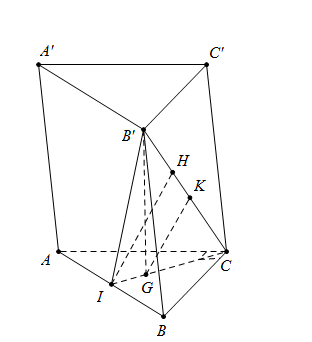
Đáp án cần chọn là: A
Câu 14:
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy ABC là tam giác vuông, \[AB = BC = a,\;A\prime B = a\sqrt 3 \]. Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AM và B′C.
 Xem đáp án
Xem đáp án
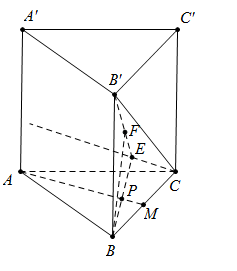
Ta có\[AA' = \sqrt {A'{B^2} - A{B^2}} = a\sqrt 2 \]
Dựng\[Cx||AM\] khi đó\[d\left( {AM;B'C} \right) = d\left( {AM;\left( {B'Cx} \right)} \right)\]
\[ = d\left( {M;\left( {B'Cx} \right)} \right) = \frac{1}{2}d\left( {B;\left( {B'Cx} \right)} \right)\]
(vì\[BM \cap \left( {B'Cx} \right) = C\] và M là trung điểm của BC)
Dựng\(\left\{ {\begin{array}{*{20}{c}}{BE \bot Cx}\\{BF \bot B\prime E(1)}\end{array}} \right.\) ta có:
\(\left\{ {\begin{array}{*{20}{c}}{Cx \bot BE}\\{Cx \bot BB\prime }\end{array}} \right. \Rightarrow Cx \bot (BB\prime E) \Rightarrow Cx \bot BF(2)\)
Từ (1) và (2)\[ \Rightarrow BF \bot \left( {B'Cx} \right) \Rightarrow d\left( {B;\left( {B'Cx} \right)} \right) = BF\]
Gọi\[P = BE \cap AM\], do \[MP//CE,MB = MC\] nên\[PB = PE\]
Mà \[BP = \frac{{AB.BM}}{{\sqrt {A{B^2} + B{M^2}} }} = \frac{{a.\frac{a}{2}}}{{\sqrt {{a^2} + \frac{{{a^2}}}{4}} }} = \frac{a}{{\sqrt 5 }}\]
Suy ra\[BE = \frac{{2a}}{{\sqrt 5 }} \Rightarrow BF = \frac{{BE.BB'}}{{\sqrt {B{E^2} + B{B^{\prime 2}}} }} = \frac{{2a}}{{\sqrt 7 }}\]
Do đó\[d = \frac{a}{{\sqrt 7 }}\]
Đáp án cần chọn là: D
Câu 15:
Cho hình lăng trụ đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là :
 Xem đáp án
Xem đáp án
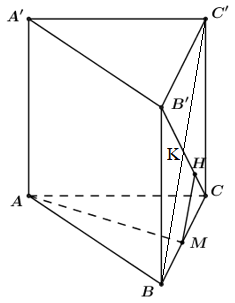
Ta có :\(\left\{ {\begin{array}{*{20}{c}}{AM \bot BC}\\{AM \bot BB\prime }\end{array}} \right. \Rightarrow AM \bot (BCC\prime B\prime )\)
Trong \[\left( {BCC'B'} \right)\] kẻ\[MH//BC'\,\,\left( {H \in B'C} \right) \Rightarrow MH \bot B'C\]
\[MH \subset \left( {BCC'B'} \right) \Rightarrow AM \bot MH\]
\[ \Rightarrow MH\] là đoạn vuông góc chung giữa AM và B’C\[ \Rightarrow d\left( {AM;B'C} \right) = MH\]
Dễ thấy\[MH = \frac{1}{2}BK = \frac{1}{4}B'C = \frac{{a\sqrt 2 }}{4}\] với K là trung điểm của B′C.\[ \Rightarrow d\left( {AM;B'C} \right) = \frac{{a\sqrt 2 }}{4}\]
Đáp án cần chọn là: B
Câu 16:
Cho tứ diện gần đều ABCD, biết \[AB = CD = 5,AC = BD = \sqrt {34} ,AD = BC = \sqrt {41} \]. Tính sin của góc giữa hai đường thẳng AB và CD.
 Xem đáp án
Xem đáp án
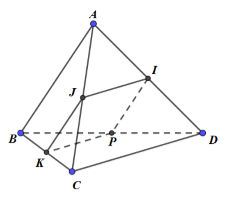
Gọi I, J, K, P lần lượt là trung điểm của AD, AC, BC, BD.
Khi đó, AB // IP // JK, CD // IJ // KP
\[ \Rightarrow \left( {\widehat {AB;CD}} \right) = \left( {\widehat {IP;KP}} \right)\]
Ta có:\[KP = \frac{1}{2}CD = \frac{5}{2},IP = \frac{1}{2}AB = \frac{5}{2}\]
\[A{K^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4} = \frac{{25 + 34}}{2} - \frac{{41}}{4} = \frac{{77}}{4} = D{K^2}\]
Tam giác AKD cân tại K, KI là trung tuyến
\[ \Rightarrow KI \bot AD \Rightarrow I{K^2} = A{K^2} - A{I^2} = \frac{{77}}{4} - \frac{{41}}{4} = 9\]
\[\cos \widehat {IPK} = \frac{{I{P^2} + K{P^2} - I{K^2}}}{{2.IP.KP}} = \frac{{\frac{{25}}{4} + \frac{{25}}{4} - 9}}{{2.\frac{5}{2}.\frac{5}{2}}} = \frac{7}{{25}} > 0 \Rightarrow \widehat {IPK} < {90^0}\]
\[ \Rightarrow \left( {\widehat {AB;CD}} \right) = \left( {\widehat {IP;KP}} \right) = \widehat {IPK} \Rightarrow \sin \left( {\widehat {AB;CD}} \right) = \sin \widehat {IPK} = \sqrt {1 - {{\left( {\frac{7}{{25}}} \right)}^2}} = \frac{{24}}{{25}}\]
Đáp án cần chọn là: A
Câu 17:
Cho tứ diện đều ABCD có cạnh bằng 2a. Khoảng cách giữa hai đường thẳng AB và CD là
 Xem đáp án
Xem đáp án
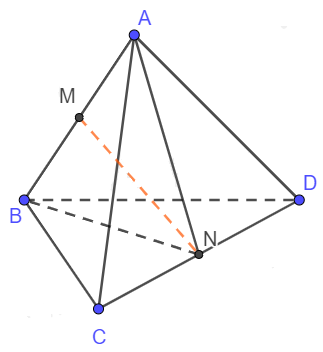
Bước 1: Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh MN là đoạn vuông góc chung của AB và CD.
Gọi M, N lần lượt là trung điểm của AB và CD.
\[{\rm{\Delta }}BCD,{\rm{\Delta }}ACD\] đều nên:
\(\left. {\begin{array}{*{20}{c}}{AN \bot CD}\\{BN \bot CD}\end{array}} \right\} \Rightarrow (ABN) \bot CD \Rightarrow MN \bot CD\)
Tương tự ta có \[MN \bot AB\]
Khoảng cách giữa 2 đường thẳng AB, CD là độ dài của MN.
Bước 2: Tính MN.
\[{\rm{\Delta }}ACD\] đều cạnh 2a; AN là đường cao.
\[ \to AN = AC.\frac{{\sqrt 3 }}{2} = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 \]
\[AM = \frac{1}{2}AB = a\]
\[{\rm{\Delta }}AMN\] vuông tại M\[MN \bot AB\] nên:
\[MN = \sqrt {A{N^2} - A{M^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \]
Đáp án cần chọn là: B
Câu 18:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AB=2a,AD=DC=a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng 600. Tính khoảng cách d giữa hai đường thẳng AC và SB.
 Xem đáp án
Xem đáp án
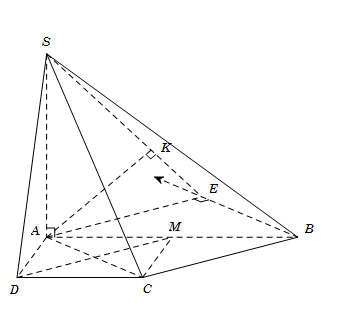
\(\left\{ {\begin{array}{*{20}{c}}{(SAB) \bot (ABCD)}\\{(SAD) \bot (ABCD)}\\{(SAB) \cap (SAD) = SA}\end{array}} \right. \Rightarrow SA \bot (ABCD)\)
Xác định
\[{60^0} = \widehat {\left( {SC;\left( {ABCD} \right)} \right)}\]
\[ = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}\]
và \[SA = AC.\tan \widehat {SCA} = \sqrt {A{D^2} + C{D^2}} .\tan {60^0} = a\sqrt 2 .\sqrt 3 = a\sqrt 6 .\]
Gọi M là trung điểm AB, suy ra ADCM là hình vuông nên CM=AD=a.
Xét tam giác ACB, ta có trung tuyến\[CM = a = \frac{1}{2}AB\] nên tam giác ACB vuông tại C.
Lấy điểm E sao cho ACBE là hình chữ nhật, suy ra \[AC\parallel BE\] và E nằm trong (ABCD).
Do đó \[d\left( {AC;SB} \right) = d\left( {AC;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right)\]
Kẻ \[AK \bot SE\,\,\,\left( 1 \right)\] ta có:\(\left\{ {\begin{array}{*{20}{c}}{BE \bot AE}\\{BE \bot SA}\end{array}} \right. \Rightarrow BE \bot (SAE) \Rightarrow BE \bot AK(2)\)
Từ (1) và (2) \[ \Rightarrow AK \bot \left( {SBE} \right)\]
Khi đó \[d\left( {A,\left( {SBE} \right)} \right) = AK = \frac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }}.\]
Ta có:\[AE = BC = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \Rightarrow AK = \frac{{a\sqrt 6 .a\sqrt 2 }}{{\sqrt {6{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{2}\]
Đáp án cần chọn là: A
Câu 19:
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh \(a\sqrt {2,} {\rm{AA}}' = 2a\). Tính khoảng cách dd giữa hai đường thẳng BD và CD′.
 Xem đáp án
Xem đáp án
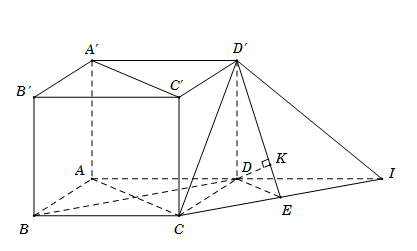
Gọi I là điểm đối xứng của A qua D,
suy ra BCID là hình bình hành nên \[BD//CI\]
Do đó\[d\left( {BD;CD'} \right) = d\left( {BD;\left( {CD'I} \right)} \right) = d\left( {D;\left( {CD'I} \right)} \right).\]
Kẻ\[DE \bot CI\] tại E, kẻ\[DK \bot D'E\,\,\left( 1 \right)\] ta có:
\(\left\{ {\begin{array}{*{20}{c}}{CI \bot DE}\\{CI \bot DD\prime }\end{array}} \right. \Rightarrow CI \bot (DD\prime E) \Rightarrow CI \bot DK(2)\)
Từ (1) và (2)\[ \Rightarrow DK \bot \left( {CD'I} \right)\]
\[ \Rightarrow d\left( {D;\left( {CD'I} \right)} \right) = DK.\]
Xét tam giác IAC, ta có DE//AC (do cùng vuông góc với CI) và có D là trung điểm của AI nên suy ra DE là đường trung bình của tam giác ACI. Suy ra\[DE = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{{\sqrt 2 }} = a.\]
Tam giác vuông D′DE, có \[DK = \frac{{D'D.DE}}{{\sqrt {D'{D^2} + D{E^2}} }} = \frac{{2a.a}}{{\sqrt {4{a^2} + {a^2}} }} = \frac{{2a\sqrt 5 }}{5}.\]
Đáp án cần chọn là: C
