Hàm số mũ
-
1420 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hàm số \[y = {a^x}(0 < a \ne 1)\] đồng biến khi nào?
 Xem đáp án
Xem đáp án
Hàm số mũ \[y = {a^x}(0 < a \ne 1)\] đồng biến khi a > 1.
Đáp án cần chọn là: A
Câu 2:
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Đồ thị hàm số \[y = {a^x}(0 < a \ne 1)\]nằm hoàn toàn phía trên trục hoành.
Đáp án cần chọn là: D
Câu 3:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Ta có:
Hàm số\[y = {a^{ - x}}\] nghịch biến khi a>1 nên các đáp án B, D đều sai.
\[y = {a^{ - x}} = \frac{1}{{{a^x}}} = {\left( {\frac{1}{a}} \right)^x}(0 < a \ne 1)\] nên hàm số đồng biến nếu\[\frac{1}{a} > 1 \Leftrightarrow 0 < a < 1\]
Đáp án cần chọn là: C
Câu 4:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Ta có: \[y = {\left( {\frac{1}{2}} \right)^{ - x}} = \frac{1}{{{{\left( {\frac{1}{2}} \right)}^x}}} = \frac{1}{{\frac{1}{{{2^x}}}}} = {2^x}\] nên hai hàm số\[y = {2^x}\] và\[y = {\left( {\frac{1}{2}} \right)^{ - x}}\] là một. Do đó chúng có chung đồ thị.
Đáp án cần chọn là: A
Câu 5:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Vì\[{\left( {\frac{1}{3}} \right)^x}\] và \[ - {\left( {\frac{1}{3}} \right)^x}\] đối nhau nên đồ thị hai hàm số đó đối xứng nhau qua Ox.
Đáp án cần chọn là: B
Câu 6:
Đồ thị sau là đồ thị hàm số nào?
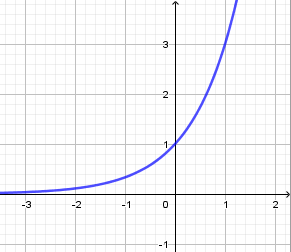
 Xem đáp án
Xem đáp án
Dáng đồ thị là của hàm số y = ax với a > 1 nên loại A và C.
Đồ thị hàm số đi qua điểm (1;3) nên chỉ có D thỏa mãn.
Đáp án cần chọn là: D
Câu 7:
Đồ thị hàm số dưới đây là của hàm số nào?
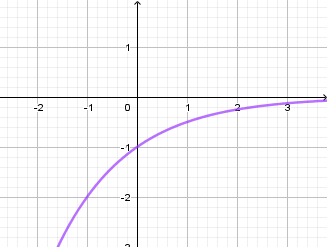
 Xem đáp án
Xem đáp án
Quan sát đồ thị ta thấy nó nằm hoàn toàn phía dưới trục hoành nên loại A và B.
Lại có, đồ thị hàm số đi qua điểm (−1;−2) nên thay tọa độ điểm này vào các hàm số C và D ta được đáp án C.
Đáp án cần chọn là: C
Câu 8:
Cho các đồ thị hàm số \[y = {a^x},y = {b^x},y = {c^x}(0 < a,b,c \ne 1)\] chọn khẳng định đúng:
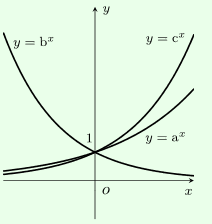
 Xem đáp án
Xem đáp án
Ta thấy:
- Hàm số \[y = {b^x}\] nghịch biến nên \[0 < b < 1\]
- Hàm số \[y = {a^x},y = {c^x}\]đồng biến nên \[a,c > 1 > b\], loại B và D.
- Xét phần đồ thị hai hàm số \[y = {a^x},y = {c^x}\] ta thấy phần đồ thị hàm số \[y = {c^x}\] nằm trên đồ thị hàm số \[y = {a^x}\] nên \[{c^x} > {a^x},\forall x > 0 \Leftrightarrow c > a\].
Đáp án cần chọn là: A
Câu 9:
Cho hai hàm số \[y = {a^x},y = {b^x}\] với \[1 \ne a,b > 0\;\]lần lượt có đồ thị là (C1),(C2) như hình bên. Mệnh đề nào đúng?
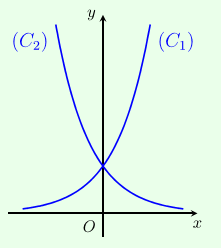
 Xem đáp án
Xem đáp án
Ta thấy: Đồ thị hàm số \[y = {b^x}\] đi xuống nên hàm số \[y = {b^x}\] nghịch biến nên 0<b<1.
Đồ thị hàm số \[y = {a^x}\] đi lên nên hàm số \[y = {a^x}\] đồng biến nên a>1.
Vậy 0<b<1<a.
Đáp án cần chọn là: B
Câu 10:
Hàm số \[y = {2^{\ln x + {x^2}}}\] có đạo hàm là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 11:
Cho hàm số \[y = {3^x} + \ln 3\]. Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Ta có:\[y = {3^x} + \ln 3 \Rightarrow y' = {3^x}\ln 3\]
Lại có:\[y = {3^x} + \ln 3 \Rightarrow {3^x} = y - \ln 3 \Rightarrow y' = \left( {y - \ln 3} \right)\ln 3 = y\ln 3 - {\ln ^2}3\]
Đáp án cần chọn là: A
Câu 12:
Cho giới hạn \[I = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{3x}} - {e^{2x}}}}{x}\], chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Ta có:\[I = \mathop {\lim }\limits_{x \to 0} \frac{{{e^{3x}} - {e^{2x}}}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {{e^{3x}} - 1} \right) - \left( {{e^{2x}} - 1} \right)}}{x}\]
\[ = \mathop {\lim }\limits_{x \to 0} \left[ {3.\frac{{{e^{3x}} - 1}}{{3x}} - 2.\frac{{{e^{2x}} - 1}}{{2x}}} \right] = 3.1 - 2.1 = 1\]
Do đó, thay I=1 vào các đáp án ta được đáp án B.
Đáp án cần chọn là: B
Câu 13:
Cho a là số thực dương khác 1. Xét hai số thực x1, x2. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Vậy khi \[a \ne 1\] thì \[\left( {a - 1} \right)\left( {{x_1} - {x_2}} \right) < 0\]
Đáp án cần chọn là: C
Câu 14:
Cho hàm số \[f\left( x \right) = {2^x}{.7^{{x^2}}}\]. Khẳng định nào sau đây là khẳng định sai?
 Xem đáp án
Xem đáp án
\[\begin{array}{l}f\left( x \right) < 1 \Leftrightarrow {2^x}{.7^{{x^2}}} < 1\\ \Leftrightarrow {7^{{x^2}}} < {2^{ - x}}\\ \Leftrightarrow {x^2}.\ln 7 < - x.\ln 2\\ \Leftrightarrow x\ln 2 + {x^2}\ln 7 < 0\\ \Leftrightarrow x + {x^2}{\log _2}7 < 0\\ \Leftrightarrow x{\log _7}2 + {x^2}\end{array}\]
Đối chiếu các đáp án thấy câu D sai.
Đáp án cần chọn là: D
Câu 15:
Cho các số thực dương a,b khác 1. Biết rằng đường thẳng y=2 cắt đồ thị các hàm số \[y = {a^x};y = {b^x}\;\] và trục tung lần lượt tại A,B,C sao cho C nằm giữa A và B, và AC=2BC. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Ta có: C(0;2)
\[\begin{array}{*{20}{l}}{{a^x} = 2 \Rightarrow x = {{\log }_a}2 \Rightarrow A({{\log }_a}2;2)}\\{{b^x} = 2 \Leftrightarrow x = {{\log }_b}2 \Rightarrow B({{\log }_b}2;2)}\end{array}\]
Vì C nằm giữa A và B và
\[AC = 2BC \Leftrightarrow \overrightarrow {AC} = - 2\overrightarrow {BC} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - lo{g_a}2 = 2.lo{g_b}2}\\{0 = 0}\end{array}} \right. \Leftrightarrow - \frac{1}{{lo{g_2}a}} = 2.\frac{1}{{lo{g_2}b}}\]
\[ \Leftrightarrow lo{g_2}b = - 2lo{g_2}a \Leftrightarrow lo{g_2}b = lo{g_2}{a^{ - 2}} \Leftrightarrow b = {a^{ - 2}}\]
Đáp án cần chọn là: C
Câu 16:
Gọi m là GTLN của hàm số \[f(x) = {e^{{x^3} - 3x + 3}}\;\] trên đoạn \[\left[ {0;2} \right]\]Chọn kết luận đúng:
 Xem đáp án
Xem đáp án
Ta có:
\[f\prime (x) = (3{x^2} - 3){e^{{x^3} - 3x + 3}} = 0 \Leftrightarrow 3{x^2} - 3 = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 \in [0;2]}\\{x = - 1 \notin [0;2]}\end{array}} \right.\)
\[f\left( 0 \right) = {e^3};f\left( 1 \right) = e;f\left( 2 \right) = {e^5}\]nên\[\mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 1 \right) = e\] và\[\mathop {\max }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 2 \right) = {e^5}\]
Vậy\[m = {e^5}\]
Đáp án cần chọn là: D
Câu 17:
Gọi m,M lần lượt là GTNN, GTLN của hàm số \[y = {e^{2 - 3x}}\] trên đoạn \[\left[ {0;2} \right].\]Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:\[f'\left( x \right) = - 3{e^{2 - 3x}} < 0,\forall x \in R\]
Do đó hàm số f(x) lên tục và nghịch biến trên \[\left[ {0;2} \right]\]
Do đó\[m = \mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 2 \right) = \frac{1}{{{e^4}}};M = \mathop {\max }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 0 \right) = {e^2} \Rightarrow M.m = \frac{1}{{{e^2}}}\]
Đáp án cần chọn là: C
</>
Câu 18:
Cho hai số thực dương x,y thỏa mãn \[{2^x} + {2^y} = 4\]. Tìm giá trị lớn nhất PmaxPmax của biểu thức\[P = (2{x^2} + y)(2{y^2} + x) + 9xy\].
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{l}4 = {2^x} + {2^y} \ge 2\sqrt {{2^x}{{.2}^y}} \\ \Rightarrow 2 \ge \sqrt {{2^x}{2^y}} \\ \Rightarrow 4 \ge {2^{x + y}}\\ \Rightarrow 0 < x + y \le 2\\ \Rightarrow {(x + y)^2} \le 4\end{array}\]
Lại có\[x + y \ge 2\sqrt {xy} \Rightarrow xy \le 1\]
\[\begin{array}{*{20}{l}}{ \Rightarrow P = 4{x^2}{y^2} + 2{x^3} + 2{y^3} + 10xy}\\{ = 4{{\left( {xy} \right)}^2} + 10xy + 2\left( {{x^3} + {y^3}} \right)}\\{ = 4{{\left( {xy} \right)}^2} + 10xy}\\{ + 2.\left( {x + y} \right).\left[ {{{\left( {x + y} \right)}^2} - 3xy} \right]}\\{ \Rightarrow P \le 4{{\left( {xy} \right)}^2} + 10xy + 2.2.\left( {4 - 3xy} \right)}\\{ \Rightarrow P \le 4{{\left( {xy} \right)}^2} - 2xy + 16}\end{array}\]
Đặt \[xy = t \Rightarrow 0 < t \le 1\]
Xét hàm số \[f\left( t \right) = 4{t^2} - 2t + 16\] trên\[\left( {0;1} \right]\]
\[ \Rightarrow f\left( t \right) \le \max \left\{ {f\left( 1 \right),f\left( 0 \right)} \right\} = 18\]
Dấu “=” xảy ra khi và chỉ khi x = y = 1.
Vậy\[{P_{\max }} = 18 \Leftrightarrow x = y = 1\]
Đáp án cần chọn là: A
Câu 19:
Cho hàm số \[f(x) = {(3 - \sqrt 2 )^{{x^3}}} - {\left( {3 - \sqrt 2 } \right)^{ - {x^2}}}\]. Xét các khẳng định sau:
Khẳng định 1: \[f(x) > 0 \Leftrightarrow {x^3} + {x^2} > 0\]
Khẳng định 2: \[f(x) > 0 \Leftrightarrow x > - 1\]
Khẳng định 3: \[f(x) < 3 - \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} - 1}} < 1 + {\left( {\frac{{3 + \sqrt 2 }}{7}} \right)^{{x^2} + 1}}\]
Khẳng định 4:\[f(x) < 3 + \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} + 1}} < {(3 - \sqrt 2 )^{1 - {x^2}}} + 7\]
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
 Xem đáp án
Xem đáp án
Cơ số\[3 - \sqrt 2 > 1\]
Ta có
\[f\left( x \right) > 0 \Leftrightarrow {\left( {3 - \sqrt 2 } \right)^{{x^3}}} - {\left( {3 - \sqrt 2 } \right)^{ - {x^2}}} > 0 \Leftrightarrow {x^3} > - {x^2} \Leftrightarrow {x^3} + {x^2} > 0\]
suy ra khẳng định 1 đúng.
Ta có
\[f\left( x \right) > 0 \Leftrightarrow {\left( {3 - \sqrt 2 } \right)^{{x^3}}} - {\left( {3 - \sqrt 2 } \right)^{ - {x^2}}} > 0 \Leftrightarrow {x^3} > - {x^2} \Leftrightarrow {x^3} + {x^2} > 0\]
\[ \Leftrightarrow {x^2}(x + 1) > 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > - 1}\\{x \ne 0}\end{array}} \right.\] suy ra khẳng định 2 sai.
Ta có
\[\begin{array}{l}f(x) < 3 - \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3}}} - {(3 - \sqrt 2 )^{ - {x^2}}} < 3 - \sqrt 2 \\ \Leftrightarrow \frac{{{{(3 - \sqrt 2 )}^{{x^3}}}}}{{3 - \sqrt 2 }} - \frac{{{{(3 - \sqrt 2 )}^{ - {x^2}}}}}{{3 - \sqrt 2 }} < 1\\ \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} - 1}} < 1 + {(3 - \sqrt 2 )^{ - {x^2} - 1}}\\ \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} - 1}} < 1 + {\left( {\frac{1}{{3 - \sqrt 2 }}} \right)^{{x^2} + 1}}\\ \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} - 1}} < 1 + {\left( {\frac{{3 + \sqrt 2 }}{7}} \right)^{{x^2} + 1}}\end{array}\]
suy ra khẳng định 3 đúng.
Ta có
\[\begin{array}{l}f(x) < 3 + \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3}}} - {(3 - \sqrt 2 )^{ - x2}}^{} < 3 + \sqrt 2 \\ \Leftrightarrow {(3 - \sqrt 2 )^{{x^3}}}(3 - \sqrt 2 ) - {(3 - \sqrt 2 )^{ - x2}}(3 - \sqrt 2 ) < (3 + \sqrt 2 )(3 - \sqrt 2 )\\ \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} + 1}} < {(3 - \sqrt 2 )^{1 - x2}} + 7\end{array}\]
Suy ra khẳng định 4 đúng.
Vậy có 3 khẳng định đúng.
Đáp án cần chọn là: B
Câu 20:
Cho hàm số \[f\left( x \right) = \frac{1}{{3 + {2^x}}} + \frac{1}{{3 + {2^{ - x}}}}\]. Trong các khẳng định, có bao nhiêu khẳng định đúng?
1) \[f\prime (x) \ne 0,\forall x \in R\]
2) \[f\left( 1 \right) + f\left( 2 \right) + ... + f\left( {2017} \right) = 2017\]
3) \[f({x^2}) = \frac{1}{{3 + {4^x}}} + \frac{1}{{3 + {4^{ - x}}}}\]
 Xem đáp án
Xem đáp án
Ta có:
\[f'\left( x \right) = \frac{{ - {2^x}\ln 2}}{{{{\left( {3 + {2^x}} \right)}^2}}} + \frac{{{2^{ - x}}\ln 2}}{{{{\left( {3 + {2^{ - x}}} \right)}^2}}} \Rightarrow f'\left( 0 \right) = 0\] nên khẳng định (1) sai.
\[f\left( x \right) = \frac{{{2^x} + {2^{ - x}} + 6}}{{\left( {3 + {2^x}} \right)\left( {3 + {2^{ - x}}} \right)}} = \frac{{{2^x} + {2^{ - x}} + 6}}{{3\left( {{2^x} + {2^{ - x}}} \right) + 10}}\]
Đặt \[t = {2^x} + {2^{ - x}} \ge 2\sqrt {{2^x}{{.2}^{ - x}}} = 2\] thì\[\frac{{{2^x} + {2^{ - x}} + 6}}{{3\left( {{3^x} + {2^{ - x}}} \right) + 10}} = \frac{{t + 6}}{{3t + 10}}\]
Xét\[g\left( t \right) = \frac{{t + 6}}{{3t + 10}},g'\left( t \right) = - \frac{8}{{{{\left( {3t + 10} \right)}^2}}} < 0\] nên hàm số nghịch biến trên\[\left[ {2; + \infty } \right)\]
\[ \Rightarrow g\left( t \right) \le g\left( 2 \right) = \frac{{2 + 6}}{{3.2 + 10}} = \frac{1}{2} < 1\] hay\[f\left( x \right) < 1,\forall x\]
Suy ra\[f\left( 1 \right) < 1,f\left( 2 \right) < 1,...,f\left( {2017} \right) < 1\]
\[ \Rightarrow f\left( 1 \right) + f\left( 2 \right) + ... + f\left( {2017} \right) < 2017\] nên (2) sai.
\[f\left( {{x^2}} \right) = \frac{1}{{3 + {2^{{x^2}}}}} + \frac{1}{{3 + {2^{ - {x^2}}}}} \ne \frac{1}{{3 + {4^x}}} + \frac{1}{{3 + {4^{ - x}}}}\] (chẳng hạn x=1) nên (3) sai.
Do đó không có khẳng định nào đúng.
Đáp án cần chọn là: A
Câu 21:
Tìm tập xác định D của hàm số \[y = \sqrt {1 - {3^{{x^2} - 5x + 6}}} \].
 Xem đáp án
Xem đáp án
Hàm số xác định\[ \Leftrightarrow 1 - {3^{{x^2} - 5x + 6}} \ge 0 \Leftrightarrow {3^{{x^2} - 5x + 6}} \le 1\]
\[ \Leftrightarrow {x^2} - 5x + 6 \le 0 \Leftrightarrow 2 \le x \le 3\]
Vậy tập xác định của hàm số là\[D = [2;3]\]
Đáp án cần chọn là: A
Câu 22:
Tính đạo hàm của hàm số \[y = f\left( x \right) = {x^\pi }.{\pi ^x}\] tại điểm x=1.
 Xem đáp án
Xem đáp án
Đạo hàm\[f'\left( x \right) = {\left( {{x^\pi }} \right)^\prime }.{\pi ^x} + {x^\pi }.{\left( {{\pi ^x}} \right)^\prime } = \pi .{x^{\pi - 1}}.{\pi ^x} + {x^\pi }.{\pi ^x}.\ln \pi \]
Suy ra \[f'\left( 1 \right) = {\pi ^2} + \pi \ln \pi \]
Đáp án cần chọn là: C
Câu 23:
Tập tất cả các giá trị của tham số a để hàm số \[y = {\left( {a - 2} \right)^x}\] nghịch biến trên \(\mathbb{R}\) là:
 Xem đáp án
Xem đáp án
Hàm số \[y = {\left( {a - 2} \right)^x}\] nghịch biến trên \(\mathbb{R}\) khi và chỉ khi \[0 < a - 2 < 1 \Leftrightarrow 2 < a < 3\]
Vậy tập các giá trị của tham số aa để hàm số đã cho nghịch biến trên \(\mathbb{R}\) là (2;3).
Đáp án cần chọn là: C
Câu 24:
Hàm số nào sau đây nghịch biến trên \[\left( { - \infty ; + \infty } \right)\]?
 Xem đáp án
Xem đáp án
Do \[0 < \frac{2}{e} < 1\]nên hàm số \[y = {\left( {\frac{2}{e}} \right)^x}\] nghịch biến trên\[\left( { - \infty ; + \infty } \right)\]Đáp án cần chọn là: C
Câu 25:
Tính đạo hàm của hàm số \[y = {6^x}\]
 Xem đáp án
Xem đáp án
\[y = {6^x} \Rightarrow y' = {6^x}\ln 6.\]
Đáp án cần chọn là: B
Câu 26:
Tập xác định của hàm số \[y = {2^x}\] là:
 Xem đáp án
Xem đáp án
Tập xác định của hàm số \[y = {2^{x\;}}\] là \(\mathbb{R}\).
Đáp án cần chọn là: B
Câu 27:
Cho hàm số \[y = {e^{2x}} - x\]Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
TXĐ: \[D = \mathbb{R}\]
Ta có:\[y' = 2{e^{2x}} - 1 = 0 \Leftrightarrow {e^{2x}} = \frac{1}{2}\]
\[ \Leftrightarrow 2x = \ln \frac{1}{2} = - \ln 2 \Leftrightarrow x = - \frac{1}{2}\ln 2 = - \ln \sqrt 2 \]
BBT:
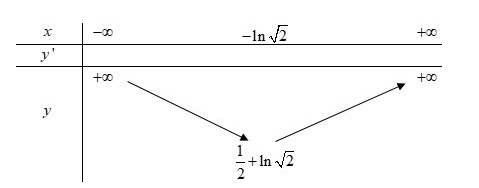
Dựa vào BBT ta thấy hàm số đồng biến trên \[\left( { - \ln \sqrt 2 ; + \infty } \right)\]Đáp án cần chọn là: A
Câu 28:
Tìm tất cả các giá trị thực của m để hàm số \[y = {2^{{x^3} - {x^2} + mx + 1}}\] đồng biến trên (1;2)
 Xem đáp án
Xem đáp án
Ta có:\[y = {2^{{x^3} - {x^2} + mx + 1}} \Rightarrow y' = \left( {3{x^2} - 2x + m} \right){2^{{x^3} - {x^2} + mx + 1}}\]
⇒ Hàm số đã cho đồng biến trên\[\left( {1;\,\,2} \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {1;\,\,2} \right)\]
\[ \Leftrightarrow (3{x^2} - 2x + m){2^{{x^3} - x2 + mx + 1}} \ge 0\forall x \in (1;2)\]
\[ \Leftrightarrow 3{x^2} - 2x + m \ge 0\forall x \in (1;2)\]
\( \Leftrightarrow {\left[ {\begin{array}{*{20}{c}}{\Delta \prime \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{\Delta \prime \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{{x_1} < {x_2} \le 1}\\{2 \le {x_1} < x2}\end{array}} \right.}\end{array}} \right.}\end{array}} \right._{}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\Delta \prime \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{\Delta \prime \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} < 2}\\{({x_1} - 1)({x_2} - 1) \ge 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} > 4}\\{({x_1} - 1)({x_2} - 1) \ge 0}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.\)</>
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\Delta \prime \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{\Delta \prime \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} < 2}\\{{x_1}{x_2} - ({x_1} + {x_2}) + 1 \ge 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} > 4}\\{{x_1}{x_2} - ({x_1} + {x_2}) + 1 \ge 0}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.\)</>
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 - 3m \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{1 - 3m \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{\frac{2}{3} < 2}\\{\frac{m}{3} - \frac{2}{3} + 1 \ge 0}\end{array}} \right.}\\{\left[ {\begin{array}{*{20}{c}}{\frac{x}{3} > 4(ktm)}\\{\frac{m}{3} - \frac{4}{3} + 4 \ge 0}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.\)</>
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{m \ge \frac{1}{3}}\\{\left\{ {\begin{array}{*{20}{c}}{m \le \frac{1}{3}}\\{\frac{m}{3} \ge - \frac{1}{3}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge \frac{1}{3}}\\{\left\{ {\begin{array}{*{20}{c}}{m \le \frac{1}{3}}\\{m \ge - 1}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge \frac{1}{3}}\\{ - 1 \le m \le \frac{1}{3}}\end{array} \Leftrightarrow m \ge - 1.} \right.\)
Đáp án cần chọn là: B
