Tìm tất cả các giá trị thực của m để hàm số \[y = {2^{{x^3} - {x^2} + mx + 1}}\] đồng biến trên (1;2)
A.\[m > - 8.\]
B. \[m \ge - 1.\]
C. \[m \le - 8.\]
D. \[m < - 1.\]
Giải bởi Vietjack
Ta có:\[y = {2^{{x^3} - {x^2} + mx + 1}} \Rightarrow y' = \left( {3{x^2} - 2x + m} \right){2^{{x^3} - {x^2} + mx + 1}}\]
⇒ Hàm số đã cho đồng biến trên\[\left( {1;\,\,2} \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {1;\,\,2} \right)\]
\[ \Leftrightarrow (3{x^2} - 2x + m){2^{{x^3} - x2 + mx + 1}} \ge 0\forall x \in (1;2)\]
\[ \Leftrightarrow 3{x^2} - 2x + m \ge 0\forall x \in (1;2)\]
\( \Leftrightarrow {\left[ {\begin{array}{*{20}{c}}{\Delta \prime \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{\Delta \prime \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{{x_1} < {x_2} \le 1}\\{2 \le {x_1} < x2}\end{array}} \right.}\end{array}} \right.}\end{array}} \right._{}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\Delta \prime \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{\Delta \prime \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} < 2}\\{({x_1} - 1)({x_2} - 1) \ge 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} > 4}\\{({x_1} - 1)({x_2} - 1) \ge 0}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.\)</>
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\Delta \prime \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{\Delta \prime \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} < 2}\\{{x_1}{x_2} - ({x_1} + {x_2}) + 1 \ge 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} > 4}\\{{x_1}{x_2} - ({x_1} + {x_2}) + 1 \ge 0}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.\)</>
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 - 3m \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{1 - 3m \ge 0}\\{\left[ {\begin{array}{*{20}{c}}{\frac{2}{3} < 2}\\{\frac{m}{3} - \frac{2}{3} + 1 \ge 0}\end{array}} \right.}\\{\left[ {\begin{array}{*{20}{c}}{\frac{x}{3} > 4(ktm)}\\{\frac{m}{3} - \frac{4}{3} + 4 \ge 0}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.\)</>
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{m \ge \frac{1}{3}}\\{\left\{ {\begin{array}{*{20}{c}}{m \le \frac{1}{3}}\\{\frac{m}{3} \ge - \frac{1}{3}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge \frac{1}{3}}\\{\left\{ {\begin{array}{*{20}{c}}{m \le \frac{1}{3}}\\{m \ge - 1}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge \frac{1}{3}}\\{ - 1 \le m \le \frac{1}{3}}\end{array} \Leftrightarrow m \ge - 1.} \right.\)
Đáp án cần chọn là: B
Hàm số nào sau đây nghịch biến trên \[\left( { - \infty ; + \infty } \right)\]?
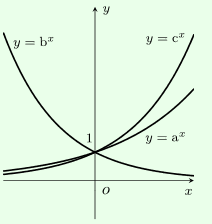
Cho các đồ thị hàm số \[y = {a^x},y = {b^x},y = {c^x}(0 < a,b,c \ne 1)\] chọn khẳng định đúng:
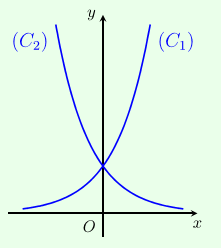
Cho hai hàm số \[y = {a^x},y = {b^x}\] với \[1 \ne a,b > 0\;\]lần lượt có đồ thị là (C1),(C2) như hình bên. Mệnh đề nào đúng?
Cho a là số thực dương khác 1. Xét hai số thực x1, x2. Phát biểu nào sau đây là đúng?
Cho hàm số \[f(x) = {(3 - \sqrt 2 )^{{x^3}}} - {\left( {3 - \sqrt 2 } \right)^{ - {x^2}}}\]. Xét các khẳng định sau:
Khẳng định 1: \[f(x) > 0 \Leftrightarrow {x^3} + {x^2} > 0\]
Khẳng định 2: \[f(x) > 0 \Leftrightarrow x > - 1\]
Khẳng định 3: \[f(x) < 3 - \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} - 1}} < 1 + {\left( {\frac{{3 + \sqrt 2 }}{7}} \right)^{{x^2} + 1}}\]
Khẳng định 4:\[f(x) < 3 + \sqrt 2 \Leftrightarrow {(3 - \sqrt 2 )^{{x^3} + 1}} < {(3 - \sqrt 2 )^{1 - {x^2}}} + 7\]
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
Cho các số thực dương a,b khác 1. Biết rằng đường thẳng y=2 cắt đồ thị các hàm số \[y = {a^x};y = {b^x}\;\] và trục tung lần lượt tại A,B,C sao cho C nằm giữa A và B, và AC=2BC. Khẳng định nào dưới đây đúng?
Cho hàm số \[f\left( x \right) = \frac{1}{{3 + {2^x}}} + \frac{1}{{3 + {2^{ - x}}}}\]. Trong các khẳng định, có bao nhiêu khẳng định đúng?
1) \[f\prime (x) \ne 0,\forall x \in R\]
2) \[f\left( 1 \right) + f\left( 2 \right) + ... + f\left( {2017} \right) = 2017\]
3) \[f({x^2}) = \frac{1}{{3 + {4^x}}} + \frac{1}{{3 + {4^{ - x}}}}\]
