Nghiệm của phương trình \[\cos 3x = \cos x\] là:
A.\[k2\pi \left( {k \in Z} \right)\]
B. \[k2\pi ;\frac{\pi }{2} + k2\pi \left( {k \in Z} \right)\]
C. \[\frac{{k\pi }}{2}\left( {k \in Z} \right)\]
D. \[k\pi ;\frac{\pi }{2} + k2\pi \left( {k \in Z} \right)\]
Giải bởi Vietjack
Bước 1:
Ta có:
\[cos3x = cosx \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = x + k2\pi }\\{3x = - x + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = k2\pi }\\{4x = k2\pi }\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\pi }\\{x = \frac{{k\pi }}{2}}\end{array}} \right.} \right.\]
Bước 2:
+) Với họ nghiệm \[x = k\pi \] ta có:
Khi k=0 thì x=0, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k chẵn)
Khi k=1 thì \[x = \pi \], điểm biểu diễn là A' (Vẫn là điểm đó khi k lẻ).
Như thế họ nghiệm \[x = k\pi \] có 2 điểm biểu diễn là A,A′.
+) Với họ nghiệm\[x = \frac{{k\pi }}{2}\] ta có:
Khi k=0 thì x=0, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k có dạng 4m, tức là k chia hết cho 4)
Khi k=1 thì \[x = \frac{\pi }{2}\] điểm biểu diễn là B (Vẫn là điểm đó khi k có dạng 4m+1).
Khi k=2 thì \[x = \pi \] điểm biểu diễn là A' (Vẫn là điểm đó khi k có dạng 4m+2).
Khi k=3 thì\[x = \frac{{3\pi }}{2}\] điểm biểu diễn là B' (Vẫn là điểm đó khi k có dạng 4m+3).
Như thế họ nghiệm\[x = \frac{{k\pi }}{2}\] có 44 điểm biểu diễn là A,A′,B,B′.
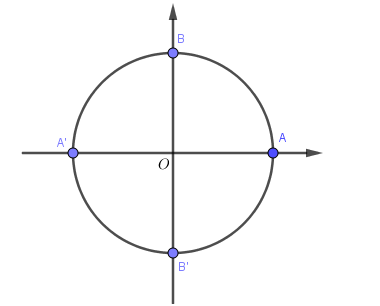
+) Kết hợp các điểm này lại ta được tổng cộng vẫn là 4 điểm A,A′,B,B′. Mà 4 điểm này là 4 điểm biểu diễn của chính họ nghiệm\[x = \frac{{k\pi }}{2}\] nên nghiệm của phương trình ban đầu là \[x = \frac{{k\pi }}{2}k \in Z\]
Đáp án cần chọn là: C
Phương trình lượng giác \[\frac{{\cos x - \frac{{\sqrt 3 }}{2}}}{{\sin x - \frac{1}{2}}} = 0\] có nghiệm là:
Với giá trị nào của m dưới đây thì phương trình sinx = m có nghiệm?
Phương trình \[\sin \left( {2x + \frac{\pi }{7}} \right) = {m^2} - 3m + 3\] vô nghiệm khi:
Phương trình \[\sqrt 3 \cot \left( {5x - \frac{\pi }{8}} \right) = 0\]có nghiệm là:
Nghiệm của phương trình \[\sin x = \frac{1}{2}\] thỏa mãn \[ - \frac{\pi }{2} \le x \le \frac{\pi }{2}\] là:
Phương trình \[\cot 20x = 1\] có bao nhiêu nghiệm thuộc khoảng \[\left[ { - 50\pi ;0} \right]?\]
Phương trình \[\tan \left( {\frac{\pi }{2} - x} \right) + 2\tan \left( {2x + \frac{\pi }{2}} \right) = 1\] có nghiệm là:
Giải phương trình lượng giác \[\sin \left( {\frac{\pi }{3} - 3x} \right) = \sin \left( {x + \frac{\pi }{4}} \right)\] có nghiệm là:
Số nghiệm của phương trình \[\cos 2x = \frac{1}{2}\] trên nửa khoảng \[({0^0};{36^0}]\;\]là?
Số nghiệm của phương trình \[2\sin \left( {x + \frac{\pi }{4}} \right) - 2 = 0\]với \[\pi \le x \le 5\pi \]là:
Nghiệm của phương trình \[\tan \left( {2x - {{15}^0}} \right) = 1\], với \[ - {90^0} < x < {90^0}\;\]là:
