Trong không gian \[Oxyz,\] để phương trình \({x^2} + {y^2} + {z^2} - 2\left( {m + 2} \right)x + 4my + 19m - 6 = 0\) là phương trình mặt cầu thì tất cả các giá trị của tham số \(m\) là
A. \(1 < m < 2.\)
B. \(m < 1\) hoặc \(m > 2.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có \({x^2} + {y^2} + {z^2} - 2\left( {m + 2} \right)x + 4my + 19m - 6 = 0\)
\[ \Leftrightarrow {\left( {x - m - 2} \right)^2} + {\left( {y + 2m} \right)^2} + {z^2} = {\left( {m + 2} \right)^2} + 4{m^2} - 19m + 6\]
Yêu cầu bài toán trở thành: \({\left( {m + 2} \right)^2} + 4{m^2} - 19m + 6 > 0\)
\( \Leftrightarrow 5{m^2} - 15m + 10 > 0 \Leftrightarrow m < 1\) hoặc \(m > 2.\) Chọn B.
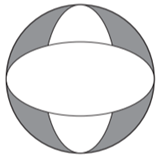
Cho đường tròn có đường kính bằng 4 và 2 Elip lần lượt nhận 2 đường kính vuông góc với nhau của đường tròn làm trục lớn, trục bé của mỗi Elip đều bằng 1. Diện tích \[S\] phần hình phẳng ở bên trong đường tròn và bên ngoài 2 Elip (phần gạch tô màu trên hình vẽ) gần với kết quả nào nhất trong 4 kết quả dưới đây?
Cho hàm số \(f\left( x \right) = 2{x^2} - 4x - 2.\) Gọi \(S\) là tống tất cả các giá trị của tham số \(m\) để hàm số \(y = g\left( x \right) = \left| {{f^2}\left( x \right) - 2f\left( x \right) + m} \right|\) đạt giá trị lớn nhất trên đoạn \(\left[ { - 1\,;\,\,3} \right]\) bằng 15. Tổng \(S\) thuộc khoảng nào sau đây?
Các hình dưới đây biểu diễn dung dịch nước của ba acid \({\rm{HA}}\,({\rm{A}} = {\rm{X}},{\rm{Y}},{\rm{Z}})\); bỏ qua sự phân li của nước.
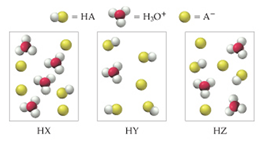
Các dung dịch đều có cùng nồng độ, dung dịch nào dẫn điện tốt nhất?
Cho tập hợp \(A = \left[ {4\,;\,\,7} \right]\) và \(B = \left[ {2a + 3b - 1\,;\,\,3a - b + 5} \right]\) với \(a,\,\,b \in \mathbb{R}.\) Khi \(A = B\) thì giá trị biểu thức \(M = {a^2} + {b^2}\) bằng
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở A, B khác tiếp điểm. Tính độ dài đoạn thẳng AB ?
Hỗn hợp X gồm ba ester đơn chức đều có công thức phân tử \({{\rm{C}}_8}{{\rm{H}}_8}{{\rm{O}}_2}\); chứa vòng benzene (vòng benzene chỉ có một nhóm thế) và một ester hai chức là ethyl phenyl oxalate. Thủy phân hoàn toàn 7,38 gam X trong lượng dư dung dịch \({\rm{NaOH}}\), thấy có \(0,08\;{\rm{mol}}\,\,{\rm{NaOH}}\) phản ứng, thu được \({\rm{m}}\) gam hỗn hợp muối và 2,18 gam hỗn hợp alcohol Y. Cho toàn bộ Y tác dụng với Na dư, thu được 0,4958 lít khí \({{\rm{H}}_2}\)(đkc). Giá trị của m là
Đáp án: ……….
Trên mặt phẳng với hệ tọa độ Oxy, cho ba đường thẳng lần lượt có phương trình \({d_1}:3x - 4y + 15 = 0,\,\,{d_2}:5x + 2y - 1 = 0\) và \({d_3}:mx - \left( {2m - 1} \right)y + 9m - 13 = 0.\) Tất cả các giá trị của tham số \(m\) để ba đường thẳng đã cho cùng đi qua một điểm là
Đọc đoạn trích sau đây và trả lời câu hỏi:
Cúng mẹ và cơm nước xong, mấy chị em, chú cháu thu xếp đồ đạc dời nhà. Chị Chiến ra đằng giữa sân, kéo cái khăn trên cổ xuống, cũng xắn tay áo để lộ hai bắp tay tròn vo sạm đỏ màu cháy nắng, rồi dùng cả thân người to và chắc nịch của mình nhấc bổng một đầu bàn thờ má lên. Việt ghé vào một đầu. Nào, đưa má sang ở tạm bên nhà chú, chúng con đi đánh giặc trả thù cho ba má, đến chừng nước nhà độc lập con lại đưa má về. Việt khiêng trước. Chị Chiến khiêng bịch bịch phía sau. Nghe tiếng chân chị, Việt thấy thương chị lạ. Lần đầu tiên Việt mới thấy lòng mình rõ như thế. Còn mối thù thằng Mĩ thì có thể sờ thấy được, vì nó đang đè nặng ở trên vai.
(Những đứa con trong gia đình – Nguyễn Thi)
Đặc điểm tính cách nào ở nhân vật Việt được thể hiện trong đoạn trích trên?
Trong không gian \[Oxyz,\] cho \(\overrightarrow {OA} = \vec i - 2\vec j + 3\vec k\), điểm \(B\left( {3\,;\, - 4\,;\,1} \right)\) và điểm \[C\left( {2\,;\,\,0\,;\,\, - 1} \right).\] Tọa độ trọng tâm của tam giác \[ABC\] là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)