Trong không gian \[Oxyz,\] cho đường thẳng \(\Delta :\frac{x}{1} = \frac{{y - 1}}{1} = \frac{{z + 2}}{{ - 2}}\) và ba điểm \[A\left( {1\,;\,\,3\,;\,\, - 2} \right),\]\[B\left( {0\,;\,\,4\,;\,\, - 5} \right),\,\,C\left( {1\,;\,\,2\,;\,\, - 4} \right)\]. Biết điểm \[M\left( {a\,;\,\,b\,;\,\,c} \right)\] thuộc đường thẳng \(\Delta \) sao cho \(M{A^2} + M{B^2} + 2M{C^2}\) đạt giá trị nhỏ nhất. Khi đó, giá trị của \(a + b + c\) bằng
A. 0
B. -1
C. 3
D. 4
 Giải bởi Vietjack
Giải bởi Vietjack
Vì \[M \in \Delta \Rightarrow M\left( {t\,;\,\,1 + t\,;\,\, - 2 - 2t} \right)\] nên ta có
• \[M{A^2} = {\left( {1 - t} \right)^2} + {\left( {2 - t} \right)^2} + {\left( {2t} \right)^2} = 6{t^2} - 6t + 5\]
• \(M{B^2} = {\left( { - t} \right)^2} + {\left( {3 - t} \right)^2} + {\left( { - 3 + 2t} \right)^2} = 6{t^2} - 18t + 18;\)
• \(M{C^2} = {\left( {1 - t} \right)^2} + {\left( {1 - t} \right)^2} + {\left( { - 2 + 2t} \right)^2} = 6{t^2} - 12t + 6 \Rightarrow 2M{C^2} = 12{t^2} - 24t + 12.\)
Suy ra \(M{A^2} + M{B^2} + 2M{C^2} = 24{t^2} - 48t + 35 = 24\left( {{t^2} - 2t + 1} \right) + 11 = 24{\left( {t - 1} \right)^2} + 11 \ge 11\)
Nên \(M{A^2} + M{B^2} + 2M{C^2}\) đạt giá trị nhỏ nhất khi và chỉ khi \(t = 1\).
Do đó \[M\left( {1\,;\,\,2\,;\,\, - 4} \right)\] nên \(a = 1\,;\,\,b = 2\,;\,\,c = - 4.\) Vậy \(a + b + c = - 1.\) Chọn B.
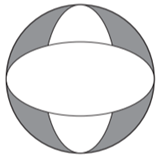
Cho đường tròn có đường kính bằng 4 và 2 Elip lần lượt nhận 2 đường kính vuông góc với nhau của đường tròn làm trục lớn, trục bé của mỗi Elip đều bằng 1. Diện tích \[S\] phần hình phẳng ở bên trong đường tròn và bên ngoài 2 Elip (phần gạch tô màu trên hình vẽ) gần với kết quả nào nhất trong 4 kết quả dưới đây?
Cho hàm số \(f\left( x \right) = 2{x^2} - 4x - 2.\) Gọi \(S\) là tống tất cả các giá trị của tham số \(m\) để hàm số \(y = g\left( x \right) = \left| {{f^2}\left( x \right) - 2f\left( x \right) + m} \right|\) đạt giá trị lớn nhất trên đoạn \(\left[ { - 1\,;\,\,3} \right]\) bằng 15. Tổng \(S\) thuộc khoảng nào sau đây?
Các hình dưới đây biểu diễn dung dịch nước của ba acid \({\rm{HA}}\,({\rm{A}} = {\rm{X}},{\rm{Y}},{\rm{Z}})\); bỏ qua sự phân li của nước.
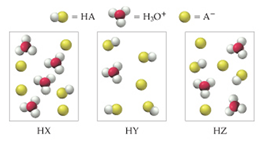
Các dung dịch đều có cùng nồng độ, dung dịch nào dẫn điện tốt nhất?
Cho tập hợp \(A = \left[ {4\,;\,\,7} \right]\) và \(B = \left[ {2a + 3b - 1\,;\,\,3a - b + 5} \right]\) với \(a,\,\,b \in \mathbb{R}.\) Khi \(A = B\) thì giá trị biểu thức \(M = {a^2} + {b^2}\) bằng
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở A, B khác tiếp điểm. Tính độ dài đoạn thẳng AB ?
Hỗn hợp X gồm ba ester đơn chức đều có công thức phân tử \({{\rm{C}}_8}{{\rm{H}}_8}{{\rm{O}}_2}\); chứa vòng benzene (vòng benzene chỉ có một nhóm thế) và một ester hai chức là ethyl phenyl oxalate. Thủy phân hoàn toàn 7,38 gam X trong lượng dư dung dịch \({\rm{NaOH}}\), thấy có \(0,08\;{\rm{mol}}\,\,{\rm{NaOH}}\) phản ứng, thu được \({\rm{m}}\) gam hỗn hợp muối và 2,18 gam hỗn hợp alcohol Y. Cho toàn bộ Y tác dụng với Na dư, thu được 0,4958 lít khí \({{\rm{H}}_2}\)(đkc). Giá trị của m là
Đáp án: ……….
Trên mặt phẳng với hệ tọa độ Oxy, cho ba đường thẳng lần lượt có phương trình \({d_1}:3x - 4y + 15 = 0,\,\,{d_2}:5x + 2y - 1 = 0\) và \({d_3}:mx - \left( {2m - 1} \right)y + 9m - 13 = 0.\) Tất cả các giá trị của tham số \(m\) để ba đường thẳng đã cho cùng đi qua một điểm là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)