Cho hình chóp \[S.ABCD\] có đáy là hình chữ nhật, cạnh \(AB = 2AD = a.\) Tam giác \[SAB\] đều và nằm trong mặt phẳng vuông góc với đáy \(\left( {ABCD} \right).\) Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBD} \right)\) bằng
Giải bởi Vietjack
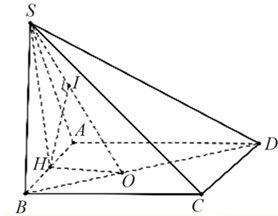
Gọi \(H\) là trung điểm của \[AB.\]
Từ giả thiết, suy ra \(SH \bot \left( {ABCD} \right).\)
Từ \(H\) kẻ \(HG \bot BD\) tại \(G\), kẻ \(HI \bot SG\) tại I.
Suy ra \[HI \bot \left( {SBD} \right) \Rightarrow d\left( {H,\,\,\left( {SBD} \right)} \right) = HI.\]
Ta có \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2},SH = \frac{{a\sqrt 3 }}{2}.\)Lại có nên \(\frac{{HG}}{{AD}} = \frac{{BH}}{{BD}} \Rightarrow HG = \frac{{AD \cdot BH}}{{BD}} = \frac{{\frac{a}{2} \cdot \frac{a}{2}}}{{\frac{{a\sqrt 5 }}{2}}} = \frac{{a\sqrt 5 }}{{10}}.\)
Khi đó \(\frac{1}{{H{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{G^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 5 }}{{10}}} \right)}^2}}}\). Suy ra \(HI = \frac{{a\sqrt 3 }}{8}.\)
Lại có \(d\left( {A,\,\,\left( {SBD} \right)} \right) = 2d\left( {H,\,\,\left( {SBD} \right)} \right) = 2 \cdot HI = 2 \cdot \frac{{a\sqrt 3 }}{8} = \frac{{a\sqrt 3 }}{4}.\) Chọn A.
Ông Khoa muốn xây dựng một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng \[288{\rm{ }}{m^3}.\] Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là \[500\,\,000\] đồng/\[{m^2}.\] Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông Khoa phải trả chi phí thấp nhất bao nhiêu triệu đồng để xây dựng bế đó (biết độ dày thành bể và đáy bể không đáng kể)?
Một số có ba chữ số. Nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 17 và dư 7. Nếu đổi hai chữ số hàng chục và hàng trăm cho nhau thì được số mới mà chia cho tổng các chữ số của nó thì được thương là 54 và dư 8. Nếu đổi hai chữ số hàng chục và hàng đơn vị của số mới này cho nhau thì được một số mà chia cho tổng các chữ số của nó thì được thương là 15 và dư là 14. Vậy số đã cho ban đầu là
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 25\,;\,\,25} \right]\) sao cho đồ thị hàm số \(y = \frac{{x - 1}}{{{x^2} - 2mx + 3m + 10}}\) có đúng 2 đường tiệm cận đứng?
Trong một lần đến tham quan tượng Nữ thần tự do (Ở Newyork, Mỹ), bạn Hưng muốn ước tính độ cao của tượng. Sau khi quan sát, bạn Hưng đã minh họa lại kết quả đo đạc như hình dưới đây:
Nếu chiều cao h của tượng được làm tròn đến chữ số thập phân thứ nhất thì h bằng:
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Chiều 26/12, tại Hà Nội, Ủy ban An toàn giao thông Quốc gia tổ chức Lễ trao giải thưởng báo chí tuyên truyền về an toàn giao thông năm 2022; phát động giải thưởng năm 2023,… Giải Nhất thể loại Báo hình đã được _______ cho các loạt phóng sự điều tra “Xe dù, bến cóc” của nhóm tác giả: Lưu Thoan, Thúy Nga, Văn Bình, Tiến Thành của Truyền hình Thông tấn, Thông tấn xã Việt Nam.
Đọc đoạn trích sau đây và trả lời câu hỏi:
Mơ khách đường xa, khách đường xa
Áo em trắng quá nhìn không ra
Ở đây sương khói mờ nhân ảnh
Ai biết tình ai có đậm đà ?
(Trích Đây thôn Vĩ Dạ – Hàn Mặc Tử)
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho tứ diện \[ABCD\] có \[A\left( {2\,;\,\, - 1\,;\,\,1} \right),\,\]\[\,B\left( {3\,;\,\,0\,;\,\, - 1} \right),\]\[C\left( {2\,;\,\, - 1\,;\,\,3} \right),\,\,D \in Oy\] và có thể tích bằng 5. Tổng tung độ của các điểm \(D\) là
PHẦN 3: KHOA HỌC
Lĩnh vực: Khoa học tự nhiên và xã hội (50 câu – 60 phút)
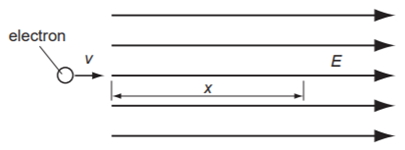
Một electron có điện tích e, khối lượng m, vận tốc v đi vào một điện trường đều có cường độ điện trường E như hình vẽ. Quãng đường x mà electron đi được ngay trước khi dừng lại là
Một loài động vật có 4 cặp NST được kí hiệu là Aa, Bb, Dd và Ee. Trong các cơ thể có bộ NST sau đây, có bao nhiêu thể ba?
I. AaaBbDdEe.
II. ABbDdEe.
III. AaBBbDdEe.
IV. AaBbDdEe.
V. AaBbDdEEe.
VI. AaBbDddEe.
Ở một loài thực vật tự thụ phấn, xét hai cặp gen Aa và Bb, trong đó alen A quy định cây thân cao, alen a quy định cây thân thấp, alen B quy định quả đỏ, alen b quy định quả vàng, các gen phân li độc lập. Một quần thể (P) của loài này có tỉ lệ các kiểu gen như sau:
|
Kiểu gen |
AABb |
AaBb |
Aabb |
aaBb |
aabb |
|
Tỉ lệ |
0,36 |
0,24 |
0,18 |
0,12 |
0,1 |
Biết rằng không xảy ra đột biến ở tất cả các cá thể trong quần thể, các cá thể tự thụ phấn nghiêm ngặt. Theo lí thuyết, cây mang hai cặp gen dị hợp trong quần thể ở thế hệ F1 chiếm tỉ lệ là bao nhiêu?
Đáp án: ……….
Người ta trồng \[3\,\,240\] cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng thứ hai trở đi số cây trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi có tất cả bao nhiêu hàng cây?
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \[2a,\] cạnh bên tạo với đáy một góc \(60^\circ .\) Thể tích khối chóp \(S.ABC\) là
