Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rắng: Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ có cân nặng là \(P\left( n \right) = 360 - 10n.\) Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất?
Giải bởi Vietjack
Điều kiện \(\left\{ {\begin{array}{*{20}{l}}{360 - 10n > 0}\\{n \in {\mathbb{N}^*}}\end{array} \Leftrightarrow 0 < n < 36} \right..\)
Trọng lượng cá trên một đơn vị diện tích là:
\(T = \left( {360 - 10n} \right)n = - 10{n^2} + 360n = - 10{\left( {n - 18} \right)^2} + 3\,\,240 \Rightarrow T \le 3\,\,240.{\rm{ }}\)
Dấu "=" xảy ra khi \(n = 18\) (nhận). Do đó \({T_{\max }} = 3\,\,240 \Leftrightarrow n = 18.\)
Vậy cẩn thả 18 con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất.
Đáp án: 18.
Ông Khoa muốn xây dựng một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng \[288{\rm{ }}{m^3}.\] Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là \[500\,\,000\] đồng/\[{m^2}.\] Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông Khoa phải trả chi phí thấp nhất bao nhiêu triệu đồng để xây dựng bế đó (biết độ dày thành bể và đáy bể không đáng kể)?
Một số có ba chữ số. Nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 17 và dư 7. Nếu đổi hai chữ số hàng chục và hàng trăm cho nhau thì được số mới mà chia cho tổng các chữ số của nó thì được thương là 54 và dư 8. Nếu đổi hai chữ số hàng chục và hàng đơn vị của số mới này cho nhau thì được một số mà chia cho tổng các chữ số của nó thì được thương là 15 và dư là 14. Vậy số đã cho ban đầu là
Trong một lần đến tham quan tượng Nữ thần tự do (Ở Newyork, Mỹ), bạn Hưng muốn ước tính độ cao của tượng. Sau khi quan sát, bạn Hưng đã minh họa lại kết quả đo đạc như hình dưới đây:
Nếu chiều cao h của tượng được làm tròn đến chữ số thập phân thứ nhất thì h bằng:
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 25\,;\,\,25} \right]\) sao cho đồ thị hàm số \(y = \frac{{x - 1}}{{{x^2} - 2mx + 3m + 10}}\) có đúng 2 đường tiệm cận đứng?
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho tứ diện \[ABCD\] có \[A\left( {2\,;\,\, - 1\,;\,\,1} \right),\,\]\[\,B\left( {3\,;\,\,0\,;\,\, - 1} \right),\]\[C\left( {2\,;\,\, - 1\,;\,\,3} \right),\,\,D \in Oy\] và có thể tích bằng 5. Tổng tung độ của các điểm \(D\) là
Biết \[x\,,\,\,y\] là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2\left( {{x^2} - 2x} \right) + \sqrt {y + 1} = 0}\\{3\left( {{x^2} - 2x} \right) - 2\sqrt {y + 1} = - 7}\end{array}} \right..\) Để \(mx + 2y = 4\) thì giá trị \(m\) nào sau đây thỏa mãn?
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Chiều 26/12, tại Hà Nội, Ủy ban An toàn giao thông Quốc gia tổ chức Lễ trao giải thưởng báo chí tuyên truyền về an toàn giao thông năm 2022; phát động giải thưởng năm 2023,… Giải Nhất thể loại Báo hình đã được _______ cho các loạt phóng sự điều tra “Xe dù, bến cóc” của nhóm tác giả: Lưu Thoan, Thúy Nga, Văn Bình, Tiến Thành của Truyền hình Thông tấn, Thông tấn xã Việt Nam.
Đọc đoạn trích sau đây và trả lời câu hỏi:
Mơ khách đường xa, khách đường xa
Áo em trắng quá nhìn không ra
Ở đây sương khói mờ nhân ảnh
Ai biết tình ai có đậm đà ?
(Trích Đây thôn Vĩ Dạ – Hàn Mặc Tử)
PHẦN 3: KHOA HỌC
Lĩnh vực: Khoa học tự nhiên và xã hội (50 câu – 60 phút)
Ở một loài thực vật tự thụ phấn, xét hai cặp gen Aa và Bb, trong đó alen A quy định cây thân cao, alen a quy định cây thân thấp, alen B quy định quả đỏ, alen b quy định quả vàng, các gen phân li độc lập. Một quần thể (P) của loài này có tỉ lệ các kiểu gen như sau:
|
Kiểu gen |
AABb |
AaBb |
Aabb |
aaBb |
aabb |
|
Tỉ lệ |
0,36 |
0,24 |
0,18 |
0,12 |
0,1 |
Biết rằng không xảy ra đột biến ở tất cả các cá thể trong quần thể, các cá thể tự thụ phấn nghiêm ngặt. Theo lí thuyết, cây mang hai cặp gen dị hợp trong quần thể ở thế hệ F1 chiếm tỉ lệ là bao nhiêu?
Đáp án: ……….
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \[2a,\] cạnh bên tạo với đáy một góc \(60^\circ .\) Thể tích khối chóp \(S.ABC\) là
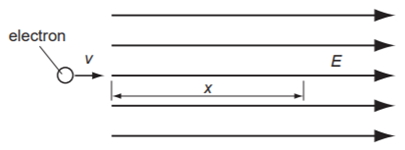
Một electron có điện tích e, khối lượng m, vận tốc v đi vào một điện trường đều có cường độ điện trường E như hình vẽ. Quãng đường x mà electron đi được ngay trước khi dừng lại là
