 Giải bởi Vietjack
Giải bởi Vietjack
Để trả lời được câu hỏi này học sinh phải nắm chắc được khái niệm về các cách thức hay còn gọi là quy tắc lập luận của đoạn văn. Trong đó, đặc điểm của quy tắc/cách thức “tổng - phân – hợp” là có câu chủ đề ở đầu đoạn “Con người lo lắng rằng khi AI trở nên phát triển hơn, chúng ta sẽ dựa vào máy tính của mình nhiều đến mức cuối cùng sẽ coi chúng là bạn và không thể hoạt động nếu không có chúng.” và câu khái quát, nâng cao ý ở cuối đoạn “Nhưng có lẽ một trong những hệ quả sâu xa nhất của nó sẽ là khiến chúng ta phải trân trọng những điều con người nhất trong ta”. Đọc kĩ đoạn văn (2) học sinh sẽ nhận ra đặc điểm đó. Chọn C.
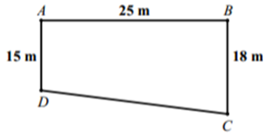
Một phần sân trường được định vị bởi các điểm A,B,C,D như hình vẽ.
Bước đầu chúng được lấy "thăng bằng" đế có cùng độ cao, biết ABCD là hình thang vuông ở A và B với độ dài AB=25m,AD=15m,BC=18m. Do yêu cầu kĩ thuật, khi lát phẳng phần sân trường phải thoát nước về góc sân ở C nên người ta lấy độ cao ở các điểm B,C,D xuống thấp hơn so với độ cao ở A là 10cm,acm,6cm tương ứng. Giá trị của a là số nào sau đây?
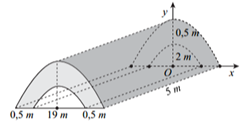
Trong chương trình nông thôn mới, tại một xã Y có xây một cây cầu bằng bê tông như hình vẽ. Tính thể tích (đơn vị m3) khối bê tông để đổ đủ cây cầu. (đường cong trong hình vẽ là các đường parabol)?
Cho các cân bằng hóa học sau:
(1) N2 (g)+ 3H2 (g)⇌2NH3 (g)(2) 2SO2 (g)+ O2 (g)⇌2SO3 (g)(3) CO2 (g)+ H2 (g)⇌CO(g)+ H2O (g)(4) N2O4 (g)⇌2NO2 (g)(5) C (s)+ CO2 (g)⇌2CO (g)
Số cân bằng chuyển dịch theo chiều thuận khi tăng áp suất của hệ phản ứng là
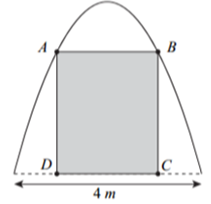
Cho phương trình cos5x=3m−5. Gọi đoạn [a;b] là tập hợp tất cả các giá trị của m để phương trình có nghiệm. Giá trị 3a+b bằng

Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G(x)=0,035x2(15−x),trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng miligam). Liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất là
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10;10] để hàm số y=1mlog23x−4log3x+m+3 xác định trên khoảng (0;+∞)?
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Đối với tôi văn chương không phải là cách đem đến cho người đọc sự thoát li hay sự quên; trái lại văn chương là một thứ khí giới thanh cao và đắc lực mà chúng ta có, để vừa tôn vinh và thay đổi một cái thế giới giả dối, tàn ác, vừa làm cho lòng người đọc thêm trong sạch và phong phú hơn…
Xét hàm số f(x)=|x2+ax+b|, với a,b là tham số. Với M là giá trị lớn nhất của hàm số trên [−1;3]. Khi M nhận giá trị nhỏ nhất có thể được thì a+2b bằng
Hình chóp tam giác đều S.ABC có cạnh đáy là a và mặt bên tạo với đáy góc 45∘. Thể tích khối chóp S.ABC theo a là
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thong thả, dân gian nghỉ việc đồng,
Lúa thì con gái mượt như nhung
Đầy vườn hoa bưởi hoa cam rụng,
Ngào ngạt hương bay, bướm vē vòng.
(Nguyễn Bính, Xuân về, Ngữ văn 10 bộ Chân trời sáng tạo, tập hai,
NXB Giáo dục Việt Nam, 2022)
Các biện pháp tu từ nào được sử dụng trong câu thơ in đậm?